3067:
1422:
3062:{\displaystyle {\begin{aligned}a_{k}&={\frac {f^{(k)}(a)}{k!}}\\&={\frac {1}{2\pi i}}\int _{\partial D}{\frac {f(\zeta )d\zeta }{(\zeta -a)^{k+1}}}\\&={\frac {1}{2\pi i}}\int _{\partial D}{\frac {\sum _{n=0}^{\infty }(-1)^{n}(\zeta -1)^{n}d\zeta }{(\zeta -a)^{k+1}}}\\&={\frac {1}{2\pi i}}\sum _{n=0}^{\infty }(-1)^{n}\int _{\partial D}{\frac {(\zeta -1)^{n}d\zeta }{(\zeta -a)^{k+1}}}\\&={\frac {1}{2\pi i}}\sum _{n=0}^{\infty }(-1)^{n}\int _{0}^{2\pi }{\frac {(a+re^{i\theta }-1)^{n}rie^{i\theta }d\theta }{(re^{i\theta })^{k+1}}}\\&={\frac {1}{2\pi }}\sum _{n=0}^{\infty }(-1)^{n}\int _{0}^{2\pi }{\frac {(a-1+re^{i\theta })^{n}d\theta }{(re^{i\theta })^{k}}}\\&={\frac {1}{2\pi }}\sum _{n=0}^{\infty }(-1)^{n}\int _{0}^{2\pi }{\frac {\sum _{m=0}^{n}{\binom {n}{m}}(a-1)^{n-m}(re^{i\theta })^{m}d\theta }{(re^{i\theta })^{k}}}\\&={\frac {1}{2\pi }}\sum _{n=0}^{\infty }(-1)^{n}\sum _{m=0}^{n}{\binom {n}{m}}(a-1)^{n-m}r^{m-k}\int _{0}^{2\pi }e^{i(m-k)\theta }d\theta \\&={\frac {1}{2\pi }}\sum _{n=k}^{\infty }(-1)^{n}{\binom {n}{k}}(a-1)^{n-k}\int _{0}^{2\pi }d\theta \\&=\sum _{n=k}^{\infty }(-1)^{n}{\binom {n}{k}}(a-1)^{n-k}\\&=(-1)^{k}\sum _{m=0}^{\infty }{\binom {m+k}{k}}(1-a)^{m}\\&=(-1)^{k}a^{-k-1}\end{aligned}}.}
532:
3583:
83:
3205:
7940:
3578:{\displaystyle {\begin{aligned}f(z)&=\sum _{k=0}^{\infty }a_{k}(z-a)^{k}\\&=\sum _{k=0}^{\infty }(-1)^{k}a^{-k-1}(z-a)^{k}\\&={\frac {1}{a}}\sum _{k=0}^{\infty }\left(1-{\frac {z}{a}}\right)^{k}\\&={\frac {1}{a}}{\frac {1}{1-\left(1-{\frac {z}{a}}\right)}}\\&={\frac {1}{z}}\\&={\frac {1}{(z+a)-a}}\end{aligned}}}
5357:
The uniqueness theorem for analytic functions also extends to sheaves of analytic functions: if the sheaf of an analytic function contains the zero germ (i.e., the sheaf is uniformly zero in some neighborhood) then the entire sheaf is zero. Armed with this result, we can see that if we take any germ
6136:
7686:
5342:
7032:
7443:
61:
The step-wise continuation technique may, however, come up against difficulties. These may have an essentially topological nature, leading to inconsistencies (defining more than one value). They may alternatively have to do with the presence of
6392:
3198:
6006:
8662:
4789:
5197:
6590:
5852:
6811:
4352:
8427:
8545:
4122:
4253:
5998:
4984:
694:
7935:{\displaystyle \forall z\in {\mathcal {R}}_{c,n},\qquad {\mathcal {L}}_{c}(z)=\sum _{i=0}^{c^{n}-1}z^{c^{i}}+{\mathcal {L}}_{c}(z^{c^{n}})=\sum _{i=0}^{c^{n}-1}z^{c^{i}}+{\mathcal {L}}_{c}(1)=+\infty .}
1028:
8352:
5599:
5450:
is analytic, and classify the points of the boundary of the domain as regular or singular: the domain boundary is then a natural boundary if all points are singular, in which case the domain is a
3210:
1427:
5219:
235:
8132:
7993:
7528:
3967:
1413:
6885:
3810:
381:
7345:
831:
8181:
8094:
7642:
7278:
7211:
7105:
6877:
6685:
6645:
4837:
8054:
4572:
1263:
5723:
866:
6165:
774:
4003:
are the same when the successive centers have a positive imaginary part or a negative imaginary part. This is not always the case; in particular this is not the case for the
1295:
5076:
5048:
5024:
4896:
4865:
4667:
4496:
6291:
7468:
6296:
5641:
5497:
3844:
3082:
158:
129:
7602:
427:
1378:
1209:
7145:
5884:
5670:
7678:
6725:
3697:
912:
474:
A common way to define functions in complex analysis proceeds by first specifying the function on a small domain only, and then extending it by analytic continuation.
7337:
7171:
6837:
6481:
3890:
1143:
6418:
4636:
3661:
938:
7555:
7311:
7238:
4001:
1057:
6447:
6256:
6223:
6194:
5939:
5910:
5752:
5530:
5390:
for analytic functions, we could construct a wide variety of inverses for the exponential map, but we would discover that they are all represented by some germ in
7065:
3615:
595:
3930:
3910:
3864:
3757:
3737:
3717:
3635:
1355:
1335:
1315:
1186:
1163:
1117:
1097:
1077:
720:
565:
6293:. As a remark, this fact can be problematic if we are performing a complex contour integral over an interval whose real parts are symmetric about zero, say
6131:{\displaystyle \operatorname {Sing} _{P}:=\left\{k^{-1}:k\in \mathbb {Z} ^{+}\right\}=\left\{1,{\frac {1}{2}},{\frac {1}{3}},{\frac {1}{4}},\ldots \right\}}
8565:
7240:-th roots of unity. Hence, since the set formed by all such roots is dense on the boundary of the unit circle, there is no analytic continuation of
4618:
on germs (but not an ordering). This extension by transitivity is one definition of analytic continuation. The equivalence relation will be denoted
4679:
602:
5093:
6497:
945:
5764:
67:
6730:
4273:
70:
is rather different, since singularities then need not be isolated points, and its investigation was a major reason for the development of
8363:
8458:
4035:
1416:
8266:
4160:
5944:
4267:
is ∞. Also note that it would be equivalent to begin with an analytic function defined on some small open set. We say that the vector
520:
4907:
8700:
8695:
8277:
8869:
8199:
5538:
8829:
8822:
5337:{\displaystyle g=\left(1,0,1,-{\frac {1}{2}},{\frac {1}{3}},-{\frac {1}{4}},{\frac {1}{5}},-{\frac {1}{6}},\ldots \right)}
5427:
inside that disc. Consider points on the circle of convergence. A point for which there is a neighbourhood on which
699:
50:. Analytic continuation often succeeds in defining further values of a function, for example in a new region where the
8864:
8817:
180:
8099:
500:. The idea of finding the maximal analytic continuation of a function in turn led to the development of the idea of
7952:
63:
7473:
3935:
516:
249:
7027:{\displaystyle {\mathcal {L}}_{c}(z)=\sum _{i=0}^{m-1}z^{c^{i}}+{\mathcal {L}}_{c}(z^{c^{m}}),\forall |z|<1.}
8874:
7438:{\displaystyle {\mathcal {R}}_{c,n}:=\left\{z\in \mathbb {D} \cup \partial {\mathbb {D} }:z^{c^{n}}=1\right\},}
5387:
1383:
512:
3762:
310:
779:
8812:
8158:
8059:
7607:
7243:
7176:
7070:
6842:
6650:
8437:
6598:
4812:
7998:
5755:
5605:
5403:
4521:
1214:
482:
82:
5687:
836:
6144:
725:
8733:
8134:
Hence, there is no analytic continuation for these functions beyond the interior of the unit circle.
6387:{\displaystyle I_{F}\subseteq \mathbb {C} \ {\text{such that}}\ \Re (s)\in (-C,C),\forall s\in I_{F}}
5452:
4615:
1268:
463:
43:
5057:
5029:
5005:
4877:
4846:
4648:
4477:
8690:
6261:
5500:
5408:
5348:
4900:
4611:
4026:
508:
478:
7451:
5611:
5467:
3817:
141:
112:
7567:
5211:
4607:
4515:
4359:
4132:
4021:
392:
4259:
Note that without loss of generality, here and below, we will always assume that a maximal such
1360:
1191:
7114:
5860:
5646:
8837:
8433:
8143:
7647:
6694:
5203:
4004:
3666:
874:
531:
497:
95:
47:
7316:
7150:
6816:
6460:
3869:
1122:
8741:
8196:
7945:
Thus for any arc on the boundary of the unit circle, there are an infinite number of points
6397:
4999:
4995:
4840:
4621:
3640:
3076:
917:
459:
71:
55:
31:
7533:
7290:
7216:
3974:
3866:, and determine where the new power series converges. If the region contains points not in
1035:
8840:
6484:
6423:
6232:
6199:
6170:
5915:
5889:
5728:
5677:
5506:
5051:
4871:
501:
493:
51:
8441:
7044:
4606:. This compatibility condition is neither transitive, symmetric nor antisymmetric. If we
3590:
574:
8737:
481:
on the small domain and then using this equation to extend the domain. Examples are the
17:
7558:
4008:
3915:
3895:
3849:
3742:
3722:
3702:
3620:
1340:
1320:
1300:
1171:
1148:
1102:
1082:
1062:
705:
550:
486:
8152:(i.e., an extension of an analytic function to an analytic function on a bigger set).
6453:
Example II: A typical lacunary series (natural boundary as subsets of the unit circle)
8858:
5673:
4590:
specify identical functions on the intersection of the two domains, then we say that
3193:{\displaystyle {\frac {1}{(1-x)^{k+1}}}=\sum _{m=0}^{\infty }{\binom {m+k}{k}}x^{m}.}
272:
106:
8763:
8721:
8798:
The Taylor series: an introduction to the theory of functions of a complex variable
8775:
4128:
568:
496:
was first developed to define a natural domain for the analytic continuation of an
8657:{\displaystyle f(z)=\sum _{k=0}^{\infty }\varepsilon _{k}\alpha _{k}(z-z_{0})^{k}}
7287:
The proof of this fact is generalized from a standard argument for the case where
5446:
More generally, we may apply the definition to any open connected domain on which
4025:. The general theory of analytic continuation and its generalizations is known as
4463:, ...) is a germ if it represents a power series of an analytic function around
35:
8432:
the circle of convergence is a natural boundary. Such a power series is called
5460:
Example I: A function with a natural boundary at zero (the prime zeta function)
5366:
of the logarithm function, as described above, and turn it into a power series
8745:
8845:
4784:{\displaystyle U_{r}(g)=\{h\in {\mathcal {G}}:g\geq h,|g_{0}-h_{0}|<r\}.}
458:
and hence must vanish on its entire domain. This follows directly from the
8148:
The monodromy theorem gives a sufficient condition for the existence of a
5192:{\displaystyle L(z)=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}}{k}}(z-1)^{k}}
6585:{\displaystyle {\mathcal {L}}_{c}(z):=\sum _{n\geq 1}z^{c^{n}},|z|<1.}
4642:
99:
5847:{\displaystyle P(s)=\sum _{n\geq 1}\mu (n){\frac {\log \zeta (ns)}{n}}.}
1059:'s and determine whether this new power series converges in an open set
477:
In practice, this continuation is often done by first establishing some
8436:. This theorem has been substantially generalized by Eugen Fabry (see
7604:. Now the key part of the proof is to use the functional equation for
5680:. The prime zeta function has an analytic continuation to all complex
6806:{\displaystyle {\mathcal {L}}_{c}(z)=z^{c}+{\mathcal {L}}_{c}(z^{c})}
6420:, where the integrand is a function with denominator that depends on
4347:{\displaystyle g=(z_{0},\alpha _{0},\alpha _{1},\alpha _{2},\ldots )}
450:
is an analytic function which vanishes on the open, connected domain
8422:{\displaystyle \liminf _{k\to \infty }{\frac {n_{k+1}}{n_{k}}}>1}
3932:
can be analytically continued to the whole punctured complex plane
8540:{\displaystyle f(z)=\sum _{k=0}^{\infty }\alpha _{k}(z-z_{0})^{k}}
6229:
left of (or at) zero, i.e., there is no continuation possible for
5354:
corresponding to it. This is the sheaf of the logarithm function.
4117:{\displaystyle f(z)=\sum _{k=0}^{\infty }\alpha _{k}(z-z_{0})^{k}}
530:
81:
4248:{\displaystyle D_{r}(z_{0})=\{z\in \mathbb {C} :|z-z_{0}|<r\}}
914:, and focus on recentering the power series at a different point
5993:{\displaystyle s:={\tfrac {1}{k}},\forall k\in \mathbb {Z} ^{+}}
8681:
The proof of this theorem makes use of
Hadamard's gap theorem.
5401:
In older literature, sheaves of analytic functions were called
4019:
The power series defined below is generalized by the idea of a
5347:
This germ has a radius of convergence of 1, and so there is a
4614:, we obtain a symmetric relation, which is therefore also an
267:
Analytic continuations are unique in the following sense: if
27:
Extension of the domain of an analytic function (mathematics)
8066:
7959:
7900:
7806:
7726:
7702:
7614:
7485:
7352:
7250:
7183:
7077:
6965:
6892:
6849:
6776:
6737:
6657:
6504:
5063:
5035:
5011:
4979:{\displaystyle \phi _{g}(h)=h_{0}:U_{r}(g)\to \mathbb {C} ,}
4883:
4852:
4824:
4716:
4654:
4483:
689:{\displaystyle f(z)=\sum _{k=0}^{\infty }(-1)^{k}(z-1)^{k}.}
54:
representation which initially defined the function becomes
4474:> 0. Therefore, we can safely speak of the set of germs
86:
Analytic continuation of natural logarithm (imaginary part)
7995:. This condition is equivalent to saying that the circle
1023:{\displaystyle f(z)=\sum _{k=0}^{\infty }a_{k}(z-a)^{k}.}
8347:{\displaystyle f(z)=\sum _{k=0}^{\infty }a_{k}z^{n_{k}}}
5604:
This function is analogous to the summatory form of the
7067:. We consider the question of analytic continuation of
6813:. It is also not difficult to see that for any integer
6141:
has accumulation point 0 (the limit of the sequence as
5594:{\displaystyle P(s):=\sum _{p\ {\text{ prime}}}p^{-s}.}
5955:
5419:
Suppose that a power series has radius of convergence
3773:
8568:
8461:
8366:
8280:
8161:
8102:
8062:
8001:
7955:
7689:
7650:
7610:
7570:
7536:
7476:
7454:
7348:
7319:
7293:
7246:
7219:
7179:
7153:
7117:
7073:
7047:
6888:
6845:
6819:
6733:
6697:
6653:
6601:
6500:
6463:
6426:
6400:
6299:
6264:
6235:
6202:
6173:
6167:), we can see that zero forms a natural boundary for
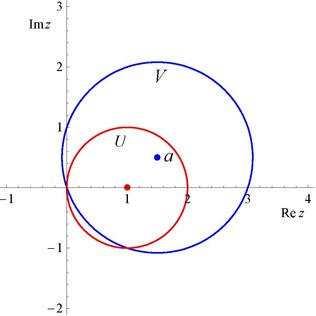
6147:
6009:
5947:
5918:
5892:
5863:
5767:
5731:
5690:
5649:
5614:
5541:
5509:
5470:
5374:) then this function will have the property that exp(
5222:
5096:
5060:
5032:
5008:
4910:
4880:
4849:
4815:
4682:
4651:
4624:
4524:
4480:
4276:
4163:
4038:
3977:
3938:
3918:
3898:
3872:
3852:
3820:
3765:
3745:
3725:
3705:
3669:
3643:
3623:
3593:
3208:
3085:
1425:
1386:
1363:
1343:
1323:
1303:
1271:
1217:
1194:
1174:
1151:
1125:
1105:
1085:
1065:
1038:
948:
920:
877:
839:
782:
728:
708:
605:
577:
553:
395:
313:
183:
144:
115:
7470:
denotes the open unit disk in the complex plane and
5643:in so much as it is the same summatory function as
8656:
8539:
8421:
8346:
8175:
8126:
8088:
8048:
7987:
7934:
7672:
7636:
7596:
7549:
7522:
7462:
7437:
7331:
7305:
7272:
7232:
7205:
7165:
7139:
7099:
7059:
7026:
6871:
6831:
6805:
6719:
6679:
6639:
6584:
6475:
6441:
6412:
6386:
6285:
6250:
6217:
6188:
6159:
6130:
5992:
5933:
5904:
5878:
5846:
5746:
5717:
5664:
5635:
5593:
5524:
5491:
5398:is the "one true inverse" of the exponential map.
5336:
5191:
5070:
5042:
5018:
4978:
4890:
4859:
4831:
4783:
4661:
4630:
4566:
4490:
4346:
4247:
4116:
3995:
3961:
3924:
3904:
3884:
3858:
3838:
3804:
3751:
3731:
3711:
3691:
3655:
3629:
3609:
3577:
3192:
3061:
1407:
1372:
1349:
1329:
1309:
1289:
1257:
1203:
1180:
1157:
1137:
1111:
1091:
1071:
1051:
1022:
932:
906:
860:
825:
768:
714:
688:
589:
559:
421:
375:
229:
152:
123:
8210:has an analytic continuation along every path in
3171:
3150:
2976:
2955:
2868:
2855:
2744:
2731:
2561:
2548:
8368:
7564:that lie on or inside the unit circle such that
3971:In this particular case the obtained values of
230:{\displaystyle F(z)=f(z)\qquad \forall z\in U,}
8127:{\displaystyle c\in \mathbb {Z} \quad c>1.}
5725:, a fact which follows from the expression of
8782:(3 ed.). McGraw-Hill. pp. 172, 284.
8241:is a sheaf whose set of base points contains
7988:{\displaystyle {\mathcal {L}}_{c}(z)=\infty }
5672:, except with indices restricted only to the
2356:
2343:
1099:. If so, we will have analytically continued
8:
8043:
8015:
7523:{\displaystyle |{\mathcal {R}}_{c,n}|=c^{n}}
5676:instead of taking the sum over all positive
5386:. If we had decided to use a version of the
5210:= 1. This power series can be turned into a
4775:
4705:
4242:
4193:
3962:{\displaystyle \mathbb {C} \setminus \{0\}.}
3953:
3947:
820:
792:
763:
735:
515:. For example, the analytic continuation of
8722:"Maximal Extension of Schwarzschild Metric"
7041:, the lacunary series function diverges at
3892:, then we will have analytically continued
1419:to calculate the new coefficients, one has
702:, its radius of convergence is 1. That is,
8056:forms a natural boundary for the function
6839:, we have another functional equation for
547:Begin with a particular analytic function
8648:
8638:
8619:
8609:
8599:
8588:
8567:
8531:
8521:
8502:
8492:
8481:
8460:
8405:
8389:
8383:
8371:
8365:
8336:
8331:
8321:
8311:
8300:
8279:
8245:, then there exists an analytic function
8233:In the above language this means that if
8169:
8168:
8160:
8110:
8109:
8101:
8071:
8065:
8064:
8061:
8032:
8024:
8006:
8000:
7964:
7958:
7957:
7954:
7905:
7899:
7898:
7886:
7881:
7863:
7858:
7847:
7829:
7824:
7811:
7805:
7804:
7792:
7787:
7769:
7764:
7753:
7731:
7725:
7724:
7707:
7701:
7700:
7688:
7659:
7651:
7649:
7619:
7613:
7612:
7609:
7580:
7575:
7569:
7541:
7535:
7514:
7502:
7490:
7484:
7483:
7477:
7475:
7456:
7455:
7453:
7413:
7408:
7396:
7395:
7394:
7384:
7383:
7357:
7351:
7350:
7347:
7318:
7292:
7255:
7249:
7248:
7245:
7224:
7218:
7188:
7182:
7181:
7178:
7152:
7126:
7118:
7116:
7082:
7076:
7075:
7072:
7046:
7013:
7005:
6988:
6983:
6970:
6964:
6963:
6951:
6946:
6930:
6919:
6897:
6891:
6890:
6887:
6854:
6848:
6847:
6844:
6818:
6794:
6781:
6775:
6774:
6764:
6742:
6736:
6735:
6732:
6706:
6698:
6696:
6662:
6656:
6655:
6652:
6631:
6606:
6600:
6571:
6563:
6552:
6547:
6531:
6509:
6503:
6502:
6499:
6462:
6425:
6399:
6378:
6321:
6314:
6313:
6304:
6298:
6263:
6234:
6201:
6172:
6146:
6107:
6094:
6081:
6056:
6052:
6051:
6032:
6014:
6008:
5984:
5980:
5979:
5954:
5946:
5917:
5891:
5862:
5811:
5787:
5766:
5730:
5689:
5648:
5613:
5579:
5568:
5561:
5540:
5508:
5469:
5313:
5297:
5284:
5268:
5255:
5221:
5183:
5149:
5133:
5127:
5116:
5095:
5062:
5061:
5059:
5034:
5033:
5031:
5010:
5009:
5007:
4969:
4968:
4950:
4937:
4915:
4909:
4898:(i.e., an equivalence class) is called a
4882:
4881:
4879:
4851:
4850:
4848:
4823:
4822:
4814:
4764:
4758:
4745:
4736:
4715:
4714:
4687:
4681:
4653:
4652:
4650:
4623:
4553:
4547:
4534:
4525:
4523:
4482:
4481:
4479:
4329:
4316:
4303:
4290:
4275:
4231:
4225:
4210:
4203:
4202:
4181:
4168:
4162:
4108:
4098:
4079:
4069:
4058:
4037:
3976:
3940:
3939:
3937:
3917:
3897:
3871:
3851:
3819:
3772:
3764:
3744:
3724:
3704:
3678:
3670:
3668:
3642:
3622:
3602:
3594:
3592:
3541:
3521:
3493:
3470:
3460:
3444:
3429:
3411:
3400:
3386:
3370:
3339:
3329:
3310:
3299:
3279:
3257:
3247:
3236:
3209:
3207:
3181:
3170:
3149:
3147:
3141:
3130:
3108:
3086:
3084:
3037:
3027:
2998:
2975:
2954:
2952:
2946:
2935:
2925:
2890:
2867:
2854:
2852:
2846:
2827:
2816:
2787:
2782:
2766:
2743:
2730:
2728:
2722:
2703:
2692:
2673:
2633:
2620:
2615:
2599:
2583:
2560:
2547:
2545:
2539:
2528:
2518:
2499:
2488:
2469:
2450:
2437:
2413:
2400:
2378:
2355:
2342:
2340:
2334:
2323:
2316:
2307:
2302:
2292:
2273:
2262:
2243:
2224:
2211:
2187:
2174:
2149:
2140:
2135:
2125:
2106:
2095:
2076:
2051:
2038:
2011:
1995:
1976:
1957:
1948:
1943:
1933:
1914:
1903:
1881:
1856:
1826:
1807:
1798:
1788:
1769:
1758:
1736:
1711:
1681:
1659:
1640:
1629:
1622:
1613:
1591:
1566:
1527:
1518:
1496:
1454:
1447:
1434:
1426:
1424:
1408:{\displaystyle D\cup \partial D\subset U}
1385:
1362:
1342:
1322:
1302:
1270:
1244:
1230:
1216:
1193:
1173:
1150:
1124:
1104:
1084:
1064:
1043:
1037:
1011:
989:
979:
968:
947:
919:
896:
876:
838:
809:
795:
781:
752:
738:
727:
707:
677:
655:
636:
625:
604:
576:
552:
413:
400:
394:
340:
318:
312:
182:
146:
145:
143:
117:
116:
114:
722:is defined and analytic on the open set
8712:
5202:is a power series corresponding to the
4904:. We also note that the map defined by
3944:
3805:{\displaystyle a={\tfrac {1}{2}}(3+i).}
376:{\displaystyle F_{1}(z)=F_{2}(z)=f(z),}
8226:has a direct analytic continuation to
826:{\displaystyle \partial U=\{|z-1|=1\}}
244:is called an analytic continuation of
8176:{\displaystyle D\subset \mathbb {C} }
8089:{\displaystyle {\mathcal {L}}_{c}(z)}
7637:{\displaystyle {\mathcal {L}}_{c}(z)}
7273:{\displaystyle {\mathcal {L}}_{c}(z)}
7206:{\displaystyle {\mathcal {L}}_{c}(z)}
7100:{\displaystyle {\mathcal {L}}_{c}(z)}
6872:{\displaystyle {\mathcal {L}}_{c}(z)}
6680:{\displaystyle {\mathcal {L}}_{c}(z)}
4594:is generated by (or compatible with)
7:
8800:. New York: Dover Publications, Inc.
8550:be a power series, then there exist
6640:{\displaystyle c^{n+1}=c\cdot c^{n}}
5886:has a simple, non-removable pole at
3814:We can continue the process: select
3739:and is actually larger in area than
3071:The last summation results from the
6647:there is a functional equation for
4832:{\displaystyle g\in {\mathcal {G}}}
4582:and if the power series defined by
170:is an analytic function defined on
8600:
8493:
8378:
8312:
8237:is a simply connected domain, and
8049:{\displaystyle C_{1}:=\{z:|z|=1\}}
7982:
7926:
7690:
7391:
7002:
6365:
6329:
6271:
6154:
5969:
5697:
5615:
5471:
5128:
4998:. The set of such charts forms an
4567:{\displaystyle |h_{0}-g_{0}|<r}
4070:
3412:
3311:
3248:
3154:
3142:
2959:
2947:
2859:
2828:
2735:
2704:
2552:
2500:
2347:
2274:
2107:
1915:
1799:
1770:
1641:
1614:
1519:
1393:
1364:
1258:{\displaystyle \rho =1-|a-1|>0}
1195:
980:
852:
783:
637:
212:
25:
8214:, starting from some fixed point
7037:For any positive natural numbers
6225:has no analytic continuation for
5718:{\displaystyle 0<\Re (s)<1}
5423:and defines an analytic function
5086:Examples of analytic continuation
861:{\displaystyle z=0\in \partial U}
833:. Indeed, the series diverges at
567:. In this case, it is given by a
507:Analytic continuation is used in
275:domain of two analytic functions
6160:{\displaystyle k\mapsto \infty }
5443:if all its points are singular.
4990:is the radius of convergence of
4578:is the radius of convergence of
4502:The topology of the set of germs
4470:with some radius of convergence
3759:. The plot shows the result for
3587:which has radius of convergence
1417:Cauchy's differentiation formula
769:{\displaystyle U=\{|z-1|<1\}}
8701:Numerical analytic continuation
8696:Holomorphic functional calculus
8114:
7722:
3846:, recenter the power series at
1290:{\displaystyle 0<r<\rho }
211:
8645:
8625:
8578:
8572:
8528:
8508:
8471:
8465:
8375:
8290:
8284:
8267:Ostrowski–Hadamard gap theorem
8083:
8077:
8033:
8025:
7976:
7970:
7917:
7911:
7837:
7817:
7743:
7737:
7660:
7652:
7631:
7625:
7503:
7478:
7267:
7261:
7200:
7194:
7127:
7119:
7094:
7088:
7014:
7006:
6996:
6976:
6909:
6903:
6866:
6860:
6800:
6787:
6754:
6748:
6707:
6699:
6674:
6668:
6572:
6564:
6521:
6515:
6491:by the power series expansion
6436:
6430:
6359:
6344:
6338:
6332:
6280:
6274:
6245:
6239:
6212:
6206:
6183:
6177:
6151:
5928:
5922:
5873:
5867:
5832:
5823:
5808:
5802:
5777:
5771:
5741:
5735:
5706:
5700:
5659:
5653:
5624:
5618:
5551:
5545:
5519:
5513:
5480:
5474:
5180:
5167:
5146:
5136:
5106:
5100:
5071:{\displaystyle {\mathcal {G}}}
5043:{\displaystyle {\mathcal {G}}}
5019:{\displaystyle {\mathcal {G}}}
4965:
4962:
4956:
4927:
4921:
4891:{\displaystyle {\mathcal {G}}}
4860:{\displaystyle {\mathcal {G}}}
4765:
4737:
4699:
4693:
4662:{\displaystyle {\mathcal {G}}}
4554:
4526:
4491:{\displaystyle {\mathcal {G}}}
4341:
4283:
4232:
4211:
4187:
4174:
4105:
4085:
4048:
4042:
3990:
3981:
3912:even further. This particular
3796:
3784:
3679:
3671:
3603:
3595:
3559:
3547:
3367:
3354:
3326:
3316:
3276:
3263:
3222:
3216:
3105:
3092:
3024:
3014:
2995:
2982:
2922:
2912:
2887:
2874:
2843:
2833:
2763:
2750:
2719:
2709:
2649:
2637:
2580:
2567:
2515:
2505:
2447:
2427:
2410:
2390:
2375:
2362:
2289:
2279:
2221:
2201:
2184:
2152:
2122:
2112:
2048:
2028:
1992:
1960:
1930:
1920:
1853:
1840:
1823:
1810:
1785:
1775:
1708:
1695:
1678:
1665:
1656:
1646:
1563:
1550:
1539:
1533:
1472:
1466:
1461:
1455:
1245:
1231:
1145:which is strictly larger than
1008:
995:
958:
952:
887:
881:
810:
796:
753:
739:
674:
661:
652:
642:
615:
609:
367:
361:
352:
346:
330:
324:
208:
202:
193:
187:
1:
8758:See the example given on the
8720:Kruskal, M. D. (1960-09-01).
6286:{\displaystyle 0\geq \Re (s)}
5431:has an analytic extension is
42:is a technique to extend the
8667:has the convergence disc of
8150:direct analytic continuation
7463:{\displaystyle \mathbb {D} }
5636:{\displaystyle \Re (s)>1}
5492:{\displaystyle \Re (s)>1}
3839:{\displaystyle b\in U\cup V}
521:Kruskal–Szekeres coordinates
153:{\displaystyle \mathbb {C} }
124:{\displaystyle \mathbb {C} }
8818:Encyclopedia of Mathematics
8260:
7597:{\displaystyle z^{c^{n}}=1}
7284:whose modulus exceeds one.
5912:, it can then be seen that
5080:universal analytic function
4015:Formal definition of a germ
3079:, which gives the formula
871:Pretend we don't know that
535:Analytic continuation from
422:{\displaystyle F_{1}=F_{2}}
137:is a larger open subset of
8891:
8787:Ludwig Bieberbach (1955).
8264:
8141:
7949:within this arc such that
6000:. Since the set of points
1373:{\displaystyle \partial D}
1204:{\displaystyle \partial U}
1079:which is not contained in
7147:As we shall see, for any
7140:{\displaystyle |z|>1.}
5879:{\displaystyle \zeta (s)}
5754:by the logarithms of the
5665:{\displaystyle \zeta (s)}
5411:for the general concept.
4263:was chosen, even if that
517:Schwarzschild coordinates
68:several complex variables
8746:10.1103/PhysRev.119.1743
8187:an analytic function on
8096:for any fixed choice of
7673:{\displaystyle |z|<1}
6720:{\displaystyle |z|<1}
5499:we define the so-called
5388:inverse function theorem
5078:is sometimes called the
3692:{\displaystyle |a|>1}
907:{\displaystyle f(z)=1/z}
18:Meromorphic continuation
8841:"Analytic Continuation"
8813:"Analytic continuation"
8789:Analytische Fortsetzung
8678:as a natural boundary.
8447:
7332:{\displaystyle n\geq 1}
7166:{\displaystyle n\geq 1}
6832:{\displaystyle m\geq 1}
6476:{\displaystyle c\geq 2}
4011:of the above function.
3885:{\displaystyle U\cup V}
1380:be its boundary. Then
1138:{\displaystyle U\cup V}
700:Cauchy–Hadamard theorem
543:(centered at a=(3+i)/2)
98:defined on a non-empty
8658:
8604:
8541:
8497:
8423:
8348:
8316:
8261:Hadamard's gap theorem
8253:whose germs belong to
8177:
8128:
8090:
8050:
7989:
7936:
7876:
7782:
7674:
7638:
7598:
7551:
7524:
7464:
7439:
7333:
7307:
7274:
7234:
7207:
7167:
7141:
7101:
7061:
7028:
6941:
6873:
6833:
6807:
6721:
6681:
6641:
6586:
6477:
6443:
6414:
6413:{\displaystyle C>0}
6388:
6287:
6252:
6219:
6190:
6161:
6132:
5994:
5935:
5906:
5880:
5848:
5748:
5719:
5666:
5637:
5595:
5526:
5493:
5404:multi-valued functions
5338:
5193:
5132:
5072:
5044:
5020:
4980:
4892:
4861:
4833:
4785:
4663:
4632:
4631:{\displaystyle \cong }
4568:
4492:
4348:
4249:
4118:
4074:
3997:
3963:
3926:
3906:
3886:
3860:
3840:
3806:
3753:
3733:
3713:
3693:
3657:
3656:{\displaystyle a\in U}
3631:
3611:
3579:
3416:
3315:
3252:
3194:
3146:
3063:
2951:
2832:
2708:
2544:
2504:
2339:
2278:
2111:
1919:
1774:
1645:
1409:
1374:
1351:
1331:
1317:be the disk of radius
1311:
1291:
1259:
1205:
1182:
1159:
1139:
1113:
1093:
1073:
1053:
1024:
984:
934:
933:{\displaystyle a\in U}
908:
862:
827:
770:
716:
690:
641:
591:
561:
544:
423:
377:
248:. In other words, the
231:
154:
125:
87:
8870:Meromorphic functions
8830:Analytic Continuation
8659:
8584:
8542:
8477:
8424:
8349:
8296:
8178:
8129:
8091:
8051:
7990:
7937:
7843:
7749:
7675:
7639:
7599:
7552:
7550:{\displaystyle c^{n}}
7525:
7465:
7440:
7334:
7313:Namely, for integers
7308:
7306:{\displaystyle c:=2.}
7275:
7235:
7233:{\displaystyle c^{n}}
7208:
7168:
7142:
7102:
7062:
7029:
6915:
6874:
6834:
6808:
6722:
6682:
6642:
6587:
6478:
6449:in an essential way.
6444:
6415:
6389:
6288:
6253:
6220:
6191:
6162:
6133:
5995:
5941:has a simple pole at
5936:
5907:
5881:
5849:
5756:Riemann zeta function
5749:
5720:
5667:
5638:
5606:Riemann zeta function
5596:
5527:
5494:
5339:
5194:
5112:
5073:
5045:
5021:
4981:
4893:
4862:
4834:
4786:
4664:
4633:
4569:
4493:
4349:
4250:
4119:
4054:
3998:
3996:{\displaystyle f(-1)}
3964:
3927:
3907:
3887:
3861:
3841:
3807:
3754:
3734:
3714:
3694:
3658:
3632:
3612:
3580:
3396:
3295:
3232:
3195:
3126:
3075:th derivation of the
3064:
2931:
2812:
2688:
2524:
2484:
2319:
2258:
2091:
1899:
1754:
1625:
1410:
1375:
1352:
1332:
1312:
1292:
1260:
1206:
1183:
1160:
1140:
1114:
1094:
1074:
1054:
1052:{\displaystyle a_{k}}
1025:
964:
935:
909:
863:
828:
771:
717:
691:
621:
592:
562:
534:
483:Riemann zeta function
464:holomorphic functions
424:
378:
232:
155:
126:
85:
40:analytic continuation
8566:
8559:∈ {−1, 1} such that
8459:
8364:
8278:
8159:
8100:
8060:
7999:
7953:
7687:
7648:
7608:
7568:
7534:
7474:
7452:
7346:
7317:
7291:
7244:
7217:
7177:
7151:
7115:
7071:
7045:
6886:
6843:
6817:
6731:
6695:
6651:
6599:
6498:
6461:
6442:{\displaystyle P(s)}
6424:
6398:
6297:
6262:
6251:{\displaystyle P(s)}
6233:
6218:{\displaystyle P(s)}
6200:
6196:. This implies that
6189:{\displaystyle P(s)}
6171:
6145:
6007:
5945:
5934:{\displaystyle P(s)}
5916:
5905:{\displaystyle s:=1}
5890:
5861:
5765:
5747:{\displaystyle P(s)}
5729:
5688:
5647:
5612:
5539:
5525:{\displaystyle P(s)}
5507:
5468:
5453:domain of holomorphy
5220:
5094:
5058:
5030:
5006:
4908:
4878:
4847:
4843:for the topology on
4813:
4680:
4649:
4622:
4616:equivalence relation
4522:
4478:
4274:
4161:
4036:
3975:
3936:
3916:
3896:
3870:
3850:
3818:
3763:
3743:
3723:
3703:
3667:
3641:
3621:
3591:
3206:
3083:
1423:
1384:
1361:
1341:
1321:
1301:
1269:
1215:
1192:
1172:
1149:
1123:
1103:
1083:
1063:
1036:
1032:We'll calculate the
946:
918:
875:
837:
780:
726:
706:
603:
575:
551:
513:Einstein's equations
509:Riemannian manifolds
393:
311:
181:
142:
113:
44:domain of definition
8738:1960PhRv..119.1743K
8691:Mittag-Leffler star
8438:Fabry's gap theorem
8271:For a power series
8183:is an open set and
7060:{\displaystyle z=1}
5501:prime zeta function
5439:. The circle is a
4872:connected component
4154:> 0, defined by
3719:is not a subset of
3610:{\displaystyle |a|}
2795:
2628:
2315:
2148:
1956:
776:which has boundary
590:{\displaystyle z=1}
539:(centered at 1) to
479:functional equation
8865:Analytic functions
8838:Weisstein, Eric W.
8796:P. Dienes (1957).
8791:. Springer-Verlag.
8654:
8537:
8419:
8382:
8344:
8173:
8124:
8086:
8046:
7985:
7932:
7670:
7634:
7594:
7547:
7530:, i.e., there are
7520:
7460:
7435:
7329:
7303:
7270:
7230:
7203:
7163:
7137:
7097:
7057:
7024:
6869:
6829:
6803:
6717:
6677:
6637:
6582:
6542:
6473:
6439:
6410:
6384:
6283:
6248:
6215:
6186:
6157:
6128:
5990:
5964:
5931:
5902:
5876:
5844:
5798:
5744:
5715:
5662:
5633:
5591:
5574:
5522:
5489:
5334:
5189:
5068:
5040:
5016:
4976:
4888:
4857:
4841:basis of open sets
4829:
4781:
4659:
4628:
4564:
4488:
4344:
4245:
4131:converging in the
4114:
3993:
3959:
3922:
3902:
3882:
3856:
3836:
3802:
3782:
3749:
3729:
3709:
3689:
3653:
3627:
3607:
3575:
3573:
3190:
3059:
3054:
2778:
2611:
2298:
2131:
1939:
1405:
1370:
1347:
1327:
1307:
1287:
1255:
1201:
1178:
1168:The distance from
1155:
1135:
1109:
1089:
1069:
1049:
1020:
930:
904:
858:
823:
766:
712:
686:
587:
557:
545:
436:. This is because
419:
373:
227:
150:
121:
88:
78:Initial discussion
8411:
8367:
8144:Monodromy theorem
8138:Monodromy theorem
7107:to other complex
6527:
6328:
6324:
6320:
6115:
6102:
6089:
5963:
5839:
5783:
5571:
5567:
5557:
5394:. In that sense,
5321:
5305:
5292:
5276:
5263:
5204:natural logarithm
5165:
4005:complex logarithm
3925:{\displaystyle f}
3905:{\displaystyle f}
3859:{\displaystyle b}
3781:
3752:{\displaystyle U}
3732:{\displaystyle U}
3712:{\displaystyle V}
3630:{\displaystyle 0}
3569:
3529:
3509:
3501:
3468:
3437:
3394:
3169:
3121:
2974:
2866:
2742:
2686:
2559:
2482:
2457:
2354:
2256:
2231:
2089:
2064:
1897:
1869:
1752:
1724:
1607:
1579:
1512:
1484:
1350:{\displaystyle a}
1330:{\displaystyle r}
1310:{\displaystyle D}
1181:{\displaystyle a}
1158:{\displaystyle U}
1112:{\displaystyle f}
1092:{\displaystyle U}
1072:{\displaystyle V}
715:{\displaystyle f}
560:{\displaystyle f}
498:analytic function
492:The concept of a
264:we started with.
96:analytic function
48:analytic function
16:(Redirected from
8882:
8851:
8850:
8826:
8801:
8792:
8783:
8780:Complex Analysis
8767:
8764:natural boundary
8756:
8750:
8749:
8732:(5): 1743–1745.
8717:
8663:
8661:
8660:
8655:
8653:
8652:
8643:
8642:
8624:
8623:
8614:
8613:
8603:
8598:
8546:
8544:
8543:
8538:
8536:
8535:
8526:
8525:
8507:
8506:
8496:
8491:
8428:
8426:
8425:
8420:
8412:
8410:
8409:
8400:
8399:
8384:
8381:
8353:
8351:
8350:
8345:
8343:
8342:
8341:
8340:
8326:
8325:
8315:
8310:
8197:simply connected
8182:
8180:
8179:
8174:
8172:
8133:
8131:
8130:
8125:
8113:
8095:
8093:
8092:
8087:
8076:
8075:
8070:
8069:
8055:
8053:
8052:
8047:
8036:
8028:
8011:
8010:
7994:
7992:
7991:
7986:
7969:
7968:
7963:
7962:
7941:
7939:
7938:
7933:
7910:
7909:
7904:
7903:
7893:
7892:
7891:
7890:
7875:
7868:
7867:
7857:
7836:
7835:
7834:
7833:
7816:
7815:
7810:
7809:
7799:
7798:
7797:
7796:
7781:
7774:
7773:
7763:
7736:
7735:
7730:
7729:
7718:
7717:
7706:
7705:
7679:
7677:
7676:
7671:
7663:
7655:
7643:
7641:
7640:
7635:
7624:
7623:
7618:
7617:
7603:
7601:
7600:
7595:
7587:
7586:
7585:
7584:
7556:
7554:
7553:
7548:
7546:
7545:
7529:
7527:
7526:
7521:
7519:
7518:
7506:
7501:
7500:
7489:
7488:
7481:
7469:
7467:
7466:
7461:
7459:
7444:
7442:
7441:
7436:
7431:
7427:
7420:
7419:
7418:
7417:
7400:
7399:
7387:
7368:
7367:
7356:
7355:
7338:
7336:
7335:
7330:
7312:
7310:
7309:
7304:
7279:
7277:
7276:
7271:
7260:
7259:
7254:
7253:
7239:
7237:
7236:
7231:
7229:
7228:
7213:diverges at the
7212:
7210:
7209:
7204:
7193:
7192:
7187:
7186:
7172:
7170:
7169:
7164:
7146:
7144:
7143:
7138:
7130:
7122:
7106:
7104:
7103:
7098:
7087:
7086:
7081:
7080:
7066:
7064:
7063:
7058:
7033:
7031:
7030:
7025:
7017:
7009:
6995:
6994:
6993:
6992:
6975:
6974:
6969:
6968:
6958:
6957:
6956:
6955:
6940:
6929:
6902:
6901:
6896:
6895:
6878:
6876:
6875:
6870:
6859:
6858:
6853:
6852:
6838:
6836:
6835:
6830:
6812:
6810:
6809:
6804:
6799:
6798:
6786:
6785:
6780:
6779:
6769:
6768:
6747:
6746:
6741:
6740:
6726:
6724:
6723:
6718:
6710:
6702:
6686:
6684:
6683:
6678:
6667:
6666:
6661:
6660:
6646:
6644:
6643:
6638:
6636:
6635:
6617:
6616:
6591:
6589:
6588:
6583:
6575:
6567:
6559:
6558:
6557:
6556:
6541:
6514:
6513:
6508:
6507:
6483:, we define the
6482:
6480:
6479:
6474:
6448:
6446:
6445:
6440:
6419:
6417:
6416:
6411:
6393:
6391:
6390:
6385:
6383:
6382:
6326:
6325:
6322:
6318:
6317:
6309:
6308:
6292:
6290:
6289:
6284:
6257:
6255:
6254:
6249:
6224:
6222:
6221:
6216:
6195:
6193:
6192:
6187:
6166:
6164:
6163:
6158:
6137:
6135:
6134:
6129:
6127:
6123:
6116:
6108:
6103:
6095:
6090:
6082:
6066:
6062:
6061:
6060:
6055:
6040:
6039:
6019:
6018:
5999:
5997:
5996:
5991:
5989:
5988:
5983:
5965:
5956:
5940:
5938:
5937:
5932:
5911:
5909:
5908:
5903:
5885:
5883:
5882:
5877:
5853:
5851:
5850:
5845:
5840:
5835:
5812:
5797:
5753:
5751:
5750:
5745:
5724:
5722:
5721:
5716:
5671:
5669:
5668:
5663:
5642:
5640:
5639:
5634:
5600:
5598:
5597:
5592:
5587:
5586:
5573:
5572:
5569:
5565:
5531:
5529:
5528:
5523:
5498:
5496:
5495:
5490:
5441:natural boundary
5415:Natural boundary
5343:
5341:
5340:
5335:
5333:
5329:
5322:
5314:
5306:
5298:
5293:
5285:
5277:
5269:
5264:
5256:
5198:
5196:
5195:
5190:
5188:
5187:
5166:
5161:
5160:
5159:
5134:
5131:
5126:
5077:
5075:
5074:
5069:
5067:
5066:
5049:
5047:
5046:
5041:
5039:
5038:
5025:
5023:
5022:
5017:
5015:
5014:
4985:
4983:
4982:
4977:
4972:
4955:
4954:
4942:
4941:
4920:
4919:
4897:
4895:
4894:
4889:
4887:
4886:
4866:
4864:
4863:
4858:
4856:
4855:
4838:
4836:
4835:
4830:
4828:
4827:
4790:
4788:
4787:
4782:
4768:
4763:
4762:
4750:
4749:
4740:
4720:
4719:
4692:
4691:
4673:> 0, and let
4668:
4666:
4665:
4660:
4658:
4657:
4641:We can define a
4637:
4635:
4634:
4629:
4610:the relation by
4573:
4571:
4570:
4565:
4557:
4552:
4551:
4539:
4538:
4529:
4497:
4495:
4494:
4489:
4487:
4486:
4430:is the value of
4353:
4351:
4350:
4345:
4334:
4333:
4321:
4320:
4308:
4307:
4295:
4294:
4254:
4252:
4251:
4246:
4235:
4230:
4229:
4214:
4206:
4186:
4185:
4173:
4172:
4123:
4121:
4120:
4115:
4113:
4112:
4103:
4102:
4084:
4083:
4073:
4068:
4002:
4000:
3999:
3994:
3968:
3966:
3965:
3960:
3943:
3931:
3929:
3928:
3923:
3911:
3909:
3908:
3903:
3891:
3889:
3888:
3883:
3865:
3863:
3862:
3857:
3845:
3843:
3842:
3837:
3811:
3809:
3808:
3803:
3783:
3774:
3758:
3756:
3755:
3750:
3738:
3736:
3735:
3730:
3718:
3716:
3715:
3710:
3698:
3696:
3695:
3690:
3682:
3674:
3662:
3660:
3659:
3654:
3636:
3634:
3633:
3628:
3616:
3614:
3613:
3608:
3606:
3598:
3584:
3582:
3581:
3576:
3574:
3570:
3568:
3542:
3534:
3530:
3522:
3514:
3510:
3508:
3507:
3503:
3502:
3494:
3471:
3469:
3461:
3453:
3449:
3448:
3443:
3439:
3438:
3430:
3415:
3410:
3395:
3387:
3379:
3375:
3374:
3353:
3352:
3334:
3333:
3314:
3309:
3288:
3284:
3283:
3262:
3261:
3251:
3246:
3199:
3197:
3196:
3191:
3186:
3185:
3176:
3175:
3174:
3165:
3153:
3145:
3140:
3122:
3120:
3119:
3118:
3087:
3077:geometric series
3074:
3068:
3066:
3065:
3060:
3055:
3051:
3050:
3032:
3031:
3007:
3003:
3002:
2981:
2980:
2979:
2970:
2958:
2950:
2945:
2930:
2929:
2905:
2901:
2900:
2873:
2872:
2871:
2858:
2851:
2850:
2831:
2826:
2805:
2794:
2786:
2777:
2776:
2749:
2748:
2747:
2734:
2727:
2726:
2707:
2702:
2687:
2685:
2674:
2666:
2656:
2655:
2627:
2619:
2610:
2609:
2594:
2593:
2566:
2565:
2564:
2551:
2543:
2538:
2523:
2522:
2503:
2498:
2483:
2481:
2470:
2462:
2458:
2456:
2455:
2454:
2445:
2444:
2425:
2418:
2417:
2408:
2407:
2389:
2388:
2361:
2360:
2359:
2346:
2338:
2333:
2317:
2314:
2306:
2297:
2296:
2277:
2272:
2257:
2255:
2244:
2236:
2232:
2230:
2229:
2228:
2219:
2218:
2199:
2192:
2191:
2182:
2181:
2150:
2147:
2139:
2130:
2129:
2110:
2105:
2090:
2088:
2077:
2069:
2065:
2063:
2062:
2061:
2046:
2045:
2026:
2019:
2018:
2000:
1999:
1984:
1983:
1958:
1955:
1947:
1938:
1937:
1918:
1913:
1898:
1896:
1882:
1874:
1870:
1868:
1867:
1866:
1838:
1831:
1830:
1808:
1806:
1805:
1793:
1792:
1773:
1768:
1753:
1751:
1737:
1729:
1725:
1723:
1722:
1721:
1693:
1686:
1685:
1664:
1663:
1644:
1639:
1623:
1621:
1620:
1608:
1606:
1592:
1584:
1580:
1578:
1577:
1576:
1548:
1528:
1526:
1525:
1513:
1511:
1497:
1489:
1485:
1483:
1475:
1465:
1464:
1448:
1439:
1438:
1414:
1412:
1411:
1406:
1379:
1377:
1376:
1371:
1356:
1354:
1353:
1348:
1336:
1334:
1333:
1328:
1316:
1314:
1313:
1308:
1296:
1294:
1293:
1288:
1264:
1262:
1261:
1256:
1248:
1234:
1210:
1208:
1207:
1202:
1187:
1185:
1184:
1179:
1164:
1162:
1161:
1156:
1144:
1142:
1141:
1136:
1118:
1116:
1115:
1110:
1098:
1096:
1095:
1090:
1078:
1076:
1075:
1070:
1058:
1056:
1055:
1050:
1048:
1047:
1029:
1027:
1026:
1021:
1016:
1015:
994:
993:
983:
978:
939:
937:
936:
931:
913:
911:
910:
905:
900:
867:
865:
864:
859:
832:
830:
829:
824:
813:
799:
775:
773:
772:
767:
756:
742:
721:
719:
718:
713:
695:
693:
692:
687:
682:
681:
660:
659:
640:
635:
596:
594:
593:
588:
566:
564:
563:
558:
502:Riemann surfaces
460:identity theorem
428:
426:
425:
420:
418:
417:
405:
404:
382:
380:
379:
374:
345:
344:
323:
322:
293:is contained in
260:is the function
236:
234:
233:
228:
161:
159:
157:
156:
151:
149:
132:
130:
128:
127:
122:
120:
72:sheaf cohomology
32:complex analysis
21:
8890:
8889:
8885:
8884:
8883:
8881:
8880:
8879:
8875:Generalizations
8855:
8854:
8836:
8835:
8811:
8808:
8795:
8786:
8774:
8771:
8770:
8757:
8753:
8726:Physical Review
8719:
8718:
8714:
8709:
8687:
8677:
8644:
8634:
8615:
8605:
8564:
8563:
8558:
8527:
8517:
8498:
8457:
8456:
8450:
8448:Pólya's theorem
8401:
8385:
8362:
8361:
8332:
8327:
8317:
8276:
8275:
8269:
8263:
8157:
8156:
8146:
8140:
8098:
8097:
8063:
8058:
8057:
8002:
7997:
7996:
7956:
7951:
7950:
7897:
7882:
7877:
7859:
7825:
7820:
7803:
7788:
7783:
7765:
7723:
7699:
7685:
7684:
7646:
7645:
7611:
7606:
7605:
7576:
7571:
7566:
7565:
7559:complex numbers
7537:
7532:
7531:
7510:
7482:
7472:
7471:
7450:
7449:
7409:
7404:
7376:
7372:
7349:
7344:
7343:
7315:
7314:
7289:
7288:
7247:
7242:
7241:
7220:
7215:
7214:
7180:
7175:
7174:
7173:, the function
7149:
7148:
7113:
7112:
7074:
7069:
7068:
7043:
7042:
6984:
6979:
6962:
6947:
6942:
6889:
6884:
6883:
6846:
6841:
6840:
6815:
6814:
6790:
6773:
6760:
6734:
6729:
6728:
6693:
6692:
6654:
6649:
6648:
6627:
6602:
6597:
6596:
6595:Clearly, since
6548:
6543:
6501:
6496:
6495:
6485:lacunary series
6459:
6458:
6455:
6422:
6421:
6396:
6395:
6374:
6300:
6295:
6294:
6260:
6259:
6231:
6230:
6198:
6197:
6169:
6168:
6143:
6142:
6074:
6070:
6050:
6028:
6027:
6023:
6010:
6005:
6004:
5978:
5943:
5942:
5914:
5913:
5888:
5887:
5859:
5858:
5813:
5763:
5762:
5727:
5726:
5686:
5685:
5678:natural numbers
5645:
5644:
5610:
5609:
5575:
5537:
5536:
5505:
5504:
5466:
5465:
5462:
5417:
5233:
5229:
5218:
5217:
5179:
5145:
5135:
5092:
5091:
5088:
5056:
5055:
5052:Riemann surface
5028:
5027:
5004:
5003:
4946:
4933:
4911:
4906:
4905:
4876:
4875:
4845:
4844:
4811:
4810:
4799:
4754:
4741:
4683:
4678:
4677:
4647:
4646:
4620:
4619:
4598:, and we write
4543:
4530:
4520:
4519:
4504:
4476:
4475:
4469:
4462:
4458:
4454:
4440:
4425:
4417:
4408:, ...) and the
4407:
4403:
4399:
4387:
4376:
4325:
4312:
4299:
4286:
4272:
4271:
4221:
4177:
4164:
4159:
4158:
4149:
4142:
4104:
4094:
4075:
4034:
4033:
4017:
3973:
3972:
3934:
3933:
3914:
3913:
3894:
3893:
3868:
3867:
3848:
3847:
3816:
3815:
3761:
3760:
3741:
3740:
3721:
3720:
3701:
3700:
3665:
3664:
3639:
3638:
3637:. If we choose
3619:
3618:
3589:
3588:
3572:
3571:
3546:
3532:
3531:
3512:
3511:
3486:
3482:
3475:
3451:
3450:
3422:
3418:
3417:
3377:
3376:
3366:
3335:
3325:
3286:
3285:
3275:
3253:
3225:
3204:
3203:
3177:
3155:
3148:
3104:
3091:
3081:
3080:
3072:
3053:
3052:
3033:
3023:
3005:
3004:
2994:
2960:
2953:
2921:
2903:
2902:
2886:
2853:
2842:
2803:
2802:
2762:
2729:
2718:
2678:
2664:
2663:
2629:
2595:
2579:
2546:
2514:
2474:
2460:
2459:
2446:
2433:
2426:
2409:
2396:
2374:
2341:
2318:
2288:
2248:
2234:
2233:
2220:
2207:
2200:
2183:
2170:
2151:
2121:
2081:
2067:
2066:
2047:
2034:
2027:
2007:
1991:
1972:
1959:
1929:
1886:
1872:
1871:
1852:
1839:
1822:
1809:
1794:
1784:
1741:
1727:
1726:
1707:
1694:
1677:
1655:
1624:
1609:
1596:
1582:
1581:
1562:
1549:
1529:
1514:
1501:
1487:
1486:
1476:
1450:
1449:
1440:
1430:
1421:
1420:
1382:
1381:
1359:
1358:
1339:
1338:
1319:
1318:
1299:
1298:
1267:
1266:
1213:
1212:
1190:
1189:
1170:
1169:
1147:
1146:
1121:
1120:
1101:
1100:
1081:
1080:
1061:
1060:
1039:
1034:
1033:
1007:
985:
944:
943:
916:
915:
873:
872:
835:
834:
778:
777:
724:
723:
704:
703:
673:
651:
601:
600:
573:
572:
549:
548:
529:
511:, solutions of
494:universal cover
472:
449:
442:
409:
396:
391:
390:
336:
314:
309:
308:
288:
281:
179:
178:
140:
139:
138:
111:
110:
109:
80:
52:infinite series
28:
23:
22:
15:
12:
11:
5:
8888:
8886:
8878:
8877:
8872:
8867:
8857:
8856:
8853:
8852:
8833:
8827:
8807:
8806:External links
8804:
8803:
8802:
8793:
8784:
8769:
8768:
8751:
8711:
8710:
8708:
8705:
8704:
8703:
8698:
8693:
8686:
8683:
8675:
8665:
8664:
8651:
8647:
8641:
8637:
8633:
8630:
8627:
8622:
8618:
8612:
8608:
8602:
8597:
8594:
8591:
8587:
8583:
8580:
8577:
8574:
8571:
8554:
8548:
8547:
8534:
8530:
8524:
8520:
8516:
8513:
8510:
8505:
8501:
8495:
8490:
8487:
8484:
8480:
8476:
8473:
8470:
8467:
8464:
8449:
8446:
8430:
8429:
8418:
8415:
8408:
8404:
8398:
8395:
8392:
8388:
8380:
8377:
8374:
8370:
8369:lim inf
8355:
8354:
8339:
8335:
8330:
8324:
8320:
8314:
8309:
8306:
8303:
8299:
8295:
8292:
8289:
8286:
8283:
8265:Main article:
8262:
8259:
8171:
8167:
8164:
8142:Main article:
8139:
8136:
8123:
8120:
8117:
8112:
8108:
8105:
8085:
8082:
8079:
8074:
8068:
8045:
8042:
8039:
8035:
8031:
8027:
8023:
8020:
8017:
8014:
8009:
8005:
7984:
7981:
7978:
7975:
7972:
7967:
7961:
7943:
7942:
7931:
7928:
7925:
7922:
7919:
7916:
7913:
7908:
7902:
7896:
7889:
7885:
7880:
7874:
7871:
7866:
7862:
7856:
7853:
7850:
7846:
7842:
7839:
7832:
7828:
7823:
7819:
7814:
7808:
7802:
7795:
7791:
7786:
7780:
7777:
7772:
7768:
7762:
7759:
7756:
7752:
7748:
7745:
7742:
7739:
7734:
7728:
7721:
7716:
7713:
7710:
7704:
7698:
7695:
7692:
7669:
7666:
7662:
7658:
7654:
7633:
7630:
7627:
7622:
7616:
7593:
7590:
7583:
7579:
7574:
7544:
7540:
7517:
7513:
7509:
7505:
7499:
7496:
7493:
7487:
7480:
7458:
7446:
7445:
7434:
7430:
7426:
7423:
7416:
7412:
7407:
7403:
7398:
7393:
7390:
7386:
7382:
7379:
7375:
7371:
7366:
7363:
7360:
7354:
7328:
7325:
7322:
7302:
7299:
7296:
7269:
7266:
7263:
7258:
7252:
7227:
7223:
7202:
7199:
7196:
7191:
7185:
7162:
7159:
7156:
7136:
7133:
7129:
7125:
7121:
7096:
7093:
7090:
7085:
7079:
7056:
7053:
7050:
7035:
7034:
7023:
7020:
7016:
7012:
7008:
7004:
7001:
6998:
6991:
6987:
6982:
6978:
6973:
6967:
6961:
6954:
6950:
6945:
6939:
6936:
6933:
6928:
6925:
6922:
6918:
6914:
6911:
6908:
6905:
6900:
6894:
6868:
6865:
6862:
6857:
6851:
6828:
6825:
6822:
6802:
6797:
6793:
6789:
6784:
6778:
6772:
6767:
6763:
6759:
6756:
6753:
6750:
6745:
6739:
6716:
6713:
6709:
6705:
6701:
6676:
6673:
6670:
6665:
6659:
6634:
6630:
6626:
6623:
6620:
6615:
6612:
6609:
6605:
6593:
6592:
6581:
6578:
6574:
6570:
6566:
6562:
6555:
6551:
6546:
6540:
6537:
6534:
6530:
6526:
6523:
6520:
6517:
6512:
6506:
6472:
6469:
6466:
6454:
6451:
6438:
6435:
6432:
6429:
6409:
6406:
6403:
6381:
6377:
6373:
6370:
6367:
6364:
6361:
6358:
6355:
6352:
6349:
6346:
6343:
6340:
6337:
6334:
6331:
6316:
6312:
6307:
6303:
6282:
6279:
6276:
6273:
6270:
6267:
6247:
6244:
6241:
6238:
6214:
6211:
6208:
6205:
6185:
6182:
6179:
6176:
6156:
6153:
6150:
6139:
6138:
6126:
6122:
6119:
6114:
6111:
6106:
6101:
6098:
6093:
6088:
6085:
6080:
6077:
6073:
6069:
6065:
6059:
6054:
6049:
6046:
6043:
6038:
6035:
6031:
6026:
6022:
6017:
6013:
5987:
5982:
5977:
5974:
5971:
5968:
5962:
5959:
5953:
5950:
5930:
5927:
5924:
5921:
5901:
5898:
5895:
5875:
5872:
5869:
5866:
5855:
5854:
5843:
5838:
5834:
5831:
5828:
5825:
5822:
5819:
5816:
5810:
5807:
5804:
5801:
5796:
5793:
5790:
5786:
5782:
5779:
5776:
5773:
5770:
5743:
5740:
5737:
5734:
5714:
5711:
5708:
5705:
5702:
5699:
5696:
5693:
5661:
5658:
5655:
5652:
5632:
5629:
5626:
5623:
5620:
5617:
5602:
5601:
5590:
5585:
5582:
5578:
5564:
5560:
5556:
5553:
5550:
5547:
5544:
5521:
5518:
5515:
5512:
5488:
5485:
5482:
5479:
5476:
5473:
5461:
5458:
5416:
5413:
5345:
5344:
5332:
5328:
5325:
5320:
5317:
5312:
5309:
5304:
5301:
5296:
5291:
5288:
5283:
5280:
5275:
5272:
5267:
5262:
5259:
5254:
5251:
5248:
5245:
5242:
5239:
5236:
5232:
5228:
5225:
5200:
5199:
5186:
5182:
5178:
5175:
5172:
5169:
5164:
5158:
5155:
5152:
5148:
5144:
5141:
5138:
5130:
5125:
5122:
5119:
5115:
5111:
5108:
5105:
5102:
5099:
5087:
5084:
5065:
5037:
5013:
4975:
4971:
4967:
4964:
4961:
4958:
4953:
4949:
4945:
4940:
4936:
4932:
4929:
4926:
4923:
4918:
4914:
4885:
4854:
4826:
4821:
4818:
4797:
4792:
4791:
4780:
4777:
4774:
4771:
4767:
4761:
4757:
4753:
4748:
4744:
4739:
4735:
4732:
4729:
4726:
4723:
4718:
4713:
4710:
4707:
4704:
4701:
4698:
4695:
4690:
4686:
4656:
4627:
4563:
4560:
4556:
4550:
4546:
4542:
4537:
4533:
4528:
4503:
4500:
4485:
4467:
4460:
4456:
4452:
4438:
4423:
4415:
4405:
4401:
4397:
4385:
4374:
4355:
4354:
4343:
4340:
4337:
4332:
4328:
4324:
4319:
4315:
4311:
4306:
4302:
4298:
4293:
4289:
4285:
4282:
4279:
4257:
4256:
4244:
4241:
4238:
4234:
4228:
4224:
4220:
4217:
4213:
4209:
4205:
4201:
4198:
4195:
4192:
4189:
4184:
4180:
4176:
4171:
4167:
4147:
4138:
4125:
4124:
4111:
4107:
4101:
4097:
4093:
4090:
4087:
4082:
4078:
4072:
4067:
4064:
4061:
4057:
4053:
4050:
4047:
4044:
4041:
4016:
4013:
4009:antiderivative
3992:
3989:
3986:
3983:
3980:
3958:
3955:
3952:
3949:
3946:
3942:
3921:
3901:
3881:
3878:
3875:
3855:
3835:
3832:
3829:
3826:
3823:
3801:
3798:
3795:
3792:
3789:
3786:
3780:
3777:
3771:
3768:
3748:
3728:
3708:
3688:
3685:
3681:
3677:
3673:
3652:
3649:
3646:
3626:
3605:
3601:
3597:
3567:
3564:
3561:
3558:
3555:
3552:
3549:
3545:
3540:
3537:
3535:
3533:
3528:
3525:
3520:
3517:
3515:
3513:
3506:
3500:
3497:
3492:
3489:
3485:
3481:
3478:
3474:
3467:
3464:
3459:
3456:
3454:
3452:
3447:
3442:
3436:
3433:
3428:
3425:
3421:
3414:
3409:
3406:
3403:
3399:
3393:
3390:
3385:
3382:
3380:
3378:
3373:
3369:
3365:
3362:
3359:
3356:
3351:
3348:
3345:
3342:
3338:
3332:
3328:
3324:
3321:
3318:
3313:
3308:
3305:
3302:
3298:
3294:
3291:
3289:
3287:
3282:
3278:
3274:
3271:
3268:
3265:
3260:
3256:
3250:
3245:
3242:
3239:
3235:
3231:
3228:
3226:
3224:
3221:
3218:
3215:
3212:
3211:
3189:
3184:
3180:
3173:
3168:
3164:
3161:
3158:
3152:
3144:
3139:
3136:
3133:
3129:
3125:
3117:
3114:
3111:
3107:
3103:
3100:
3097:
3094:
3090:
3058:
3049:
3046:
3043:
3040:
3036:
3030:
3026:
3022:
3019:
3016:
3013:
3010:
3008:
3006:
3001:
2997:
2993:
2990:
2987:
2984:
2978:
2973:
2969:
2966:
2963:
2957:
2949:
2944:
2941:
2938:
2934:
2928:
2924:
2920:
2917:
2914:
2911:
2908:
2906:
2904:
2899:
2896:
2893:
2889:
2885:
2882:
2879:
2876:
2870:
2865:
2862:
2857:
2849:
2845:
2841:
2838:
2835:
2830:
2825:
2822:
2819:
2815:
2811:
2808:
2806:
2804:
2801:
2798:
2793:
2790:
2785:
2781:
2775:
2772:
2769:
2765:
2761:
2758:
2755:
2752:
2746:
2741:
2738:
2733:
2725:
2721:
2717:
2714:
2711:
2706:
2701:
2698:
2695:
2691:
2684:
2681:
2677:
2672:
2669:
2667:
2665:
2662:
2659:
2654:
2651:
2648:
2645:
2642:
2639:
2636:
2632:
2626:
2623:
2618:
2614:
2608:
2605:
2602:
2598:
2592:
2589:
2586:
2582:
2578:
2575:
2572:
2569:
2563:
2558:
2555:
2550:
2542:
2537:
2534:
2531:
2527:
2521:
2517:
2513:
2510:
2507:
2502:
2497:
2494:
2491:
2487:
2480:
2477:
2473:
2468:
2465:
2463:
2461:
2453:
2449:
2443:
2440:
2436:
2432:
2429:
2424:
2421:
2416:
2412:
2406:
2403:
2399:
2395:
2392:
2387:
2384:
2381:
2377:
2373:
2370:
2367:
2364:
2358:
2353:
2350:
2345:
2337:
2332:
2329:
2326:
2322:
2313:
2310:
2305:
2301:
2295:
2291:
2287:
2284:
2281:
2276:
2271:
2268:
2265:
2261:
2254:
2251:
2247:
2242:
2239:
2237:
2235:
2227:
2223:
2217:
2214:
2210:
2206:
2203:
2198:
2195:
2190:
2186:
2180:
2177:
2173:
2169:
2166:
2163:
2160:
2157:
2154:
2146:
2143:
2138:
2134:
2128:
2124:
2120:
2117:
2114:
2109:
2104:
2101:
2098:
2094:
2087:
2084:
2080:
2075:
2072:
2070:
2068:
2060:
2057:
2054:
2050:
2044:
2041:
2037:
2033:
2030:
2025:
2022:
2017:
2014:
2010:
2006:
2003:
1998:
1994:
1990:
1987:
1982:
1979:
1975:
1971:
1968:
1965:
1962:
1954:
1951:
1946:
1942:
1936:
1932:
1928:
1925:
1922:
1917:
1912:
1909:
1906:
1902:
1895:
1892:
1889:
1885:
1880:
1877:
1875:
1873:
1865:
1862:
1859:
1855:
1851:
1848:
1845:
1842:
1837:
1834:
1829:
1825:
1821:
1818:
1815:
1812:
1804:
1801:
1797:
1791:
1787:
1783:
1780:
1777:
1772:
1767:
1764:
1761:
1757:
1750:
1747:
1744:
1740:
1735:
1732:
1730:
1728:
1720:
1717:
1714:
1710:
1706:
1703:
1700:
1697:
1692:
1689:
1684:
1680:
1676:
1673:
1670:
1667:
1662:
1658:
1654:
1651:
1648:
1643:
1638:
1635:
1632:
1628:
1619:
1616:
1612:
1605:
1602:
1599:
1595:
1590:
1587:
1585:
1583:
1575:
1572:
1569:
1565:
1561:
1558:
1555:
1552:
1547:
1544:
1541:
1538:
1535:
1532:
1524:
1521:
1517:
1510:
1507:
1504:
1500:
1495:
1492:
1490:
1488:
1482:
1479:
1474:
1471:
1468:
1463:
1460:
1457:
1453:
1446:
1443:
1441:
1437:
1433:
1429:
1428:
1404:
1401:
1398:
1395:
1392:
1389:
1369:
1366:
1346:
1326:
1306:
1286:
1283:
1280:
1277:
1274:
1254:
1251:
1247:
1243:
1240:
1237:
1233:
1229:
1226:
1223:
1220:
1200:
1197:
1177:
1154:
1134:
1131:
1128:
1119:to the region
1108:
1088:
1068:
1046:
1042:
1019:
1014:
1010:
1006:
1003:
1000:
997:
992:
988:
982:
977:
974:
971:
967:
963:
960:
957:
954:
951:
929:
926:
923:
903:
899:
895:
892:
889:
886:
883:
880:
857:
854:
851:
848:
845:
842:
822:
819:
816:
812:
808:
805:
802:
798:
794:
791:
788:
785:
765:
762:
759:
755:
751:
748:
745:
741:
737:
734:
731:
711:
685:
680:
676:
672:
669:
666:
663:
658:
654:
650:
647:
644:
639:
634:
631:
628:
624:
620:
617:
614:
611:
608:
586:
583:
580:
556:
528:
527:Worked example
525:
487:gamma function
471:
468:
447:
440:
430:
429:
416:
412:
408:
403:
399:
384:
383:
372:
369:
366:
363:
360:
357:
354:
351:
348:
343:
339:
335:
332:
329:
326:
321:
317:
286:
279:
238:
237:
226:
223:
220:
217:
214:
210:
207:
204:
201:
198:
195:
192:
189:
186:
148:
119:
79:
76:
66:. The case of
34:, a branch of
26:
24:
14:
13:
10:
9:
6:
4:
3:
2:
8887:
8876:
8873:
8871:
8868:
8866:
8863:
8862:
8860:
8848:
8847:
8842:
8839:
8834:
8831:
8828:
8824:
8820:
8819:
8814:
8810:
8809:
8805:
8799:
8794:
8790:
8785:
8781:
8777:
8773:
8772:
8765:
8761:
8755:
8752:
8747:
8743:
8739:
8735:
8731:
8727:
8723:
8716:
8713:
8706:
8702:
8699:
8697:
8694:
8692:
8689:
8688:
8684:
8682:
8679:
8674:
8670:
8649:
8639:
8635:
8631:
8628:
8620:
8616:
8610:
8606:
8595:
8592:
8589:
8585:
8581:
8575:
8569:
8562:
8561:
8560:
8557:
8553:
8532:
8522:
8518:
8514:
8511:
8503:
8499:
8488:
8485:
8482:
8478:
8474:
8468:
8462:
8455:
8454:
8453:
8445:
8443:
8439:
8435:
8416:
8413:
8406:
8402:
8396:
8393:
8390:
8386:
8372:
8360:
8359:
8358:
8337:
8333:
8328:
8322:
8318:
8307:
8304:
8301:
8297:
8293:
8287:
8281:
8274:
8273:
8272:
8268:
8258:
8256:
8252:
8248:
8244:
8240:
8236:
8231:
8229:
8225:
8221:
8217:
8213:
8209:
8205:
8201:
8198:
8194:
8190:
8186:
8165:
8162:
8153:
8151:
8145:
8137:
8135:
8121:
8118:
8115:
8106:
8103:
8080:
8072:
8040:
8037:
8029:
8021:
8018:
8012:
8007:
8003:
7979:
7973:
7965:
7948:
7929:
7923:
7920:
7914:
7906:
7894:
7887:
7883:
7878:
7872:
7869:
7864:
7860:
7854:
7851:
7848:
7844:
7840:
7830:
7826:
7821:
7812:
7800:
7793:
7789:
7784:
7778:
7775:
7770:
7766:
7760:
7757:
7754:
7750:
7746:
7740:
7732:
7719:
7714:
7711:
7708:
7696:
7693:
7683:
7682:
7681:
7680:to show that
7667:
7664:
7656:
7628:
7620:
7591:
7588:
7581:
7577:
7572:
7563:
7560:
7542:
7538:
7515:
7511:
7507:
7497:
7494:
7491:
7432:
7428:
7424:
7421:
7414:
7410:
7405:
7401:
7388:
7380:
7377:
7373:
7369:
7364:
7361:
7358:
7342:
7341:
7340:
7326:
7323:
7320:
7300:
7297:
7294:
7285:
7283:
7264:
7256:
7225:
7221:
7197:
7189:
7160:
7157:
7154:
7134:
7131:
7123:
7110:
7091:
7083:
7054:
7051:
7048:
7040:
7021:
7018:
7010:
6999:
6989:
6985:
6980:
6971:
6959:
6952:
6948:
6943:
6937:
6934:
6931:
6926:
6923:
6920:
6916:
6912:
6906:
6898:
6882:
6881:
6880:
6863:
6855:
6826:
6823:
6820:
6795:
6791:
6782:
6770:
6765:
6761:
6757:
6751:
6743:
6714:
6711:
6703:
6690:
6671:
6663:
6632:
6628:
6624:
6621:
6618:
6613:
6610:
6607:
6603:
6579:
6576:
6568:
6560:
6553:
6549:
6544:
6538:
6535:
6532:
6528:
6524:
6518:
6510:
6494:
6493:
6492:
6490:
6486:
6470:
6467:
6464:
6457:For integers
6452:
6450:
6433:
6427:
6407:
6404:
6401:
6379:
6375:
6371:
6368:
6362:
6356:
6353:
6350:
6347:
6341:
6335:
6310:
6305:
6301:
6277:
6268:
6265:
6242:
6236:
6228:
6209:
6203:
6180:
6174:
6148:
6124:
6120:
6117:
6112:
6109:
6104:
6099:
6096:
6091:
6086:
6083:
6078:
6075:
6071:
6067:
6063:
6057:
6047:
6044:
6041:
6036:
6033:
6029:
6024:
6020:
6015:
6011:
6003:
6002:
6001:
5985:
5975:
5972:
5966:
5960:
5957:
5951:
5948:
5925:
5919:
5899:
5896:
5893:
5870:
5864:
5841:
5836:
5829:
5826:
5820:
5817:
5814:
5805:
5799:
5794:
5791:
5788:
5784:
5780:
5774:
5768:
5761:
5760:
5759:
5757:
5738:
5732:
5712:
5709:
5703:
5694:
5691:
5683:
5679:
5675:
5674:prime numbers
5656:
5650:
5630:
5627:
5621:
5607:
5588:
5583:
5580:
5576:
5562:
5558:
5554:
5548:
5542:
5535:
5534:
5533:
5516:
5510:
5502:
5486:
5483:
5477:
5459:
5457:
5455:
5454:
5449:
5444:
5442:
5438:
5434:
5430:
5426:
5422:
5414:
5412:
5410:
5406:
5405:
5399:
5397:
5393:
5389:
5385:
5381:
5377:
5373:
5369:
5365:
5362:of the sheaf
5361:
5355:
5353:
5350:
5330:
5326:
5323:
5318:
5315:
5310:
5307:
5302:
5299:
5294:
5289:
5286:
5281:
5278:
5273:
5270:
5265:
5260:
5257:
5252:
5249:
5246:
5243:
5240:
5237:
5234:
5230:
5226:
5223:
5216:
5215:
5214:
5213:
5209:
5205:
5184:
5176:
5173:
5170:
5162:
5156:
5153:
5150:
5142:
5139:
5123:
5120:
5117:
5113:
5109:
5103:
5097:
5090:
5089:
5085:
5083:
5081:
5053:
5001:
4997:
4993:
4989:
4973:
4959:
4951:
4947:
4943:
4938:
4934:
4930:
4924:
4916:
4912:
4903:
4902:
4873:
4868:
4842:
4819:
4816:
4808:
4804:
4800:
4778:
4772:
4769:
4759:
4755:
4751:
4746:
4742:
4733:
4730:
4727:
4724:
4721:
4711:
4708:
4702:
4696:
4688:
4684:
4676:
4675:
4674:
4672:
4644:
4639:
4625:
4617:
4613:
4609:
4605:
4601:
4597:
4593:
4589:
4585:
4581:
4577:
4561:
4558:
4548:
4544:
4540:
4535:
4531:
4517:
4513:
4509:
4501:
4499:
4473:
4466:
4451:
4447:
4442:
4437:
4433:
4429:
4426:. The top of
4421:
4414:
4411:
4395:
4391:
4384:
4380:
4373:
4370:
4366:
4362:
4361:
4338:
4335:
4330:
4326:
4322:
4317:
4313:
4309:
4304:
4300:
4296:
4291:
4287:
4280:
4277:
4270:
4269:
4268:
4266:
4262:
4239:
4236:
4226:
4222:
4218:
4215:
4207:
4199:
4196:
4190:
4182:
4178:
4169:
4165:
4157:
4156:
4155:
4153:
4146:
4141:
4137:
4134:
4130:
4109:
4099:
4095:
4091:
4088:
4080:
4076:
4065:
4062:
4059:
4055:
4051:
4045:
4039:
4032:
4031:
4030:
4028:
4024:
4023:
4014:
4012:
4010:
4006:
3987:
3984:
3978:
3969:
3956:
3950:
3919:
3899:
3879:
3876:
3873:
3853:
3833:
3830:
3827:
3824:
3821:
3812:
3799:
3793:
3790:
3787:
3778:
3775:
3769:
3766:
3746:
3726:
3706:
3686:
3683:
3675:
3650:
3647:
3644:
3624:
3599:
3585:
3565:
3562:
3556:
3553:
3550:
3543:
3538:
3536:
3526:
3523:
3518:
3516:
3504:
3498:
3495:
3490:
3487:
3483:
3479:
3476:
3472:
3465:
3462:
3457:
3455:
3445:
3440:
3434:
3431:
3426:
3423:
3419:
3407:
3404:
3401:
3397:
3391:
3388:
3383:
3381:
3371:
3363:
3360:
3357:
3349:
3346:
3343:
3340:
3336:
3330:
3322:
3319:
3306:
3303:
3300:
3296:
3292:
3290:
3280:
3272:
3269:
3266:
3258:
3254:
3243:
3240:
3237:
3233:
3229:
3227:
3219:
3213:
3200:
3187:
3182:
3178:
3166:
3162:
3159:
3156:
3137:
3134:
3131:
3127:
3123:
3115:
3112:
3109:
3101:
3098:
3095:
3088:
3078:
3069:
3056:
3047:
3044:
3041:
3038:
3034:
3028:
3020:
3017:
3011:
3009:
2999:
2991:
2988:
2985:
2971:
2967:
2964:
2961:
2942:
2939:
2936:
2932:
2926:
2918:
2915:
2909:
2907:
2897:
2894:
2891:
2883:
2880:
2877:
2863:
2860:
2847:
2839:
2836:
2823:
2820:
2817:
2813:
2809:
2807:
2799:
2796:
2791:
2788:
2783:
2779:
2773:
2770:
2767:
2759:
2756:
2753:
2739:
2736:
2723:
2715:
2712:
2699:
2696:
2693:
2689:
2682:
2679:
2675:
2670:
2668:
2660:
2657:
2652:
2646:
2643:
2640:
2634:
2630:
2624:
2621:
2616:
2612:
2606:
2603:
2600:
2596:
2590:
2587:
2584:
2576:
2573:
2570:
2556:
2553:
2540:
2535:
2532:
2529:
2525:
2519:
2511:
2508:
2495:
2492:
2489:
2485:
2478:
2475:
2471:
2466:
2464:
2451:
2441:
2438:
2434:
2430:
2422:
2419:
2414:
2404:
2401:
2397:
2393:
2385:
2382:
2379:
2371:
2368:
2365:
2351:
2348:
2335:
2330:
2327:
2324:
2320:
2311:
2308:
2303:
2299:
2293:
2285:
2282:
2269:
2266:
2263:
2259:
2252:
2249:
2245:
2240:
2238:
2225:
2215:
2212:
2208:
2204:
2196:
2193:
2188:
2178:
2175:
2171:
2167:
2164:
2161:
2158:
2155:
2144:
2141:
2136:
2132:
2126:
2118:
2115:
2102:
2099:
2096:
2092:
2085:
2082:
2078:
2073:
2071:
2058:
2055:
2052:
2042:
2039:
2035:
2031:
2023:
2020:
2015:
2012:
2008:
2004:
2001:
1996:
1988:
1985:
1980:
1977:
1973:
1969:
1966:
1963:
1952:
1949:
1944:
1940:
1934:
1926:
1923:
1910:
1907:
1904:
1900:
1893:
1890:
1887:
1883:
1878:
1876:
1863:
1860:
1857:
1849:
1846:
1843:
1835:
1832:
1827:
1819:
1816:
1813:
1802:
1795:
1789:
1781:
1778:
1765:
1762:
1759:
1755:
1748:
1745:
1742:
1738:
1733:
1731:
1718:
1715:
1712:
1704:
1701:
1698:
1690:
1687:
1682:
1674:
1671:
1668:
1660:
1652:
1649:
1636:
1633:
1630:
1626:
1617:
1610:
1603:
1600:
1597:
1593:
1588:
1586:
1573:
1570:
1567:
1559:
1556:
1553:
1545:
1542:
1536:
1530:
1522:
1515:
1508:
1505:
1502:
1498:
1493:
1491:
1480:
1477:
1469:
1458:
1451:
1444:
1442:
1435:
1431:
1418:
1402:
1399:
1396:
1390:
1387:
1367:
1344:
1324:
1304:
1284:
1281:
1278:
1275:
1272:
1252:
1249:
1241:
1238:
1235:
1227:
1224:
1221:
1218:
1198:
1175:
1166:
1152:
1132:
1129:
1126:
1106:
1086:
1066:
1044:
1040:
1030:
1017:
1012:
1004:
1001:
998:
990:
986:
975:
972:
969:
965:
961:
955:
949:
941:
927:
924:
921:
901:
897:
893:
890:
884:
878:
869:
855:
849:
846:
843:
840:
817:
814:
806:
803:
800:
789:
786:
760:
757:
749:
746:
743:
732:
729:
709:
701:
696:
683:
678:
670:
667:
664:
656:
648:
645:
632:
629:
626:
622:
618:
612:
606:
598:
584:
581:
578:
570:
554:
542:
538:
533:
526:
524:
522:
518:
514:
510:
505:
503:
499:
495:
490:
488:
484:
480:
475:
469:
467:
465:
461:
457:
453:
446:
443: −
439:
435:
414:
410:
406:
401:
397:
389:
388:
387:
370:
364:
358:
355:
349:
341:
337:
333:
327:
319:
315:
307:
306:
305:
304:
300:
296:
292:
285:
278:
274:
270:
265:
263:
259:
255:
251:
247:
243:
224:
221:
218:
215:
205:
199:
196:
190:
184:
177:
176:
175:
173:
169:
165:
136:
108:
107:complex plane
104:
101:
97:
93:
84:
77:
75:
73:
69:
65:
64:singularities
59:
57:
53:
49:
45:
41:
37:
33:
19:
8844:
8832:at MathPages
8816:
8797:
8788:
8779:
8776:Lars Ahlfors
8759:
8754:
8729:
8725:
8715:
8680:
8672:
8668:
8666:
8555:
8551:
8549:
8451:
8442:George Pólya
8431:
8356:
8270:
8254:
8250:
8246:
8242:
8238:
8234:
8232:
8227:
8223:
8219:
8215:
8211:
8207:
8206:, such that
8203:
8192:
8188:
8184:
8154:
8149:
8147:
7946:
7944:
7561:
7447:
7286:
7281:
7108:
7038:
7036:
6688:
6594:
6488:
6456:
6226:
6140:
5856:
5681:
5603:
5463:
5451:
5447:
5445:
5440:
5436:
5435:, otherwise
5432:
5428:
5424:
5420:
5418:
5402:
5400:
5395:
5391:
5383:
5379:
5375:
5371:
5367:
5363:
5359:
5356:
5351:
5346:
5207:
5201:
5079:
4991:
4987:
4899:
4869:
4806:
4802:
4795:
4793:
4670:
4640:
4612:transitivity
4603:
4599:
4595:
4591:
4587:
4583:
4579:
4575:
4511:
4507:
4505:
4471:
4464:
4449:
4445:
4443:
4435:
4431:
4427:
4419:
4412:
4409:
4393:
4389:
4382:
4378:
4371:
4368:
4364:
4358:
4356:
4264:
4260:
4258:
4151:
4144:
4139:
4135:
4129:power series
4126:
4027:sheaf theory
4020:
4018:
3970:
3813:
3586:
3201:
3070:
1167:
1031:
942:
870:
697:
599:
571:centered at
569:power series
546:
540:
536:
506:
491:
476:
473:
470:Applications
455:
451:
444:
437:
433:
431:
385:
302:
298:
297:and for all
294:
290:
283:
276:
268:
266:
261:
257:
253:
245:
241:
239:
171:
167:
163:
134:
102:
91:
89:
60:
39:
29:
8202:containing
7280:to complex
6691:satisfying
5570: prime
4809:> 0 and
4805:), for all
4444:Any vector
250:restriction
162:containing
100:open subset
46:of a given
36:mathematics
8859:Categories
8707:References
7111:such that
5684:such that
1357:; and let
432:on all of
289:such that
174:such that
8846:MathWorld
8823:EMS Press
8762:page for
8760:MathWorld
8632:−
8617:α
8607:ε
8601:∞
8586:∑
8515:−
8500:α
8494:∞
8479:∑
8379:∞
8376:→
8313:∞
8298:∑
8166:⊂
8107:∈
7983:∞
7927:∞
7870:−
7845:∑
7776:−
7751:∑
7697:∈
7691:∀
7557:distinct
7392:∂
7389:∪
7381:∈
7324:≥
7158:≥
7003:∀
6935:−
6917:∑
6879:given by
6824:≥
6727:given by
6625:⋅
6536:≥
6529:∑
6487:of order
6468:≥
6394:for some
6372:∈
6366:∀
6348:−
6342:∈
6330:ℜ
6323:such that
6311:⊆
6272:ℜ
6269:≥
6155:∞
6152:↦
6121:…
6048:∈
6034:−
5976:∈
5970:∀
5865:ζ
5821:ζ
5818:
5800:μ
5792:≥
5785:∑
5698:ℜ
5651:ζ
5616:ℜ
5581:−
5559:∑
5472:ℜ
5327:…
5311:−
5282:−
5253:−
5174:−
5140:−
5129:∞
5114:∑
4966:→
4913:ϕ
4839:define a
4820:∈
4794:The sets
4752:−
4728:≥
4712:∈
4626:≅
4541:−
4339:…
4327:α
4314:α
4301:α
4219:−
4200:∈
4092:−
4077:α
4071:∞
4056:∑
3985:−
3945:∖
3877:∪
3831:∪
3825:∈
3648:∈
3563:−
3491:−
3480:−
3427:−
3413:∞
3398:∑
3361:−
3347:−
3341:−
3320:−
3312:∞
3297:∑
3270:−
3249:∞
3234:∑
3143:∞
3128:∑
3099:−
3045:−
3039:−
3018:−
2989:−
2948:∞
2933:∑
2916:−
2895:−
2881:−
2837:−
2829:∞
2814:∑
2800:θ
2792:π
2780:∫
2771:−
2757:−
2713:−
2705:∞
2690:∑
2683:π
2661:θ
2653:θ
2644:−
2625:π
2613:∫
2604:−
2588:−
2574:−
2526:∑
2509:−
2501:∞
2486:∑
2479:π
2442:θ
2423:θ
2405:θ
2383:−
2369:−
2321:∑
2312:π
2300:∫
2283:−
2275:∞
2260:∑
2253:π
2216:θ
2197:θ
2179:θ
2159:−
2145:π
2133:∫
2116:−
2108:∞
2093:∑
2086:π
2043:θ
2024:θ
2016:θ
1986:−
1981:θ
1953:π
1941:∫
1924:−
1916:∞
1901:∑
1891:π
1847:−
1844:ζ
1836:ζ
1817:−
1814:ζ
1800:∂
1796:∫
1779:−
1771:∞
1756:∑
1746:π
1702:−
1699:ζ
1691:ζ
1672:−
1669:ζ
1650:−
1642:∞
1627:∑
1615:∂
1611:∫
1601:π
1557:−
1554:ζ
1546:ζ
1537:ζ
1520:∂
1516:∫
1506:π
1400:⊂
1394:∂
1391:∪
1365:∂
1285:ρ
1239:−
1228:−
1219:ρ
1196:∂
1130:∪
1002:−
981:∞
966:∑
925:∈
853:∂
850:∈
804:−
784:∂
747:−
668:−
646:−
638:∞
623:∑
273:connected
219:∈
213:∀
56:divergent
8778:(1979).
8685:See also
8434:lacunary
8155:Suppose
6687:for any
5532:, to be
5437:singular
5026:, hence
4643:topology
1415:. Using
485:and the
90:Suppose
8825:, 2001
8734:Bibcode
8671:around
8222:, then
5433:regular
4994:, is a
3699:, then
3617:around
1337:around
1265:. Take
698:By the
271:is the
105:of the
8440:) and
8200:domain
7448:where
7339:, let
6327:
6319:
5857:Since
5566:
5407:. See
4986:where
4669:. Let
4608:extend
4574:where
4388:, the
4367:. The
4029:. Let
4007:, the
3202:Then,
1297:; let
166:, and
94:is an
8357:with
8195:is a
8191:. If
7644:when
6258:when
5608:when
5409:sheaf
5382:)) =
5349:sheaf
5206:near
5050:is a
5000:atlas
4996:chart
4901:sheaf
4518:. If
4516:germs
4396:is (α
4357:is a
4127:be a
3663:with
519:into
386:then
240:then
8452:Let
8414:>
8119:>
7665:<
7132:>
7019:<
6712:<
6577:<
6405:>
6012:Sing
5710:<
5695:<
5628:>
5484:>
5464:For
5212:germ
5002:for
4770:<
4586:and
4559:<
4510:and
4506:Let
4422:is α
4390:stem
4369:base
4360:germ
4237:<
4133:disk
4022:germ
3684:>
1282:<
1276:<
1250:>
758:<
462:for
282:and
8742:doi
8730:119
8249:on
8218:in
5815:log
5758:as
4874:of
4645:on
4514:be
4459:, α
4455:, α
4448:= (
4434:at
4418:of
4410:top
4404:, α
4400:, α
4392:of
4381:is
4377:of
4363:of
4150:),
1211:is
1188:to
454:of
301:in
256:to
252:of
133:If
30:In
8861::
8843:.
8821:,
8815:,
8740:.
8728:.
8724:.
8444:.
8257:.
8230:.
8122:1.
8013::=
7370::=
7301:2.
7298::=
7135:1.
7022:1.
6580:1.
6525::=
6021::=
5952::=
5897::=
5555::=
5503:,
5456:.
5082:.
5054:.
4870:A
4867:.
4638:.
4602:≥
4498:.
4441:.
1165:.
940::
868:.
597::
523:.
504:.
489:.
466:.
131:.
74:.
58:.
38:,
8849:.
8766:.
8748:.
8744::
8736::
8676:0
8673:z
8669:f
8650:k
8646:)
8640:0
8636:z
8629:z
8626:(
8621:k
8611:k
8596:0
8593:=
8590:k
8582:=
8579:)
8576:z
8573:(
8570:f
8556:k
8552:ε
8533:k
8529:)
8523:0
8519:z
8512:z
8509:(
8504:k
8489:0
8486:=
8483:k
8475:=
8472:)
8469:z
8466:(
8463:f
8417:1
8407:k
8403:n
8397:1
8394:+
8391:k
8387:n
8373:k
8338:k
8334:n
8329:z
8323:k
8319:a
8308:0
8305:=
8302:k
8294:=
8291:)
8288:z
8285:(
8282:f
8255:S
8251:G
8247:f
8243:G
8239:S
8235:G
8228:G
8224:f
8220:D
8216:a
8212:G
8208:f
8204:D
8193:G
8189:D
8185:f
8170:C
8163:D
8116:c
8111:Z
8104:c
8084:)
8081:z
8078:(
8073:c
8067:L
8044:}
8041:1
8038:=
8034:|
8030:z
8026:|
8022::
8019:z
8016:{
8008:1
8004:C
7980:=
7977:)
7974:z
7971:(
7966:c
7960:L
7947:z
7930:.
7924:+
7921:=
7918:)
7915:1
7912:(
7907:c
7901:L
7895:+
7888:i
7884:c
7879:z
7873:1
7865:n
7861:c
7855:0
7852:=
7849:i
7841:=
7838:)
7831:n
7827:c
7822:z
7818:(
7813:c
7807:L
7801:+
7794:i
7790:c
7785:z
7779:1
7771:n
7767:c
7761:0
7758:=
7755:i
7747:=
7744:)
7741:z
7738:(
7733:c
7727:L
7720:,
7715:n
7712:,
7709:c
7703:R
7694:z
7668:1
7661:|
7657:z
7653:|
7632:)
7629:z
7626:(
7621:c
7615:L
7592:1
7589:=
7582:n
7578:c
7573:z
7562:z
7543:n
7539:c
7516:n
7512:c
7508:=
7504:|
7498:n
7495:,
7492:c
7486:R
7479:|
7457:D
7433:,
7429:}
7425:1
7422:=
7415:n
7411:c
7406:z
7402::
7397:D
7385:D
7378:z
7374:{
7365:n
7362:,
7359:c
7353:R
7327:1
7321:n
7295:c
7282:z
7268:)
7265:z
7262:(
7257:c
7251:L
7226:n
7222:c
7201:)
7198:z
7195:(
7190:c
7184:L
7161:1
7155:n
7128:|
7124:z
7120:|
7109:z
7095:)
7092:z
7089:(
7084:c
7078:L
7055:1
7052:=
7049:z
7039:c
7015:|
7011:z
7007:|
7000:,
6997:)
6990:m
6986:c
6981:z
6977:(
6972:c
6966:L
6960:+
6953:i
6949:c
6944:z
6938:1
6932:m
6927:0
6924:=
6921:i
6913:=
6910:)
6907:z
6904:(
6899:c
6893:L
6867:)
6864:z
6861:(
6856:c
6850:L
6827:1
6821:m
6801:)
6796:c
6792:z
6788:(
6783:c
6777:L
6771:+
6766:c
6762:z
6758:=
6755:)
6752:z
6749:(
6744:c
6738:L
6715:1
6708:|
6704:z
6700:|
6689:z
6675:)
6672:z
6669:(
6664:c
6658:L
6633:n
6629:c
6622:c
6619:=
6614:1
6611:+
6608:n
6604:c
6573:|
6569:z
6565:|
6561:,
6554:n
6550:c
6545:z
6539:1
6533:n
6522:)
6519:z
6516:(
6511:c
6505:L
6489:c
6471:2
6465:c
6437:)
6434:s
6431:(
6428:P
6408:0
6402:C
6380:F
6376:I
6369:s
6363:,
6360:)
6357:C
6354:,
6351:C
6345:(
6339:)
6336:s
6333:(
6315:C
6306:F
6302:I
6281:)
6278:s
6275:(
6266:0
6246:)
6243:s
6240:(
6237:P
6227:s
6213:)
6210:s
6207:(
6204:P
6184:)
6181:s
6178:(
6175:P
6149:k
6125:}
6118:,
6113:4
6110:1
6105:,
6100:3
6097:1
6092:,
6087:2
6084:1
6079:,
6076:1
6072:{
6068:=
6064:}
6058:+
6053:Z
6045:k
6042::
6037:1
6030:k
6025:{
6016:P
5986:+
5981:Z
5973:k
5967:,
5961:k
5958:1
5949:s
5929:)
5926:s
5923:(
5920:P
5900:1
5894:s
5874:)
5871:s
5868:(
5842:.
5837:n
5833:)
5830:s
5827:n
5824:(
5809:)
5806:n
5803:(
5795:1
5789:n
5781:=
5778:)
5775:s
5772:(
5769:P
5742:)
5739:s
5736:(
5733:P
5713:1
5707:)
5704:s
5701:(
5692:0
5682:s
5660:)
5657:s
5654:(
5631:1
5625:)
5622:s
5619:(
5589:.
5584:s
5577:p
5563:p
5552:)
5549:s
5546:(
5543:P
5520:)
5517:s
5514:(
5511:P
5487:1
5481:)
5478:s
5475:(
5448:f
5429:f
5425:f
5421:r
5396:S
5392:S
5384:z
5380:z
5378:(
5376:f
5372:z
5370:(
5368:f
5364:S
5360:g
5352:S
5331:)
5324:,
5319:6
5316:1
5308:,
5303:5
5300:1
5295:,
5290:4
5287:1
5279:,
5274:3
5271:1
5266:,
5261:2
5258:1
5250:,
5247:1
5244:,
5241:0
5238:,
5235:1
5231:(
5227:=
5224:g
5208:z
5185:k
5181:)
5177:1
5171:z
5168:(
5163:k
5157:1
5154:+
5151:k
5147:)
5143:1
5137:(
5124:1
5121:=
5118:k
5110:=
5107:)
5104:z
5101:(
5098:L
5064:G
5036:G
5012:G
4992:g
4988:r
4974:,
4970:C
4963:)
4960:g
4957:(
4952:r
4948:U
4944::
4939:0
4935:h
4931:=
4928:)
4925:h
4922:(
4917:g
4884:G
4853:G
4825:G
4817:g
4807:r
4803:g
4801:(
4798:r
4796:U
4779:.
4776:}
4773:r
4766:|
4760:0
4756:h
4747:0
4743:g
4738:|
4734:,
4731:h
4725:g
4722::
4717:G
4709:h
4706:{
4703:=
4700:)
4697:g
4694:(
4689:r
4685:U
4671:r
4655:G
4604:h
4600:g
4596:g
4592:h
4588:h
4584:g
4580:g
4576:r
4562:r
4555:|
4549:0
4545:g
4536:0
4532:h
4527:|
4512:h
4508:g
4484:G
4472:r
4468:0
4465:z
4461:1
4457:0
4453:0
4450:z
4446:g
4439:0
4436:z
4432:f
4428:g
4424:0
4420:g
4416:1
4413:g
4406:2
4402:1
4398:0
4394:g
4386:0
4383:z
4379:g
4375:0
4372:g
4365:f
4342:)
4336:,
4331:2
4323:,
4318:1
4310:,
4305:0
4297:,
4292:0
4288:z
4284:(
4281:=
4278:g
4265:r
4261:r
4255:.
4243:}
4240:r
4233:|
4227:0
4223:z
4216:z
4212:|
4208::
4204:C
4197:z
4194:{
4191:=
4188:)
4183:0
4179:z
4175:(
4170:r
4166:D
4152:r
4148:0
4145:z
4143:(
4140:r
4136:D
4110:k
4106:)
4100:0
4096:z
4089:z
4086:(
4081:k
4066:0
4063:=
4060:k
4052:=
4049:)
4046:z
4043:(
4040:f
3991:)
3988:1
3982:(
3979:f
3957:.
3954:}
3951:0
3948:{
3941:C
3920:f
3900:f
3880:V
3874:U
3854:b
3834:V
3828:U
3822:b
3800:.
3797:)
3794:i
3791:+
3788:3
3785:(
3779:2
3776:1
3770:=
3767:a
3747:U
3727:U
3707:V
3687:1
3680:|
3676:a
3672:|
3651:U
3645:a
3625:0
3604:|
3600:a
3596:|
3566:a
3560:)
3557:a
3554:+
3551:z
3548:(
3544:1
3539:=
3527:z
3524:1
3519:=
3505:)
3499:a
3496:z
3488:1
3484:(
3477:1
3473:1
3466:a
3463:1
3458:=
3446:k
3441:)
3435:a
3432:z
3424:1
3420:(
3408:0
3405:=
3402:k
3392:a
3389:1
3384:=
3372:k
3368:)
3364:a
3358:z
3355:(
3350:1
3344:k
3337:a
3331:k
3327:)
3323:1
3317:(
3307:0
3304:=
3301:k
3293:=
3281:k
3277:)
3273:a
3267:z
3264:(
3259:k
3255:a
3244:0
3241:=
3238:k
3230:=
3223:)
3220:z
3217:(
3214:f
3188:.
3183:m
3179:x
3172:)
3167:k
3163:k
3160:+
3157:m
3151:(
3138:0
3135:=
3132:m
3124:=
3116:1
3113:+
3110:k
3106:)
3102:x
3096:1
3093:(
3089:1
3073:k
3057:.
3048:1
3042:k
3035:a
3029:k
3025:)
3021:1
3015:(
3012:=
3000:m
2996:)
2992:a
2986:1
2983:(
2977:)
2972:k
2968:k
2965:+
2962:m
2956:(
2943:0
2940:=
2937:m
2927:k
2923:)
2919:1
2913:(
2910:=
2898:k
2892:n
2888:)
2884:1
2878:a
2875:(
2869:)
2864:k
2861:n
2856:(
2848:n
2844:)
2840:1
2834:(
2824:k
2821:=
2818:n
2810:=
2797:d
2789:2
2784:0
2774:k
2768:n
2764:)
2760:1
2754:a
2751:(
2745:)
2740:k
2737:n
2732:(
2724:n
2720:)
2716:1
2710:(
2700:k
2697:=
2694:n
2680:2
2676:1
2671:=
2658:d
2650:)
2647:k
2641:m
2638:(
2635:i
2631:e
2622:2
2617:0
2607:k
2601:m
2597:r
2591:m
2585:n
2581:)
2577:1
2571:a
2568:(
2562:)
2557:m
2554:n
2549:(
2541:n
2536:0
2533:=
2530:m
2520:n
2516:)
2512:1
2506:(
2496:0
2493:=
2490:n
2476:2
2472:1
2467:=
2452:k
2448:)
2439:i
2435:e
2431:r
2428:(
2420:d
2415:m
2411:)
2402:i
2398:e
2394:r
2391:(
2386:m
2380:n
2376:)
2372:1
2366:a
2363:(
2357:)
2352:m
2349:n
2344:(
2336:n
2331:0
2328:=
2325:m
2309:2
2304:0
2294:n
2290:)
2286:1
2280:(
2270:0
2267:=
2264:n
2250:2
2246:1
2241:=
2226:k
2222:)
2213:i
2209:e
2205:r
2202:(
2194:d
2189:n
2185:)
2176:i
2172:e
2168:r
2165:+
2162:1
2156:a
2153:(
2142:2
2137:0
2127:n
2123:)
2119:1
2113:(
2103:0
2100:=
2097:n
2083:2
2079:1
2074:=
2059:1
2056:+
2053:k
2049:)
2040:i
2036:e
2032:r
2029:(
2021:d
2013:i
2009:e
2005:i
2002:r
1997:n
1993:)
1989:1
1978:i
1974:e
1970:r
1967:+
1964:a
1961:(
1950:2
1945:0
1935:n
1931:)
1927:1
1921:(
1911:0
1908:=
1905:n
1894:i
1888:2
1884:1
1879:=
1864:1
1861:+
1858:k
1854:)
1850:a
1841:(
1833:d
1828:n
1824:)
1820:1
1811:(
1803:D
1790:n
1786:)
1782:1
1776:(
1766:0
1763:=
1760:n
1749:i
1743:2
1739:1
1734:=
1719:1
1716:+
1713:k
1709:)
1705:a
1696:(
1688:d
1683:n
1679:)
1675:1
1666:(
1661:n
1657:)
1653:1
1647:(
1637:0
1634:=
1631:n
1618:D
1604:i
1598:2
1594:1
1589:=
1574:1
1571:+
1568:k
1564:)
1560:a
1551:(
1543:d
1540:)
1534:(
1531:f
1523:D
1509:i
1503:2
1499:1
1494:=
1481:!
1478:k
1473:)
1470:a
1467:(
1462:)
1459:k
1456:(
1452:f
1445:=
1436:k
1432:a
1403:U
1397:D
1388:D
1368:D
1345:a
1325:r
1305:D
1279:r
1273:0
1253:0
1246:|
1242:1
1236:a
1232:|
1225:1
1222:=
1199:U
1176:a
1153:U
1133:V
1127:U
1107:f
1087:U
1067:V
1045:k
1041:a
1018:.
1013:k
1009:)
1005:a
999:z
996:(
991:k
987:a
976:0
973:=
970:k
962:=
959:)
956:z
953:(
950:f
928:U
922:a
902:z
898:/
894:1
891:=
888:)
885:z
882:(
879:f
856:U
847:0
844:=
841:z
821:}
818:1
815:=
811:|
807:1
801:z
797:|
793:{
790:=
787:U
764:}
761:1
754:|
750:1
744:z
740:|
736:{
733:=
730:U
710:f
684:.
679:k
675:)
671:1
665:z
662:(
657:k
653:)
649:1
643:(
633:0
630:=
627:k
619:=
616:)
613:z
610:(
607:f
585:1
582:=
579:z
555:f
541:V
537:U
456:f
452:U
448:2
445:F
441:1
438:F
434:V
415:2
411:F
407:=
402:1
398:F
371:,
368:)
365:z
362:(
359:f
356:=
353:)
350:z
347:(
342:2
338:F
334:=
331:)
328:z
325:(
320:1
316:F
303:U
299:z
295:V
291:U
287:2
284:F
280:1
277:F
269:V
262:f
258:U
254:F
246:f
242:F
225:,
222:U
216:z
209:)
206:z
203:(
200:f
197:=
194:)
191:z
188:(
185:F
172:V
168:F
164:U
160:,
147:C
135:V
118:C
103:U
92:f
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.