17:
29:
161:
showed in 1878. Cantor's result came as a surprise to many mathematicians and kicked off the line of research leading to space-filling curves, Osgood curves, and Netto's theorem. A near-bijection from the unit square to the unit interval can be obtained by interleaving the digits of the decimal
238:
and a two-dimensional set, see
Section 6.4, "Proof of Netto's Theorem", pp. 97–98. For the application of Netto's theorem to self-intersections of space-filling curves, and for Osgood curves, see Chapter 8, "Jordan Curves of Positive Lebesgue Measure", pp.
120:
from one-dimensional spaces to two-dimensional spaces. They cover every point of the plane, or of a unit square, by the image of a line or unit interval. Examples include the
109:. The conditions of the theorem can be relaxed in different ways to obtain interesting classes of functions from one-dimensional spaces to two-dimensional spaces:
128:. Neither of these examples has any self-crossings, but by Netto's theorem there are many points of the square that are covered multiple times by these curves.
234:. For the statement of the theorem, and historical background, see Theorem 1.3, p. 6. For its proof for the case of bijections between the
93:
An important special case of this theorem concerns the non-existence of continuous bijections from one-dimensional spaces, such as the
175:
299:
220:
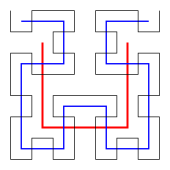
36:, with no self-intersections. By Netto's theorem it is impossible for such a curve to entirely cover any two-dimensional region.
63:. That is, there does not exist a continuous bijection between two smooth manifolds of different dimension. It is named after
143:
352:
154:
254:
Dauben, Joseph W. (1975), "The invariance of dimension: problems in the early development of set theory and topology",
75:
347:
166:
of points in the square. The ambiguities of decimal, exemplified by the two decimal representations of 1 =
142:
in the plane. However, by Netto's theorem, they cannot cover the entire plane, unit square, or any other
149:
If one relaxes the requirement of continuity, then all smooth manifolds of bounded dimension have equal
41:
163:
320:
90:
in 1879, gave faulty proofs of the general theorem. The faults were later recognized and corrected.
117:
113:
49:
316:
171:
70:
The case for maps from a higher-dimensional manifold to a one-dimensional manifold was proven by
134:
are continuous bijections from one-dimensional spaces to subsets of the plane that have nonzero
216:
308:
263:
208:
328:
277:
230:
324:
273:
226:
102:
56:
312:
71:
341:
268:
235:
125:
98:
21:
158:
139:
131:
87:
33:
150:
121:
106:
64:
212:
157:. Therefore, there exist discontinuous bijections between any two of them, as
16:
94:
83:
60:
52:
294:
24:, a space-filling curve that by Netto's theorem has many self-intersections
28:
167:
202:
174:
rather than a bijection, but this issue can be repaired by using the
79:
27:
15:
135:
82:can be mapped continuously and bijectively to the
78:to show that no manifold containing a topological
20:The first three steps of construction of the
8:
207:, Universitext, New York: Springer-Verlag,
267:
101:, to two-dimensional spaces, such as the
288:
286:
249:
247:
245:
196:
194:
192:
188:
7:
321:10.4169/amer.math.monthly.118.03.198
313:10.4169/amer.math.monthly.118.03.198
14:
300:The American Mathematical Monthly
118:surjective continuous functions
1:
293:Gouvêa, Fernando Q. (2011),
269:10.1016/0315-0860(75)90066-X
155:cardinality of the continuum
369:
176:Schröder–Bernstein theorem
86:. Both Netto in 1878, and
76:intermediate value theorem
213:10.1007/978-1-4612-0871-6
295:"Was Cantor surprised?"
162:representations of the
170:, cause this to be an
144:two-dimensional region
37:
25:
164:Cartesian coordinates
42:mathematical analysis
31:
19:
353:Theorems in topology
256:Historia Mathematica
204:Space-filling curves
201:Sagan, Hans (1994),
114:Space-filling curves
74:in 1878, using the
38:
26:
360:
348:Dimension theory
332:
331:
290:
281:
280:
271:
251:
240:
233:
198:
57:smooth manifolds
368:
367:
363:
362:
361:
359:
358:
357:
338:
337:
336:
335:
292:
291:
284:
253:
252:
243:
223:
200:
199:
190:
185:
103:Euclidean plane
46:Netto's theorem
12:
11:
5:
366:
364:
356:
355:
350:
340:
339:
334:
333:
307:(3): 198–209,
282:
241:
221:
187:
186:
184:
181:
180:
179:
147:
129:
13:
10:
9:
6:
4:
3:
2:
365:
354:
351:
349:
346:
345:
343:
330:
326:
322:
318:
314:
310:
306:
302:
301:
296:
289:
287:
283:
279:
275:
270:
265:
261:
257:
250:
248:
246:
242:
237:
236:unit interval
232:
228:
224:
222:0-387-94265-3
218:
214:
210:
206:
205:
197:
195:
193:
189:
182:
177:
173:
169:
165:
160:
156:
152:
148:
145:
141:
140:Jordan curves
137:
133:
132:Osgood curves
130:
127:
126:Hilbert curve
123:
119:
115:
112:
111:
110:
108:
104:
100:
99:unit interval
96:
91:
89:
85:
81:
77:
73:
68:
66:
62:
58:
54:
51:
47:
43:
35:
30:
23:
22:Hilbert curve
18:
304:
298:
259:
255:
203:
159:Georg Cantor
138:. They form
92:
88:Georg Cantor
72:Jacob Lüroth
69:
48:states that
45:
39:
34:Osgood curve
262:: 273–288,
151:cardinality
122:Peano curve
107:unit square
65:Eugen Netto
342:Categories
183:References
53:bijections
50:continuous
172:injection
95:real line
84:real line
61:dimension
59:preserve
239:131–143.
168:0.999...
329:2800330
278:0476319
231:1299533
327:
319:
276:
229:
219:
153:, the
80:circle
317:JSTOR
217:ISBN
136:area
124:and
116:are
309:doi
305:118
264:doi
209:doi
105:or
97:or
55:of
40:In
32:An
344::
325:MR
323:,
315:,
303:,
297:,
285:^
274:MR
272:,
258:,
244:^
227:MR
225:,
215:,
191:^
67:.
44:,
311::
266::
260:2
211::
178:.
146:.
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.