1889:
1245:
1884:{\displaystyle {\begin{aligned}\sum _{k=1}^{n}k^{3}&=1+8+27+64+\cdots +n^{3}\\&=\underbrace {1} _{1^{3}}+\underbrace {3+5} _{2^{3}}+\underbrace {7+9+11} _{3^{3}}+\underbrace {13+15+17+19} _{4^{3}}+\cdots +\underbrace {\left(n^{2}-n+1\right)+\cdots +\left(n^{2}+n-1\right)} _{n^{3}}\\&=\underbrace {\underbrace {\underbrace {\underbrace {1} _{1^{2}}+3} _{2^{2}}+5} _{3^{2}}+\cdots +\left(n^{2}+n-1\right)} _{\left({\frac {n^{2}+n}{2}}\right)^{2}}\\&=(1+2+\cdots +n)^{2}\\&=\left(\sum _{k=1}^{n}k\right)^{2}.\end{aligned}}}
544:
38:
4938:
1916:
1038:
809:
of these two triangles, so its size is the square of a triangular number on the right hand side of the
Nichomachus identity. The probabilities themselves are respectively the left and right sides of the Nichomachus identity, normalized to make probabilities by dividing both sides
343:, pointed out that if one writes a list of the odd numbers, the first is the cube of 1, the sum of the next two is the cube of 2, the sum of the next three is the cube of 3, and so on. He does not go further than this, but from this it follows that the sum of the first
834:
195:
300:
2117:
1150:
1250:
2452:
637:
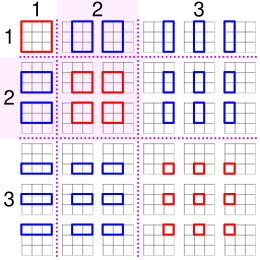
grid (or a square made up of three smaller squares on a side) can form 36 different rectangles. The number of squares in a square grid is similarly counted by the square pyramidal numbers.
1240:
1908:
times a triangular number, from which it follows that the sum of all the rows is the square of a triangular number. Alternatively, one can decompose the table into a sequence of nested
1912:, each consisting of the products in which the larger of the two terms is some fixed value. The sum within each gmonon is a cube, so the sum of the whole table is a sum of cubes.
1033:{\displaystyle n^{3}=\underbrace {\left(n^{2}-n+1\right)+\left(n^{2}-n+1+2\right)+\left(n^{2}-n+1+4\right)+\cdots +\left(n^{2}+n-1\right)} _{n{\text{ consecutive odd numbers}}}.}
3040:
45:. The nth coloured region shows n squares of dimension n by n (the rectangle is 1 evenly divided square), hence the area of the nth region is n times n x n.
2675:
2584:
78:
2011:
831:) gives a particularly simple derivation, by expanding each cube in the sum into a set of consecutive odd numbers. He begins by giving the identity
3033:
1057:
2524:
2360:
210:
1985:
study polynomial analogues of the square triangular number formula, in which series of polynomials add to the square of another polynomial.
2386:
3840:
3026:
2644:
2544:
2277:
3835:
1971:, of which the sum of cubes is the simplest and most elegant example. However, in no other case is one power sum a square of another.
3850:
3830:
1173:
41:
A square whose side length is a triangular number can be partitioned into squares and half-squares whose areas add to cubes. From
4543:
4123:
2050:
3845:
2668:
4629:
4972:
3945:
4977:
4295:
3614:
3407:
2853:
2403:
4330:
4300:
3975:
3965:
4471:
3885:
3619:
3599:
2858:
2838:
2171:
2126:
4161:
4325:
4967:
4420:
4043:
3800:
3609:
3591:
3485:
3475:
3465:
2848:
2830:
2729:
2719:
2709:
805:
form isosceles right triangles, and the set counted by the right hand side of the equation of probabilities is the
4305:
4548:
4093:
3500:
3495:
3490:
3480:
3457:
2744:
2739:
2734:
2724:
2701:
2661:
1935:
uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity (see also
3533:
2223:
31:
3790:
2320:
Kanim, Katherine (2004), "Proofs without words: The sum of cubes—An extension of
Archimedes' sum of squares",
4659:
4624:
4410:
4320:
4194:
4169:
4078:
4068:
3680:
3662:
3582:
2919:
2896:
2821:
620:
observes, these numbers also count the number of rectangles with horizontal and vertical sides formed in an
610:
556:
1967:, namely that odd power sums (sums of odd powers) are a polynomial in triangular numbers. These are called
4962:
4919:
4189:
4063:
3694:
3470:
3250:
3177:
2933:
2714:
2491:
1968:
1964:
306:
2392:
4174:
4028:
3955:
3110:
2988:
4883:
4523:
1977:
studies more general conditions under which the sum of a consecutive sequence of cubes forms a square.
4816:
4710:
4674:
4415:
4138:
4118:
3935:
3604:
3392:
3364:
2843:
2593:
2456:
2322:
1939:); he observes that it may also be proved easily (but uninformatively) by induction, and states that
1897:
2309:
4538:
4402:
4397:
4365:
4128:
4103:
4098:
4073:
4003:
3999:
3930:
3820:
3652:
3448:
3417:
2886:
2692:
525:
4937:
4941:
4695:
4690:
4604:
4578:
4476:
4455:
4227:
4108:
4058:
3980:
3950:
3890:
3657:
3637:
3568:
3281:
2914:
2891:
2807:
2575:
2535:
2473:
2339:
2256:
2240:
2218:
2188:
2155:
2143:
2046:
2042:
1928:
1041:
824:
3825:
2268:
761:
is largest is a sum of cubes, the left hand side of the
Nichomachus identity. The sets of pairs
471:
claims that "every student of number theory surely must have marveled at this miraculous fact".
4835:
4780:
4634:
4609:
4583:
4360:
4038:
4033:
3960:
3940:
3925:
3647:
3629:
3548:
3538:
3523:
3301:
3286:
2881:
2868:
2787:
2777:
2767:
2624:
2520:
2356:
806:
606:
543:
69:
2641:
4871:
4664:
4250:
4222:
4212:
4204:
4088:
4053:
4048:
4015:
3709:
3672:
3563:
3558:
3553:
3543:
3515:
3402:
3354:
3349:
3306:
3245:
2948:
2906:
2802:
2797:
2792:
2782:
2759:
2601:
2553:
2465:
2370:
Pengelley, David (2002), "The bridge between continuous and discrete via original sources",
2331:
2286:
2232:
2180:
2135:
2567:
2504:
2300:
2252:
4847:
4736:
4669:
4595:
4518:
4492:
4310:
4023:
3880:
3815:
3785:
3775:
3770:
3436:
3344:
3291:
3135:
3075:
2684:
2648:
2563:
2500:
2296:
2248:
2163:
1909:
602:
2628:
2597:
4852:
4720:
4705:
4569:
4533:
4508:
4384:
4355:
4340:
4217:
4113:
4083:
3810:
3765:
3642:
3240:
3235:
3230:
3202:
3187:
3100:
3085:
3063:
3050:
2876:
2200:
2159:
630:
57:
2486:
37:
4956:
4775:
4759:
4700:
4654:
4350:
4335:
4245:
3970:
3528:
3397:
3359:
3316:
3197:
3182:
3172:
3130:
3120:
3095:
2998:
2772:
2512:
2260:
61:
50:
467:
Many early mathematicians have studied and provided proofs of
Nicomachus's theorem.
200:
The same equation may be written more compactly using the mathematical notation for
4811:
4800:
4715:
4553:
4528:
4445:
4345:
4315:
4290:
4274:
4179:
4146:
3895:
3869:
3780:
3719:
3296:
3192:
3125:
3105:
3080:
3003:
2958:
2204:
590:
1919:
Visual demonstration that the square of a triangular number equals a sum of cubes.
17:
190:{\displaystyle 1^{3}+2^{3}+3^{3}+\cdots +n^{3}=\left(1+2+3+\cdots +n\right)^{2}.}
4770:
4645:
4450:
3914:
3805:
3760:
3755:
3505:
3412:
3311:
3140:
3115:
3090:
2993:
2749:
2001:
640:
The identity also admits a natural probabilistic interpretation as follows. Let
586:
4907:
4888:
4184:
3795:
2371:
582:
578:
574:
514:
476:
314:
3018:
658:
be four integer numbers independently and uniformly chosen at random between
4513:
4440:
4432:
4237:
4151:
3269:
2973:
2633:
510:
492:
484:
201:
2606:
1915:
4614:
509:
mentions several additional early mathematical works on this formula, by
2379:, National Center for Mathematics Education, Univ. of Gothenburg, Sweden
2192:
4619:
4278:
2477:
2343:
2244:
2147:
295:{\displaystyle \sum _{k=1}^{n}k^{3}=\left(\sum _{k=1}^{n}k\right)^{2}.}
2184:
502:
480:
2579:
2469:
2335:
2236:
2139:
2653:
2558:
2291:
1914:
1170:. Applying this property, along with another well-known identity:
542:
488:
36:
4905:
4869:
4833:
4797:
4757:
4382:
4271:
3997:
3912:
3867:
3744:
3434:
3381:
3333:
3267:
3219:
3157:
3061:
3022:
2657:
670:
is the largest of the four numbers equals the probability that
2580:"On the formation of powers from arithmetical progressions"
2005:
539:
Numeric values; geometric and probabilistic interpretation
605:, a four-dimensional hyperpyramidal generalization of the
475:
finds references to the identity not only in the works of
2112:{\displaystyle \textstyle \sum k^{3}={n+1 \choose 2}^{2}}
1896:
obtains another proof by summing the numbers in a square
2487:"On the sum of consecutive cubes being a perfect square"
1145:{\displaystyle n^{3}=\sum _{k=T_{n-1}+1}^{T_{n}}(2k-1),}
1963:
A similar result to
Nicomachus's theorem holds for all
1158:
start off just after those forming all previous values
30:
For triangular numbers that are themselves square, see
2407:
2054:
2406:
2400:
Stein, Robert G. (1971), "A combinatorial proof that
2053:
1248:
1176:
1060:
837:
735:
so (adding the size of this cube over all choices of
213:
81:
4729:
4683:
4643:
4594:
4568:
4501:
4485:
4464:
4431:
4396:
4236:
4203:
4160:
4137:
4014:
3702:
3693:
3671:
3628:
3590:
3581:
3514:
3456:
3447:
2981:
2971:
2941:
2932:
2905:
2867:
2829:
2820:
2758:
2700:
2691:
535:, India); he reproduces Nilakantha's visual proof.
2447:{\displaystyle \textstyle \sum k^{3}=(\sum k)^{2}}
2446:
2111:
1936:
1883:
1234:
1144:
1032:
294:
189:
2308:Gulley, Ned (March 4, 2010), Shure, Loren (ed.),
2221:(1957), "Sums of powers of the natural numbers",
372:odd numbers, that is, the odd numbers from 1 to
1948:
2267:Garrett, Kristina C.; Hummel, Kristen (2004),
570:The sequence of squared triangular numbers is
3034:
2669:
2373:Study the Masters: The Abel-Fauvel Conference
2096:
2075:
1978:
596:441, 784, 1296, 2025, 3025, 4356, 6084, 8281,
8:
2206:Calculus before Newton and Leibniz, Part III
1943:provides "an interesting old Arabic proof".
1923:In the more recent mathematical literature,
1235:{\displaystyle n^{2}=\sum _{k=1}^{n}(2k-1),}
483:in the 1st century CE, but also in those of
383:. The average of these numbers is obviously
339:Nicomachus, at the end of Chapter 20 of his
4902:
4866:
4830:
4794:
4754:
4428:
4393:
4379:
4268:
4011:
3994:
3909:
3864:
3741:
3699:
3587:
3453:
3444:
3431:
3378:
3335:Possessing a specific set of other numbers
3330:
3264:
3216:
3154:
3058:
3041:
3027:
3019:
2978:
2938:
2826:
2697:
2676:
2662:
2654:
2585:Proceedings of the Royal Society of London
828:
2605:
2557:
2437:
2415:
2405:
2290:
2102:
2095:
2074:
2072:
2062:
2052:
2012:On-Line Encyclopedia of Integer Sequences
1868:
1854:
1843:
1817:
1771:
1749:
1742:
1736:
1707:
1681:
1676:
1656:
1651:
1631:
1626:
1616:
1612:
1608:
1604:
1585:
1580:
1551:
1510:
1498:
1480:
1475:
1445:
1433:
1428:
1404:
1392:
1387:
1369:
1357:
1352:
1342:
1325:
1278:
1268:
1257:
1249:
1247:
1205:
1194:
1181:
1175:
1113:
1108:
1089:
1078:
1065:
1059:
1020:
1016:
987:
940:
899:
864:
852:
842:
836:
472:
283:
269:
258:
239:
229:
218:
212:
178:
131:
112:
99:
86:
80:
1974:
1940:
506:
468:
2025:
1993:
1982:
1924:
2642:A visual proof of Nicomachus's theorem
2164:"Summing cubes by counting rectangles"
1952:
1900:in two different ways. The sum of the
42:
2269:"A combinatorial proof of the sum of
1944:
1932:
617:
7:
2388:Geometric Exercises in Paper Folding
491:in the 5th century, and in those of
2545:Electronic Journal of Combinatorics
2278:Electronic Journal of Combinatorics
2047:"Two quick combinatorial proofs of
1951:provide two additional proofs, and
1893:
1242:produces the following derivation:
563:(red), in a 3 × 3 square
2079:
347:cubes equals the sum of the first
25:
4936:
4544:Perfect digit-to-digit invariant
2517:The Calculus, a Genetic Approach
1947:provides a purely visual proof,
1937:Benjamin, Quinn & Wurtz 2006
739:) the number of combinations of
633:. For instance, the points of a
2519:, University of Chicago Press,
601:These numbers can be viewed as
2540:-analogue of the sum of cubes"
2434:
2424:
2355:, Cambridge University Press,
1955:gives seven geometric proofs.
1814:
1789:
1226:
1211:
1152:and thus the summands forming
1136:
1121:
696:. For any particular value of
1:
3383:Expressible via specific sums
2854:Centered dodecahedral numbers
1949:Benjamin & Orrison (2002)
1022: consecutive odd numbers
666:. Then, the probability that
565:(4 × 4 vertex) grid
529:
518:
495:
325:
318:
27:Square of a triangular number
2859:Centered icosahedral numbers
2839:Centered tetrahedral numbers
1040:That identity is related to
4472:Multiplicative digital root
2849:Centered octahedral numbers
2730:Centered heptagonal numbers
2720:Centered pentagonal numbers
2710:Centered triangular numbers
2172:College Mathematics Journal
2127:College Mathematics Journal
1979:Garrett & Hummel (2004)
4994:
2954:Squared triangular numbers
2745:Centered decagonal numbers
2740:Centered nonagonal numbers
2735:Centered octagonal numbers
2725:Centered hexagonal numbers
2002:Sloane, N. J. A.
341:Introduction to Arithmetic
29:
4932:
4915:
4901:
4879:
4865:
4843:
4829:
4807:
4793:
4766:
4753:
4549:Perfect digital invariant
4392:
4378:
4286:
4267:
4124:Superior highly composite
4010:
3993:
3921:
3908:
3876:
3863:
3751:
3740:
3443:
3430:
3388:
3377:
3340:
3329:
3277:
3263:
3226:
3215:
3168:
3153:
3071:
3057:
2351:Nelsen, Roger B. (1993),
2162:; Wurtz, Calyssa (2006),
2045:; Orrison, M. E. (2002),
433:of them, so their sum is
4162:Euler's totient function
3946:Euler–Jacobi pseudoprime
3221:Other polynomial numbers
2920:Square pyramidal numbers
2897:Stella octangula numbers
2534:Warnaar, S. Ole (2004),
2485:Stroeker, R. J. (1995),
2385:Row, T. Sundara (1893),
2224:The Mathematical Gazette
682:is at least as large as
674:is at least as large as
611:square pyramidal numbers
555:) rectangles, including
32:square triangular number
3976:Somer–Lucas pseudoprime
3966:Lucas–Carmichael number
3801:Lazy caterer's sequence
2715:Centered square numbers
2285:(1), Research Paper 9,
2006:"Sequence A000537"
1927:provides a proof using
513:(10th century Arabia),
53:, the sum of the first
3851:Wedderburn–Etherington
3251:Lucky numbers of Euler
2629:"Nicomachus's theorem"
2607:10.1098/rspl.1854.0036
2492:Compositio Mathematica
2448:
2113:
1920:
1885:
1859:
1273:
1236:
1210:
1146:
1120:
1054:in the following way:
1034:
825:Charles Wheatstone
700:, the combinations of
567:
296:
274:
234:
191:
46:
4139:Prime omega functions
3956:Frobenius pseudoprime
3746:Combinatorial numbers
3615:Centered dodecahedral
3408:Primary pseudoperfect
2844:Centered cube numbers
2449:
2114:
1969:Faulhaber polynomials
1918:
1886:
1839:
1253:
1237:
1190:
1147:
1074:
1035:
546:
297:
254:
214:
192:
40:
4973:Algebraic identities
4598:-composition related
4398:Arithmetic functions
4000:Arithmetic functions
3936:Elliptic pseudoprime
3620:Centered icosahedral
3600:Centered tetrahedral
2887:Dodecahedral numbers
2457:Mathematics Magazine
2404:
2353:Proofs without Words
2323:Mathematics Magazine
2311:Nicomachus's Theorem
2051:
1898:multiplication table
1246:
1174:
1058:
835:
716:largest form a cube
315:Nicomachus of Gerasa
311:Nicomachus's theorem
309:is sometimes called
211:
79:
4978:Proof without words
4524:Kaprekar's constant
4044:Colossally abundant
3931:Catalan pseudoprime
3831:Schröder–Hipparchus
3610:Centered octahedral
3486:Centered heptagonal
3476:Centered pentagonal
3466:Centered triangular
3066:and related numbers
3004:8-hypercube numbers
2999:7-hypercube numbers
2994:6-hypercube numbers
2989:5-hypercube numbers
2959:Tesseractic numbers
2915:Tetrahedral numbers
2892:Icosahedral numbers
2808:Dodecagonal numbers
2598:1854RSPS....7..145W
2391:, Madras: Addison,
2156:Benjamin, Arthur T.
2043:Benjamin, Arthur T.
526:Nilakantha Somayaji
4942:Mathematics portal
4884:Aronson's sequence
4630:Smarandache–Wellin
4387:-dependent numbers
4094:Primitive abundant
3981:Strong pseudoprime
3971:Perrin pseudoprime
3951:Fermat pseudoprime
3891:Wolstenholme prime
3715:Squared triangular
3501:Centered decagonal
3496:Centered nonagonal
3491:Centered octagonal
3481:Centered hexagonal
2882:Octahedral numbers
2788:Heptagonal numbers
2778:Pentagonal numbers
2768:Triangular numbers
2647:2019-10-19 at the
2625:Weisstein, Eric W.
2444:
2443:
2219:Edmonds, Sheila M.
2160:Quinn, Jennifer J.
2109:
2108:
1929:summation by parts
1921:
1881:
1879:
1778:
1734:
1688:
1674:
1663:
1649:
1638:
1624:
1592:
1578:
1487:
1473:
1440:
1426:
1399:
1385:
1364:
1350:
1232:
1142:
1042:triangular numbers
1030:
1026:
1014:
607:triangular numbers
568:
292:
187:
47:
18:Nicomachus theorem
4968:Integer sequences
4950:
4949:
4928:
4927:
4897:
4896:
4861:
4860:
4825:
4824:
4789:
4788:
4749:
4748:
4745:
4744:
4564:
4563:
4374:
4373:
4263:
4262:
4259:
4258:
4205:Aliquot sequences
4016:Divisor functions
3989:
3988:
3961:Lucas pseudoprime
3941:Euler pseudoprime
3926:Carmichael number
3904:
3903:
3859:
3858:
3736:
3735:
3732:
3731:
3728:
3727:
3689:
3688:
3577:
3576:
3534:Square triangular
3426:
3425:
3373:
3372:
3325:
3324:
3259:
3258:
3211:
3210:
3149:
3148:
3016:
3015:
3012:
3011:
2967:
2966:
2949:Pentatope numbers
2928:
2927:
2816:
2815:
2803:Decagonal numbers
2798:Nonagonal numbers
2793:Octagonal numbers
2783:Hexagonal numbers
2526:978-0-226-80667-9
2362:978-0-88385-700-7
2094:
2015:, OEIS Foundation
1765:
1617:
1615:
1613:
1611:
1609:
1607:
1605:
1603:
1499:
1497:
1446:
1444:
1405:
1403:
1370:
1368:
1343:
1341:
1023:
853:
851:
807:Cartesian product
70:triangular number
16:(Redirected from
4985:
4940:
4903:
4872:Natural language
4867:
4831:
4799:Generated via a
4795:
4755:
4660:Digit-reassembly
4625:Self-descriptive
4429:
4394:
4380:
4331:Lucas–Carmichael
4321:Harmonic divisor
4269:
4195:Sparsely totient
4170:Highly cototient
4079:Multiply perfect
4069:Highly composite
4012:
3995:
3910:
3865:
3846:Telephone number
3742:
3700:
3681:Square pyramidal
3663:Stella octangula
3588:
3454:
3445:
3437:Figurate numbers
3432:
3379:
3331:
3265:
3217:
3155:
3059:
3043:
3036:
3029:
3020:
2979:
2939:
2827:
2698:
2685:Figurate numbers
2678:
2671:
2664:
2655:
2638:
2637:
2610:
2609:
2570:
2561:
2539:
2529:
2507:
2499:(1–2): 295–307,
2480:
2453:
2451:
2450:
2445:
2442:
2441:
2420:
2419:
2395:
2380:
2378:
2365:
2346:
2315:
2314:, Matlab Central
2303:
2294:
2272:
2263:
2231:(337): 187–188,
2213:
2211:
2195:
2185:10.2307/27646391
2168:
2150:
2123:
2118:
2116:
2115:
2110:
2107:
2106:
2101:
2100:
2099:
2090:
2078:
2067:
2066:
2029:
2023:
2017:
2016:
1998:
1907:
1903:
1890:
1888:
1887:
1882:
1880:
1873:
1872:
1867:
1863:
1858:
1853:
1826:
1822:
1821:
1782:
1777:
1776:
1775:
1770:
1766:
1761:
1754:
1753:
1743:
1735:
1730:
1729:
1725:
1712:
1711:
1687:
1686:
1685:
1675:
1670:
1662:
1661:
1660:
1650:
1645:
1637:
1636:
1635:
1625:
1596:
1591:
1590:
1589:
1579:
1574:
1573:
1569:
1556:
1555:
1532:
1528:
1515:
1514:
1486:
1485:
1484:
1474:
1469:
1439:
1438:
1437:
1427:
1422:
1398:
1397:
1396:
1386:
1381:
1363:
1362:
1361:
1351:
1334:
1330:
1329:
1283:
1282:
1272:
1267:
1241:
1239:
1238:
1233:
1209:
1204:
1186:
1185:
1169:
1161:
1157:
1151:
1149:
1148:
1143:
1119:
1118:
1117:
1107:
1100:
1099:
1070:
1069:
1053:
1039:
1037:
1036:
1031:
1025:
1024:
1021:
1015:
1010:
1009:
1005:
992:
991:
968:
964:
945:
944:
927:
923:
904:
903:
886:
882:
869:
868:
847:
846:
815:
804:
794:
782:
772:
760:
756:
738:
734:
715:
711:
707:
703:
699:
695:
685:
681:
677:
673:
669:
665:
661:
657:
636:
629:
603:figurate numbers
597:
594:
566:
560:
554:
550:
534:
531:
523:
520:
500:
497:
473:Pengelley (2002)
463:
459:
457:
456:
453:
450:
432:
431:
429:
428:
425:
422:
408:, and there are
407:
406:
404:
403:
400:
397:
382:
371:
370:
368:
367:
364:
361:
346:
330:
327:
323:
320:
301:
299:
298:
293:
288:
287:
282:
278:
273:
268:
244:
243:
233:
228:
196:
194:
193:
188:
183:
182:
177:
173:
136:
135:
117:
116:
104:
103:
91:
90:
67:
56:
21:
4993:
4992:
4988:
4987:
4986:
4984:
4983:
4982:
4953:
4952:
4951:
4946:
4924:
4920:Strobogrammatic
4911:
4893:
4875:
4857:
4839:
4821:
4803:
4785:
4762:
4741:
4725:
4684:Divisor-related
4679:
4639:
4590:
4560:
4497:
4481:
4460:
4427:
4400:
4388:
4370:
4282:
4281:related numbers
4255:
4232:
4199:
4190:Perfect totient
4156:
4133:
4064:Highly abundant
4006:
3985:
3917:
3900:
3872:
3855:
3841:Stirling second
3747:
3724:
3685:
3667:
3624:
3573:
3510:
3471:Centered square
3439:
3422:
3384:
3369:
3336:
3321:
3273:
3272:defined numbers
3255:
3222:
3207:
3178:Double Mersenne
3164:
3145:
3067:
3053:
3051:natural numbers
3047:
3017:
3008:
2963:
2924:
2901:
2863:
2812:
2754:
2687:
2682:
2649:Wayback Machine
2623:
2622:
2619:
2614:
2574:
2537:
2533:
2527:
2511:
2484:
2470:10.2307/2688231
2433:
2411:
2402:
2401:
2399:
2384:
2376:
2369:
2363:
2350:
2336:10.2307/3219288
2319:
2307:
2270:
2266:
2237:10.2307/3609189
2217:
2209:
2201:Bressoud, David
2199:
2166:
2154:
2140:10.2307/1559017
2121:
2080:
2073:
2071:
2058:
2049:
2048:
2041:
2037:
2032:
2024:
2020:
2000:
1999:
1995:
1991:
1975:Stroeker (1995)
1961:
1959:Generalizations
1941:Toeplitz (1963)
1905:
1901:
1878:
1877:
1838:
1834:
1833:
1824:
1823:
1813:
1780:
1779:
1745:
1744:
1738:
1737:
1703:
1702:
1698:
1677:
1652:
1627:
1614:
1610:
1606:
1594:
1593:
1581:
1547:
1546:
1542:
1506:
1505:
1501:
1500:
1476:
1447:
1429:
1406:
1388:
1371:
1353:
1332:
1331:
1321:
1284:
1274:
1244:
1243:
1177:
1172:
1171:
1163:
1159:
1153:
1109:
1085:
1061:
1056:
1055:
1052:
1044:
983:
982:
978:
936:
935:
931:
895:
894:
890:
860:
859:
855:
854:
838:
833:
832:
822:
811:
796:
784:
774:
762:
758:
740:
736:
717:
713:
709:
705:
701:
697:
687:
683:
679:
675:
671:
667:
663:
659:
641:
634:
621:
599:
595:
573:
564:
558:
552:
548:
541:
532:
524:, France), and
521:
507:Bressoud (2004)
498:
479:in what is now
469:Stroeker (1995)
462:
454:
451:
441:
440:
438:
437:
434:
426:
423:
413:
412:
410:
409:
401:
398:
388:
387:
385:
384:
373:
365:
362:
352:
351:
349:
348:
344:
337:
328:
321:
253:
249:
248:
235:
209:
208:
145:
141:
140:
127:
108:
95:
82:
77:
76:
65:
54:
35:
28:
23:
22:
15:
12:
11:
5:
4991:
4989:
4981:
4980:
4975:
4970:
4965:
4955:
4954:
4948:
4947:
4945:
4944:
4933:
4930:
4929:
4926:
4925:
4923:
4922:
4916:
4913:
4912:
4906:
4899:
4898:
4895:
4894:
4892:
4891:
4886:
4880:
4877:
4876:
4870:
4863:
4862:
4859:
4858:
4856:
4855:
4853:Sorting number
4850:
4848:Pancake number
4844:
4841:
4840:
4834:
4827:
4826:
4823:
4822:
4820:
4819:
4814:
4808:
4805:
4804:
4798:
4791:
4790:
4787:
4786:
4784:
4783:
4778:
4773:
4767:
4764:
4763:
4760:Binary numbers
4758:
4751:
4750:
4747:
4746:
4743:
4742:
4740:
4739:
4733:
4731:
4727:
4726:
4724:
4723:
4718:
4713:
4708:
4703:
4698:
4693:
4687:
4685:
4681:
4680:
4678:
4677:
4672:
4667:
4662:
4657:
4651:
4649:
4641:
4640:
4638:
4637:
4632:
4627:
4622:
4617:
4612:
4607:
4601:
4599:
4592:
4591:
4589:
4588:
4587:
4586:
4575:
4573:
4570:P-adic numbers
4566:
4565:
4562:
4561:
4559:
4558:
4557:
4556:
4546:
4541:
4536:
4531:
4526:
4521:
4516:
4511:
4505:
4503:
4499:
4498:
4496:
4495:
4489:
4487:
4486:Coding-related
4483:
4482:
4480:
4479:
4474:
4468:
4466:
4462:
4461:
4459:
4458:
4453:
4448:
4443:
4437:
4435:
4426:
4425:
4424:
4423:
4421:Multiplicative
4418:
4407:
4405:
4390:
4389:
4385:Numeral system
4383:
4376:
4375:
4372:
4371:
4369:
4368:
4363:
4358:
4353:
4348:
4343:
4338:
4333:
4328:
4323:
4318:
4313:
4308:
4303:
4298:
4293:
4287:
4284:
4283:
4272:
4265:
4264:
4261:
4260:
4257:
4256:
4254:
4253:
4248:
4242:
4240:
4234:
4233:
4231:
4230:
4225:
4220:
4215:
4209:
4207:
4201:
4200:
4198:
4197:
4192:
4187:
4182:
4177:
4175:Highly totient
4172:
4166:
4164:
4158:
4157:
4155:
4154:
4149:
4143:
4141:
4135:
4134:
4132:
4131:
4126:
4121:
4116:
4111:
4106:
4101:
4096:
4091:
4086:
4081:
4076:
4071:
4066:
4061:
4056:
4051:
4046:
4041:
4036:
4031:
4029:Almost perfect
4026:
4020:
4018:
4008:
4007:
3998:
3991:
3990:
3987:
3986:
3984:
3983:
3978:
3973:
3968:
3963:
3958:
3953:
3948:
3943:
3938:
3933:
3928:
3922:
3919:
3918:
3913:
3906:
3905:
3902:
3901:
3899:
3898:
3893:
3888:
3883:
3877:
3874:
3873:
3868:
3861:
3860:
3857:
3856:
3854:
3853:
3848:
3843:
3838:
3836:Stirling first
3833:
3828:
3823:
3818:
3813:
3808:
3803:
3798:
3793:
3788:
3783:
3778:
3773:
3768:
3763:
3758:
3752:
3749:
3748:
3745:
3738:
3737:
3734:
3733:
3730:
3729:
3726:
3725:
3723:
3722:
3717:
3712:
3706:
3704:
3697:
3691:
3690:
3687:
3686:
3684:
3683:
3677:
3675:
3669:
3668:
3666:
3665:
3660:
3655:
3650:
3645:
3640:
3634:
3632:
3626:
3625:
3623:
3622:
3617:
3612:
3607:
3602:
3596:
3594:
3585:
3579:
3578:
3575:
3574:
3572:
3571:
3566:
3561:
3556:
3551:
3546:
3541:
3536:
3531:
3526:
3520:
3518:
3512:
3511:
3509:
3508:
3503:
3498:
3493:
3488:
3483:
3478:
3473:
3468:
3462:
3460:
3451:
3441:
3440:
3435:
3428:
3427:
3424:
3423:
3421:
3420:
3415:
3410:
3405:
3400:
3395:
3389:
3386:
3385:
3382:
3375:
3374:
3371:
3370:
3368:
3367:
3362:
3357:
3352:
3347:
3341:
3338:
3337:
3334:
3327:
3326:
3323:
3322:
3320:
3319:
3314:
3309:
3304:
3299:
3294:
3289:
3284:
3278:
3275:
3274:
3268:
3261:
3260:
3257:
3256:
3254:
3253:
3248:
3243:
3238:
3233:
3227:
3224:
3223:
3220:
3213:
3212:
3209:
3208:
3206:
3205:
3200:
3195:
3190:
3185:
3180:
3175:
3169:
3166:
3165:
3158:
3151:
3150:
3147:
3146:
3144:
3143:
3138:
3133:
3128:
3123:
3118:
3113:
3108:
3103:
3098:
3093:
3088:
3083:
3078:
3072:
3069:
3068:
3062:
3055:
3054:
3048:
3046:
3045:
3038:
3031:
3023:
3014:
3013:
3010:
3009:
3007:
3006:
3001:
2996:
2991:
2985:
2983:
2976:
2969:
2968:
2965:
2964:
2962:
2961:
2956:
2951:
2945:
2943:
2936:
2930:
2929:
2926:
2925:
2923:
2922:
2917:
2911:
2909:
2903:
2902:
2900:
2899:
2894:
2889:
2884:
2879:
2873:
2871:
2865:
2864:
2862:
2861:
2856:
2851:
2846:
2841:
2835:
2833:
2824:
2818:
2817:
2814:
2813:
2811:
2810:
2805:
2800:
2795:
2790:
2785:
2780:
2775:
2773:Square numbers
2770:
2764:
2762:
2756:
2755:
2753:
2752:
2747:
2742:
2737:
2732:
2727:
2722:
2717:
2712:
2706:
2704:
2695:
2689:
2688:
2683:
2681:
2680:
2673:
2666:
2658:
2652:
2651:
2639:
2618:
2617:External links
2615:
2613:
2612:
2576:Wheatstone, C.
2572:
2552:(1), Note 13,
2531:
2525:
2513:Toeplitz, Otto
2509:
2482:
2464:(3): 161–162,
2440:
2436:
2432:
2429:
2426:
2423:
2418:
2414:
2410:
2397:
2382:
2367:
2361:
2348:
2330:(4): 298–299,
2317:
2305:
2264:
2215:
2197:
2179:(5): 387–389,
2152:
2134:(5): 406–408,
2105:
2098:
2093:
2089:
2086:
2083:
2077:
2070:
2065:
2061:
2057:
2038:
2036:
2033:
2031:
2030:
2026:Edmonds (1957)
2018:
1992:
1990:
1987:
1983:Warnaar (2004)
1960:
1957:
1925:Edmonds (1957)
1876:
1871:
1866:
1862:
1857:
1852:
1849:
1846:
1842:
1837:
1832:
1829:
1827:
1825:
1820:
1816:
1812:
1809:
1806:
1803:
1800:
1797:
1794:
1791:
1788:
1785:
1783:
1781:
1774:
1769:
1764:
1760:
1757:
1752:
1748:
1741:
1733:
1728:
1724:
1721:
1718:
1715:
1710:
1706:
1701:
1697:
1694:
1691:
1684:
1680:
1673:
1669:
1666:
1659:
1655:
1648:
1644:
1641:
1634:
1630:
1623:
1620:
1602:
1599:
1597:
1595:
1588:
1584:
1577:
1572:
1568:
1565:
1562:
1559:
1554:
1550:
1545:
1541:
1538:
1535:
1531:
1527:
1524:
1521:
1518:
1513:
1509:
1504:
1496:
1493:
1490:
1483:
1479:
1472:
1468:
1465:
1462:
1459:
1456:
1453:
1450:
1443:
1436:
1432:
1425:
1421:
1418:
1415:
1412:
1409:
1402:
1395:
1391:
1384:
1380:
1377:
1374:
1367:
1360:
1356:
1349:
1346:
1340:
1337:
1335:
1333:
1328:
1324:
1320:
1317:
1314:
1311:
1308:
1305:
1302:
1299:
1296:
1293:
1290:
1287:
1285:
1281:
1277:
1271:
1266:
1263:
1260:
1256:
1252:
1251:
1231:
1228:
1225:
1222:
1219:
1216:
1213:
1208:
1203:
1200:
1197:
1193:
1189:
1184:
1180:
1141:
1138:
1135:
1132:
1129:
1126:
1123:
1116:
1112:
1106:
1103:
1098:
1095:
1092:
1088:
1084:
1081:
1077:
1073:
1068:
1064:
1048:
1029:
1019:
1013:
1008:
1004:
1001:
998:
995:
990:
986:
981:
977:
974:
971:
967:
963:
960:
957:
954:
951:
948:
943:
939:
934:
930:
926:
922:
919:
916:
913:
910:
907:
902:
898:
893:
889:
885:
881:
878:
875:
872:
867:
863:
858:
850:
845:
841:
821:
818:
572:
540:
537:
460:
435:
336:
333:
303:
302:
291:
286:
281:
277:
272:
267:
264:
261:
257:
252:
247:
242:
238:
232:
227:
224:
221:
217:
198:
197:
186:
181:
176:
172:
169:
166:
163:
160:
157:
154:
151:
148:
144:
139:
134:
130:
126:
123:
120:
115:
111:
107:
102:
98:
94:
89:
85:
26:
24:
14:
13:
10:
9:
6:
4:
3:
2:
4990:
4979:
4976:
4974:
4971:
4969:
4966:
4964:
4963:Number theory
4961:
4960:
4958:
4943:
4939:
4935:
4934:
4931:
4921:
4918:
4917:
4914:
4909:
4904:
4900:
4890:
4887:
4885:
4882:
4881:
4878:
4873:
4868:
4864:
4854:
4851:
4849:
4846:
4845:
4842:
4837:
4832:
4828:
4818:
4815:
4813:
4810:
4809:
4806:
4802:
4796:
4792:
4782:
4779:
4777:
4774:
4772:
4769:
4768:
4765:
4761:
4756:
4752:
4738:
4735:
4734:
4732:
4728:
4722:
4719:
4717:
4714:
4712:
4711:Polydivisible
4709:
4707:
4704:
4702:
4699:
4697:
4694:
4692:
4689:
4688:
4686:
4682:
4676:
4673:
4671:
4668:
4666:
4663:
4661:
4658:
4656:
4653:
4652:
4650:
4647:
4642:
4636:
4633:
4631:
4628:
4626:
4623:
4621:
4618:
4616:
4613:
4611:
4608:
4606:
4603:
4602:
4600:
4597:
4593:
4585:
4582:
4581:
4580:
4577:
4576:
4574:
4571:
4567:
4555:
4552:
4551:
4550:
4547:
4545:
4542:
4540:
4537:
4535:
4532:
4530:
4527:
4525:
4522:
4520:
4517:
4515:
4512:
4510:
4507:
4506:
4504:
4500:
4494:
4491:
4490:
4488:
4484:
4478:
4475:
4473:
4470:
4469:
4467:
4465:Digit product
4463:
4457:
4454:
4452:
4449:
4447:
4444:
4442:
4439:
4438:
4436:
4434:
4430:
4422:
4419:
4417:
4414:
4413:
4412:
4409:
4408:
4406:
4404:
4399:
4395:
4391:
4386:
4381:
4377:
4367:
4364:
4362:
4359:
4357:
4354:
4352:
4349:
4347:
4344:
4342:
4339:
4337:
4334:
4332:
4329:
4327:
4324:
4322:
4319:
4317:
4314:
4312:
4309:
4307:
4304:
4302:
4301:Erdős–Nicolas
4299:
4297:
4294:
4292:
4289:
4288:
4285:
4280:
4276:
4270:
4266:
4252:
4249:
4247:
4244:
4243:
4241:
4239:
4235:
4229:
4226:
4224:
4221:
4219:
4216:
4214:
4211:
4210:
4208:
4206:
4202:
4196:
4193:
4191:
4188:
4186:
4183:
4181:
4178:
4176:
4173:
4171:
4168:
4167:
4165:
4163:
4159:
4153:
4150:
4148:
4145:
4144:
4142:
4140:
4136:
4130:
4127:
4125:
4122:
4120:
4119:Superabundant
4117:
4115:
4112:
4110:
4107:
4105:
4102:
4100:
4097:
4095:
4092:
4090:
4087:
4085:
4082:
4080:
4077:
4075:
4072:
4070:
4067:
4065:
4062:
4060:
4057:
4055:
4052:
4050:
4047:
4045:
4042:
4040:
4037:
4035:
4032:
4030:
4027:
4025:
4022:
4021:
4019:
4017:
4013:
4009:
4005:
4001:
3996:
3992:
3982:
3979:
3977:
3974:
3972:
3969:
3967:
3964:
3962:
3959:
3957:
3954:
3952:
3949:
3947:
3944:
3942:
3939:
3937:
3934:
3932:
3929:
3927:
3924:
3923:
3920:
3916:
3911:
3907:
3897:
3894:
3892:
3889:
3887:
3884:
3882:
3879:
3878:
3875:
3871:
3866:
3862:
3852:
3849:
3847:
3844:
3842:
3839:
3837:
3834:
3832:
3829:
3827:
3824:
3822:
3819:
3817:
3814:
3812:
3809:
3807:
3804:
3802:
3799:
3797:
3794:
3792:
3789:
3787:
3784:
3782:
3779:
3777:
3774:
3772:
3769:
3767:
3764:
3762:
3759:
3757:
3754:
3753:
3750:
3743:
3739:
3721:
3718:
3716:
3713:
3711:
3708:
3707:
3705:
3701:
3698:
3696:
3695:4-dimensional
3692:
3682:
3679:
3678:
3676:
3674:
3670:
3664:
3661:
3659:
3656:
3654:
3651:
3649:
3646:
3644:
3641:
3639:
3636:
3635:
3633:
3631:
3627:
3621:
3618:
3616:
3613:
3611:
3608:
3606:
3605:Centered cube
3603:
3601:
3598:
3597:
3595:
3593:
3589:
3586:
3584:
3583:3-dimensional
3580:
3570:
3567:
3565:
3562:
3560:
3557:
3555:
3552:
3550:
3547:
3545:
3542:
3540:
3537:
3535:
3532:
3530:
3527:
3525:
3522:
3521:
3519:
3517:
3513:
3507:
3504:
3502:
3499:
3497:
3494:
3492:
3489:
3487:
3484:
3482:
3479:
3477:
3474:
3472:
3469:
3467:
3464:
3463:
3461:
3459:
3455:
3452:
3450:
3449:2-dimensional
3446:
3442:
3438:
3433:
3429:
3419:
3416:
3414:
3411:
3409:
3406:
3404:
3401:
3399:
3396:
3394:
3393:Nonhypotenuse
3391:
3390:
3387:
3380:
3376:
3366:
3363:
3361:
3358:
3356:
3353:
3351:
3348:
3346:
3343:
3342:
3339:
3332:
3328:
3318:
3315:
3313:
3310:
3308:
3305:
3303:
3300:
3298:
3295:
3293:
3290:
3288:
3285:
3283:
3280:
3279:
3276:
3271:
3266:
3262:
3252:
3249:
3247:
3244:
3242:
3239:
3237:
3234:
3232:
3229:
3228:
3225:
3218:
3214:
3204:
3201:
3199:
3196:
3194:
3191:
3189:
3186:
3184:
3181:
3179:
3176:
3174:
3171:
3170:
3167:
3162:
3156:
3152:
3142:
3139:
3137:
3134:
3132:
3131:Perfect power
3129:
3127:
3124:
3122:
3121:Seventh power
3119:
3117:
3114:
3112:
3109:
3107:
3104:
3102:
3099:
3097:
3094:
3092:
3089:
3087:
3084:
3082:
3079:
3077:
3074:
3073:
3070:
3065:
3060:
3056:
3052:
3044:
3039:
3037:
3032:
3030:
3025:
3024:
3021:
3005:
3002:
3000:
2997:
2995:
2992:
2990:
2987:
2986:
2984:
2980:
2977:
2975:
2970:
2960:
2957:
2955:
2952:
2950:
2947:
2946:
2944:
2940:
2937:
2935:
2934:4-dimensional
2931:
2921:
2918:
2916:
2913:
2912:
2910:
2908:
2904:
2898:
2895:
2893:
2890:
2888:
2885:
2883:
2880:
2878:
2875:
2874:
2872:
2870:
2866:
2860:
2857:
2855:
2852:
2850:
2847:
2845:
2842:
2840:
2837:
2836:
2834:
2832:
2828:
2825:
2823:
2822:3-dimensional
2819:
2809:
2806:
2804:
2801:
2799:
2796:
2794:
2791:
2789:
2786:
2784:
2781:
2779:
2776:
2774:
2771:
2769:
2766:
2765:
2763:
2761:
2757:
2751:
2748:
2746:
2743:
2741:
2738:
2736:
2733:
2731:
2728:
2726:
2723:
2721:
2718:
2716:
2713:
2711:
2708:
2707:
2705:
2703:
2699:
2696:
2694:
2693:2-dimensional
2690:
2686:
2679:
2674:
2672:
2667:
2665:
2660:
2659:
2656:
2650:
2646:
2643:
2640:
2636:
2635:
2630:
2626:
2621:
2620:
2616:
2608:
2603:
2599:
2595:
2591:
2587:
2586:
2581:
2577:
2573:
2569:
2565:
2560:
2559:10.37236/1854
2555:
2551:
2547:
2546:
2541:
2532:
2528:
2522:
2518:
2514:
2510:
2506:
2502:
2498:
2494:
2493:
2488:
2483:
2479:
2475:
2471:
2467:
2463:
2459:
2458:
2438:
2430:
2427:
2421:
2416:
2412:
2408:
2398:
2394:
2390:
2389:
2383:
2375:
2374:
2368:
2364:
2358:
2354:
2349:
2345:
2341:
2337:
2333:
2329:
2325:
2324:
2318:
2313:
2312:
2306:
2302:
2298:
2293:
2292:10.37236/1762
2288:
2284:
2280:
2279:
2274:
2265:
2262:
2258:
2254:
2250:
2246:
2242:
2238:
2234:
2230:
2226:
2225:
2220:
2216:
2208:
2207:
2202:
2198:
2194:
2190:
2186:
2182:
2178:
2174:
2173:
2165:
2161:
2157:
2153:
2149:
2145:
2141:
2137:
2133:
2129:
2128:
2120:
2103:
2091:
2087:
2084:
2081:
2068:
2063:
2059:
2055:
2044:
2040:
2039:
2034:
2027:
2022:
2019:
2014:
2013:
2007:
2003:
1997:
1994:
1988:
1986:
1984:
1980:
1976:
1972:
1970:
1966:
1958:
1956:
1954:
1953:Nelsen (1993)
1950:
1946:
1942:
1938:
1934:
1930:
1926:
1917:
1913:
1911:
1899:
1895:
1891:
1874:
1869:
1864:
1860:
1855:
1850:
1847:
1844:
1840:
1835:
1830:
1828:
1818:
1810:
1807:
1804:
1801:
1798:
1795:
1792:
1786:
1784:
1772:
1767:
1762:
1758:
1755:
1750:
1746:
1739:
1731:
1726:
1722:
1719:
1716:
1713:
1708:
1704:
1699:
1695:
1692:
1689:
1682:
1678:
1671:
1667:
1664:
1657:
1653:
1646:
1642:
1639:
1632:
1628:
1621:
1618:
1600:
1598:
1586:
1582:
1575:
1570:
1566:
1563:
1560:
1557:
1552:
1548:
1543:
1539:
1536:
1533:
1529:
1525:
1522:
1519:
1516:
1511:
1507:
1502:
1494:
1491:
1488:
1481:
1477:
1470:
1466:
1463:
1460:
1457:
1454:
1451:
1448:
1441:
1434:
1430:
1423:
1419:
1416:
1413:
1410:
1407:
1400:
1393:
1389:
1382:
1378:
1375:
1372:
1365:
1358:
1354:
1347:
1344:
1338:
1336:
1326:
1322:
1318:
1315:
1312:
1309:
1306:
1303:
1300:
1297:
1294:
1291:
1288:
1286:
1279:
1275:
1269:
1264:
1261:
1258:
1254:
1229:
1223:
1220:
1217:
1214:
1206:
1201:
1198:
1195:
1191:
1187:
1182:
1178:
1167:
1156:
1139:
1133:
1130:
1127:
1124:
1114:
1110:
1104:
1101:
1096:
1093:
1090:
1086:
1082:
1079:
1075:
1071:
1066:
1062:
1051:
1047:
1043:
1027:
1017:
1011:
1006:
1002:
999:
996:
993:
988:
984:
979:
975:
972:
969:
965:
961:
958:
955:
952:
949:
946:
941:
937:
932:
928:
924:
920:
917:
914:
911:
908:
905:
900:
896:
891:
887:
883:
879:
876:
873:
870:
865:
861:
856:
848:
843:
839:
830:
826:
819:
817:
814:
808:
803:
799:
792:
788:
783:and of pairs
781:
777:
770:
766:
755:
751:
747:
743:
733:
729:
725:
721:
694:
690:
656:
652:
648:
644:
638:
632:
628:
624:
619:
614:
612:
608:
604:
592:
588:
584:
580:
576:
571:
562:
549:= (1 + 2 + 3)
545:
538:
536:
527:
516:
512:
508:
504:
494:
490:
486:
482:
478:
474:
470:
465:
448:
444:
420:
416:
395:
391:
380:
376:
359:
355:
342:
334:
332:
329: 120 CE
316:
312:
308:
289:
284:
279:
275:
270:
265:
262:
259:
255:
250:
245:
240:
236:
230:
225:
222:
219:
215:
207:
206:
205:
203:
184:
179:
174:
170:
167:
164:
161:
158:
155:
152:
149:
146:
142:
137:
132:
128:
124:
121:
118:
113:
109:
105:
100:
96:
92:
87:
83:
75:
74:
73:
71:
63:
59:
52:
51:number theory
44:
43:Gulley (2010)
39:
33:
19:
4675:Transposable
4539:Narcissistic
4446:Digital root
4366:Super-Poulet
4326:Jordan–Pólya
4275:prime factor
4180:Noncototient
4147:Almost prime
4129:Superperfect
4104:Refactorable
4099:Quasiperfect
4074:Hyperperfect
3915:Pseudoprimes
3886:Wall–Sun–Sun
3821:Ordered Bell
3791:Fuss–Catalan
3714:
3703:non-centered
3653:Dodecahedral
3630:non-centered
3516:non-centered
3418:Wolstenholme
3163:× 2 ± 1
3160:
3159:Of the form
3126:Eighth power
3106:Fourth power
2982:non-centered
2953:
2942:non-centered
2877:Cube numbers
2869:non-centered
2760:non-centered
2750:Star numbers
2632:
2589:
2583:
2549:
2543:
2516:
2496:
2490:
2461:
2455:
2387:
2372:
2352:
2327:
2321:
2310:
2282:
2276:
2228:
2222:
2212:, AP Central
2205:
2176:
2170:
2131:
2125:
2021:
2009:
1996:
1973:
1962:
1945:Kanim (2004)
1933:Stein (1971)
1922:
1892:
1165:
1154:
1049:
1045:
823:
812:
801:
797:
790:
786:
779:
775:
768:
764:
753:
749:
745:
741:
731:
727:
723:
719:
692:
688:
654:
650:
646:
642:
639:
626:
622:
618:Stein (1971)
615:
600:
569:
466:
446:
442:
418:
414:
393:
389:
378:
374:
357:
353:
340:
338:
310:
304:
199:
48:
4696:Extravagant
4691:Equidigital
4646:permutation
4605:Palindromic
4579:Automorphic
4477:Sum-product
4456:Sum-product
4411:Persistence
4306:Erdős–Woods
4228:Untouchable
4109:Semiperfect
4059:Hemiperfect
3720:Tesseractic
3658:Icosahedral
3638:Tetrahedral
3569:Dodecagonal
3270:Recursively
3141:Prime power
3116:Sixth power
3111:Fifth power
3091:Power of 10
3049:Classes of
2974:dimensional
2592:: 145–151,
686:. That is,
559:= 1 + 2 + 3
533: 1500
522: 1300
499: 1000
72:. That is,
4957:Categories
4908:Graphemics
4781:Pernicious
4635:Undulating
4610:Pandigital
4584:Trimorphic
4185:Nontotient
4034:Arithmetic
3648:Octahedral
3549:Heptagonal
3539:Pentagonal
3524:Triangular
3365:Sierpiński
3287:Jacobsthal
3086:Power of 3
3081:Power of 2
2035:References
1965:power sums
1904:th row is
1894:Row (1893)
757:for which
712:that make
515:Gersonides
477:Nicomachus
4665:Parasitic
4514:Factorion
4441:Digit sum
4433:Digit sum
4251:Fortunate
4238:Primorial
4152:Semiprime
4089:Practical
4054:Descartes
4049:Deficient
4039:Betrothed
3881:Wieferich
3710:Pentatope
3673:pyramidal
3564:Decagonal
3559:Nonagonal
3554:Octagonal
3544:Hexagonal
3403:Practical
3350:Congruent
3282:Fibonacci
3246:Loeschian
2907:pyramidal
2634:MathWorld
2428:∑
2409:∑
2393:pp. 47–48
2261:126165678
2056:∑
1841:∑
1805:⋯
1732:⏟
1720:−
1693:⋯
1672:⏟
1647:⏟
1622:⏟
1576:⏟
1564:−
1537:⋯
1517:−
1492:⋯
1471:⏟
1424:⏟
1383:⏟
1348:⏟
1316:⋯
1255:∑
1221:−
1192:∑
1131:−
1094:−
1076:∑
1012:⏟
1000:−
973:⋯
947:−
906:−
871:−
718:1 ≤
678:and that
561:) squares
553:1 + 2 + 3
511:Al-Qabisi
493:Al-Karaji
485:Aryabhata
322: 60
256:∑
216:∑
202:summation
165:⋯
122:⋯
4737:Friedman
4670:Primeval
4615:Repdigit
4572:-related
4519:Kaprekar
4493:Meertens
4416:Additive
4403:dynamics
4311:Friendly
4223:Sociable
4213:Amicable
4024:Abundant
4004:dynamics
3826:Schröder
3816:Narayana
3786:Eulerian
3776:Delannoy
3771:Dedekind
3592:centered
3458:centered
3345:Amenable
3302:Narayana
3292:Leonardo
3188:Mersenne
3136:Powerful
3076:Achilles
2831:centered
2702:centered
2645:Archived
2578:(1854),
2536:"On the
2515:(1963),
2203:(2004),
2193:27646391
810:by
547:All 36 (
381:+ 1) − 1
313:, after
307:identity
4910:related
4874:related
4838:related
4836:Sorting
4721:Vampire
4706:Harshad
4648:related
4620:Repunit
4534:Lychrel
4509:Dudeney
4361:Størmer
4356:Sphenic
4341:Regular
4279:divisor
4218:Perfect
4114:Sublime
4084:Perfect
3811:Motzkin
3766:Catalan
3307:Padovan
3241:Leyland
3236:Idoneal
3231:Hilbert
3203:Woodall
2972:Higher
2594:Bibcode
2568:2114194
2505:1355130
2478:2688231
2344:3219288
2301:2034423
2273:-cubes"
2253:0096615
2245:3609189
2148:1559017
2004:(ed.),
1910:gnomons
827: (
458:
439:
430:
411:
405:
386:
369:
350:
335:History
64:of the
60:is the
4776:Odious
4701:Frugal
4655:Cyclic
4644:Digit-
4351:Smooth
4336:Pronic
4296:Cyclic
4273:Other
4246:Euclid
3896:Wilson
3870:Primes
3529:Square
3398:Polite
3360:Riesel
3355:Knödel
3317:Perrin
3198:Thabit
3183:Fermat
3173:Cullen
3096:Square
3064:Powers
2566:
2523:
2503:
2476:
2359:
2342:
2299:
2259:
2251:
2243:
2191:
2146:
1162:up to
820:Proofs
708:, and
593:, 225,
503:Persia
481:Jordan
62:square
4817:Prime
4812:Lucky
4801:sieve
4730:Other
4716:Smith
4596:Digit
4554:Happy
4529:Keith
4502:Other
4346:Rough
4316:Giuga
3781:Euler
3643:Cubic
3297:Lucas
3193:Proth
2474:JSTOR
2377:(PDF)
2340:JSTOR
2257:S2CID
2241:JSTOR
2210:(PDF)
2189:JSTOR
2167:(PDF)
2144:JSTOR
2122:(PDF)
1989:Notes
795:with
773:with
635:4 × 4
598:... .
489:India
305:This
58:cubes
4771:Evil
4451:Self
4401:and
4291:Blum
4002:and
3806:Lobb
3761:Cake
3756:Bell
3506:Star
3413:Ulam
3312:Pell
3101:Cube
2521:ISBN
2357:ISBN
2010:The
1981:and
1168:− 1)
829:1854
662:and
631:grid
609:and
557:14 (
449:+ 1)
421:+ 1)
396:+ 1)
360:+ 1)
4889:Ban
4277:or
3796:Lah
2602:doi
2554:doi
2466:doi
2454:",
2332:doi
2287:doi
2233:doi
2181:doi
2136:doi
616:As
591:100
501:in
487:in
331:).
68:th
49:In
4959::
2631:,
2627:,
2600:,
2588:,
2582:,
2564:MR
2562:,
2550:11
2548:,
2542:,
2501:MR
2497:97
2495:,
2489:,
2472:,
2462:44
2460:,
2338:,
2328:77
2326:,
2297:MR
2295:,
2283:11
2281:,
2275:,
2255:,
2249:MR
2247:,
2239:,
2229:41
2227:,
2187:,
2177:37
2175:,
2169:,
2158:;
2142:,
2132:33
2130:,
2124:,
2008:,
1931:.
1467:19
1461:17
1455:15
1449:13
1420:11
1310:64
1304:27
816:.
800:≤
789:,
778:≤
767:,
752:,
748:,
744:,
730:≤
726:,
722:,
704:,
691:=
653:,
649:,
645:,
625:×
613:.
589:,
587:36
585:,
581:,
577:,
551:=
530:c.
519:c.
505:.
496:c.
464:.
326:c.
324:–
319:c.
204::
3161:a
3042:e
3035:t
3028:v
2677:e
2670:t
2663:v
2611:.
2604::
2596::
2590:7
2571:.
2556::
2538:q
2530:.
2508:.
2481:.
2468::
2439:2
2435:)
2431:k
2425:(
2422:=
2417:3
2413:k
2396:.
2381:.
2366:.
2347:.
2334::
2316:.
2304:.
2289::
2271:q
2235::
2214:.
2196:.
2183::
2151:.
2138::
2119:"
2104:2
2097:)
2092:2
2088:1
2085:+
2082:n
2076:(
2069:=
2064:3
2060:k
2028:.
1906:i
1902:i
1875:.
1870:2
1865:)
1861:k
1856:n
1851:1
1848:=
1845:k
1836:(
1831:=
1819:2
1815:)
1811:n
1808:+
1802:+
1799:2
1796:+
1793:1
1790:(
1787:=
1773:2
1768:)
1763:2
1759:n
1756:+
1751:2
1747:n
1740:(
1727:)
1723:1
1717:n
1714:+
1709:2
1705:n
1700:(
1696:+
1690:+
1683:2
1679:3
1668:5
1665:+
1658:2
1654:2
1643:3
1640:+
1633:2
1629:1
1619:1
1601:=
1587:3
1583:n
1571:)
1567:1
1561:n
1558:+
1553:2
1549:n
1544:(
1540:+
1534:+
1530:)
1526:1
1523:+
1520:n
1512:2
1508:n
1503:(
1495:+
1489:+
1482:3
1478:4
1464:+
1458:+
1452:+
1442:+
1435:3
1431:3
1417:+
1414:9
1411:+
1408:7
1401:+
1394:3
1390:2
1379:5
1376:+
1373:3
1366:+
1359:3
1355:1
1345:1
1339:=
1327:3
1323:n
1319:+
1313:+
1307:+
1301:+
1298:8
1295:+
1292:1
1289:=
1280:3
1276:k
1270:n
1265:1
1262:=
1259:k
1230:,
1227:)
1224:1
1218:k
1215:2
1212:(
1207:n
1202:1
1199:=
1196:k
1188:=
1183:2
1179:n
1166:n
1164:(
1160:1
1155:n
1140:,
1137:)
1134:1
1128:k
1125:2
1122:(
1115:n
1111:T
1105:1
1102:+
1097:1
1091:n
1087:T
1083:=
1080:k
1072:=
1067:3
1063:n
1050:n
1046:T
1028:.
1018:n
1007:)
1003:1
997:n
994:+
989:2
985:n
980:(
976:+
970:+
966:)
962:4
959:+
956:1
953:+
950:n
942:2
938:n
933:(
929:+
925:)
921:2
918:+
915:1
912:+
909:n
901:2
897:n
892:(
888:+
884:)
880:1
877:+
874:n
866:2
862:n
857:(
849:=
844:3
840:n
813:n
802:W
798:Z
793:)
791:W
787:Z
785:(
780:Y
776:X
771:)
769:Y
765:X
763:(
759:W
754:W
750:Z
746:Y
742:X
737:W
732:n
728:Z
724:Y
720:X
714:W
710:Z
706:Y
702:X
698:W
693:P
689:P
684:Z
680:W
676:X
672:Y
668:W
664:n
660:1
655:W
651:Z
647:Y
643:X
627:n
623:n
583:9
579:1
575:0
528:(
517:(
461:)
455:2
452:/
447:n
445:(
443:n
436:(
427:2
424:/
419:n
417:(
415:n
402:2
399:/
394:n
392:(
390:n
379:n
377:(
375:n
366:2
363:/
358:n
356:(
354:n
345:n
317:(
290:.
285:2
280:)
276:k
271:n
266:1
263:=
260:k
251:(
246:=
241:3
237:k
231:n
226:1
223:=
220:k
185:.
180:2
175:)
171:n
168:+
162:+
159:3
156:+
153:2
150:+
147:1
143:(
138:=
133:3
129:n
125:+
119:+
114:3
110:3
106:+
101:3
97:2
93:+
88:3
84:1
66:n
55:n
34:.
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.