190:. This issue can be avoided by "regularizing" the problem so as to exclude diameters, without affecting the resulting probabilities. But as presented above, in method 1, each chord can be chosen in exactly one way, regardless of whether or not it is a diameter; in method 2, each diameter can be chosen in two ways, whereas each other chord can be chosen in only one way; and in method 3, each choice of midpoint corresponds to a single chord, except the center of the circle, which is the midpoint of all the diameters.
305:
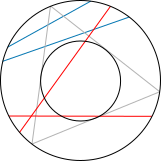
the chords on that smaller circle needs to be the same as the restricted distribution of chords on the larger circle (again using extension/restriction of the generating straws). Thus, if the smaller circle is moved around within the larger circle, the restricted distribution should not change. It can be seen very easily that there would be a change for method 3: the chord distribution on the small red circle looks qualitatively different from the distribution on the large circle:
352:"Method 2" is the only solution that fulfills the transformation invariants that are present in certain physical systems—such as in statistical mechanics and gas physics—in the specific case of Jaynes's proposed experiment of throwing straws from a distance onto a small circle. Nevertheless, one can design other practical experiments that give answers according to the other methods. For example, in order to arrive at the solution of "method 1", the
309:
225:
215:
205:
257:
247:
237:
143:
107:
79:
343:
Likewise, "method 1" is the unique invariant distribution for a scenario where a spinner is used to select one endpoint of the chord, and then used again to select the orientation of the chord. Here the invariance in question consists of rotational invariance for each of the two spins. It is also the
304:
To illustrate: assume that chords are laid at random onto a circle with a diameter of 2, say by throwing straws onto it from far away and converting them to chords by extension/restriction. Now another circle with a smaller diameter (e.g., 1.1) is laid into the larger circle. Then the distribution of
85:
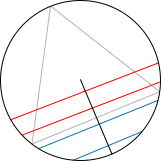
The "random endpoints" method: Choose two random points on the circumference of the circle and draw the chord joining them. To calculate the probability in question imagine the triangle rotated so its vertex coincides with one of the chord endpoints. Observe that if the other chord endpoint lies on
289:
proposed a solution to
Bertrand's paradox based on the principle of "maximum ignorance"—that we should not use any information that is not given in the statement of the problem. Jaynes pointed out that Bertrand's problem does not specify the position or size of the circle and argued that therefore
121:
to the radius. The chord is longer than a side of the triangle if the chosen point is nearer the center of the circle than the point where the side of the triangle intersects the radius. The side of the triangle bisects the radius, therefore the probability a random chord is longer than a side of
356:
method, one can affix a spinner to the center of the circle, and let the results of two independent spins mark the endpoints of the chord. In order to arrive at the solution of "method 3", one could cover the circle with molasses and mark the first point that a fly lands on as the midpoint of the
331:
In a 2015 article, Alon Drory argued that Jaynes' principle can also yield
Bertrand's other two solutions. Drory argues that the mathematical implementation of the above invariance properties is not unique, but depends on the underlying procedure of random selection that one uses (as mentioned
86:
the arc between the endpoints of the triangle side opposite the first point, the chord is longer than a side of the triangle. The length of the arc is one third of the circumference of the circle, therefore the probability that a random chord is longer than a side of the inscribed triangle is
319:
However, Jaynes did not just use invariances to accept or reject given methods: this would leave the possibility that there is another not yet described method that would meet his common-sense criteria. Jaynes used the integral equations describing the invariances to directly determine the
276:
The problem's classical solution (presented, for example, in
Bertrand's own work) depends on the method by which a chord is chosen "at random". The argument is that if the method of random selection is specified, the problem will have a well-defined solution (determined by the principle of
332:
above, Jaynes used a straw-throwing method to choose random chords). He shows that each of
Bertrand's three solutions can be derived using rotational, scaling, and translational invariance, concluding that Jaynes' principle is just as subject to interpretation as the
149:
The "random midpoint" method: Choose a point anywhere within the circle and construct a chord with the chosen point as its midpoint. The chord is longer than a side of the inscribed triangle if the chosen point falls within a concentric circle of radius
277:
indifference). The three solutions presented by
Bertrand correspond to different selection methods, and in the absence of further information there is no reason to prefer one over another; accordingly, the problem as stated has no unique solution.
344:
unique scale and rotation invariant distribution for a scenario where a rod is placed vertically over a point on the circle's circumference, and allowed to drop to the horizontal position (conditional on it landing partly inside the circle).
339:
For example, we may consider throwing a dart at the circle, and drawing the chord having the chosen point as its center. Then the unique distribution which is translation, rotation, and scale invariant is the one called "method 3" above.
315:
The same occurs for method 1, though it is harder to see in a graphical representation. Method 2 is the only one that is both scale invariant and translation invariant; method 3 is just scale invariant, method 1 is neither.
166:
the radius of the larger circle. The area of the smaller circle is one fourth the area of the larger circle, therefore the probability a random chord is longer than a side of the inscribed triangle is
776:
771:
20:
866:
761:
660:
113:
The "random radial point" method: Choose a radius of the circle, choose a point on the radius and construct the chord through this point and
357:
chord. Several observers have designed experiments in order to obtain the different solutions and verified the results empirically.
324:. In this problem, the integral equations indeed have a unique solution, and it is precisely what was called "method 2" above, the
39:
871:
548:
402:
73:
Bertrand gave three arguments (each using the principle of indifference), all apparently valid yet yielding different results:
290:
any definite and objective solution must be "indifferent" to size and position. In other words: the solution must be both
861:
648:
333:
70:
of the circle is chosen at random. What is the probability that the chord is longer than a side of the triangle?
47:
677:
321:
31:
793:
298:
594:
447:
295:
50:
may not produce definite, well-defined results for probabilities if it is applied uncritically when the
394:
603:
466:
117:
to the radius. To calculate the probability in question imagine the triangle rotated so a side is
724:
702:
694:
619:
565:
528:
482:
456:
419:
291:
35:
809:
757:
656:
652:
641:
520:
51:
785:
686:
611:
557:
512:
474:
411:
67:
268:
Other selection methods have been found. In fact, there exists an infinite family of them.
372:
376:
607:
470:
636:
308:
812:
445:
Drory, Alon (2015), "Failure and Uses of Jaynes' Principle of
Transformation Groups",
224:
214:
204:
855:
706:
569:
118:
114:
486:
423:
186:
These three selection methods differ as to the weight they give to chords which are
623:
582:
286:
82:
Random chords, selection method 1; red = longer than triangle side, blue = shorter
747:
846:
842:
62:
The
Bertrand paradox is generally presented as follows: Consider an equilateral
586:
256:
246:
236:
142:
106:
78:
835:
827:
478:
524:
817:
753:
63:
789:
643:
The Second
Scientific American Book of Mathematical Puzzles and Diversions
280:
719:
187:
698:
615:
532:
500:
690:
516:
561:
461:
415:
307:
255:
245:
235:
223:
213:
203:
141:
105:
77:
546:
Marinoff, L. (1994), "A resolution of
Bertrand's paradox",
196:
midpoints/chords chosen at random using the above methods.
501:"Note Concerning Two Problems in Geometrical Probability"
281:
Jaynes's solution using the "maximum ignorance" principle
228:
Midpoints of the chords chosen at random using method 3
218:
Midpoints of the chords chosen at random using method 2
208:
Midpoints of the chords chosen at random using method 1
395:"Bertrand's Paradox and the Principle of Indifference"
194:
Scatterplots showing simulated
Bertrand distributions,
722:(May–June 1984), "Marginalia: more on randomness",
675:Tissler, P.E. (March 1984), "Bertrand's Paradox",
640:
777:British Journal for the Philosophy of Science
8:
770:Gyenis, Zalán; Rédei, Miklós (1 June 2015),
685:(443), The Mathematical Association: 15–19,
285:In his 1973 paper "The Well-Posed Problem",
19:For other paradoxes by Joseph Bertrand, see
57:
460:
440:
438:
436:
434:
432:
365:
46:(1889) as an example to show that the
58:Bertrand's formulation of the problem
7:
21:Bertrand's paradox (disambiguation)
14:
505:The American Mathematical Monthly
260:Chords chosen at random, method 3
250:Chords chosen at random, method 2
240:Chords chosen at random, method 1
146:Random chords, selection method 3
110:Random chords, selection method 2
64:triangle inscribed in a circle
1:
772:"Defusing Bertrand's Paradox"
867:Probability theory paradoxes
649:University of Chicago Press
888:
837:More on Bertrand's Paradox
122:the inscribed triangle is
42:introduced it in his work
18:
16:Probability theory paradox
479:10.1007/s10701-015-9876-7
334:principle of indifference
48:principle of indifference
678:The Mathematical Gazette
587:"The Well-Posed Problem"
322:probability distribution
32:classical interpretation
30:is a problem within the
746:Clark, Michael (2012),
377:Calcul des probabilités
52:domain of possibilities
44:Calcul des probabilités
872:Mathematical paradoxes
595:Foundations of Physics
448:Foundations of Physics
312:
261:
251:
241:
229:
219:
209:
147:
111:
83:
749:Paradoxes from A to Z
549:Philosophy of Science
499:Bower, O. K. (1934).
403:Philosophy of Science
311:
259:
249:
239:
227:
217:
207:
145:
109:
81:
813:"Bertrand's Problem"
393:Shackel, N. (2007),
348:Physical experiments
862:Eponymous paradoxes
790:10.1093/bjps/axt036
608:1973FoPh....3..477J
471:2015FoPh...45..439D
829:Bertrand's Paradox
810:Weisstein, Eric W.
725:American Scientist
616:10.1007/BF00709116
313:
272:Classical solution
262:
252:
242:
230:
220:
210:
148:
112:
84:
36:probability theory
763:978-0-415-53857-2
662:978-0-226-28253-4
266:
265:
879:
840:
832:
823:
822:
797:
796:on 5 August 2014
792:, archived from
766:
752:(3rd ed.),
734:
733:
716:
710:
709:
672:
666:
665:
646:
633:
627:
626:
591:
579:
573:
572:
543:
537:
536:
496:
490:
489:
464:
442:
427:
426:
399:
390:
384:
381:Gauthier-Villars
373:Bertrand, Joseph
370:
354:random endpoints
200:
199:
181:
179:
178:
175:
172:
165:
163:
162:
159:
156:
137:
135:
134:
131:
128:
101:
99:
98:
95:
92:
28:Bertrand paradox
887:
886:
882:
881:
880:
878:
877:
876:
852:
851:
834:
826:
808:
807:
804:
769:
764:
745:
742:
740:Further reading
737:
718:
717:
713:
691:10.2307/3615385
674:
673:
669:
663:
637:Gardner, Martin
635:
634:
630:
589:
581:
580:
576:
545:
544:
540:
517:10.2307/2300418
498:
497:
493:
444:
443:
430:
397:
392:
391:
387:
371:
367:
363:
350:
283:
274:
198:
195:
176:
173:
170:
169:
167:
160:
157:
154:
153:
151:
132:
129:
126:
125:
123:
96:
93:
90:
89:
87:
60:
40:Joseph Bertrand
24:
17:
12:
11:
5:
885:
883:
875:
874:
869:
864:
854:
853:
850:
849:
824:
803:
802:External links
800:
799:
798:
784:(2): 349–373,
767:
762:
741:
738:
736:
735:
711:
667:
661:
628:
602:(4): 477–493,
574:
562:10.1086/289777
538:
511:(8): 506–510.
491:
455:(4): 439–460,
428:
416:10.1086/519028
410:(2): 150–175,
385:
364:
362:
359:
349:
346:
282:
279:
273:
270:
264:
263:
253:
243:
232:
231:
221:
211:
192:
184:
183:
139:
103:
59:
56:
15:
13:
10:
9:
6:
4:
3:
2:
884:
873:
870:
868:
865:
863:
860:
859:
857:
848:
844:
839:
838:
831:
830:
825:
820:
819:
814:
811:
806:
805:
801:
795:
791:
787:
783:
779:
778:
773:
768:
765:
759:
755:
751:
750:
744:
743:
739:
731:
727:
726:
721:
715:
712:
708:
704:
700:
696:
692:
688:
684:
680:
679:
671:
668:
664:
658:
654:
650:
645:
644:
638:
632:
629:
625:
621:
617:
613:
609:
605:
601:
597:
596:
588:
584:
583:Jaynes, E. T.
578:
575:
571:
567:
563:
559:
555:
551:
550:
542:
539:
534:
530:
526:
522:
518:
514:
510:
506:
502:
495:
492:
488:
484:
480:
476:
472:
468:
463:
458:
454:
450:
449:
441:
439:
437:
435:
433:
429:
425:
421:
417:
413:
409:
405:
404:
396:
389:
386:
382:
378:
374:
369:
366:
360:
358:
355:
347:
345:
341:
337:
335:
329:
327:
326:random radius
323:
317:
310:
306:
302:
300:
297:
293:
288:
278:
271:
269:
258:
254:
248:
244:
238:
234:
233:
226:
222:
216:
212:
206:
202:
201:
197:
191:
189:
144:
140:
120:
119:perpendicular
116:
115:perpendicular
108:
104:
80:
76:
75:
74:
71:
69:
65:
55:
54:is infinite.
53:
49:
45:
41:
37:
33:
29:
22:
836:
828:
816:
794:the original
781:
775:
748:
732:(3): 282–283
729:
723:
714:
682:
676:
670:
642:
631:
599:
593:
577:
553:
547:
541:
508:
504:
494:
452:
446:
407:
401:
388:
380:
368:
353:
351:
342:
338:
330:
325:
318:
314:
303:
287:Edwin Jaynes
284:
275:
267:
193:
185:
72:
66:. Suppose a
61:
43:
27:
25:
847:3Blue1Brown
843:Numberphile
651:, pp.
296:translation
856:Categories
462:1503.09072
818:MathWorld
754:Routledge
720:Kac, Mark
707:158690181
570:122224925
525:0002-9890
383:, p. 5-6.
375:(1889), "
299:invariant
188:diameters
639:(1987),
585:(1973),
556:: 1–24,
487:88515906
424:15760612
336:itself.
328:method.
699:3615385
653:223–226
624:2380040
604:Bibcode
533:2300418
467:Bibcode
180:
168:
164:
152:
136:
124:
100:
88:
845:&
760:
705:
697:
659:
622:
568:
531:
523:
485:
422:
703:S2CID
695:JSTOR
620:S2CID
590:(PDF)
566:S2CID
529:JSTOR
483:S2CID
457:arXiv
420:S2CID
398:(PDF)
361:Notes
292:scale
68:chord
833:and
758:ISBN
657:ISBN
521:ISSN
294:and
26:The
841:by
786:doi
687:doi
612:doi
558:doi
513:doi
475:doi
412:doi
379:",
34:of
858::
815:.
782:66
780:,
774:,
756:,
730:72
728:,
701:,
693:,
683:68
681:,
655:,
647:,
618:,
610:,
598:,
592:,
564:,
554:61
552:,
527:.
519:.
509:41
507:.
503:.
481:,
473:,
465:,
453:45
451:,
431:^
418:,
408:74
406:,
400:,
301:.
182:.
38:.
821:.
788::
689::
614::
606::
600:3
560::
535:.
515::
477::
469::
459::
414::
177:4
174:/
171:1
161:2
158:/
155:1
138:.
133:2
130:/
127:1
102:.
97:3
94:/
91:1
23:.
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.