24:
299:
when (α, β) is on the line and higher when it is above and to the right. Therefore, the significant terms near the origin under this assumption are only those lying on the line and the others may be ignored; it produces a simple approximate equation for the curve. There may be several such
263:
Specifically, draw a diagonal line connecting two points on the diagram so that every other point is either on or to the right and above it. There is at least one such line if the curve passes through the origin. Let the equation of the line be
502:
is the degree of the curve, is added to form a triangle which contains the diagram. This method considers all lines which bound the smallest convex polygon which contains the plotted points (see
188:
If the curve passes through the origin then determine the tangent lines there. For algebraic curves, this can be done by removing all but the terms of lowest order from the equation and solving.
370:
300:
diagonal lines, each corresponding to one or more branches of the curve, and the approximate equations of the branches may be found by applying this method to each line in turn.
470:
423:
91:
given its equation, without computing the large numbers of points required for a detailed plot. It is an application of the theory of curves to find their main features.
376:
Then Newton's diagram has points at (3, 0), (1, 1), and (0, 3). Two diagonal lines may be drawn as described above, 2α+β=3 and α+2β=3. These produce
253:) is a technique for determining the shape of an algebraic curve close to and far away from the origin. It consists of plotting (α, β) for each term
515:
191:
Similarly, removing all but the terms of highest order from the equation and solving gives the points where the curve meets the
202:
of the curve. Also determine from which side the curve approaches the asymptotes and where the asymptotes intersect the curve.
668:
663:
483:
475:
as approximate equations for the horizontal and vertical branches of the curve where they cross at the origin.
230:
260:
in the equation of the curve. The resulting diagram is then analyzed to produce information about the curve.
17:
551:
313:
658:
536:
429:
382:
304:
167:
147:
99:
The following are usually easy to carry out and give important clues as to the shape of a curve:
60:
628:
210:
561:
218:
214:
206:
192:
68:
684:
546:
541:
494:). The points (α, β) are plotted as with Newton's diagram method but the line α+β=
566:
556:
519:
64:
678:
639:
250:
503:
88:
23:
48:
199:
221:
respectively. If the equation of the curve cannot be solved explicitly for
158:-axis is an axis of symmetry for the curve. If the sum of the degrees of
76:
531:
87:) are techniques for producing a rough idea of overall shape of a
22:
166:
in each term is always even or always odd, then the curve is
486:
extended Newton's diagram to form a technique called the
138:
Determine the symmetry of the curve. If the exponent of
131:
equal to 0 in the equation of the curve and solving for
119:
equal to 0 in the equation of the curve and solving for
627:
Hilton, Harold (1920). "Chapter III: Curve-Tracing".
432:
385:
316:
154:
is always even in the equation of the curve then the
142:
is always even in the equation of the curve then the
464:
417:
364:
150:for the curve. Similarly, if the exponent of
8:
461:
437:
431:
414:
390:
384:
361:
334:
321:
315:
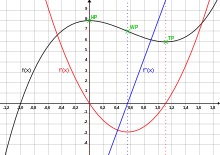
71:("WP"), of the black curve, respectively.
641:An Elementary Treatise on Curve Tracing
578:
276:. Suppose the curve is approximated by
597:
585:
177:Determine any bounds on the values of
609:
229:, finding these derivatives requires
59:value of the red, or the blue, curve
7:
365:{\displaystyle x^{3}+y^{3}-3axy=0\,}
14:
127:intercepts are found by setting
115:intercepts are found by setting
284:near the origin. Then the term
1:
465:{\displaystyle y^{2}-3ax=0\,}
418:{\displaystyle x^{2}-3ay=0\,}
111:intercepts of the curve. The
63:(becomes 0) gives rise to a
664:Encyclopedia of Mathematics
307:is defined by the equation
170:and the origin is called a
67:(marked "HP", "TP"), or an
35:+8 (black) and its first (9
701:
168:symmetric about the origin
15:
657:Trenogin, V.A. (2001) ,
638:Frost, Percival (1918).
231:implicit differentiation
16:Not to be confused with
479:The analytical triangle
237:
27:Graph of the function 3
18:Digital curve sketching
630:Plane Algebraic Curves
552:Numerical continuation
466:
419:
366:
247:Newton's parallelogram
72:
467:
420:
367:
43:, red) and second (18
26:
430:
383:
314:
146:-axis is an axis of
488:analytical triangle
305:folium of Descartes
462:
415:
362:
295:. The exponent is
211:second derivatives
73:
600:, Chapter III §3)
588:, Chapter III §2)
492:de Gua's triangle
303:For example, the
291:is approximately
219:inflection points
215:stationary points
213:to 0 to find the
123:. Similarly, the
692:
671:
659:"Newton diagram"
645:
634:
613:
607:
601:
595:
589:
583:
562:Boundary tracing
471:
469:
468:
463:
442:
441:
424:
422:
421:
416:
395:
394:
371:
369:
368:
363:
339:
338:
326:
325:
243:Newton's diagram
238:Newton's diagram
193:line at infinity
95:Basic techniques
69:inflection point
55:value where the
700:
699:
695:
694:
693:
691:
690:
689:
675:
674:
656:
653:
648:
637:
626:
622:
617:
616:
608:
604:
596:
592:
584:
580:
575:
547:Parent function
542:Algebraic curve
528:
512:
481:
433:
428:
427:
386:
381:
380:
330:
317:
312:
311:
245:(also known as
240:
97:
81:curve sketching
21:
12:
11:
5:
698:
696:
688:
687:
677:
676:
673:
672:
652:
651:External links
649:
647:
646:
635:
623:
621:
618:
615:
614:
602:
590:
577:
576:
574:
571:
570:
569:
567:Triangle strip
564:
559:
557:Marching cubes
554:
549:
544:
539:
534:
527:
524:
523:
522:
520:fluid dynamics
511:
508:
480:
477:
473:
472:
460:
457:
454:
451:
448:
445:
440:
436:
425:
413:
410:
407:
404:
401:
398:
393:
389:
374:
373:
360:
357:
354:
351:
348:
345:
342:
337:
333:
329:
324:
320:
239:
236:
235:
234:
203:
198:Determine the
196:
189:
186:
175:
136:
103:Determine the
96:
93:
65:local extremum
13:
10:
9:
6:
4:
3:
2:
697:
686:
683:
682:
680:
670:
666:
665:
660:
655:
654:
650:
643:
642:
636:
632:
631:
625:
624:
619:
612:, Chapter IX)
611:
606:
603:
599:
594:
591:
587:
582:
579:
572:
568:
565:
563:
560:
558:
555:
553:
550:
548:
545:
543:
540:
538:
535:
533:
530:
529:
525:
521:
517:
514:
513:
509:
507:
505:
501:
497:
493:
489:
485:
478:
476:
458:
455:
452:
449:
446:
443:
438:
434:
426:
411:
408:
405:
402:
399:
396:
391:
387:
379:
378:
377:
358:
355:
352:
349:
346:
343:
340:
335:
331:
327:
322:
318:
310:
309:
308:
306:
301:
298:
294:
290:
287:
283:
279:
275:
271:
267:
261:
259:
256:
252:
248:
244:
232:
228:
224:
220:
216:
212:
208:
204:
201:
197:
194:
190:
187:
184:
180:
176:
174:of the curve.
173:
169:
165:
161:
157:
153:
149:
145:
141:
137:
134:
130:
126:
122:
118:
114:
110:
106:
102:
101:
100:
94:
92:
90:
86:
85:curve tracing
82:
78:
70:
66:
62:
58:
54:
50:
46:
42:
38:
34:
30:
25:
19:
662:
644:. MacMillan.
640:
629:
605:
598:Hilton (1920
593:
586:Hilton (1920
581:
510:Applications
499:
495:
491:
487:
482:
474:
375:
302:
296:
292:
288:
285:
281:
277:
273:
269:
265:
262:
257:
254:
251:Isaac Newton
246:
242:
241:
226:
222:
182:
178:
171:
163:
159:
155:
151:
143:
139:
132:
128:
124:
120:
116:
112:
108:
104:
98:
84:
80:
74:
56:
52:
44:
40:
36:
32:
28:
610:Frost (1918
518:tracing in
504:convex hull
89:plane curve
49:derivatives
47:-10, blue)
620:References
516:Streamline
200:asymptotes
669:EMS Press
633:. Oxford.
444:−
397:−
341:−
679:Category
526:See also
498:, where
249:, after
148:symmetry
77:geometry
61:vanishes
205:Equate
685:Curves
484:De Gua
172:center
537:Locus
532:Curve
207:first
51:. An
573:Note
490:(or
217:and
209:and
181:and
162:and
107:and
83:(or
506:).
297:r/q
225:or
75:In
39:-10
681::
667:,
661:,
293:Dx
286:Ax
282:Cx
272:β=
268:α+
255:Ax
79:,
31:-5
500:n
496:n
459:0
456:=
453:x
450:a
447:3
439:2
435:y
412:0
409:=
406:y
403:a
400:3
392:2
388:x
372:.
359:0
356:=
353:y
350:x
347:a
344:3
336:3
332:y
328:+
323:3
319:x
289:y
280:=
278:y
274:r
270:p
266:q
258:y
233:.
227:y
223:x
195:.
185:.
183:y
179:x
164:y
160:x
156:x
152:y
144:y
140:x
135:.
133:y
129:x
125:y
121:x
117:y
113:x
109:y
105:x
57:y
53:x
45:x
41:x
37:x
33:x
29:x
20:.
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.