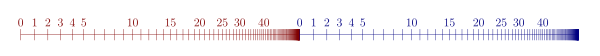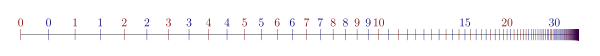846:
899:
6064:
4900:
showed that the ordinals satisfy a form of the unique factorization theorem: every nonzero ordinal can be written as a product of a finite number of prime ordinals. This factorization into prime ordinals is in general not unique, but there is a "minimal" factorization into primes that is unique up to
3982:
6416:
4175:
4769:
5958:
6234:
3228:
4301:
6491:
5913:
7735:. The ordinals do not have unique factorization into primes under the natural product. While the full polynomial ring does have unique factorization, the subset of polynomials with non-negative coefficients does not: for example, if
7697:. The natural product is associative and commutative and distributes over the natural sum. The natural product is always greater or equal to the usual product, but it may be strictly greater. For example, the natural product of
6306:
4536:
6775:
3637:
2496:
2309:
1160:
2107:
4889:, and so on. At the first occurrence of inequality, the ordinal that has the larger component is the larger ordinal. If they are the same until one terminates before the other, then the one that terminates first is smaller.
5806:
4637:
643:
587:
5584:
315:
5518:
3706:
3356:
7082:
7216:
7139:
5329:. We can do away with the infinitely many numerals by using just the constant symbol 0 and the operation of successor, S (for example, the natural number 4 may be expressed as S(S(S(S(0))))). This describes an
3865:
6622:
6712:
6311:
6558:
6110:
4066:
6956:
5676:
6851:
6816:
5630:
6996:
7036:
5728:
6156:
5979:
4074:
6884:
6917:
4413:
757:
4648:
3543:
3291:
7242:
5837:
4444:
4335:
3477:
7165:
3799:
5832:
5325:
can be expressed in an alphabet containing only the function symbols for addition, multiplication and exponentiation, as well as constant symbols for each natural number and for
4366:
6584:
3510:
2659:
with finite support, typically a set of much smaller cardinality. To avoid confusing ordinal exponentiation with cardinal exponentiation, one can use symbols for ordinals (e.g.
6648:
6520:
4567:
7458:
2159:
can be viewed as triples of natural numbers, ordered lexicographically with least significant position first. This agrees with the ordinary exponentiation of natural numbers.
7414:
6161:
1474:
Multiplication of ordinals is not in general commutative. Specifically, a natural number greater than 1 never commutes with any infinite ordinal, and two infinite ordinals
6674:
3123:
2688:
4860:
4806:
3853:
3826:
3424:
6496:
The natural sum and product are commutative and associative, and natural product distributes over natural sum. The operations are also monotonic, in the sense that if
5933:
3766:
3444:
783:
6421:
5953:
4887:
4833:
4206:
The Cantor normal form also allows us to compute sums and products of ordinals: to compute the sum, for example, one need merely know (see the properties listed in
7370:
7341:
7682:
The natural sum is associative and commutative. It is always greater or equal to the usual sum, but it may be strictly greater. For example, the natural sum of
7304:
7284:
6059:{\displaystyle \alpha \otimes \beta =\bigoplus _{\begin{aligned}&1\leq i\leq k\\&1\leq j\leq \ell \end{aligned}}\omega ^{\alpha _{i}\oplus \beta _{j}}.}
6239:
4449:
6720:
3562:
2391:
2204:
1105:
2044:
5351:, but because there are only countably many finite-length strings over any finite alphabet, for any given ordinal notation there will be ordinals below
5733:
4908:
A prime ordinal is an ordinal greater than 1 that cannot be written as a product of two smaller ordinals. Some of the first primes are 2, 3, 5, ... ,
598:
542:
5523:
4220:
260:
5457:
5054:
If two consecutive primes of the prime factorization are both limits or both finite, the second one must be less than or equal to the first one.
3646:
361:
is obtained by two copies of the natural numbers ordered in the usual fashion and the second copy completely to the right of the first. Writing
7966:
4575:
3296:
3092:
There are ordinal operations that continue the sequence begun by addition, multiplication, and exponentiation, including ordinal versions of
5372:
7041:
3977:{\displaystyle \omega ^{\omega ^{\omega ^{7}\cdot 6+\omega +42}\cdot 1729+\omega ^{9}+88}\cdot 3+\omega ^{\omega ^{\omega }}\cdot 5+65537}
3748:
that are built from the natural numbers by a finite number of arithmetical operations of addition, multiplication and exponentiation base-
7170:
7090:
66:. Cantor normal form provides a standardized way of writing ordinals. In addition to these usual ordinal operations, there are also the
7792:
has two incompatible expressions as a natural product of polynomials with non-negative coefficients that cannot be decomposed further.
6411:{\displaystyle \alpha \otimes \beta =\omega ^{\omega ^{\omega }+\omega }+\omega ^{\omega ^{\omega }+5}+\omega ^{\omega +1}+\omega ^{6}}
7679:
for the definition of natural multiplication in that context; however, it uses surreal subtraction, which is not defined on ordinals.
6589:
6679:
7987:
4992:
4971:
1763:
828:
7882:
6525:
6069:
4024:
533:
7847:
6922:
5635:
5335:: a system for naming ordinals over a finite alphabet. This particular system of ordinal notation is called the collection of
4002:
of the finite-length arithmetical expressions of Cantor normal form that are hereditarily non-trivial where non-trivial means
6821:
6783:
5589:
3545:. In that case Cantor normal form does not express the ordinal in terms of smaller ones; this can happen as explained below.
6961:
7001:
5681:
6115:
3995:
3074:
1755:, since they are not even a ring; furthermore the Euclidean "norm" would be ordinal-valued using the left division here.
7998:
7898:
4170:{\displaystyle 0,\,1=\omega ^{0},\,\omega =\omega ^{1},\,\omega ^{\omega },\,\omega ^{\omega ^{\omega }},\,\ldots \,.}
1303:
As is the case with addition, ordinal multiplication on the natural numbers is the same as standard multiplication.
6856:
4764:{\displaystyle \alpha n=\omega ^{\beta _{1}}c_{1}n+\omega ^{\beta _{2}}c_{2}+\cdots +\omega ^{\beta _{k}}c_{k}\,,}
4068:, i.e. in Cantor normal form the exponent is not smaller than the ordinal itself. It is the limit of the sequence
3559:
equal to 1 and allow the exponents to be equal. In other words, every ordinal number α can be uniquely written as
3548:
A minor variation of Cantor normal form, which is usually slightly easier to work with, is to set all the numbers
6889:
5361:
3396:
1508:" is an equivalence relation on the ordinals greater than 1, and all equivalence classes are countably infinite.
718:
7956:
8042:
4185:
3515:
3237:
4446:
the expression is already in Cantor normal form); and to compute products, the essential facts are that when
2179:
expresses the fact that finite sequences of zeros and ones can be identified with natural numbers, using the
7994:
7806:
There are arithmetic operations on ordinals by virtue of the one-to-one correspondence between ordinals and
7716:
7221:
5365:
4371:
3449:
2620:
7144:
3771:
7878:
5811:
979:. The order-type of the Cartesian product is the ordinal that results from multiplying the order-types of
7843:
7247:
The natural sum and product are the same as the addition and multiplication (restricted to ordinals) of
6563:
3482:
1859:
1322:
968:
141:
91:
63:
6627:
6499:
5047:. However, there is a unique factorization into primes satisfying the following additional conditions:
4418:
4309:
7725:. Under natural addition and multiplication, the ordinals can be identified with the elements of the
7419:
6229:{\displaystyle \alpha \oplus \beta =\omega ^{\omega ^{\omega }}+\omega ^{\omega }+\omega ^{5}+\omega }
8003:, Polska Akademia Nauk Monografie Matematyczne, vol. 34, Warsaw: Państwowe Wydawnictwo Naukowe,
7877:
Philip W. Carruth, Arithmetic of ordinals with applications to the theory of ordered
Abelian groups,
7866:
7375:
3223:{\displaystyle \omega ^{\beta _{1}}c_{1}+\omega ^{\beta _{2}}c_{2}+\cdots +\omega ^{\beta _{k}}c_{k}}
4340:
8037:
7263:
7252:
1863:
529:
6653:
5375:, and more general primitive recursive ordinal functions can be used to describe larger ordinals.
5153:. Repeating this and factorizing the natural numbers into primes gives the prime factorization of
4541:
7913:
5392:
2666:
2623:, the two operations are quite different and should not be confused. The cardinal exponentiation
7504:
is the maximum order type of a total order extending the direct product (as a partial order) of
7486:
is the maximum order type of a total order extending the disjoint union (as a partial order) of
4838:
4784:
3831:
3804:
3402:
6486:{\displaystyle \alpha \beta =\omega ^{\omega ^{\omega }+\omega }+\omega ^{\omega ^{\omega }+5}}
5908:{\displaystyle \alpha \oplus \beta =\omega ^{\gamma _{1}}+\cdots +\omega ^{\gamma _{k+\ell }}.}
7983:
7962:
7815:
7811:
4189:
1598:
946:
649:
251:
95:
5918:
4017:. It is the smallest ordinal that does not have a finite arithmetical expression in terms of
3751:
3429:
762:
7923:
5938:
5331:
5272:
should be replaced by its factorization into a non-increasing sequence of finite primes and
4897:
3008:
1947:
The definition of exponentiation can also be given by transfinite recursion on the exponent
1752:
58:. Each can be defined in essentially two different ways: either by constructing an explicit
8008:
4865:
4811:
8004:
7676:
7346:
7317:
7256:
3105:
330:
5058:
This prime factorization can easily be read off using the Cantor normal form as follows:
2189:
can be viewed as the order type of finite sequences of natural numbers; every element of
6301:{\displaystyle \alpha +\beta =\omega ^{\omega ^{\omega }}+\omega ^{\omega }+\omega ^{5}}
4531:{\displaystyle 0<\alpha =\omega ^{\beta _{1}}c_{1}+\cdots +\omega ^{\beta _{k}}c_{k}}
3744:
The Cantor normal form allows us to uniquely express—and order—the ordinals
1300:, showing that multiplication of ordinals is not in general commutative, c.f. pictures.
7289:
7269:
6770:{\displaystyle \underbrace {\alpha \oplus \cdots \oplus \alpha } _{n}=\alpha \otimes n}
2827:
Ordinal exponentiation is strictly increasing and continuous in the right argument: If
1814:
1810:
1748:
1511:
55:
51:
43:
7810:. Three common operations on nimbers are nimber addition, nimber multiplication, and
4195:: that is, Peano's axioms can show transfinite induction up to any ordinal less than ε
3632:{\displaystyle \omega ^{\beta _{1}}+\omega ^{\beta _{2}}+\cdots +\omega ^{\beta _{k}}}
2491:{\displaystyle \alpha ^{b_{1}}a_{1}+\alpha ^{b_{2}}a_{2}+\cdots +\alpha ^{b_{k}}a_{k}}
2304:{\displaystyle \omega ^{n_{1}}c_{1}+\omega ^{n_{2}}c_{2}+\cdots +\omega ^{n_{k}}c_{k}}
1155:{\displaystyle \alpha \cdot \beta =\bigcup _{\delta <\beta }(\alpha \cdot \delta )}
592:
but the analogous relation does not hold for the left argument; instead we only have:
8031:
7975:
7858:
7531:
7520:
are both subsets of some larger total order; then their union has order type at most
7087:
Natural sum and product are not continuous in the right argument, since, for example
2180:
2102:{\displaystyle \alpha ^{\beta }=\bigcup _{0<\delta <\beta }(\alpha ^{\delta })}
1740:
1652:
681:
322:
7460:. One may take this relation as a definition of the natural operations by choosing
4184:
is important for various reasons in arithmetic (essentially because it measures the
3859:
and so on recursively, we get a system of notation for these ordinals (for example,
7862:
7311:
4192:
5371:
The operations of addition, multiplication and exponentiation are all examples of
930:, under lexicographic order with least significant position first, has order type
883:, using lexicographic order with least significant position first, has order type
845:
17:
5801:{\displaystyle \alpha _{1},\ldots ,\alpha _{k},\beta _{1},\ldots ,\beta _{\ell }}
7952:
7715:
Under natural addition, the ordinals can be identified with the elements of the
7248:
898:
495:
424:
31:
1389:. Multiplication is strictly increasing and continuous in the right argument: (
990:
The definition of multiplication can also be given by transfinite recursion on
638:{\displaystyle \alpha <\beta \Rightarrow \alpha +\gamma \leq \beta +\gamma }
7307:
971:
that puts the least significant position first. Effectively, each element of
582:{\displaystyle \alpha <\beta \Rightarrow \gamma +\alpha <\gamma +\beta }
488:
59:
35:
5347:. There are other ordinal notations capable of capturing ordinals well past ε
5579:{\displaystyle \beta =\omega ^{\beta _{1}}+\cdots +\omega ^{\beta _{\ell }}}
4296:{\displaystyle \omega ^{\beta }c+\omega ^{\beta '}c'=\omega ^{\beta '}c'\,,}
3097:
3093:
2162:
But for infinite exponents, the definition may not be obvious. For example,
1656:
310:{\displaystyle \alpha +\beta =\bigcup _{\delta <\beta }(\alpha +\delta )}
7927:
5513:{\displaystyle \alpha =\omega ^{\alpha _{1}}+\cdots +\omega ^{\alpha _{k}}}
3701:{\displaystyle \beta _{1}\geq \beta _{2}\geq \ldots \geq \beta _{k}\geq 0}
7726:
3101:
1815:
Von
Neumann's definition of an ordinal as the set of all smaller ordinals
47:
7708:(the usual product), but this is also the natural product of 2 and
2619:
While the same exponent-notation is used for ordinal exponentiation and
4632:{\displaystyle \alpha \omega ^{\beta '}=\omega ^{\beta _{1}+\beta '}\,}
3351:{\displaystyle \beta _{1}>\beta _{2}>\ldots >\beta _{k}\geq 0}
123:
keep the order they already have, and likewise for comparisons within
7807:
7801:
4991:. These are the infinite successor primes, and are the successors of
4781:
To compare two ordinals written in Cantor normal form, first compare
7077:{\displaystyle \alpha \otimes \beta <\omega ^{\omega ^{\gamma }}}
1428:
strictly increasing in the left argument, for example, 1 < 2 but
7918:
7565:, as the smallest ordinal strictly greater than the natural sum of
7211:{\displaystyle \lim _{n<\omega }\alpha \otimes n=\alpha \omega }
7134:{\displaystyle \lim _{n<\omega }\alpha \oplus n=\alpha +\omega }
5149:
is a product of a smaller ordinal and a prime and a natural number
4368:
one can apply the distributive law on the left and rewrite this as
333:
is the same as standard addition. The first transfinite ordinal is
5210:
into a minimal product of infinite primes and natural numbers is
7842:
Ernst
Jacobsthal, Vertauschbarkeit transfiniter Ordnungszahlen,
7693:(the usual sum), but this is also the natural sum of 1 and
6617:{\displaystyle \alpha \otimes \gamma \leq \beta \otimes \gamma }
4974:, the transfinite ordinals that are closed under multiplication.
2168:
can be identified with a set of finite sequences of elements of
380:
0 < 1 < 2 < 3 < ... < 0' < 1' < 2' < ...
6707:{\displaystyle \alpha \otimes \gamma <\beta \otimes \gamma }
7958:
Set Theory: The Third
Millennium Edition, revised and expanded
5321:
As discussed above, the Cantor normal form of ordinals below ε
3828:
in Cantor normal form, and making the same assumption for the
2002:. Writing the successor and limit ordinals cases separately:
1791:. These consist of the ordinal 2 and the ordinals of the form
1054:. Writing the successor and limit ordinals cases separately:
204:. Writing the successor and limit ordinals cases separately:
6553:{\displaystyle \alpha \oplus \gamma <\beta \oplus \gamma }
3801:
in the Cantor normal form, we can also express the exponents
1944:. This is a well-ordering and hence gives an ordinal number.
4970:. These are the prime ordinals that are limits, and are the
6105:{\displaystyle \alpha =\omega ^{\omega ^{\omega }}+\omega }
4061:{\displaystyle \varepsilon _{0}=\omega ^{\varepsilon _{0}}}
94:
with least significant position first, on the union of the
8022:
6951:{\displaystyle \alpha \oplus \beta <\omega ^{\gamma }}
5671:{\displaystyle \beta _{1}\geq \cdots \geq \beta _{\ell }}
5339:
ordinal expressions, and can express all ordinals below ε
3711:
Another variation of the Cantor normal form is the "base
186:
is the smallest ordinal strictly greater than the sum of
5454:
The natural sum and product are defined as follows. Let
62:
that represents the result of the operation or by using
7899:"Intermediate arithmetic operations on ordinal numbers"
7861:
and R. Parikh, Well-partial orderings and hierarchies,
6846:{\displaystyle \alpha \beta \leq \alpha \otimes \beta }
6811:{\displaystyle \alpha +\beta \leq \alpha \oplus \beta }
5625:{\displaystyle \alpha _{1}\geq \cdots \geq \alpha _{k}}
5364:) that are not expressible. Such ordinals are known as
5161:
So the factorization of the Cantor normal form ordinal
5051:
Every limit prime must occur before any successor prime
2117:
Both definitions simplify considerably if the exponent
712:. On the other hand, right cancellation does not work:
27:
Operations on ordinals that extend classical arithmetic
6991:{\displaystyle \alpha <\omega ^{\omega ^{\gamma }}}
4999:
Factorization into primes is not unique: for example,
7422:
7378:
7349:
7320:
7292:
7272:
7224:
7173:
7147:
7093:
7044:
7031:{\displaystyle \beta <\omega ^{\omega ^{\gamma }}}
7004:
6964:
6925:
6892:
6859:
6824:
6786:
6723:
6682:
6656:
6630:
6592:
6566:
6528:
6502:
6424:
6314:
6242:
6164:
6118:
6072:
5961:
5941:
5921:
5840:
5814:
5736:
5723:{\displaystyle \gamma _{1},\ldots ,\gamma _{k+\ell }}
5684:
5638:
5592:
5526:
5460:
4868:
4841:
4814:
4787:
4651:
4578:
4544:
4452:
4421:
4374:
4343:
4312:
4223:
4077:
4027:
3868:
3834:
3807:
3774:
3754:
3649:
3565:
3518:
3485:
3452:
3432:
3405:
3299:
3240:
3126:
2669:
2394:
2207:
2047:
1108:
765:
721:
601:
545:
263:
6151:{\displaystyle \beta =\omega ^{\omega }+\omega ^{5}}
1866:
with the least significant position first: we write
1858:(essentially, we consider the functions with finite
2629:is defined to be the cardinal number of the set of
7980:Set Theory: An Introduction to Independence Proofs
7452:
7408:
7364:
7335:
7298:
7278:
7236:
7210:
7159:
7133:
7076:
7030:
6990:
6950:
6911:
6878:
6845:
6810:
6769:
6706:
6668:
6642:
6616:
6578:
6552:
6514:
6485:
6410:
6300:
6228:
6150:
6104:
6058:
5947:
5927:
5907:
5826:
5800:
5722:
5670:
5624:
5578:
5512:
4881:
4854:
4827:
4800:
4763:
4631:
4561:
4530:
4438:
4407:
4360:
4329:
4295:
4169:
4060:
3976:
3847:
3820:
3793:
3760:
3700:
3631:
3537:
3504:
3471:
3438:
3418:
3350:
3285:
3222:
2682:
2490:
2303:
2101:
1154:
777:
751:
637:
581:
309:
1982:is the smallest ordinal greater than or equal to
1443:. However, it is (non-strictly) increasing, i.e.
1029:is the smallest ordinal greater than or equal to
7262:The natural operations come up in the theory of
7175:
7095:
5391:operations on ordinals were defined in 1906 by
2663:) in the former and symbols for cardinals (e.g.
466:0 < 1 < 2 < ... < 0' < 1' < 2'
447:0 < 1 < 2 < 0' < 1' < 2' < ...
7601:. Similarly, we can define the natural product
4953:, ... There are three sorts of prime ordinals:
2376:The same is true in general: every element of
1813:via order types is most easily explained using
7814:. Nimber addition is a generalization of the
2566:. This expression corresponds to the function
1347:. The ordinal 1 is a multiplicative identity,
1170:As an example, here is the order relation for
831:). These are exactly the ordinals of the form
819:are closed under addition and contain 0, then
337:, the set of all natural numbers, followed by
7881:48 (1942), 262–271. See Theorem 1. Available
7822:of a set of ordinals is the smallest ordinal
1536:. However, the distributive law on the right
8:
6879:{\displaystyle \alpha <\omega ^{\gamma }}
5097:in Cantor normal form gives an expansion of
4901:changing the order of finite prime factors (
2877:. Note, for instance, that 2 < 3 and yet
1710:. Right division does not work: there is no
397:does not have a direct predecessor while in
6912:{\displaystyle \beta <\omega ^{\gamma }}
1274:and after relabeling, this looks just like
752:{\displaystyle 3+\omega =0+\omega =\omega }
90:is the ordinal representing the variant of
7416:, while the type of the direct product is
5400:
4902:
7961:. Springer Science & Business Media.
7917:
7611:by simultaneous transfinite recursion on
7557:by simultaneous transfinite recursion on
7421:
7377:
7348:
7319:
7291:
7271:
7223:
7178:
7172:
7146:
7098:
7092:
7066:
7061:
7043:
7020:
7015:
7003:
6980:
6975:
6963:
6942:
6924:
6903:
6891:
6870:
6858:
6823:
6785:
6749:
6725:
6722:
6681:
6655:
6629:
6591:
6565:
6527:
6501:
6469:
6464:
6443:
6438:
6423:
6402:
6383:
6362:
6357:
6336:
6331:
6313:
6292:
6279:
6264:
6259:
6241:
6214:
6201:
6186:
6181:
6163:
6142:
6129:
6117:
6088:
6083:
6071:
6045:
6032:
6027:
5978:
5960:
5940:
5920:
5888:
5883:
5862:
5857:
5839:
5813:
5792:
5773:
5760:
5741:
5735:
5708:
5689:
5683:
5662:
5643:
5637:
5616:
5597:
5591:
5568:
5563:
5542:
5537:
5525:
5502:
5497:
5476:
5471:
5459:
4995:, the additively indecomposable ordinals.
4873:
4867:
4846:
4840:
4819:
4813:
4792:
4786:
4757:
4751:
4739:
4734:
4715:
4703:
4698:
4682:
4670:
4665:
4650:
4628:
4609:
4604:
4586:
4577:
4543:
4522:
4510:
4505:
4486:
4474:
4469:
4451:
4420:
4379:
4373:
4342:
4311:
4289:
4270:
4244:
4228:
4222:
4163:
4159:
4148:
4143:
4138:
4129:
4124:
4115:
4104:
4095:
4084:
4076:
4050:
4045:
4032:
4026:
3954:
3949:
3922:
3883:
3878:
3873:
3867:
3839:
3833:
3812:
3806:
3779:
3773:
3753:
3686:
3667:
3654:
3648:
3621:
3616:
3595:
3590:
3575:
3570:
3564:
3538:{\displaystyle \alpha =\omega ^{\alpha }}
3529:
3517:
3490:
3484:
3457:
3451:
3431:
3410:
3404:
3358:are ordinal numbers. The degenerate case
3336:
3317:
3304:
3298:
3286:{\displaystyle c_{1},c_{2},\ldots ,c_{k}}
3277:
3258:
3245:
3239:
3214:
3202:
3197:
3178:
3166:
3161:
3148:
3136:
3131:
3125:
2674:
2668:
2482:
2470:
2465:
2446:
2434:
2429:
2416:
2404:
2399:
2393:
2295:
2283:
2278:
2259:
2247:
2242:
2229:
2217:
2212:
2206:
2090:
2065:
2052:
2046:
1817:. Then, to construct a set of order type
1636:. Right cancellation does not work, e.g.
1125:
1107:
764:
720:
600:
544:
280:
262:
7892:
7890:
7534:, then their sum has order type at most
7512:. A useful application of this is when
897:
844:
798:: for example, there does not exist any
42:describes the three usual operations on
7835:
1764:Multiplicatively indecomposable ordinal
67:
7237:{\displaystyle \alpha \otimes \omega }
5104:Now look at the Cantor normal form of
4408:{\displaystyle \omega ^{\beta }(c+c')}
3472:{\displaystyle \beta _{1}\leq \alpha }
2388:) can be uniquely written in the form
2201:) can be uniquely written in the form
788:Nor does right subtraction, even when
71:
7160:{\displaystyle \alpha \oplus \omega }
5373:primitive recursive ordinal functions
5062:First write the ordinal as a product
4021:, and the smallest ordinal such that
3794:{\displaystyle \beta _{1}<\alpha }
423:Ordinal addition is, in general, not
7:
7530:. If they are both subsets of some
7372:, the type of the disjoint union is
5827:{\displaystyle \alpha \oplus \beta }
5808:sorted in nonincreasing order. Then
967:can be well-ordered by a variant of
7846:, Bd 64 (1907), 475-488. Available
7818:operation on natural numbers. The
7547:We can also define the natural sum
4211:
2643:, while the ordinal exponentiation
1848:for all but finitely many elements
6579:{\displaystyle \alpha \leq \beta }
3505:{\displaystyle \beta _{1}=\alpha }
3011:showed that the only solutions of
2671:
2562:are nonzero ordinals smaller than
1823:consider the set of all functions
975:is replaced by a disjoint copy of
25:
6643:{\displaystyle \alpha <\beta }
6515:{\displaystyle \alpha <\beta }
4439:{\displaystyle \beta '<\beta }
4330:{\displaystyle \beta '>\beta }
3392:, and can be considered the base-
3293:are nonzero natural numbers, and
2382:(i.e. every ordinal smaller than
2355:are nonzero natural numbers, and
2195:(i.e. every ordinal smaller than
2172:, properly ordered. The equation
1597:, which is different. There is a
1492:for some nonzero natural numbers
1361:. Multiplication is associative,
1217:which has the same order type as
829:additively indecomposable ordinal
415:do not have direct predecessors.
115:is smaller than every element of
82:The sum of two well-ordered sets
7453:{\displaystyle o(S)\otimes o(T)}
7266:; given two well partial orders
5395:, and are sometimes called the
2612:and sends all other elements of
1958:, ordinary exponentiation gives
1739:The ordinal numbers form a left
1001:, ordinary multiplication gives
68:"natural" arithmetic of ordinals
7729:generated by the delta numbers
7719:generated by the gamma numbers
7409:{\displaystyle o(S)\oplus o(T)}
5586:be in Cantor normal form (i.e.
3998:) is the set of ordinal values
3737:are nonzero ordinals less than
1751:. Hence the ordinals are not a
1651:, but 1 and 2 are different. A
498:; one can see for example that
468:has a largest element (namely,
7865:39 (1977), 195–206. Available
7447:
7441:
7432:
7426:
7403:
7397:
7388:
7382:
7359:
7353:
7330:
7324:
5076:in the Cantor normal form and
4957:The finite primes 2, 3, 5, ...
4778:is a non-zero natural number.
4402:
4385:
4361:{\displaystyle \beta '=\beta }
2096:
2083:
1149:
1137:
680:. Furthermore, one can define
611:
555:
491:, but not order isomorphic).
304:
292:
111:. This way, every element of
1:
5431:, and the natural product by
5101:as a product of limit primes.
4538:is in Cantor normal form and
4207:
2127:is then just the product of
438:since the order relation for
8000:Cardinal and ordinal numbers
7906:Mathematical Logic Quarterly
7897:Altman, Harry (2017-11-01).
6669:{\displaystyle \gamma >0}
4562:{\displaystyle 0<\beta '}
2649:only contains the functions
1876:if and only if there exists
449:, which can be relabeled to
7675:. Also, see the article on
3768:: in other words, assuming
3719:is replaced by any ordinal
3120:can be uniquely written as
2683:{\displaystyle \aleph _{0}}
959:, of two well-ordered sets
363:0' < 1' < 2' < ...
130:The definition of addition
8059:
8023:ordCalc ordinal calculator
7799:
7739:is any delta number, then
7619:, as the smallest ordinal
4855:{\displaystyle \beta _{2}}
4801:{\displaystyle \beta _{1}}
3848:{\displaystyle \beta _{i}}
3821:{\displaystyle \beta _{i}}
3419:{\displaystyle \beta _{1}}
2522:are ordinals smaller than
2028:, for a successor ordinal
1089:, for a successor ordinal
815:If the ordinals less than
494:Ordinal addition is still
155:, ordinary addition gives
7727:free commutative semiring
5362:first uncountable ordinal
5072:is the smallest power of
4977:The ordinals of the form
4960:The ordinals of the form
4893:Factorization into primes
3643:is a natural number, and
3397:positional numeral system
3380:s. This decomposition of
3059:is any limit ordinal and
1864:ordered lexicographically
1770:greater than 1 such that
890:. This is different from
823:is occasionally called a
464:since the order relation
148:. When the right addend
7812:minimum excludance (mex)
5366:large countable ordinals
5317:Large countable ordinals
4186:proof-theoretic strength
3426:is called the degree of
3399:. The highest exponent
2953:then there exist unique
1674:, then there are unique
1659:property holds: for all
994:. When the right factor
329:Ordinal addition on the
7717:free commutative monoid
5928:{\displaystyle \alpha }
5915:The natural product of
5403:). The natural sum of
3761:{\displaystyle \omega }
3512:applies if and only if
3439:{\displaystyle \alpha }
2621:cardinal exponentiation
1482:commute if and only if
778:{\displaystyle 3\neq 0}
536:in the right argument:
385:This is different from
7928:10.1002/malq.201600006
7879:Bull. Amer. Math. Soc.
7454:
7410:
7366:
7337:
7300:
7280:
7238:
7212:
7161:
7135:
7078:
7032:
6992:
6952:
6913:
6880:
6847:
6812:
6771:
6708:
6670:
6644:
6618:
6580:
6554:
6516:
6487:
6412:
6302:
6230:
6152:
6106:
6060:
5949:
5948:{\displaystyle \beta }
5929:
5909:
5828:
5802:
5724:
5672:
5626:
5580:
5514:
5343:, but cannot express ε
5128:+ smaller terms, then
4883:
4856:
4829:
4802:
4765:
4633:
4563:
4532:
4440:
4409:
4362:
4331:
4297:
4171:
4062:
3978:
3849:
3822:
3795:
3762:
3702:
3633:
3539:
3506:
3473:
3440:
3420:
3352:
3287:
3224:
2684:
2492:
2305:
2153:, and the elements of
2103:
1156:
942:
895:
779:
753:
639:
583:
311:
7844:Mathematische Annalen
7532:ordered abelian group
7455:
7411:
7367:
7338:
7301:
7281:
7239:
7213:
7162:
7136:
7079:
7033:
6993:
6953:
6914:
6881:
6848:
6813:
6772:
6709:
6671:
6645:
6619:
6581:
6555:
6517:
6488:
6413:
6303:
6231:
6153:
6107:
6066:For example, suppose
6061:
5950:
5930:
5910:
5829:
5803:
5725:
5673:
5627:
5581:
5515:
5411:is often denoted by
4884:
4882:{\displaystyle c_{2}}
4857:
4830:
4828:{\displaystyle c_{1}}
4803:
4766:
4634:
4564:
4533:
4441:
4410:
4363:
4332:
4298:
4212:§ Multiplication
4172:
4063:
3987:denotes an ordinal).
3979:
3850:
3823:
3796:
3763:
3708:are ordinal numbers.
3703:
3634:
3540:
3507:
3474:
3441:
3421:
3353:
3288:
3234:is a natural number,
3225:
3116:Every ordinal number
3088:Beyond exponentiation
2928:this is not the case.
2685:
2502:is a natural number,
2493:
2335:are natural numbers,
2306:
2104:
1323:zero-product property
1157:
969:lexicographical order
901:
848:
780:
754:
640:
584:
365:for the second copy,
312:
142:transfinite recursion
140:can also be given by
119:, comparisons within
92:lexicographical order
64:transfinite recursion
7826:present in the set.
7816:bitwise exclusive or
7420:
7376:
7365:{\displaystyle o(T)}
7347:
7336:{\displaystyle o(S)}
7318:
7290:
7270:
7222:
7171:
7145:
7091:
7042:
7002:
6962:
6923:
6890:
6857:
6822:
6784:
6721:
6680:
6654:
6628:
6590:
6564:
6526:
6500:
6422:
6312:
6240:
6162:
6116:
6070:
5959:
5939:
5919:
5838:
5812:
5734:
5682:
5636:
5590:
5524:
5458:
4866:
4839:
4812:
4785:
4649:
4576:
4542:
4450:
4419:
4372:
4341:
4310:
4221:
4075:
4025:
3866:
3832:
3805:
3772:
3752:
3647:
3563:
3516:
3483:
3450:
3430:
3403:
3297:
3238:
3124:
2667:
2392:
2205:
2183:system. The ordinal
2121:is a finite number:
2045:
1951:. When the exponent
1514:holds, on the left:
1424:. Multiplication is
1106:
937:, which is equal to
763:
719:
694:: there is a unique
648:Ordinal addition is
599:
543:
261:
7264:well partial orders
2113:is a limit ordinal.
1166:is a limit ordinal.
849:The disjoint union
530:strictly increasing
351:, etc. The ordinal
7995:Sierpiński, Wacław
7450:
7406:
7362:
7333:
7296:
7276:
7234:
7208:
7189:
7157:
7131:
7109:
7074:
7028:
6988:
6948:
6909:
6876:
6843:
6808:
6767:
6754:
6747:
6704:
6666:
6640:
6614:
6576:
6550:
6512:
6483:
6408:
6298:
6226:
6148:
6102:
6056:
6022:
6020:
5945:
5925:
5905:
5824:
5798:
5720:
5668:
5622:
5576:
5510:
5393:Gerhard Hessenberg
5379:Natural operations
4879:
4852:
4825:
4798:
4761:
4629:
4559:
4528:
4436:
4405:
4358:
4327:
4293:
4167:
4058:
3974:
3845:
3818:
3791:
3758:
3726:, and the numbers
3715:expansion", where
3698:
3629:
3535:
3502:
3469:
3436:
3416:
3386:Cantor normal form
3348:
3283:
3220:
3112:Cantor normal form
2680:
2488:
2301:
2099:
2082:
1809:The definition of
1152:
1136:
943:
896:
775:
749:
635:
579:
307:
291:
96:Cartesian products
40:ordinal arithmetic
18:Cantor normal form
7968:978-3-540-44085-7
7955:(21 March 2006).
7859:D. H. J. De Jongh
7796:Nimber arithmetic
7299:{\displaystyle T}
7279:{\displaystyle S}
7174:
7094:
6726:
6724:
5974:
5730:be the exponents
5140:+ smaller terms)(
3372:and there are no
2690:) in the latter.
2061:
1599:left cancellation
1234:looks like this:
1121:
947:Cartesian product
650:left-cancellative
407:the two elements
276:
72:nimber operations
16:(Redirected from
8050:
8011:
7972:
7938:
7937:
7935:
7934:
7921:
7903:
7894:
7885:
7875:
7869:
7856:
7850:
7840:
7821:
7788:
7738:
7734:
7724:
7711:
7707:
7700:
7696:
7692:
7685:
7674:
7664:
7654:
7622:
7618:
7614:
7610:
7600:
7590:
7586:
7582:
7572:
7568:
7564:
7560:
7556:
7543:
7529:
7519:
7515:
7511:
7507:
7503:
7493:
7489:
7485:
7475:
7471:
7467:
7463:
7459:
7457:
7456:
7451:
7415:
7413:
7412:
7407:
7371:
7369:
7368:
7363:
7342:
7340:
7339:
7334:
7305:
7303:
7302:
7297:
7285:
7283:
7282:
7277:
7243:
7241:
7240:
7235:
7217:
7215:
7214:
7209:
7188:
7166:
7164:
7163:
7158:
7140:
7138:
7137:
7132:
7108:
7083:
7081:
7080:
7075:
7073:
7072:
7071:
7070:
7037:
7035:
7034:
7029:
7027:
7026:
7025:
7024:
6997:
6995:
6994:
6989:
6987:
6986:
6985:
6984:
6957:
6955:
6954:
6949:
6947:
6946:
6918:
6916:
6915:
6910:
6908:
6907:
6885:
6883:
6882:
6877:
6875:
6874:
6852:
6850:
6849:
6844:
6817:
6815:
6814:
6809:
6776:
6774:
6773:
6768:
6753:
6748:
6743:
6713:
6711:
6710:
6705:
6675:
6673:
6672:
6667:
6649:
6647:
6646:
6641:
6623:
6621:
6620:
6615:
6585:
6583:
6582:
6577:
6559:
6557:
6556:
6551:
6521:
6519:
6518:
6513:
6492:
6490:
6489:
6484:
6482:
6481:
6474:
6473:
6456:
6455:
6448:
6447:
6417:
6415:
6414:
6409:
6407:
6406:
6394:
6393:
6375:
6374:
6367:
6366:
6349:
6348:
6341:
6340:
6307:
6305:
6304:
6299:
6297:
6296:
6284:
6283:
6271:
6270:
6269:
6268:
6235:
6233:
6232:
6227:
6219:
6218:
6206:
6205:
6193:
6192:
6191:
6190:
6157:
6155:
6154:
6149:
6147:
6146:
6134:
6133:
6111:
6109:
6108:
6103:
6095:
6094:
6093:
6092:
6065:
6063:
6062:
6057:
6052:
6051:
6050:
6049:
6037:
6036:
6021:
6001:
5981:
5954:
5952:
5951:
5946:
5934:
5932:
5931:
5926:
5914:
5912:
5911:
5906:
5901:
5900:
5899:
5898:
5869:
5868:
5867:
5866:
5833:
5831:
5830:
5825:
5807:
5805:
5804:
5799:
5797:
5796:
5778:
5777:
5765:
5764:
5746:
5745:
5729:
5727:
5726:
5721:
5719:
5718:
5694:
5693:
5677:
5675:
5674:
5669:
5667:
5666:
5648:
5647:
5631:
5629:
5628:
5623:
5621:
5620:
5602:
5601:
5585:
5583:
5582:
5577:
5575:
5574:
5573:
5572:
5549:
5548:
5547:
5546:
5519:
5517:
5516:
5511:
5509:
5508:
5507:
5506:
5483:
5482:
5481:
5480:
5450:
5440:
5430:
5420:
5410:
5406:
5359:
5332:ordinal notation
5328:
5311:
5293:
5271:
5257:
5205:
5187:
5156:
5152:
5148:
5127:
5107:
5100:
5096:
5092:
5079:
5075:
5071:
5067:
5046:
5032:
5013:
5002:
4990:
4984:for any ordinal
4983:
4969:
4966:for any ordinal
4965:
4952:
4945:
4938:
4932:
4925:
4918:
4911:
4898:Ernst Jacobsthal
4888:
4886:
4885:
4880:
4878:
4877:
4861:
4859:
4858:
4853:
4851:
4850:
4834:
4832:
4831:
4826:
4824:
4823:
4807:
4805:
4804:
4799:
4797:
4796:
4777:
4770:
4768:
4767:
4762:
4756:
4755:
4746:
4745:
4744:
4743:
4720:
4719:
4710:
4709:
4708:
4707:
4687:
4686:
4677:
4676:
4675:
4674:
4638:
4636:
4635:
4630:
4627:
4626:
4625:
4614:
4613:
4596:
4595:
4594:
4568:
4566:
4565:
4560:
4558:
4537:
4535:
4534:
4529:
4527:
4526:
4517:
4516:
4515:
4514:
4491:
4490:
4481:
4480:
4479:
4478:
4445:
4443:
4442:
4437:
4429:
4414:
4412:
4411:
4406:
4401:
4384:
4383:
4367:
4365:
4364:
4359:
4351:
4336:
4334:
4333:
4328:
4320:
4302:
4300:
4299:
4294:
4288:
4280:
4279:
4278:
4262:
4254:
4253:
4252:
4233:
4232:
4193:Peano arithmetic
4176:
4174:
4173:
4168:
4155:
4154:
4153:
4152:
4134:
4133:
4120:
4119:
4100:
4099:
4067:
4065:
4064:
4059:
4057:
4056:
4055:
4054:
4037:
4036:
4020:
3983:
3981:
3980:
3975:
3961:
3960:
3959:
3958:
3935:
3934:
3927:
3926:
3908:
3907:
3888:
3887:
3858:
3854:
3852:
3851:
3846:
3844:
3843:
3827:
3825:
3824:
3819:
3817:
3816:
3800:
3798:
3797:
3792:
3784:
3783:
3767:
3765:
3764:
3759:
3747:
3740:
3736:
3725:
3718:
3714:
3707:
3705:
3704:
3699:
3691:
3690:
3672:
3671:
3659:
3658:
3642:
3638:
3636:
3635:
3630:
3628:
3627:
3626:
3625:
3602:
3601:
3600:
3599:
3582:
3581:
3580:
3579:
3558:
3544:
3542:
3541:
3536:
3534:
3533:
3511:
3509:
3508:
3503:
3495:
3494:
3478:
3476:
3475:
3470:
3462:
3461:
3446:, and satisfies
3445:
3443:
3442:
3437:
3425:
3423:
3422:
3417:
3415:
3414:
3395:
3391:
3383:
3379:
3375:
3371:
3364:
3357:
3355:
3354:
3349:
3341:
3340:
3322:
3321:
3309:
3308:
3292:
3290:
3289:
3284:
3282:
3281:
3263:
3262:
3250:
3249:
3233:
3229:
3227:
3226:
3221:
3219:
3218:
3209:
3208:
3207:
3206:
3183:
3182:
3173:
3172:
3171:
3170:
3153:
3152:
3143:
3142:
3141:
3140:
3119:
3083:
3077:
3072:
3068:
3058:
3054:
3047:
3040:
3030:
3020:
3003:
2993:
2982:
2964:
2960:
2956:
2952:
2945:
2938:
2934:
2927:
2920:
2913:
2903:
2893:
2883:
2876:
2866:
2853:
2843:
2833:
2823:
2800:. For instance,
2799:
2780:
2776:
2772:
2765:
2752:
2736:
2724:
2718:
2714:
2704:
2689:
2687:
2686:
2681:
2679:
2678:
2662:
2658:
2648:
2642:
2628:
2615:
2611:
2601:
2590:
2579:
2565:
2561:
2543:
2525:
2521:
2510:
2501:
2497:
2495:
2494:
2489:
2487:
2486:
2477:
2476:
2475:
2474:
2451:
2450:
2441:
2440:
2439:
2438:
2421:
2420:
2411:
2410:
2409:
2408:
2387:
2381:
2372:
2354:
2343:
2334:
2323:
2314:
2310:
2308:
2307:
2302:
2300:
2299:
2290:
2289:
2288:
2287:
2264:
2263:
2254:
2253:
2252:
2251:
2234:
2233:
2224:
2223:
2222:
2221:
2200:
2194:
2188:
2178:
2171:
2167:
2158:
2152:
2134:
2130:
2126:
2120:
2112:
2108:
2106:
2105:
2100:
2095:
2094:
2081:
2057:
2056:
2038:
2027:
2011:
2001:
1991:
1981:
1975:
1968:
1964:
1957:
1950:
1943:
1933:
1923:
1904:
1885:
1875:
1862:). This set is
1857:
1847:
1836:
1822:
1800:
1790:
1779:
1769:
1766:) is an ordinal
1761:
1753:Euclidean domain
1735:
1713:
1709:
1699:
1681:
1677:
1673:
1666:
1662:
1650:
1635:
1625:
1607:
1596:
1577:
1563:generally true:
1558:
1535:
1507:
1503:
1500:. The relation "
1499:
1495:
1491:
1481:
1477:
1470:
1452:
1442:
1423:
1405:
1398:
1388:
1360:
1346:
1339:
1320:
1299:
1277:
1233:
1226:
1176:
1165:
1161:
1159:
1158:
1153:
1135:
1099:
1088:
1060:
1053:
1043:
1028:
1018:
1011:
1007:
1000:
993:
986:
982:
978:
974:
966:
962:
958:
940:
936:
929:
919:
911:
893:
889:
882:
881:
865:
836:
826:
822:
818:
811:
801:
797:
784:
782:
781:
776:
758:
756:
755:
750:
711:
697:
693:
682:left subtraction
679:
669:
644:
642:
641:
636:
588:
586:
585:
580:
524:
486:
479:
475:
471:
467:
463:
460:is not equal to
459:
452:
448:
444:
437:
414:
410:
406:
396:
392:
388:
381:
374:
364:
360:
350:
343:
336:
320:
316:
314:
313:
308:
290:
248:
244:
216:
203:
193:
189:
185:
175:
168:
164:
154:
147:
139:
126:
122:
118:
114:
110:
103:
89:
85:
60:well-ordered set
21:
8058:
8057:
8053:
8052:
8051:
8049:
8048:
8047:
8043:Ordinal numbers
8028:
8027:
8019:
8014:
7993:
7969:
7951:
7947:
7942:
7941:
7932:
7930:
7912:(3–4): 228–42.
7901:
7896:
7895:
7888:
7876:
7872:
7857:
7853:
7841:
7837:
7832:
7819:
7804:
7798:
7743:
7736:
7730:
7720:
7709:
7702:
7698:
7694:
7687:
7683:
7677:surreal numbers
7666:
7656:
7624:
7620:
7616:
7612:
7602:
7592:
7588:
7584:
7574:
7570:
7566:
7562:
7558:
7548:
7535:
7521:
7517:
7513:
7509:
7505:
7495:
7491:
7487:
7477:
7473:
7469:
7468:to be ordinals
7465:
7461:
7418:
7417:
7374:
7373:
7345:
7344:
7316:
7315:
7288:
7287:
7268:
7267:
7257:surreal numbers
7220:
7219:
7169:
7168:
7143:
7142:
7089:
7088:
7062:
7057:
7040:
7039:
7016:
7011:
7000:
6999:
6976:
6971:
6960:
6959:
6938:
6921:
6920:
6899:
6888:
6887:
6866:
6855:
6854:
6820:
6819:
6782:
6781:
6780:We always have
6727:
6719:
6718:
6678:
6677:
6652:
6651:
6626:
6625:
6588:
6587:
6562:
6561:
6524:
6523:
6498:
6497:
6465:
6460:
6439:
6434:
6420:
6419:
6398:
6379:
6358:
6353:
6332:
6327:
6310:
6309:
6288:
6275:
6260:
6255:
6238:
6237:
6210:
6197:
6182:
6177:
6160:
6159:
6138:
6125:
6114:
6113:
6084:
6079:
6068:
6067:
6041:
6028:
6023:
6019:
6018:
5999:
5998:
5957:
5956:
5937:
5936:
5917:
5916:
5884:
5879:
5858:
5853:
5836:
5835:
5810:
5809:
5788:
5769:
5756:
5737:
5732:
5731:
5704:
5685:
5680:
5679:
5658:
5639:
5634:
5633:
5612:
5593:
5588:
5587:
5564:
5559:
5538:
5533:
5522:
5521:
5498:
5493:
5472:
5467:
5456:
5455:
5442:
5432:
5422:
5412:
5408:
5404:
5401:Sierpiński 1958
5389:natural product
5381:
5358:
5352:
5350:
5346:
5342:
5326:
5324:
5319:
5310:
5301:
5295:
5284:
5276:
5270:
5262:
5256:
5245:
5231:
5214:
5204:
5195:
5189:
5186:
5174:
5165:
5154:
5150:
5129:
5109:
5105:
5098:
5094:
5084:
5080:is a successor.
5077:
5073:
5069:
5063:
5034:
5015:
5004:
5000:
4985:
4978:
4967:
4961:
4947:
4940:
4934:
4927:
4920:
4913:
4909:
4903:Sierpiński 1958
4895:
4869:
4864:
4863:
4842:
4837:
4836:
4815:
4810:
4809:
4788:
4783:
4782:
4775:
4747:
4735:
4730:
4711:
4699:
4694:
4678:
4666:
4661:
4647:
4646:
4618:
4605:
4600:
4587:
4582:
4574:
4573:
4551:
4540:
4539:
4518:
4506:
4501:
4482:
4470:
4465:
4448:
4447:
4422:
4417:
4416:
4394:
4375:
4370:
4369:
4344:
4339:
4338:
4313:
4308:
4307:
4281:
4271:
4266:
4255:
4245:
4240:
4224:
4219:
4218:
4208:§ Addition
4202:
4199:but not up to ε
4198:
4183:
4144:
4139:
4125:
4111:
4091:
4073:
4072:
4046:
4041:
4028:
4023:
4022:
4018:
4008:
3993:
3950:
3945:
3918:
3879:
3874:
3869:
3864:
3863:
3856:
3835:
3830:
3829:
3808:
3803:
3802:
3775:
3770:
3769:
3750:
3749:
3745:
3738:
3735:
3727:
3720:
3716:
3712:
3682:
3663:
3650:
3645:
3644:
3640:
3617:
3612:
3591:
3586:
3571:
3566:
3561:
3560:
3557:
3549:
3525:
3514:
3513:
3486:
3481:
3480:
3479:. The equality
3453:
3448:
3447:
3428:
3427:
3406:
3401:
3400:
3393:
3389:
3381:
3377:
3373:
3366:
3359:
3332:
3313:
3300:
3295:
3294:
3273:
3254:
3241:
3236:
3235:
3231:
3210:
3198:
3193:
3174:
3162:
3157:
3144:
3132:
3127:
3122:
3121:
3117:
3114:
3106:Veblen function
3090:
3081:
3075:
3070:
3060:
3056:
3049:
3042:
3032:
3022:
3012:
2995:
2984:
2966:
2962:
2958:
2954:
2947:
2940:
2936:
2932:
2922:
2915:
2905:
2895:
2888:
2878:
2868:
2858:
2845:
2835:
2828:
2801:
2782:
2778:
2774:
2770:
2756:
2740:
2728:
2722:
2716:
2709:
2699:
2696:
2670:
2665:
2664:
2660:
2650:
2644:
2634:
2624:
2613:
2603:
2600:
2592:
2589:
2581:
2567:
2563:
2560:
2551:
2545:
2542:
2533:
2527:
2523:
2520:
2512:
2509:
2503:
2499:
2478:
2466:
2461:
2442:
2430:
2425:
2412:
2400:
2395:
2390:
2389:
2383:
2377:
2371:
2362:
2356:
2353:
2345:
2342:
2336:
2333:
2325:
2322:
2316:
2312:
2291:
2279:
2274:
2255:
2243:
2238:
2225:
2213:
2208:
2203:
2202:
2196:
2190:
2184:
2173:
2169:
2163:
2154:
2136:
2132:
2128:
2122:
2118:
2110:
2086:
2048:
2043:
2042:
2029:
2015:
2006:
1993:
1983:
1977:
1976:, the value of
1970:
1966:
1959:
1952:
1948:
1935:
1925:
1906:
1887:
1877:
1867:
1849:
1838:
1824:
1818:
1807:
1792:
1781:
1771:
1767:
1759:
1715:
1711:
1701:
1683:
1679:
1675:
1668:
1664:
1660:
1637:
1627:
1609:
1602:
1579:
1564:
1537:
1515:
1505:
1501:
1497:
1493:
1483:
1479:
1475:
1454:
1444:
1429:
1407:
1400:
1390:
1362:
1348:
1341:
1326:
1311:
1309:
1279:
1275:
1269:
1265:
1261:
1257:
1253:
1249:
1245:
1241:
1228:
1227:. In contrast,
1218:
1212:
1208:
1204:
1200:
1197:< ... < 0
1196:
1192:
1188:
1184:
1171:
1163:
1104:
1103:
1090:
1064:
1058:
1045:
1030:
1020:
1019:, the value of
1013:
1009:
1002:
995:
991:
984:
980:
976:
972:
964:
960:
950:
938:
931:
913:
905:
903:
891:
884:
867:
851:
850:
843:
832:
824:
820:
816:
803:
799:
789:
761:
760:
717:
716:
699:
695:
685:
671:
653:
597:
596:
541:
540:
499:
481:
477:
473:
469:
465:
461:
454:
450:
446:
439:
428:
427:. For example,
421:
412:
408:
398:
394:
390:
386:
379:
366:
362:
352:
345:
338:
334:
331:natural numbers
318:
259:
258:
246:
219:
208:
195:
191:
187:
177:
176:, the value of
170:
166:
156:
149:
145:
131:
124:
120:
116:
112:
105:
98:
87:
83:
80:
44:ordinal numbers
28:
23:
22:
15:
12:
11:
5:
8056:
8054:
8046:
8045:
8040:
8030:
8029:
8026:
8025:
8018:
8017:External links
8015:
8013:
8012:
7991:
7976:Kunen, Kenneth
7973:
7967:
7948:
7946:
7943:
7940:
7939:
7886:
7870:
7851:
7834:
7833:
7831:
7828:
7800:Main article:
7797:
7794:
7790:
7789:
7449:
7446:
7443:
7440:
7437:
7434:
7431:
7428:
7425:
7405:
7402:
7399:
7396:
7393:
7390:
7387:
7384:
7381:
7361:
7358:
7355:
7352:
7332:
7329:
7326:
7323:
7312:linearizations
7295:
7275:
7233:
7230:
7227:
7207:
7204:
7201:
7198:
7195:
7192:
7187:
7184:
7181:
7177:
7156:
7153:
7150:
7130:
7127:
7124:
7121:
7118:
7115:
7112:
7107:
7104:
7101:
7097:
7069:
7065:
7060:
7056:
7053:
7050:
7047:
7023:
7019:
7014:
7010:
7007:
6983:
6979:
6974:
6970:
6967:
6945:
6941:
6937:
6934:
6931:
6928:
6906:
6902:
6898:
6895:
6873:
6869:
6865:
6862:
6842:
6839:
6836:
6833:
6830:
6827:
6807:
6804:
6801:
6798:
6795:
6792:
6789:
6766:
6763:
6760:
6757:
6752:
6746:
6742:
6739:
6736:
6733:
6730:
6703:
6700:
6697:
6694:
6691:
6688:
6685:
6665:
6662:
6659:
6639:
6636:
6633:
6613:
6610:
6607:
6604:
6601:
6598:
6595:
6575:
6572:
6569:
6549:
6546:
6543:
6540:
6537:
6534:
6531:
6511:
6508:
6505:
6480:
6477:
6472:
6468:
6463:
6459:
6454:
6451:
6446:
6442:
6437:
6433:
6430:
6427:
6405:
6401:
6397:
6392:
6389:
6386:
6382:
6378:
6373:
6370:
6365:
6361:
6356:
6352:
6347:
6344:
6339:
6335:
6330:
6326:
6323:
6320:
6317:
6295:
6291:
6287:
6282:
6278:
6274:
6267:
6263:
6258:
6254:
6251:
6248:
6245:
6225:
6222:
6217:
6213:
6209:
6204:
6200:
6196:
6189:
6185:
6180:
6176:
6173:
6170:
6167:
6145:
6141:
6137:
6132:
6128:
6124:
6121:
6101:
6098:
6091:
6087:
6082:
6078:
6075:
6055:
6048:
6044:
6040:
6035:
6031:
6026:
6017:
6014:
6011:
6008:
6005:
6002:
6000:
5997:
5994:
5991:
5988:
5985:
5982:
5980:
5977:
5973:
5970:
5967:
5964:
5955:is defined as
5944:
5924:
5904:
5897:
5894:
5891:
5887:
5882:
5878:
5875:
5872:
5865:
5861:
5856:
5852:
5849:
5846:
5843:
5834:is defined as
5823:
5820:
5817:
5795:
5791:
5787:
5784:
5781:
5776:
5772:
5768:
5763:
5759:
5755:
5752:
5749:
5744:
5740:
5717:
5714:
5711:
5707:
5703:
5700:
5697:
5692:
5688:
5665:
5661:
5657:
5654:
5651:
5646:
5642:
5619:
5615:
5611:
5608:
5605:
5600:
5596:
5571:
5567:
5562:
5558:
5555:
5552:
5545:
5541:
5536:
5532:
5529:
5505:
5501:
5496:
5492:
5489:
5486:
5479:
5475:
5470:
5466:
5463:
5399:(or product) (
5397:Hessenberg sum
5380:
5377:
5356:
5348:
5344:
5340:
5322:
5318:
5315:
5314:
5313:
5306:
5299:
5280:
5266:
5259:
5258:
5254:
5240:
5227:
5208:
5207:
5200:
5193:
5182:
5172:
5159:
5158:
5102:
5081:
5056:
5055:
5052:
4997:
4996:
4975:
4958:
4894:
4891:
4876:
4872:
4849:
4845:
4822:
4818:
4795:
4791:
4772:
4771:
4760:
4754:
4750:
4742:
4738:
4733:
4729:
4726:
4723:
4718:
4714:
4706:
4702:
4697:
4693:
4690:
4685:
4681:
4673:
4669:
4664:
4660:
4657:
4654:
4640:
4639:
4624:
4621:
4617:
4612:
4608:
4603:
4599:
4593:
4590:
4585:
4581:
4557:
4554:
4550:
4547:
4525:
4521:
4513:
4509:
4504:
4500:
4497:
4494:
4489:
4485:
4477:
4473:
4468:
4464:
4461:
4458:
4455:
4435:
4432:
4428:
4425:
4404:
4400:
4397:
4393:
4390:
4387:
4382:
4378:
4357:
4354:
4350:
4347:
4326:
4323:
4319:
4316:
4304:
4303:
4292:
4287:
4284:
4277:
4274:
4269:
4265:
4261:
4258:
4251:
4248:
4243:
4239:
4236:
4231:
4227:
4200:
4196:
4181:
4178:
4177:
4166:
4162:
4158:
4151:
4147:
4142:
4137:
4132:
4128:
4123:
4118:
4114:
4110:
4107:
4103:
4098:
4094:
4090:
4087:
4083:
4080:
4053:
4049:
4044:
4040:
4035:
4031:
4006:
3996:epsilon nought
3991:
3985:
3984:
3973:
3970:
3967:
3964:
3957:
3953:
3948:
3944:
3941:
3938:
3933:
3930:
3925:
3921:
3917:
3914:
3911:
3906:
3903:
3900:
3897:
3894:
3891:
3886:
3882:
3877:
3872:
3842:
3838:
3815:
3811:
3790:
3787:
3782:
3778:
3757:
3731:
3697:
3694:
3689:
3685:
3681:
3678:
3675:
3670:
3666:
3662:
3657:
3653:
3624:
3620:
3615:
3611:
3608:
3605:
3598:
3594:
3589:
3585:
3578:
3574:
3569:
3553:
3532:
3528:
3524:
3521:
3501:
3498:
3493:
3489:
3468:
3465:
3460:
3456:
3435:
3413:
3409:
3384:is called the
3347:
3344:
3339:
3335:
3331:
3328:
3325:
3320:
3316:
3312:
3307:
3303:
3280:
3276:
3272:
3269:
3266:
3261:
3257:
3253:
3248:
3244:
3217:
3213:
3205:
3201:
3196:
3192:
3189:
3186:
3181:
3177:
3169:
3165:
3160:
3156:
3151:
3147:
3139:
3135:
3130:
3113:
3110:
3089:
3086:
3006:
3005:
2929:
2885:
2855:
2825:
2767:
2754:
2738:
2726:
2720:
2706:
2695:
2692:
2677:
2673:
2596:
2585:
2556:
2549:
2538:
2534:> ... >
2531:
2516:
2507:
2485:
2481:
2473:
2469:
2464:
2460:
2457:
2454:
2449:
2445:
2437:
2433:
2428:
2424:
2419:
2415:
2407:
2403:
2398:
2367:
2363:> ... >
2360:
2349:
2340:
2329:
2320:
2298:
2294:
2286:
2282:
2277:
2273:
2270:
2267:
2262:
2258:
2250:
2246:
2241:
2237:
2232:
2228:
2220:
2216:
2211:
2115:
2114:
2098:
2093:
2089:
2085:
2080:
2077:
2074:
2071:
2068:
2064:
2060:
2055:
2051:
2040:
2013:
1811:exponentiation
1806:
1805:Exponentiation
1803:
1512:Distributivity
1504:commutes with
1308:
1305:
1272:
1271:
1267:
1263:
1259:
1255:
1251:
1247:
1243:
1239:
1215:
1214:
1210:
1206:
1202:
1198:
1194:
1190:
1186:
1182:
1168:
1167:
1151:
1148:
1145:
1142:
1139:
1134:
1131:
1128:
1124:
1120:
1117:
1114:
1111:
1101:
1062:
842:
841:Multiplication
839:
786:
785:
774:
771:
768:
748:
745:
742:
739:
736:
733:
730:
727:
724:
646:
645:
634:
631:
628:
625:
622:
619:
616:
613:
610:
607:
604:
590:
589:
578:
575:
572:
569:
566:
563:
560:
557:
554:
551:
548:
453:. In contrast
420:
417:
383:
382:
327:
326:
306:
303:
300:
297:
294:
289:
286:
283:
279:
275:
272:
269:
266:
256:
217:
79:
76:
56:exponentiation
52:multiplication
26:
24:
14:
13:
10:
9:
6:
4:
3:
2:
8055:
8044:
8041:
8039:
8036:
8035:
8033:
8024:
8021:
8020:
8016:
8010:
8006:
8002:
8001:
7996:
7992:
7989:
7988:0-444-86839-9
7985:
7982:. Elsevier.
7981:
7977:
7974:
7970:
7964:
7960:
7959:
7954:
7950:
7949:
7944:
7929:
7925:
7920:
7915:
7911:
7907:
7900:
7893:
7891:
7887:
7884:
7880:
7874:
7871:
7868:
7864:
7860:
7855:
7852:
7849:
7845:
7839:
7836:
7829:
7827:
7825:
7817:
7813:
7809:
7803:
7795:
7793:
7786:
7782:
7778:
7774:
7770:
7766:
7762:
7758:
7754:
7750:
7746:
7742:
7741:
7740:
7733:
7728:
7723:
7718:
7713:
7705:
7690:
7680:
7678:
7673:
7669:
7663:
7659:
7652:
7648:
7644:
7640:
7636:
7632:
7628:
7609:
7605:
7599:
7595:
7581:
7577:
7555:
7551:
7545:
7542:
7538:
7533:
7528:
7524:
7502:
7498:
7484:
7480:
7444:
7438:
7435:
7429:
7423:
7400:
7394:
7391:
7385:
7379:
7356:
7350:
7327:
7321:
7313:
7309:
7293:
7273:
7265:
7260:
7258:
7254:
7250:
7245:
7231:
7228:
7225:
7205:
7202:
7199:
7196:
7193:
7190:
7185:
7182:
7179:
7154:
7151:
7148:
7128:
7125:
7122:
7119:
7116:
7113:
7110:
7105:
7102:
7099:
7085:
7067:
7063:
7058:
7054:
7051:
7048:
7045:
7021:
7017:
7012:
7008:
7005:
6981:
6977:
6972:
6968:
6965:
6943:
6939:
6935:
6932:
6929:
6926:
6904:
6900:
6896:
6893:
6871:
6867:
6863:
6860:
6840:
6837:
6834:
6831:
6828:
6825:
6805:
6802:
6799:
6796:
6793:
6790:
6787:
6778:
6764:
6761:
6758:
6755:
6750:
6744:
6740:
6737:
6734:
6731:
6728:
6715:
6701:
6698:
6695:
6692:
6689:
6686:
6683:
6663:
6660:
6657:
6637:
6634:
6631:
6611:
6608:
6605:
6602:
6599:
6596:
6593:
6573:
6570:
6567:
6547:
6544:
6541:
6538:
6535:
6532:
6529:
6509:
6506:
6503:
6494:
6478:
6475:
6470:
6466:
6461:
6457:
6452:
6449:
6444:
6440:
6435:
6431:
6428:
6425:
6403:
6399:
6395:
6390:
6387:
6384:
6380:
6376:
6371:
6368:
6363:
6359:
6354:
6350:
6345:
6342:
6337:
6333:
6328:
6324:
6321:
6318:
6315:
6293:
6289:
6285:
6280:
6276:
6272:
6265:
6261:
6256:
6252:
6249:
6246:
6243:
6223:
6220:
6215:
6211:
6207:
6202:
6198:
6194:
6187:
6183:
6178:
6174:
6171:
6168:
6165:
6143:
6139:
6135:
6130:
6126:
6122:
6119:
6099:
6096:
6089:
6085:
6080:
6076:
6073:
6053:
6046:
6042:
6038:
6033:
6029:
6024:
6015:
6012:
6009:
6006:
6003:
5995:
5992:
5989:
5986:
5983:
5975:
5971:
5968:
5965:
5962:
5942:
5922:
5902:
5895:
5892:
5889:
5885:
5880:
5876:
5873:
5870:
5863:
5859:
5854:
5850:
5847:
5844:
5841:
5821:
5818:
5815:
5793:
5789:
5785:
5782:
5779:
5774:
5770:
5766:
5761:
5757:
5753:
5750:
5747:
5742:
5738:
5715:
5712:
5709:
5705:
5701:
5698:
5695:
5690:
5686:
5663:
5659:
5655:
5652:
5649:
5644:
5640:
5617:
5613:
5609:
5606:
5603:
5598:
5594:
5569:
5565:
5560:
5556:
5553:
5550:
5543:
5539:
5534:
5530:
5527:
5503:
5499:
5494:
5490:
5487:
5484:
5477:
5473:
5468:
5464:
5461:
5452:
5449:
5445:
5439:
5435:
5429:
5425:
5419:
5415:
5402:
5398:
5394:
5390:
5386:
5378:
5376:
5374:
5369:
5367:
5363:
5355:
5338:
5334:
5333:
5316:
5309:
5305:
5298:
5292:
5288:
5283:
5279:
5275:
5274:
5273:
5269:
5265:
5253:
5249:
5243:
5239:
5235:
5230:
5226:
5222:
5218:
5213:
5212:
5211:
5203:
5199:
5192:
5185:
5181:
5178:
5171:
5168:
5164:
5163:
5162:
5147:
5143:
5139:
5136:
5132:
5126:
5123:
5119:
5116:
5112:
5103:
5093:then writing
5091:
5087:
5082:
5066:
5061:
5060:
5059:
5053:
5050:
5049:
5048:
5045:
5041:
5037:
5031:
5027:
5023:
5019:
5012:
5008:
4994:
4993:gamma numbers
4988:
4981:
4976:
4973:
4972:delta numbers
4964:
4959:
4956:
4955:
4954:
4950:
4943:
4937:
4930:
4923:
4916:
4906:
4904:
4899:
4892:
4890:
4874:
4870:
4847:
4843:
4820:
4816:
4793:
4789:
4779:
4758:
4752:
4748:
4740:
4736:
4731:
4727:
4724:
4721:
4716:
4712:
4704:
4700:
4695:
4691:
4688:
4683:
4679:
4671:
4667:
4662:
4658:
4655:
4652:
4645:
4644:
4643:
4622:
4619:
4615:
4610:
4606:
4601:
4597:
4591:
4588:
4583:
4579:
4572:
4571:
4570:
4555:
4552:
4548:
4545:
4523:
4519:
4511:
4507:
4502:
4498:
4495:
4492:
4487:
4483:
4475:
4471:
4466:
4462:
4459:
4456:
4453:
4433:
4430:
4426:
4423:
4398:
4395:
4391:
4388:
4380:
4376:
4355:
4352:
4348:
4345:
4324:
4321:
4317:
4314:
4290:
4285:
4282:
4275:
4272:
4267:
4263:
4259:
4256:
4249:
4246:
4241:
4237:
4234:
4229:
4225:
4217:
4216:
4215:
4213:
4209:
4204:
4194:
4191:
4187:
4180:The ordinal ε
4164:
4160:
4156:
4149:
4145:
4140:
4135:
4130:
4126:
4121:
4116:
4112:
4108:
4105:
4101:
4096:
4092:
4088:
4085:
4081:
4078:
4071:
4070:
4069:
4051:
4047:
4042:
4038:
4033:
4029:
4016:
4012:
4005:
4001:
3997:
3990:The ordinal ε
3988:
3971:
3968:
3965:
3962:
3955:
3951:
3946:
3942:
3939:
3936:
3931:
3928:
3923:
3919:
3915:
3912:
3909:
3904:
3901:
3898:
3895:
3892:
3889:
3884:
3880:
3875:
3870:
3862:
3861:
3860:
3840:
3836:
3813:
3809:
3788:
3785:
3780:
3776:
3755:
3742:
3734:
3730:
3723:
3709:
3695:
3692:
3687:
3683:
3679:
3676:
3673:
3668:
3664:
3660:
3655:
3651:
3622:
3618:
3613:
3609:
3606:
3603:
3596:
3592:
3587:
3583:
3576:
3572:
3567:
3556:
3552:
3546:
3530:
3526:
3522:
3519:
3499:
3496:
3491:
3487:
3466:
3463:
3458:
3454:
3433:
3411:
3407:
3398:
3387:
3369:
3362:
3345:
3342:
3337:
3333:
3329:
3326:
3323:
3318:
3314:
3310:
3305:
3301:
3278:
3274:
3270:
3267:
3264:
3259:
3255:
3251:
3246:
3242:
3215:
3211:
3203:
3199:
3194:
3190:
3187:
3184:
3179:
3175:
3167:
3163:
3158:
3154:
3149:
3145:
3137:
3133:
3128:
3111:
3109:
3107:
3103:
3099:
3095:
3087:
3085:
3079:
3067:
3063:
3052:
3045:
3039:
3035:
3031:are given by
3029:
3025:
3019:
3015:
3010:
3002:
2998:
2992:
2988:
2981:
2977:
2973:
2969:
2950:
2943:
2930:
2925:
2918:
2912:
2908:
2902:
2898:
2891:
2886:
2882:
2875:
2871:
2865:
2861:
2856:
2852:
2848:
2842:
2838:
2831:
2826:
2821:
2817:
2813:
2809:
2805:
2798:
2794:
2790:
2786:
2768:
2764:
2760:
2755:
2751:
2747:
2743:
2739:
2735:
2731:
2727:
2721:
2713:
2707:
2702:
2698:
2697:
2693:
2691:
2675:
2657:
2653:
2647:
2641:
2637:
2632:
2627:
2622:
2617:
2610:
2606:
2599:
2595:
2588:
2584:
2578:
2574:
2570:
2559:
2555:
2548:
2541:
2537:
2530:
2519:
2515:
2506:
2483:
2479:
2471:
2467:
2462:
2458:
2455:
2452:
2447:
2443:
2435:
2431:
2426:
2422:
2417:
2413:
2405:
2401:
2396:
2386:
2380:
2374:
2370:
2366:
2359:
2352:
2348:
2339:
2332:
2328:
2319:
2296:
2292:
2284:
2280:
2275:
2271:
2268:
2265:
2260:
2256:
2248:
2244:
2239:
2235:
2230:
2226:
2218:
2214:
2209:
2199:
2193:
2187:
2182:
2181:binary number
2177:
2166:
2160:
2157:
2151:
2147:
2143:
2139:
2125:
2091:
2087:
2078:
2075:
2072:
2069:
2066:
2062:
2058:
2053:
2049:
2041:
2036:
2032:
2026:
2022:
2018:
2014:
2009:
2005:
2004:
2003:
2000:
1996:
1990:
1986:
1980:
1973:
1962:
1955:
1945:
1942:
1938:
1932:
1928:
1921:
1917:
1913:
1909:
1902:
1898:
1894:
1890:
1884:
1880:
1874:
1870:
1865:
1861:
1856:
1852:
1845:
1841:
1835:
1831:
1827:
1821:
1816:
1812:
1804:
1802:
1799:
1795:
1789:
1785:
1778:
1774:
1765:
1762:-number (see
1756:
1754:
1750:
1746:
1742:
1741:near-semiring
1737:
1734:
1730:
1726:
1722:
1718:
1708:
1704:
1698:
1694:
1690:
1686:
1671:
1658:
1654:
1653:left division
1649:
1645:
1641:
1634:
1630:
1624:
1620:
1616:
1612:
1605:
1600:
1595:
1591:
1587:
1583:
1576:
1572:
1568:
1562:
1557:
1553:
1549:
1545:
1541:
1534:
1530:
1526:
1522:
1518:
1513:
1509:
1490:
1486:
1472:
1469:
1465:
1461:
1457:
1451:
1447:
1441:
1437:
1433:
1427:
1422:
1418:
1414:
1410:
1403:
1397:
1393:
1386:
1382:
1378:
1374:
1370:
1366:
1359:
1355:
1351:
1344:
1337:
1333:
1329:
1324:
1318:
1314:
1306:
1304:
1301:
1298:
1294:
1290:
1286:
1282:
1237:
1236:
1235:
1232:
1225:
1221:
1180:
1179:
1178:
1174:
1146:
1143:
1140:
1132:
1129:
1126:
1122:
1118:
1115:
1112:
1109:
1102:
1097:
1093:
1087:
1083:
1079:
1075:
1071:
1067:
1063:
1057:
1056:
1055:
1052:
1048:
1042:
1038:
1034:
1027:
1023:
1016:
1005:
998:
988:
970:
957:
953:
948:
935:
927:
923:
917:
909:
900:
887:
879:
875:
871:
863:
859:
855:
847:
840:
838:
835:
830:
827:-number (see
813:
810:
806:
796:
792:
772:
769:
766:
746:
743:
740:
737:
734:
731:
728:
725:
722:
715:
714:
713:
710:
706:
702:
692:
688:
684:for ordinals
683:
678:
674:
668:
664:
660:
656:
651:
632:
629:
626:
623:
620:
617:
614:
608:
605:
602:
595:
594:
593:
576:
573:
570:
567:
564:
561:
558:
552:
549:
546:
539:
538:
537:
535:
531:
526:
523:
519:
515:
511:
507:
503:
497:
492:
490:
484:
457:
443:
436:
432:
426:
418:
416:
405:
401:
378:
377:
376:
373:
369:
359:
355:
348:
341:
332:
324:
323:limit ordinal
301:
298:
295:
287:
284:
281:
277:
273:
270:
267:
264:
257:
254:
253:
242:
238:
234:
230:
226:
222:
218:
215:
211:
207:
206:
205:
202:
198:
184:
180:
173:
163:
159:
152:
143:
138:
134:
128:
108:
101:
97:
93:
77:
75:
73:
69:
65:
61:
57:
53:
49:
45:
41:
37:
33:
19:
7999:
7979:
7957:
7931:. Retrieved
7909:
7905:
7873:
7863:Indag. Math.
7854:
7838:
7823:
7805:
7791:
7784:
7780:
7776:
7772:
7768:
7764:
7760:
7756:
7752:
7748:
7744:
7731:
7721:
7714:
7703:
7688:
7681:
7671:
7667:
7661:
7657:
7650:
7646:
7642:
7638:
7634:
7630:
7626:
7607:
7603:
7597:
7593:
7579:
7575:
7553:
7549:
7546:
7540:
7536:
7526:
7522:
7500:
7496:
7482:
7478:
7261:
7246:
7086:
6779:
6716:
6495:
5453:
5447:
5443:
5437:
5433:
5427:
5423:
5417:
5413:
5396:
5388:
5384:
5382:
5370:
5353:
5337:arithmetical
5336:
5330:
5320:
5307:
5303:
5296:
5290:
5286:
5281:
5277:
5267:
5263:
5260:
5251:
5247:
5241:
5237:
5233:
5228:
5224:
5220:
5216:
5209:
5201:
5197:
5196:> ⋯ >
5190:
5183:
5179:
5176:
5169:
5166:
5160:
5145:
5141:
5137:
5134:
5130:
5124:
5121:
5117:
5114:
5110:
5089:
5085:
5064:
5057:
5043:
5039:
5035:
5029:
5025:
5021:
5017:
5010:
5006:
4998:
4986:
4979:
4962:
4948:
4941:
4935:
4928:
4921:
4914:
4907:
4896:
4780:
4773:
4641:
4305:
4205:
4179:
4014:
4010:
4003:
3999:
3989:
3986:
3743:
3732:
3728:
3721:
3710:
3554:
3550:
3547:
3385:
3367:
3365:occurs when
3360:
3115:
3091:
3080:larger than
3065:
3061:
3050:
3043:
3037:
3033:
3027:
3023:
3017:
3013:
3007:
3000:
2996:
2990:
2986:
2979:
2975:
2971:
2967:
2948:
2941:
2923:
2916:
2910:
2906:
2900:
2896:
2889:
2880:
2873:
2869:
2863:
2859:
2850:
2846:
2840:
2836:
2829:
2819:
2815:
2811:
2807:
2803:
2796:
2792:
2788:
2784:
2762:
2758:
2749:
2745:
2741:
2733:
2729:
2711:
2700:
2655:
2651:
2645:
2639:
2635:
2630:
2625:
2618:
2608:
2604:
2597:
2593:
2586:
2582:
2580:which sends
2576:
2572:
2568:
2557:
2553:
2546:
2539:
2535:
2528:
2517:
2513:
2504:
2384:
2378:
2375:
2368:
2364:
2357:
2350:
2346:
2337:
2330:
2326:
2317:
2197:
2191:
2185:
2175:
2164:
2161:
2155:
2149:
2145:
2141:
2137:
2123:
2116:
2034:
2030:
2024:
2020:
2016:
2007:
1998:
1994:
1988:
1984:
1978:
1971:
1960:
1953:
1946:
1940:
1936:
1930:
1926:
1919:
1915:
1911:
1907:
1900:
1896:
1892:
1888:
1882:
1878:
1872:
1868:
1854:
1850:
1843:
1839:
1833:
1829:
1825:
1819:
1808:
1797:
1793:
1787:
1783:
1776:
1772:
1757:
1744:
1738:
1732:
1728:
1724:
1720:
1716:
1706:
1702:
1696:
1692:
1688:
1684:
1669:
1647:
1643:
1639:
1632:
1628:
1622:
1618:
1614:
1610:
1603:
1593:
1589:
1585:
1581:
1574:
1570:
1566:
1560:
1555:
1551:
1547:
1543:
1539:
1532:
1528:
1524:
1520:
1516:
1510:
1488:
1484:
1473:
1467:
1463:
1459:
1455:
1449:
1445:
1439:
1435:
1431:
1425:
1420:
1416:
1412:
1408:
1401:
1395:
1391:
1384:
1380:
1376:
1372:
1368:
1364:
1357:
1353:
1349:
1342:
1335:
1331:
1327:
1316:
1312:
1310:
1302:
1296:
1292:
1288:
1284:
1280:
1273:
1230:
1223:
1219:
1216:
1172:
1169:
1095:
1091:
1085:
1081:
1077:
1073:
1069:
1065:
1050:
1046:
1040:
1036:
1032:
1025:
1021:
1014:
1003:
996:
989:
955:
951:
944:
933:
925:
921:
915:
907:
885:
877:
873:
869:
861:
857:
853:
833:
814:
808:
804:
794:
790:
787:
708:
704:
700:
690:
686:
676:
672:
666:
662:
658:
654:
647:
591:
528:Addition is
527:
521:
517:
513:
509:
505:
501:
493:
482:
455:
441:
434:
430:
422:
403:
399:
384:
371:
367:
357:
353:
346:
339:
328:
250:
249:denotes the
240:
236:
232:
228:
224:
220:
213:
209:
200:
196:
182:
178:
171:
161:
157:
150:
136:
132:
129:
106:
99:
81:
39:
32:mathematical
29:
7953:Thomas Jech
7249:John Conway
5385:natural sum
5261:where each
4190:first-order
3104:. See also
872:,1) :
856:,0) :
496:associative
425:commutative
389:because in
375:looks like
8038:Set theory
8032:Categories
7945:References
7933:2024-08-28
7919:1501.05747
7623:such that
7218:, and not
7141:, and not
6958:. If both
6853:. If both
6418:, whereas
6236:, whereas
4013:when 0<
3009:Jacobsthal
2983:such that
2965:such that
2781:for which
2769:There are
2694:Properties
2633:functions
2607:= 1, ...,
2131:copies of
1837:such that
1714:such that
1682:such that
1565:(1 + 1) ·
1352:· 1 = 1 ·
1321:, and the
1315:· 0 = 0 ·
1307:Properties
802:such that
698:such that
534:continuous
489:equipotent
476:does not (
419:Properties
36:set theory
7701:and 2 is
7686:and 1 is
7436:⊗
7392:⊕
7310:(maximum
7232:ω
7229:⊗
7226:α
7206:ω
7203:α
7194:⊗
7191:α
7186:ω
7155:ω
7152:⊕
7149:α
7129:ω
7123:α
7114:⊕
7111:α
7106:ω
7068:γ
7064:ω
7059:ω
7052:β
7049:⊗
7046:α
7022:γ
7018:ω
7013:ω
7006:β
6982:γ
6978:ω
6973:ω
6966:α
6944:γ
6940:ω
6933:β
6930:⊕
6927:α
6905:γ
6901:ω
6894:β
6872:γ
6868:ω
6861:α
6841:β
6838:⊗
6835:α
6832:≤
6829:β
6826:α
6806:β
6803:⊕
6800:α
6797:≤
6794:β
6788:α
6762:⊗
6759:α
6745:⏟
6741:α
6738:⊕
6735:⋯
6732:⊕
6729:α
6702:γ
6699:⊗
6696:β
6690:γ
6687:⊗
6684:α
6658:γ
6638:β
6632:α
6624:; and if
6612:γ
6609:⊗
6606:β
6603:≤
6600:γ
6597:⊗
6594:α
6574:β
6571:≤
6568:α
6548:γ
6545:⊕
6542:β
6536:γ
6533:⊕
6530:α
6510:β
6504:α
6471:ω
6467:ω
6462:ω
6453:ω
6445:ω
6441:ω
6436:ω
6429:β
6426:α
6400:ω
6385:ω
6381:ω
6364:ω
6360:ω
6355:ω
6346:ω
6338:ω
6334:ω
6329:ω
6322:β
6319:⊗
6316:α
6290:ω
6281:ω
6277:ω
6266:ω
6262:ω
6257:ω
6250:β
6244:α
6224:ω
6212:ω
6203:ω
6199:ω
6188:ω
6184:ω
6179:ω
6172:β
6169:⊕
6166:α
6140:ω
6131:ω
6127:ω
6120:β
6100:ω
6090:ω
6086:ω
6081:ω
6074:α
6043:β
6039:⊕
6030:α
6025:ω
6016:ℓ
6013:≤
6007:≤
5993:≤
5987:≤
5976:⨁
5969:β
5966:⊗
5963:α
5943:β
5923:α
5896:ℓ
5886:γ
5881:ω
5874:⋯
5860:γ
5855:ω
5848:β
5845:⊕
5842:α
5822:β
5819:⊕
5816:α
5794:ℓ
5790:β
5783:…
5771:β
5758:α
5751:…
5739:α
5716:ℓ
5706:γ
5699:…
5687:γ
5664:ℓ
5660:β
5656:≥
5653:⋯
5650:≥
5641:β
5614:α
5610:≥
5607:⋯
5604:≥
5595:α
5570:ℓ
5566:β
5561:ω
5554:⋯
5540:β
5535:ω
5528:β
5500:α
5495:ω
5488:⋯
5474:α
5469:ω
5462:α
5001:2×3 = 3×2
4844:β
4790:β
4737:β
4732:ω
4725:⋯
4701:β
4696:ω
4668:β
4663:ω
4653:α
4620:β
4607:β
4602:ω
4589:β
4584:ω
4580:α
4553:β
4508:β
4503:ω
4496:⋯
4472:β
4467:ω
4460:α
4434:β
4424:β
4415:, and if
4381:β
4377:ω
4356:β
4346:β
4325:β
4315:β
4273:β
4268:ω
4247:β
4242:ω
4230:β
4226:ω
4203:itself).
4161:…
4150:ω
4146:ω
4141:ω
4131:ω
4127:ω
4113:ω
4106:ω
4093:ω
4048:ε
4043:ω
4030:ε
3963:⋅
3956:ω
3952:ω
3947:ω
3937:⋅
3920:ω
3910:⋅
3899:ω
3890:⋅
3881:ω
3876:ω
3871:ω
3837:β
3810:β
3789:α
3777:β
3756:ω
3693:≥
3684:β
3680:≥
3677:…
3674:≥
3665:β
3661:≥
3652:β
3619:β
3614:ω
3607:⋯
3593:β
3588:ω
3573:β
3568:ω
3531:α
3527:ω
3520:α
3500:α
3488:β
3467:α
3464:≤
3455:β
3434:α
3408:β
3343:≥
3334:β
3327:…
3315:β
3302:β
3268:…
3200:β
3195:ω
3188:⋯
3164:β
3159:ω
3134:β
3129:ω
3098:pentation
3094:tetration
2672:ℵ
2463:α
2456:⋯
2427:α
2397:α
2276:ω
2269:⋯
2240:ω
2210:ω
2092:δ
2088:α
2079:β
2073:δ
2063:⋃
2054:β
2050:α
1780:whenever
1743:, but do
1657:remainder
1601:law: If
1213:< ...,
1147:δ
1144:⋅
1141:α
1133:β
1127:δ
1123:⋃
1116:β
1113:⋅
1110:α
770:≠
747:ω
741:ω
729:ω
633:γ
627:β
624:≤
621:γ
615:α
612:⇒
609:β
603:α
577:β
571:γ
565:α
559:γ
556:⇒
553:β
547:α
302:δ
296:α
288:β
282:δ
278:⋃
271:β
265:α
255:function.
252:successor
34:field of
7997:(1958),
7978:, 1980.
7775:+ 1) = (
7655:for all
7591:for all
7573:for all
7494:; while
6717:We have
4623:′
4592:′
4556:′
4427:′
4399:′
4349:′
4318:′
4286:′
4276:′
4260:′
4250:′
3639:, where
3230:, where
3102:hexation
2931:For all
2879:2 = 3 =
2571: :
1992:for all
1965:for any
1929:∈
1924:for all
1881:∈
1853:∈
1828: :
1278:. Thus,
1270:< ...
1061:· 0 = 0.
1044:for all
1008:for any
920: :
902:The set
245:, where
194:for all
165:for any
78:Addition
70:and the
48:addition
8009:0095787
7808:nimbers
7763:+ 1 = (
7641:) <
7583:and of
6158:. Then
5678:). Let
4933:, ...,
4862:, then
4835:, then
4808:, then
4569:, then
4214:) that
4188:of the
3855:as for
3078:-number
2985:0 <
2904:, then
2867:, then
2844:, then
2806:· 2) =
2715:, then
2710:0 <
2552:, ...,
2511:, ...,
2344:, ...,
2324:, ...,
2135:; e.g.
2109:, when
1969:. For
1895:) <
1860:support
1782:0 <
1747:form a
1731:+ 1) ·
1626:, then
1325:holds:
1162:, when
1012:. For
1006:· 0 = 0
807:+ 42 =
670:, then
512:+ (4 +
504:+ 4) +
169:. For
30:In the
8007:
7986:
7965:
7802:Nimber
7783:+ 1) (
7767:+ 1) (
7633:) ⊕ (
7167:; and
6308:. And
5302:≥ ⋯ ≥
5289:+ ⋯ +
5188:(with
5175:+ ⋯ +
5068:where
4989:> 0
4015:α
4011:α
4004:β
4000:α
3724:> 1
3376:s nor
3100:, and
3073:is an
3069:where
2961:, and
2951:> 0
2944:> 1
2892:> 1
2832:> 1
2818:· 2 ≠
2777:, and
2616:to 0.
2544:, and
2498:where
2311:where
1974:> 0
1672:> 0
1642:= 2 ·
1606:> 0
1584:+ 1 ·
1578:while
1569:= 2 ·
1434:= 2 ·
1404:> 0
1334:= 0 →
1295:= 2 ·
1283:· 2 =
1266:< 1
1262:< 0
1258:< 1
1254:< 0
1250:< 1
1246:< 0
1242:< 1
1209:< 3
1205:< 2
1201:< 1
1193:< 3
1189:< 2
1185:< 1
1017:> 0
472:) and
212:+ 0 =
174:> 0
160:+ 0 =
54:, and
7914:arXiv
7902:(PDF)
7830:Notes
7670:<
7660:<
7596:<
7578:<
7476:; so
7308:types
7306:, of
7253:field
7038:then
6919:then
6676:then
6586:then
6560:; if
6522:then
5360:(the
5294:with
5108:. If
3972:65537
3055:, or
3041:, or
3021:with
2999:<
2989:<
2939:, if
2914:. If
2862:<
2849:<
2839:<
2814:·2 =
2723:1 = 1
2717:0 = 0
2526:with
1997:<
1939:<
1934:with
1886:with
1871:<
1846:) = 0
1786:<
1705:<
1667:, if
1655:with
1415:<
1394:<
1076:) = (
1049:<
652:: if
393:only
321:is a
317:when
199:<
109:× {1}
102:× {0}
7984:ISBN
7963:ISBN
7883:here
7867:here
7848:here
7787:+ 1)
7665:and
7615:and
7587:and
7569:and
7561:and
7516:and
7508:and
7490:and
7472:and
7464:and
7343:and
7286:and
7183:<
7103:<
7055:<
7009:<
6998:and
6969:<
6936:<
6897:<
6886:and
6864:<
6818:and
6693:<
6661:>
6650:and
6635:<
6539:<
6507:<
6112:and
5935:and
5632:and
5520:and
5407:and
5387:and
5383:The
5250:+ 1)
5236:+ 1)
5144:+ 1)
5033:and
5020:+1)×
4642:and
4549:<
4457:<
4431:<
4337:(if
4322:>
4210:and
4009:<
3913:1729
3786:<
3330:>
3324:>
3311:>
3048:and
2994:and
2946:and
2935:and
2926:= 0
2919:= 1
2894:and
2834:and
2791:) ≠
2761:) =
2602:for
2174:2 =
2076:<
2070:<
2023:) ·
1914:) =
1905:and
1749:ring
1700:and
1678:and
1663:and
1638:1 ·
1608:and
1580:1 ·
1527:) =
1496:and
1478:and
1430:1 ·
1406:) →
1399:and
1371:) ·
1229:2 ·
1130:<
1084:) +
1039:) +
983:and
963:and
945:The
932:2 •
759:but
606:<
568:<
550:<
532:and
516:) =
487:are
480:and
440:3 +
429:3 +
411:and
285:<
231:) =
190:and
104:and
86:and
7924:doi
7824:not
7820:mex
7706:· 2
7691:+ 1
7645:⊕ (
7255:of
7251:'s
7176:lim
7096:lim
5441:or
5421:or
5246:⋯ (
5133:= (
5083:If
4982:+ 1
4951:+ 1
4944:+ 1
4931:+ 1
4924:+ 1
4917:+ 1
4905:).
4774:if
4306:if
3388:of
3370:= 0
3363:= 0
3053:= 4
3046:= 2
2921:or
2887:If
2857:If
2822:· 4
2810:·2·
2708:If
2703:= 1
2631:all
2591:to
2019:= (
2010:= 1
1963:= 1
1956:= 0
1745:not
1727:≤ (
1561:not
1559:is
1426:not
1379:· (
1345:= 0
1340:or
1338:= 0
1319:= 0
1175:· 2
999:= 0
914:(1,
906:(0,
888:• 2
868:{ (
852:{ (
485:+ 3
458:+ 3
445:is
349:+ 2
342:+ 1
153:= 0
144:on
8034::
8005:MR
7922:.
7910:63
7908:.
7904:.
7889:^
7779:+
7771:+
7759:+
7755:+
7751:+
7747:+
7712:.
7649:⊗
7637:⊗
7629:⊗
7606:⊗
7552:⊕
7544:.
7539:⊗
7525:⊕
7499:⊗
7481:⊕
7314:)
7259:.
7244:.
7084:.
6777:.
6714:.
6493:.
5451:.
5446:⨳
5436:⊗
5426:#
5416:⊕
5368:.
5285:=
5244:−1
5219:⋯
5120:+
5113:=
5088:=
5065:αβ
5042:=
5024:=
5014:,
5009:=
5005:2×
5003:,
4946:,
4939:,
4926:,
4919:,
4912:,
3932:88
3905:42
3741:.
3108:.
3096:,
3084:.
3066:εα
3064:=
3036:=
3026:≤
3016:=
2978:+
2974:·
2970:=
2957:,
2909:=
2899:=
2872:≤
2795:·
2787:·
2773:,
2748:=
2732:=
2654:→
2638:→
2575:→
2373:.
2315:,
2140:=
1987:·
1832:→
1801:.
1796:=
1775:=
1773:αβ
1758:A
1736:.
1723:≤
1719:·
1695:+
1691:·
1687:=
1646:=
1631:=
1621:·
1617:=
1613:·
1592:+
1588:=
1573:=
1556:γα
1552:βα
1550:=
1542:+
1533:αγ
1531:+
1529:αβ
1523:+
1487:=
1471:.
1462:≤
1453:→
1448:≤
1438:=
1383:·
1375:=
1367:·
1356:=
1330:·
1291:≠
1222:+
1177::
1080:·
1068:·
1035:·
1024:·
987:.
954:×
949:,
928:}
924:∈
912:,
904:{
880:}
876:∈
866:∪
864:}
860:∈
837:.
812:.
793:≤
707:+
703:=
689:≤
675:=
665:+
661:=
657:+
525:.
520:+
508:=
470:2'
433:=
413:0'
402:+
370:+
356:+
344:,
239:+
223:+
181:+
135:+
127:.
74:.
50:,
46::
38:,
7990:.
7971:.
7936:.
7926::
7916::
7785:x
7781:x
7777:x
7773:x
7769:x
7765:x
7761:x
7757:x
7753:x
7749:x
7745:x
7737:x
7732:ω
7722:ω
7710:ω
7704:ω
7699:ω
7695:ω
7689:ω
7684:ω
7672:β
7668:δ
7662:α
7658:ε
7653:)
7651:δ
7647:ε
7643:γ
7639:β
7635:ε
7631:δ
7627:α
7625:(
7621:γ
7617:β
7613:α
7608:β
7604:α
7598:α
7594:γ
7589:β
7585:γ
7580:β
7576:γ
7571:γ
7567:α
7563:β
7559:α
7554:β
7550:α
7541:β
7537:α
7527:β
7523:α
7518:β
7514:α
7510:β
7506:α
7501:β
7497:α
7492:β
7488:α
7483:β
7479:α
7474:β
7470:α
7466:T
7462:S
7448:)
7445:T
7442:(
7439:o
7433:)
7430:S
7427:(
7424:o
7404:)
7401:T
7398:(
7395:o
7389:)
7386:S
7383:(
7380:o
7360:)
7357:T
7354:(
7351:o
7331:)
7328:S
7325:(
7322:o
7294:T
7274:S
7200:=
7197:n
7180:n
7126:+
7120:=
7117:n
7100:n
6791:+
6765:n
6756:=
6751:n
6664:0
6479:5
6476:+
6458:+
6450:+
6432:=
6404:6
6396:+
6391:1
6388:+
6377:+
6372:5
6369:+
6351:+
6343:+
6325:=
6294:5
6286:+
6273:+
6253:=
6247:+
6221:+
6216:5
6208:+
6195:+
6175:=
6144:5
6136:+
6123:=
6097:+
6077:=
6054:.
6047:j
6034:i
6010:j
6004:1
5996:k
5990:i
5984:1
5972:=
5903:.
5893:+
5890:k
5877:+
5871:+
5864:1
5851:=
5786:,
5780:,
5775:1
5767:,
5762:k
5754:,
5748:,
5743:1
5713:+
5710:k
5702:,
5696:,
5691:1
5645:1
5618:k
5599:1
5557:+
5551:+
5544:1
5531:=
5504:k
5491:+
5485:+
5478:1
5465:=
5448:β
5444:α
5438:β
5434:α
5428:β
5424:α
5418:β
5414:α
5409:β
5405:α
5357:1
5354:ω
5349:0
5345:0
5341:0
5327:ω
5323:0
5312:.
5308:m
5304:β
5300:1
5297:β
5291:ω
5287:ω
5282:k
5278:α
5268:i
5264:n
5255:1
5252:n
5248:ω
5242:k
5238:n
5234:ω
5232:(
5229:k
5225:n
5223:)
5221:ω
5217:ω
5215:(
5206:)
5202:k
5198:α
5194:1
5191:α
5184:k
5180:n
5177:ω
5173:1
5170:n
5167:ω
5157:.
5155:β
5151:m
5146:m
5142:ω
5138:n
5135:ω
5131:β
5125:n
5122:ω
5118:m
5115:ω
5111:β
5106:β
5099:α
5095:γ
5090:ω
5086:α
5078:β
5074:ω
5070:α
5044:ω
5040:ω
5038:×
5036:ω
5030:ω
5028:×
5026:ω
5022:ω
5018:ω
5016:(
5011:ω
5007:ω
4987:α
4980:ω
4968:α
4963:ω
4949:ω
4942:ω
4936:ω
4929:ω
4922:ω
4915:ω
4910:ω
4875:2
4871:c
4848:2
4821:1
4817:c
4794:1
4776:n
4759:,
4753:k
4749:c
4741:k
4728:+
4722:+
4717:2
4713:c
4705:2
4692:+
4689:n
4684:1
4680:c
4672:1
4659:=
4656:n
4616:+
4611:1
4598:=
4546:0
4524:k
4520:c
4512:k
4499:+
4493:+
4488:1
4484:c
4476:1
4463:=
4454:0
4403:)
4396:c
4392:+
4389:c
4386:(
4353:=
4291:,
4283:c
4264:=
4257:c
4238:+
4235:c
4201:0
4197:0
4182:0
4165:.
4157:,
4136:,
4122:,
4117:1
4109:=
4102:,
4097:0
4089:=
4086:1
4082:,
4079:0
4052:0
4039:=
4034:0
4019:ω
4007:1
3994:(
3992:0
3969:+
3966:5
3943:+
3940:3
3929:+
3924:9
3916:+
3902:+
3896:+
3893:6
3885:7
3857:α
3841:i
3814:i
3781:1
3746:α
3739:δ
3733:i
3729:c
3722:δ
3717:ω
3713:δ
3696:0
3688:k
3669:2
3656:1
3641:k
3623:k
3610:+
3604:+
3597:2
3584:+
3577:1
3555:i
3551:c
3523:=
3497:=
3492:1
3459:1
3412:1
3394:ω
3390:α
3382:α
3378:c
3374:β
3368:k
3361:α
3346:0
3338:k
3319:2
3306:1
3279:k
3275:c
3271:,
3265:,
3260:2
3256:c
3252:,
3247:1
3243:c
3232:k
3216:k
3212:c
3204:k
3191:+
3185:+
3180:2
3176:c
3168:2
3155:+
3150:1
3146:c
3138:1
3118:α
3082:α
3076:ε
3071:ε
3062:β
3057:α
3051:β
3044:α
3038:β
3034:α
3028:β
3024:α
3018:β
3014:α
3004:.
3001:β
2997:ρ
2991:β
2987:δ
2980:ρ
2976:δ
2972:β
2968:α
2963:ρ
2959:δ
2955:γ
2949:α
2942:β
2937:β
2933:α
2924:α
2917:α
2911:γ
2907:β
2901:α
2897:α
2890:α
2884:.
2881:ω
2874:β
2870:α
2864:β
2860:α
2854:.
2851:γ
2847:γ
2841:β
2837:α
2830:γ
2824:.
2820:ω
2816:ω
2812:ω
2808:ω
2804:ω
2802:(
2797:β
2793:α
2789:β
2785:α
2783:(
2779:γ
2775:β
2771:α
2766:.
2763:α
2759:α
2757:(
2753:.
2750:α
2746:α
2744:·
2742:α
2737:.
2734:α
2730:α
2725:.
2719:.
2712:α
2705:.
2701:α
2676:0
2661:ω
2656:α
2652:β
2646:α
2640:A
2636:B
2626:A
2614:β
2609:k
2605:i
2598:i
2594:a
2587:i
2583:b
2577:α
2573:β
2569:f
2564:α
2558:k
2554:a
2550:1
2547:a
2540:k
2536:b
2532:1
2529:b
2524:β
2518:k
2514:b
2508:1
2505:b
2500:k
2484:k
2480:a
2472:k
2468:b
2459:+
2453:+
2448:2
2444:a
2436:2
2432:b
2423:+
2418:1
2414:a
2406:1
2402:b
2385:α
2379:α
2369:k
2365:n
2361:1
2358:n
2351:k
2347:c
2341:1
2338:c
2331:k
2327:n
2321:1
2318:n
2313:k
2297:k
2293:c
2285:k
2281:n
2272:+
2266:+
2261:2
2257:c
2249:2
2245:n
2236:+
2231:1
2227:c
2219:1
2215:n
2198:ω
2192:ω
2186:ω
2176:ω
2170:α
2165:α
2156:ω
2150:ω
2148:·
2146:ω
2144:·
2142:ω
2138:ω
2133:α
2129:β
2124:α
2119:β
2111:β
2097:)
2084:(
2067:0
2059:=
2039:.
2037:)
2035:β
2033:(
2031:S
2025:α
2021:α
2017:α
2012:.
2008:α
1999:β
1995:δ
1989:α
1985:α
1979:α
1972:β
1967:α
1961:α
1954:β
1949:β
1941:y
1937:x
1931:β
1927:y
1922:)
1920:y
1918:(
1916:g
1912:y
1910:(
1908:f
1903:)
1901:x
1899:(
1897:g
1893:x
1891:(
1889:f
1883:β
1879:x
1873:g
1869:f
1855:β
1851:x
1844:x
1842:(
1840:f
1834:α
1830:β
1826:f
1820:α
1798:ω
1794:β
1788:β
1784:α
1777:β
1768:β
1760:δ
1733:ω
1729:α
1725:ω
1721:ω
1717:α
1712:α
1707:β
1703:δ
1697:δ
1693:γ
1689:β
1685:α
1680:δ
1676:γ
1670:β
1665:β
1661:α
1648:ω
1644:ω
1640:ω
1633:γ
1629:β
1623:γ
1619:α
1615:β
1611:α
1604:α
1594:ω
1590:ω
1586:ω
1582:ω
1575:ω
1571:ω
1567:ω
1554:+
1548:α
1546:)
1544:γ
1540:β
1538:(
1525:γ
1521:β
1519:(
1517:α
1506:β
1502:α
1498:n
1494:m
1489:β
1485:α
1480:β
1476:α
1468:γ
1466:·
1464:β
1460:γ
1458:·
1456:α
1450:β
1446:α
1440:ω
1436:ω
1432:ω
1421:β
1419:·
1417:γ
1413:α
1411:·
1409:γ
1402:γ
1396:β
1392:α
1387:)
1385:γ
1381:β
1377:α
1373:γ
1369:β
1365:α
1363:(
1358:α
1354:α
1350:α
1343:β
1336:α
1332:β
1328:α
1317:α
1313:α
1297:ω
1293:ω
1289:ω
1287:+
1285:ω
1281:ω
1276:ω
1268:3
1264:3
1260:2
1256:2
1252:1
1248:1
1244:0
1240:0
1238:0
1231:ω
1224:ω
1220:ω
1211:1
1207:1
1203:1
1199:1
1195:0
1191:0
1187:0
1183:0
1181:0
1173:ω
1164:β
1150:)
1138:(
1119:=
1100:.
1098:)
1096:β
1094:(
1092:S
1086:α
1082:β
1078:α
1074:β
1072:(
1070:S
1066:α
1059:α
1051:β
1047:δ
1041:α
1037:δ
1033:α
1031:(
1026:β
1022:α
1015:β
1010:α
1004:α
997:β
992:β
985:T
981:S
977:S
973:T
965:T
961:S
956:T
952:S
941:.
939:ω
934:ω
926:N
922:n
918:)
916:n
910:)
908:n
894:.
892:ω
886:ω
878:N
874:n
870:n
862:N
858:n
854:n
834:ω
825:γ
821:α
817:α
809:ω
805:γ
800:γ
795:α
791:β
773:0
767:3
744:=
738:+
735:0
732:=
726:+
723:3
709:γ
705:β
701:α
696:γ
691:α
687:β
677:γ
673:β
667:γ
663:α
659:β
655:α
630:+
618:+
574:+
562:+
522:ω
518:ω
514:ω
510:ω
506:ω
502:ω
500:(
483:ω
478:ω
474:ω
462:ω
456:ω
451:ω
442:ω
435:ω
431:ω
409:0
404:ω
400:ω
395:0
391:ω
387:ω
372:ω
368:ω
358:ω
354:ω
347:ω
340:ω
335:ω
325:.
319:β
305:)
299:+
293:(
274:=
268:+
247:S
243:)
241:β
237:α
235:(
233:S
229:β
227:(
225:S
221:α
214:α
210:α
201:β
197:δ
192:δ
188:α
183:β
179:α
172:β
167:α
162:α
158:α
151:β
146:β
137:β
133:α
125:T
121:S
117:T
113:S
107:T
100:S
88:T
84:S
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.