67:, even one without symmetries, by choosing any point interior to the polyhedron as its center. For these polyhedra, the density will be 1. More generally, for any non-self-intersecting (acoptic) polyhedron, the density can be computed as 1 by a similar calculation that chooses a ray from an interior point that only passes through facets of the polyhedron, adds one when this ray passes from the interior to the exterior of the polyhedron, and subtracts one when this ray passes from the exterior to the interior of the polyhedron. However, this assignment of signs to crossings does not generally apply to star polyhedra, as they do not have a well-defined interior and exterior.
762:
211:
403:
233:
143:
870:
159:
808:
377:
174:
620:
355:
196:
613:
20:
59:
of the polytope and not through any lower dimensional features, and counting how many facets it passes through. For polyhedra for which this count does not depend on the choice of the ray, and for which the central point is not itself on any facet, the density is given by this count of crossed
761:
645:
generalized the formula for star polyhedra with different kinds of face, some of which may fold backwards over others. The resulting value for density corresponds to the number of times the associated spherical polyhedron covers the sphere.
747:
601:
The regular star polyhedra exist in two dual pairs, with each figure having the same density as its dual: one pair (small stellated dodecahedron—great dodecahedron) has a density of 3, while the other (
402:
807:
376:
232:
142:
539:
210:
173:
354:
889:), which have densities between 4, 6, 20, 66, 76, and 191. They come in dual pairs, with the exception of the self-dual density-6 and density-66 figures.
158:
1051:
985:
922:
651:
937:
17. The angle defect of a polyhedron; 20. Curvature of surfaces; 21. Gaussian curvature; 27.3.1 Curvature for
Polyhedra pp. 32-51
991:
874:
48:
602:
579:
131:. It can be visually determined by counting the minimum number of edge crossings of a ray from the center to infinity.
195:
85:
is the number of times that the polygonal boundary winds around its center. For convex polygons, and more generally
869:
452:
976:
55:
of the polyhedron. It can be determined by passing a ray from the center to infinity, passing only through the
631:, {3,5/2} has a density of 7 as demonstrated in this transparent and cross-sectional view on the right.
483:
996:
Philosophical
Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences
308:
149:
90:
24:
413:
387:
383:
312:
1095:
1019:
886:
814:
583:
436:
277:
269:
104:
of all the vertices divided by 360°. This will be an integer for all unicursal paths in a plane.
52:
1068:
1047:
1043:
1011:
981:
918:
910:
752:
628:
545:
64:
1003:
619:
291:, leaving an angle defect of π/2. 8×π/2=4π. So the density of the cube is 1.
164:
56:
1031:
1027:
768:
257:
216:
179:
40:
107:
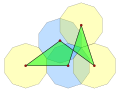
The density of a compound polygon is the sum of the densities of the component polygons.
300:
97:
86:
73:
can similarly define density as the number of coverings of faces over any given point.
70:
44:
1089:
858:
854:
578:
This implies a density of 7. The unmodified Euler's polyhedron formula fails for the
463:
428:
304:
1071:
1038:
Wenninger, Magnus J. (1979), "An introduction to the notion of polyhedral density",
273:
182:
116:
947:
642:
612:
857:, some of whose faces pass through the center, the density cannot be defined.
19:
882:
751:
This allowed
Coxeter et al. to determine the densities of the majority of the
239:
101:
1015:
1076:
556:
201:
1007:
219:
32:
994:; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra",
1023:
288:
47:
from two dimensions to higher dimensions, representing the number of
914:
934:
868:
18:
961:
Coxeter, 1954 (Section 6, Density and Table 7, Uniform polyhedra)
365:
284:
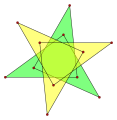
27:{9/4} winds around its centre 4 times, so it has a density of 4.
742:{\displaystyle \sum _{i}d_{vi}v_{i}-e+\sum _{i}d_{fi}f_{i}=2D}
16:
Number of windings of a polytope around its center of symmetry
925:(206–214, Density of regular honeycombs in hyperbolic space)
775:, {8/2}×{}, shown here with offset vertices for clarity.
755:, which have one vertex type, and multiple face types.
654:
486:
607:
861:polyhedra also do not have well-defined densities.
280:(summed over all its vertices) divided by 4π.
741:
533:
89:(not self-intersecting), the density is 1, by the
96:The density of a polygon can also be called its
272:concentrated at the vertices and defined by an
276:. The density of a polyhedron is equal to the
268:A polyhedron can be considered a surface with
63:The same calculation can be performed for any
8:
360:Density of topological sphere polyhedron is
246:}, has density 5, similar to regular {12/5}.
935:Geometry and the Imagination in Minneapolis
189:}, has density 2, similar to regular {7/2}.
548:, {3, 5/2}, has 20 triangular faces (
952:, CUP hbk (1997), pbk. (1999). (Page 258)
724:
711:
701:
682:
669:
659:
653:
513:
491:
485:
605:–great icosahedron) has a density of 7.
898:
757:
350:
138:
980:, (3rd edition, 1973), Dover edition,
43:is a generalization of the concept of
907:The Beauty of Geometry: Twelve Essays
148:A single-crossing polygon, like this
7:
71:Tessellations with overlapping faces
534:{\displaystyle d_{v}v-e+d_{f}f=2D}
14:
555: = 1), 30 edges and 12
408:Density of a genus 5 toroidal is
299:The density of a polyhedron with
806:
760:
618:
611:
401:
375:
353:
231:
209:
194:
172:
157:
141:
570:2·12 − 30 + 1·20 = 14 = 2
875:great grand stellated 120-cell
477:of the polyhedron as a whole:
1:
51:of the polyhedron around the
909:(1999), Dover Publications,
603:great stellated dodecahedron
580:small stellated dodecahedron
287:has 8 vertices, each with 3
23:The boundary of the regular
582:{5/2, 5} and its dual
435:as a way to modify Euler's
394:, like this hexagonal form:
1112:
881:There are 10 regular star
887:Schläfli–Hess 4-polytopes
626:
586:{5, 5/2}, for which
1042:, CUP Archive, pp.
566: = 2), giving
849:Nonorientable polyhedra
260:have the same density.
1008:10.1098/rsta.1954.0003
878:
743:
638:General star polyhedra
535:
453:regular star polyhedra
424:Regular star polyhedra
28:
872:
744:
536:
451:= 2) to work for the
256:A polyhedron and its
111:Regular star polygons
22:
652:
484:
462:is the density of a
309:Euler Characteristic
204:{7/3} has density 3.
150:equilateral pentagon
91:Jordan curve theorem
83:density of a polygon
974:Coxeter, H. S. M.;
865:Regular 4-polytopes
771:, wrapped twice is
388:toroidal polyhedron
319:, its density is 1-
1069:Weisstein, Eric W.
905:Coxeter, H. S. M;
879:
815:pentagrammic prism
767:The density of an
739:
706:
664:
584:great dodecahedron
531:
437:polyhedron formula
418:v=72, e=168, f=88.
270:Gaussian curvature
222:(compound) 2{(3/2)
167:{5} has density 1.
127:}, the density is
53:center of symmetry
29:
1072:"Polygon density"
1053:978-0-521-22279-2
992:Coxeter, H. S. M.
977:Regular Polytopes
813:The density of a
753:uniform polyhedra
697:
655:
635:
634:
629:great icosahedron
546:great icosahedron
544:For example, the
396:v=24, e=48, f=24.
311:, χ. If its
100:; the sum of the
65:convex polyhedron
1103:
1082:
1081:
1056:
1040:Spherical models
1034:
1002:(916): 401–450,
962:
959:
953:
944:
938:
932:
926:
903:
877:has density 191.
810:
764:
748:
746:
745:
740:
729:
728:
719:
718:
705:
687:
686:
677:
676:
663:
622:
615:
608:
559:vertex figures (
540:
538:
537:
532:
518:
517:
496:
495:
405:
379:
357:
295:Simple polyhedra
235:
226:} has density 4.
213:
198:
176:
165:Regular pentagon
161:
152:, has density 0.
145:
1111:
1110:
1106:
1105:
1104:
1102:
1101:
1100:
1086:
1085:
1067:
1066:
1063:
1054:
1037:
990:
971:
966:
965:
960:
956:
945:
941:
933:
929:
904:
900:
895:
867:
851:
844:
842:
838:
834:
832:
828:
824:
822:
811:
802:
800:
796:
792:
788:
786:
782:
778:
776:
769:octagonal prism
765:
720:
707:
678:
665:
650:
649:
640:
565:
554:
509:
487:
482:
481:
472:
461:
426:
419:
417:
406:
397:
395:
380:
371:
370:v=8, e=12, f=6.
369:
358:
307:is half of the
297:
283:For example, a
278:total curvature
266:
264:Total curvature
254:
247:
245:
236:
227:
225:
214:
205:
199:
190:
188:
177:
168:
162:
153:
146:
137:
113:
87:simple polygons
79:
41:star polyhedron
17:
12:
11:
5:
1109:
1107:
1099:
1098:
1088:
1087:
1084:
1083:
1062:
1061:External links
1059:
1058:
1057:
1052:
1035:
988:
970:
967:
964:
963:
954:
946:Cromwell, P.;
939:
927:
897:
896:
894:
891:
866:
863:
859:Non-orientable
850:
847:
846:
845:
840:
836:
830:
826:
817:, {5/2}×{} is
812:
805:
803:
798:
794:
790:
784:
780:
766:
759:
738:
735:
732:
727:
723:
717:
714:
710:
704:
700:
696:
693:
690:
685:
681:
675:
672:
668:
662:
658:
639:
636:
633:
632:
627:The nonconvex
624:
623:
616:
576:
575:
563:
552:
542:
541:
530:
527:
524:
521:
516:
512:
508:
505:
502:
499:
494:
490:
473:of a face and
470:
459:
425:
422:
421:
420:
414:Stewart_toroid
407:
400:
398:
381:
374:
372:
359:
352:
349:
348:
305:vertex figures
296:
293:
265:
262:
253:
250:
249:
248:
243:
237:
230:
228:
223:
215:
208:
206:
200:
193:
191:
186:
178:
171:
169:
163:
156:
154:
147:
140:
136:
133:
115:For a regular
112:
109:
98:turning number
78:
75:
45:winding number
15:
13:
10:
9:
6:
4:
3:
2:
1108:
1097:
1094:
1093:
1091:
1079:
1078:
1073:
1070:
1065:
1064:
1060:
1055:
1049:
1045:
1041:
1036:
1033:
1029:
1025:
1021:
1017:
1013:
1009:
1005:
1001:
997:
993:
989:
987:
986:0-486-61480-8
983:
979:
978:
973:
972:
968:
958:
955:
951:
950:
943:
940:
936:
931:
928:
924:
923:0-486-40919-8
920:
916:
912:
908:
902:
899:
892:
890:
888:
884:
876:
871:
864:
862:
860:
856:
855:hemipolyhedra
848:
820:
816:
809:
804:
774:
770:
763:
758:
756:
754:
749:
736:
733:
730:
725:
721:
715:
712:
708:
702:
698:
694:
691:
688:
683:
679:
673:
670:
666:
660:
656:
647:
644:
637:
630:
625:
621:
617:
614:
610:
609:
606:
604:
599:
597:
593:
589:
585:
581:
573:
569:
568:
567:
562:
558:
551:
547:
528:
525:
522:
519:
514:
510:
506:
503:
500:
497:
492:
488:
480:
479:
478:
476:
469:
465:
464:vertex figure
458:
454:
450:
446:
442:
438:
434:
430:
429:Arthur Cayley
423:
415:
411:
404:
399:
393:
389:
385:
382:Density of a
378:
373:
367:
363:
356:
351:
346:
342:
338:
334:
330:
326:
325:
324:
322:
318:
314:
310:
306:
302:
294:
292:
290:
286:
281:
279:
275:
271:
263:
261:
259:
251:
241:
234:
229:
221:
218:
212:
207:
203:
197:
192:
184:
181:
175:
170:
166:
160:
155:
151:
144:
139:
134:
132:
130:
126:
122:
118:
110:
108:
105:
103:
99:
94:
92:
88:
84:
76:
74:
72:
68:
66:
61:
58:
54:
50:
46:
42:
38:
34:
26:
21:
1075:
1039:
999:
995:
975:
957:
948:
942:
930:
906:
901:
885:(called the
880:
852:
818:
772:
750:
648:
641:
600:
595:
591:
587:
577:
571:
560:
557:pentagrammic
549:
543:
474:
467:
456:
448:
444:
440:
432:
427:
412:, like this
409:
391:
361:
344:
340:
336:
332:
328:
320:
316:
301:simple faces
298:
282:
274:angle defect
267:
255:
183:tetradecagon
128:
124:
120:
117:star polygon
114:
106:
95:
82:
80:
69:
62:
36:
30:
883:4-polytopes
823:v=10, e=15,
643:Edmund Hess
102:turn angles
969:References
777:v=16, e=24
240:dodecagram
1096:Polytopes
1077:MathWorld
1016:0080-4614
949:Polyhedra
833:=2 {5/2},
829:=5 {4}, f
783:=8 {4}, f
699:∑
689:−
657:∑
501:−
364:, like a
327:χ =
252:Polyhedra
238:Isotoxal
202:Heptagram
25:enneagram
1090:Category
915:99-35678
787:=2 {8/2}
455:, where
443:−
331:−
242:, {(6/5)
220:hexagram
217:Isotoxal
185:, {(7/2)
180:Isotoxal
135:Examples
77:Polygons
60:facets.
49:windings
33:geometry
1044:132–134
1032:0062446
433:density
289:squares
37:density
1050:
1030:
1022:
1014:
984:
921:
913:
789:with d
598:= −6.
343:= 2(1-
244:α
224:α
187:α
57:facets
35:, the
1024:91532
1020:JSTOR
893:Notes
839:=1, d
797:=2, d
793:=1, d
431:used
384:genus
313:genus
39:of a
1048:ISBN
1012:ISSN
982:ISBN
919:ISBN
911:LCCN
873:The
853:For
392:zero
366:cube
303:and
285:cube
258:dual
81:The
1004:doi
1000:246
843:=2.
801:=1.
390:is
362:one
339:= 2
323:.
315:is
31:In
1092::
1074:.
1046:,
1028:MR
1026:,
1018:,
1010:,
998:,
917:,
841:f2
837:f1
795:f2
791:f1
594:+
590:−
466:,
447:+
410:-4
386:1
347:).
335:+
93:.
1080:.
1006::
835:d
831:2
827:1
825:f
821:.
819:2
799:v
785:2
781:1
779:f
773:2
737:D
734:2
731:=
726:i
722:f
716:i
713:f
709:d
703:i
695:+
692:e
684:i
680:v
674:i
671:v
667:d
661:i
596:F
592:E
588:V
574:.
572:D
564:v
561:d
553:f
550:d
529:D
526:2
523:=
520:f
515:f
511:d
507:+
504:e
498:v
493:v
489:d
475:D
471:f
468:d
460:v
457:d
449:F
445:E
441:V
439:(
416::
368:.
345:g
341:D
337:F
333:E
329:V
321:g
317:g
129:q
125:q
123:/
121:p
119:{
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.