29:
1097:
458:
937:. Its automorphism group includes symmetries taking any vertex to any other vertex that is on the same side of the bipartition, but none that take a vertex to the other side of the bipartition. Although one can argue directly that the Folkman graph is not vertex-transitive, this can also be explained group-theoretically: its symmetries act
1128:(the minimum number of colors needed to color its edges so that no two edges of the same color meet at a vertex) equals its maximum degree, which in this case is four. For instance, such a coloring can be obtained by using two colors in alternation for each cycle of a Hamiltonian decomposition.
719:
has symmetries taking every half-edge to every other half-edge, the result is edge-transitive. It is not vertex-transitive, because the subdivision vertices are not twins with any other vertex, making them different from the doubled vertices coming
275:
which gave examples of graphs meeting the symmetry condition but not the regularity condition. Folkman's original construction of this graph was a special case of a more general construction of semi-symmetric graphs using
634:
is doubled, replacing it by two vertices with the same neighbors. The ten subdivision vertices form one side of the bipartition of the
Folkman graph, and the ten vertices in twin pairs coming from the doubled vertices of
917:
symmetries. This group acts transitively on the
Folkman graph's edges (it includes a symmetry taking any edge to any other edge) but not on its vertices. The Folkman graph is the smallest undirected graph that is
266:
Semi-symmetric graphs are defined as regular graphs (that is, graphs in which all vertices touch equally many edges) in which each two edges are symmetric to each other, but some two vertices are not symmetric.
1086:
915:
995:. Every symmetry maps a doubled pair of vertices to another doubled pair of vertices, but there is no grouping of the subdivision vertices that is preserved by the symmetries.
751:
Every 4-regular semi-symmetric graph in which some two vertices have the same neighborhood can be constructed in the same way, by subdividing and then doubling a 4-regular
354:
1223:
1176:
993:
966:
873:
846:
780:
747:
717:
690:
660:
632:
605:
578:
543:
516:
489:
452:
426:
400:
819:
1196:
1149:
374:
318:
298:
231:
with symmetries taking every edge to every other edge, but the two sides of its bipartition are not symmetric with each other, making it the smallest possible
1370:
199:
1559:
1455:
271:
was inspired to define and research these graphs in a 1967 paper, after seeing an unpublished manuscript by E. Dauber and
938:
1746:
1005:
1117:
1105:
999:
930:
and were first studied by
Folkman in 1967 who discovered the graph on 20 vertices that now is named after him.
1230:
1417:
Potočnik, Primož; Wilson, Stephen E. (2014), "Linking rings structures and tetravalent semisymmetric graphs",
1751:
1261:
923:
83:
73:
1234:
1198:. However, there are pairs of subdivision vertices from the construction (coming from disjoint edges of
919:
878:
224:
53:
786:. However, there also exist larger 4-regular semi-symmetric graphs that do not have any twin vertices.
1636:"New methods for finding minimum genus embeddings of graphs on orientable and non-orientable surfaces"
1226:
927:
232:
189:
93:
1265:
63:
1512:
Interactions between
Coherent Configurations and Some Classes of Objects in Extremal Combinatorics
1368:; Gronemann, Martin; Kaufmann, Michael; Pupyrev, Sergey (2021), "On dispersable book embeddings",
1723:
1697:
1604:
1453:
Potočnik, Primož; Wilson, Steve (2007), "Tetravalent edge-transitive graphs of girth at most 4",
1379:
795:
277:
243:
103:
1530:
1113:
1101:
323:
179:
1707:
1657:
1647:
1614:
1568:
1464:
1426:
1389:
1365:
1340:
1298:
1121:
113:
1719:
1671:
1582:
1478:
1440:
1401:
1310:
1225:) that are four steps apart from each other. Because the graph contains many 4-cycles, its
1201:
1154:
971:
944:
851:
824:
758:
725:
695:
668:
638:
610:
583:
556:
521:
494:
467:
1715:
1667:
1578:
1474:
1436:
1397:
1306:
1249:
1125:
934:
752:
607:, subdividing each edge into a two-edge path. Then, each of the five original vertices of
255:
228:
169:
143:
133:
123:
1685:
1635:
431:
405:
379:
801:
1631:
1257:
1181:
1134:
550:
462:
359:
303:
283:
251:
247:
174:
1345:
1260:
3, but requires five pages for a "dispersable" book embedding in which each page is a
1740:
1727:
1491:
1269:
220:
184:
1510:
1253:
1242:
1104:. The edges that are not used in this cycle form the second Hamiltonian cycle of a
272:
212:
153:
1534:
1496:
Implementing
Discrete Mathematics: Combinatorics and Graph Theory with Mathematica
1711:
1652:
1554:
1328:
518:, and the red pairs of vertices are the result of doubling the five vertices of
268:
236:
208:
46:
28:
1469:
1431:
1096:
376:, and Folkman uses modular arithmetic to construct a semi-symmetric graph with
250:. Beyond the investigation of its symmetry, it has also been investigated as a
1393:
783:
1539:
1238:
968:, but imprimitively on the vertices constructed by doubling the vertices of
1573:
1302:
457:
1595:
Heule, Marijn; Szeider, Stefan (2015), "A SAT approach to clique-width",
1178:
construction, then all other vertices are at most three steps away from
665:
Because each edge of the result comes from a doubled half of an edge of
1289:
Boesch, F.; Tindell, R. (1984), "Circulants and their connectivities",
1662:
1618:
1229:
is 4, the minimum possible for a bipartite graph. It is also 4-
1702:
1384:
402:
vertices. The
Folkman graph is the result of this construction for
1609:
1095:
456:
875:
ways of swapping some pairs of doubled vertices, for a total of
1557:(1995), "The list chromatic index of a bipartite multigraph",
1120:
into two
Hamiltonian cycles. Like every bipartite graph, its
300:
congruent to 1 mod 4. For each such prime, there is a number
798:
of the
Folkman graph (its group of symmetries) combines the
549:
Another construction for the
Folkman graph begins with the
1498:, Reading, Massachusetts: Addison-Wesley, pp. 186–187
1686:"A practical algorithm for the computation of the genus"
1518:(Doctoral thesis), Ben-Gurion University, pp. 24–25
1204:
1184:
1157:
1137:
1008:
974:
947:
941:
on the vertices constructed as subdivision points of
933:
Like all semi-symmetric graphs, the
Folkman graph is
881:
854:
827:
804:
761:
728:
698:
671:
641:
613:
586:
580:. A new vertex is placed on each of the ten edges of
559:
524:
497:
470:
434:
408:
382:
362:
326:
306:
286:
16:
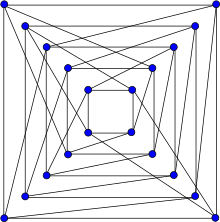
Bipartite 4-regular graph with 20 nodes and 40 edges
1272:need only a number of pages equal to their degree.
162:
152:
142:
132:
122:
112:
102:
92:
82:
72:
62:
52:
42:
21:
1256:, but not on any simpler oriented surface. It has
1217:
1190:
1170:
1143:
1100:The Folkman graph with its vertices arranged in a
1080:
987:
960:
909:
867:
840:
813:
774:
741:
711:
684:
654:
626:
599:
572:
537:
510:
483:
446:
420:
394:
368:
348:
312:
292:
242:The Folkman graph can be constructed either using
1264:, disproving a conjecture of Frank Bernhart and
239:, who constructed it for this property in 1967.
246:or as the subdivided double of the five-vertex
1081:{\displaystyle (x-4)x^{10}(x+4)(x^{2}-6)^{4}}
8:
491:. The green vertices subdivide each edge of
461:Construction of the Folkman graph from the
1131:Its radius is 3 and its diameter is 4. If
27:
1701:
1661:
1651:
1608:
1572:
1468:
1430:
1383:
1344:
1331:(1967), "Regular line-symmetric graphs",
1323:
1321:
1319:
1209:
1203:
1183:
1162:
1156:
1136:
1072:
1056:
1028:
1007:
979:
973:
952:
946:
895:
880:
859:
853:
832:
826:
803:
766:
760:
733:
727:
703:
697:
676:
670:
646:
640:
618:
612:
591:
585:
564:
558:
529:
523:
502:
496:
475:
469:
433:
407:
381:
361:
331:
325:
305:
285:
1364:Alam, Jawaherul Md.; Bekos, Michael A.;
1359:
1357:
1355:
662:form the other side of the bipartition.
1597:ACM Transactions on Computational Logic
1281:
34:
1412:
1410:
1151:is one of the doubled vertices of the
18:
7:
1268:that dispersable book embeddings of
910:{\displaystyle 5!\cdot 2^{5}=3840}
14:
1560:Journal of Combinatorial Theory
1456:Journal of Combinatorial Theory
1333:Journal of Combinatorial Theory
1069:
1049:
1046:
1034:
1021:
1009:
227:and 40 edges. It is a regular
200:Table of graphs and parameters
1:
1690:Ars Mathematica Contemporanea
1640:Ars Mathematica Contemporanea
1419:Ars Mathematica Contemporanea
1346:10.1016/S0021-9800(67)80069-3
1371:Theoretical Computer Science
1712:10.26493/1855-3974.2320.c2d
1653:10.26493/1855-3974.1800.40c
1252:3: it can be embedded on a
1768:
1684:Brinkmann, Gunnar (2022),
1470:10.1016/j.jctb.2006.03.007
1432:10.26493/1855-3974.311.4a8
280:, based on a prime number
1394:10.1016/j.tcs.2021.01.035
1118:Hamiltonian decomposition
1106:Hamiltonian decomposition
1000:characteristic polynomial
926:. Such graphs are called
254:for certain questions of
198:
26:
1634:; Stokes, Klara (2019),
1112:The Folkman graph has a
1002:of the Folkman graph is
349:{\displaystyle r^{2}=-1}
1291:Journal of Graph Theory
1574:10.1006/jctb.1995.1011
1509:Ziv-Av, Matan (2013),
1303:10.1002/jgt.3190080406
1248:The Folkman graph has
1219:
1192:
1172:
1145:
1116:, and more strongly a
1109:
1082:
989:
962:
911:
869:
842:
815:
776:
743:
713:
686:
656:
628:
601:
574:
546:
539:
512:
485:
448:
422:
396:
370:
350:
314:
294:
1220:
1218:{\displaystyle K_{5}}
1193:
1173:
1171:{\displaystyle K_{5}}
1146:
1099:
1083:
990:
988:{\displaystyle K_{5}}
963:
961:{\displaystyle K_{5}}
928:semi-symmetric graphs
922:and regular, but not
912:
870:
868:{\displaystyle 2^{5}}
843:
841:{\displaystyle K_{5}}
816:
777:
775:{\displaystyle K_{5}}
744:
742:{\displaystyle K_{5}}
714:
712:{\displaystyle K_{5}}
687:
685:{\displaystyle K_{5}}
657:
655:{\displaystyle K_{5}}
629:
627:{\displaystyle K_{5}}
602:
600:{\displaystyle K_{5}}
575:
573:{\displaystyle K_{5}}
540:
538:{\displaystyle K_{5}}
513:
511:{\displaystyle K_{5}}
486:
484:{\displaystyle K_{5}}
460:
449:
423:
397:
371:
351:
315:
295:
1202:
1182:
1155:
1135:
1006:
972:
945:
879:
852:
825:
802:
790:Algebraic properties
782:or the graph of the
759:
726:
696:
669:
639:
611:
584:
557:
522:
495:
468:
432:
406:
380:
360:
324:
304:
284:
235:. It is named after
233:semi-symmetric graph
447:{\displaystyle r=2}
421:{\displaystyle p=5}
395:{\displaystyle 2pr}
1696:(4), Paper No. 1,
1531:Weisstein, Eric W.
1215:
1188:
1168:
1141:
1110:
1078:
985:
958:
907:
865:
838:
814:{\displaystyle 5!}
811:
796:automorphism group
772:
739:
709:
682:
652:
624:
597:
570:
553:on five vertices,
547:
535:
508:
481:
444:
418:
392:
366:
346:
310:
290:
278:modular arithmetic
244:modular arithmetic
33:Drawing following
1747:Individual graphs
1603:(3): 24:1–24:27,
1191:{\displaystyle v}
1144:{\displaystyle v}
1114:Hamiltonian cycle
1102:Hamiltonian cycle
924:vertex-transitive
369:{\displaystyle p}
313:{\displaystyle r}
293:{\displaystyle p}
205:
204:
1759:
1731:
1730:
1705:
1681:
1675:
1674:
1665:
1655:
1628:
1622:
1621:
1612:
1592:
1586:
1585:
1576:
1551:
1545:
1544:
1543:
1526:
1520:
1519:
1517:
1506:
1500:
1499:
1488:
1482:
1481:
1472:
1450:
1444:
1443:
1434:
1414:
1405:
1404:
1387:
1361:
1350:
1349:
1348:
1325:
1314:
1313:
1286:
1231:vertex-connected
1224:
1222:
1221:
1216:
1214:
1213:
1197:
1195:
1194:
1189:
1177:
1175:
1174:
1169:
1167:
1166:
1150:
1148:
1147:
1142:
1124:is two, and its
1122:chromatic number
1092:Other properties
1087:
1085:
1084:
1079:
1077:
1076:
1061:
1060:
1033:
1032:
994:
992:
991:
986:
984:
983:
967:
965:
964:
959:
957:
956:
916:
914:
913:
908:
900:
899:
874:
872:
871:
866:
864:
863:
847:
845:
844:
839:
837:
836:
820:
818:
817:
812:
781:
779:
778:
773:
771:
770:
750:
748:
746:
745:
740:
738:
737:
718:
716:
715:
710:
708:
707:
691:
689:
688:
683:
681:
680:
661:
659:
658:
653:
651:
650:
633:
631:
630:
625:
623:
622:
606:
604:
603:
598:
596:
595:
579:
577:
576:
571:
569:
568:
544:
542:
541:
536:
534:
533:
517:
515:
514:
509:
507:
506:
490:
488:
487:
482:
480:
479:
453:
451:
450:
445:
427:
425:
424:
419:
401:
399:
398:
393:
375:
373:
372:
367:
355:
353:
352:
347:
336:
335:
319:
317:
316:
311:
299:
297:
296:
291:
114:Chromatic number
31:
19:
1767:
1766:
1762:
1761:
1760:
1758:
1757:
1756:
1737:
1736:
1735:
1734:
1683:
1682:
1678:
1632:Conder, Marston
1630:
1629:
1625:
1619:10.1145/2736696
1594:
1593:
1589:
1553:
1552:
1548:
1535:"Folkman Graph"
1529:
1528:
1527:
1523:
1515:
1508:
1507:
1503:
1490:
1489:
1485:
1452:
1451:
1447:
1416:
1415:
1408:
1363:
1362:
1353:
1327:
1326:
1317:
1288:
1287:
1283:
1278:
1205:
1200:
1199:
1180:
1179:
1158:
1153:
1152:
1133:
1132:
1126:chromatic index
1094:
1068:
1052:
1024:
1004:
1003:
975:
970:
969:
948:
943:
942:
920:edge-transitive
891:
877:
876:
855:
850:
849:
828:
823:
822:
800:
799:
792:
762:
757:
756:
753:symmetric graph
729:
724:
723:
721:
699:
694:
693:
672:
667:
666:
642:
637:
636:
614:
609:
608:
587:
582:
581:
560:
555:
554:
525:
520:
519:
498:
493:
492:
471:
466:
465:
430:
429:
404:
403:
378:
377:
358:
357:
327:
322:
321:
302:
301:
282:
281:
264:
256:graph embedding
229:bipartite graph
194:
124:Chromatic index
38:
17:
12:
11:
5:
1765:
1763:
1755:
1754:
1752:Regular graphs
1749:
1739:
1738:
1733:
1732:
1676:
1623:
1587:
1567:(1): 153–158,
1546:
1521:
1501:
1492:Skiena, Steven
1483:
1463:(2): 217–236,
1445:
1425:(2): 341–352,
1406:
1366:Dujmović, Vida
1351:
1339:(3): 215–232,
1315:
1297:(4): 487–499,
1280:
1279:
1277:
1274:
1270:regular graphs
1258:book thickness
1235:edge-connected
1212:
1208:
1187:
1165:
1161:
1140:
1093:
1090:
1075:
1071:
1067:
1064:
1059:
1055:
1051:
1048:
1045:
1042:
1039:
1036:
1031:
1027:
1023:
1020:
1017:
1014:
1011:
982:
978:
955:
951:
906:
903:
898:
894:
890:
887:
884:
862:
858:
835:
831:
821:symmetries of
810:
807:
791:
788:
769:
765:
736:
732:
706:
702:
692:, and because
679:
675:
649:
645:
621:
617:
594:
590:
567:
563:
551:complete graph
532:
528:
505:
501:
478:
474:
463:complete graph
443:
440:
437:
417:
414:
411:
391:
388:
385:
365:
345:
342:
339:
334:
330:
309:
289:
263:
260:
252:counterexample
248:complete graph
223:graph with 20
203:
202:
196:
195:
193:
192:
190:Semi-symmetric
187:
182:
177:
172:
166:
164:
160:
159:
156:
150:
149:
146:
144:Book thickness
140:
139:
136:
130:
129:
126:
120:
119:
116:
110:
109:
106:
100:
99:
96:
90:
89:
86:
80:
79:
76:
70:
69:
66:
60:
59:
56:
50:
49:
44:
40:
39:
35:Folkman (1967)
32:
24:
23:
15:
13:
10:
9:
6:
4:
3:
2:
1764:
1753:
1750:
1748:
1745:
1744:
1742:
1729:
1725:
1721:
1717:
1713:
1709:
1704:
1699:
1695:
1691:
1687:
1680:
1677:
1673:
1669:
1664:
1659:
1654:
1649:
1645:
1641:
1637:
1633:
1627:
1624:
1620:
1616:
1611:
1606:
1602:
1598:
1591:
1588:
1584:
1580:
1575:
1570:
1566:
1562:
1561:
1556:
1550:
1547:
1542:
1541:
1536:
1532:
1525:
1522:
1514:
1513:
1505:
1502:
1497:
1493:
1487:
1484:
1480:
1476:
1471:
1466:
1462:
1458:
1457:
1449:
1446:
1442:
1438:
1433:
1428:
1424:
1420:
1413:
1411:
1407:
1403:
1399:
1395:
1391:
1386:
1381:
1377:
1373:
1372:
1367:
1360:
1358:
1356:
1352:
1347:
1342:
1338:
1334:
1330:
1324:
1322:
1320:
1316:
1312:
1308:
1304:
1300:
1296:
1292:
1285:
1282:
1275:
1273:
1271:
1267:
1263:
1259:
1255:
1251:
1246:
1244:
1240:
1236:
1232:
1228:
1210:
1206:
1185:
1163:
1159:
1138:
1129:
1127:
1123:
1119:
1115:
1107:
1103:
1098:
1091:
1089:
1073:
1065:
1062:
1057:
1053:
1043:
1040:
1037:
1029:
1025:
1018:
1015:
1012:
1001:
996:
980:
976:
953:
949:
940:
936:
931:
929:
925:
921:
904:
901:
896:
892:
888:
885:
882:
860:
856:
833:
829:
808:
805:
797:
789:
787:
785:
767:
763:
754:
734:
730:
704:
700:
677:
673:
663:
647:
643:
619:
615:
592:
588:
565:
561:
552:
530:
526:
503:
499:
476:
472:
464:
459:
455:
441:
438:
435:
415:
412:
409:
389:
386:
383:
363:
343:
340:
337:
332:
328:
307:
287:
279:
274:
270:
261:
259:
257:
253:
249:
245:
240:
238:
234:
230:
226:
222:
218:
217:Folkman graph
214:
210:
201:
197:
191:
188:
186:
183:
181:
178:
176:
173:
171:
168:
167:
165:
161:
157:
155:
151:
147:
145:
141:
137:
135:
131:
127:
125:
121:
117:
115:
111:
108:5! · 2 = 3840
107:
105:
104:Automorphisms
101:
97:
95:
91:
87:
85:
81:
77:
75:
71:
67:
65:
61:
57:
55:
51:
48:
45:
41:
36:
30:
25:
22:Folkman graph
20:
1693:
1689:
1679:
1643:
1639:
1626:
1600:
1596:
1590:
1564:
1563:, Series B,
1558:
1555:Galvin, Fred
1549:
1538:
1524:
1511:
1504:
1495:
1486:
1460:
1459:, Series B,
1454:
1448:
1422:
1418:
1375:
1369:
1336:
1332:
1294:
1290:
1284:
1254:triple torus
1247:
1245:are both 5.
1243:clique-width
1130:
1111:
997:
932:
793:
664:
548:
273:Frank Harary
265:
262:Construction
241:
216:
213:graph theory
209:mathematical
206:
154:Queue number
1646:(1): 1–35,
1329:Folkman, J.
1266:Paul Kainen
939:primitively
269:Jon Folkman
237:Jon Folkman
180:Hamiltonian
47:Jon Folkman
43:Named after
1741:Categories
1703:2005.08243
1663:2292/57926
1385:1803.10030
1276:References
784:octahedron
320:such that
163:Properties
37:, Figure 1
1728:218674244
1610:1304.5498
1540:MathWorld
1239:treewidth
1063:−
1016:−
935:bipartite
889:⋅
848:with the
341:−
211:field of
170:Bipartite
1494:(1990),
1378:: 1–22,
1262:matching
755:such as
225:vertices
175:Eulerian
84:Diameter
54:Vertices
1720:4498572
1672:3992757
1583:1309363
1479:2290322
1441:3240442
1402:4221556
1311:0766498
221:regular
219:is a 4-
207:In the
185:Regular
1726:
1718:
1670:
1581:
1477:
1439:
1400:
1309:
1237:. Its
1233:and 4-
215:, the
74:Radius
1724:S2CID
1698:arXiv
1605:arXiv
1516:(PDF)
1380:arXiv
1250:genus
1227:girth
722:from
134:Genus
94:Girth
64:Edges
1241:and
998:The
905:3840
794:The
428:and
356:mod
1708:doi
1658:hdl
1648:doi
1615:doi
1569:doi
1465:doi
1427:doi
1390:doi
1376:861
1341:doi
1299:doi
1743::
1722:,
1716:MR
1714:,
1706:,
1694:22
1692:,
1688:,
1668:MR
1666:,
1656:,
1644:17
1642:,
1638:,
1613:,
1601:16
1599:,
1579:MR
1577:,
1565:63
1537:,
1533:,
1475:MR
1473:,
1461:97
1437:MR
1435:,
1421:,
1409:^
1398:MR
1396:,
1388:,
1374:,
1354:^
1335:,
1318:^
1307:MR
1305:,
1293:,
1088:.
1030:10
454:.
258:.
68:40
58:20
1710::
1700::
1660::
1650::
1617::
1607::
1571::
1467::
1429::
1423:7
1392::
1382::
1343::
1337:3
1301::
1295:8
1211:5
1207:K
1186:v
1164:5
1160:K
1139:v
1108:.
1074:4
1070:)
1066:6
1058:2
1054:x
1050:(
1047:)
1044:4
1041:+
1038:x
1035:(
1026:x
1022:)
1019:4
1013:x
1010:(
981:5
977:K
954:5
950:K
902:=
897:5
893:2
886:!
883:5
861:5
857:2
834:5
830:K
809:!
806:5
768:5
764:K
749:.
735:5
731:K
705:5
701:K
678:5
674:K
648:5
644:K
620:5
616:K
593:5
589:K
566:5
562:K
545:.
531:5
527:K
504:5
500:K
477:5
473:K
442:2
439:=
436:r
416:5
413:=
410:p
390:r
387:p
384:2
364:p
344:1
338:=
333:2
329:r
308:r
288:p
158:2
148:3
138:3
128:4
118:2
98:4
88:4
78:3
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.