667:. The irrational angle formed on the chromatic circle by a perfect fifth is close to 7/12 of a circle, and therefore the twelve tones of the Pythagorean tuning are close to, but not the same as, the twelve tones of equal temperament, which could be generated in the same way using an angle of exactly 7/12 of a circle. Instead of being spaced at angles of exactly 1/12 of a circle, as the tones of equal temperament would be, the tones of the Pythagorean tuning are separated by intervals of two different angles, close to but not exactly 1/12 of a circle, representing two different types of
688:
390:
331:
353:
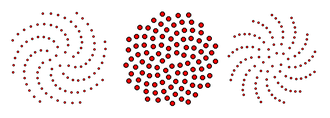
349:, approximately 137.5°. It has been suggested that this angle maximizes the sun-collecting power of the plant's leaves. If one looks end-on at a plant stem that has grown in this way, there will be at most three distinct angles between two leaves that are consecutive in the cyclic order given by this end-on view.
707:
is infinite sequences of two symbols (for instance, "H" and "V") describing the sequence of horizontal and vertical reflections of a light ray within a mirrored square, starting along a line of irrational slope. Equivalently, the same sequence describes the sequence of horizontal and vertical lines
678:
In this context, the three-gap theorem can be used to describe any tuning system that is generated in this way by consecutive multiples of a single interval. Some of these tuning systems (like equal temperament) may have only one interval separating the closest pairs of tones, and some (like the
364:
For example, in the figure, the largest of these three angles occurs three times, between the leaves numbered 3 and 6, between leaves 4 and 7, and between leaves 5 and 8. The second-largest angle occurs five times, between leaves 6 and 1, 9 and 4, 7 and 2, 10 and 5, and 8 and 3. And the smallest
909:
is a gap. So there can be at most three rigid gaps, the two on either side of the last point and the one in which the predecessor of the first point (if it were part of the sequence) would land. Because there are at most three rigid gaps, there are at most three lengths of gaps.
365:
angle occurs only twice, between leaves 1 and 9 and between leaves 2 and 10. The phenomenon of having three types of distinct gaps depends only on fact that the growth pattern uses a constant rotation angle, and not on the relation of this angle to the
57:, ... from the starting point, then there will be at most three distinct distances between pairs of points in adjacent positions around the circle. When there are three distances, the largest of the three always equals the sum of the other two. Unless
1666:
as a definition of
Sturmian words, rather than as a consequence of the definition. For the equivalence of this property with the definition stated here, see Theorem 2.1.13, p. 51. For the three frequencies of these words see Theorem 2.2.37, p.
369:; the same phenomenon would happen for any other rotation angle, and not just for the golden angle. However, other properties of this growth pattern do depend on the golden ratio. For instance, the fact that golden ratio is a
261:
into subintervals with at most three different lengths. The two problems are equivalent under a linear correspondence between the unit interval and the circumference of the circle, and a correspondence between the real number
730:
subsequences occur with at most three distinct frequencies. If there are three frequencies, then the largest frequency must equal the sum of the other two. One proof of this result involves partitioning the
93:; more proofs were added by others later. Applications of the three-gap theorem include the study of plant growth and musical tuning systems, and the theory of light reflection within a mirrored square.
2516:
2302:
2197:
1958:
671:. If the Pythagorean tuning system were extended by one more perfect fifth, to a set of 13 tones, then the sequence of intervals between its tones would include a third, much shorter interval, the
1716:
1954:
165:
from the starting point, then there will be at most three distinct distances between pairs of points in adjacent positions around the circle. An equivalent and more algebraic form involves the
679:
Pythagorean tuning) may have only two different intervals separating the tones, but the three-gap theorem implies that there are always at most three different intervals separating the tones.
255:
163:
2595:
445:
corresponds to the ratio 3:2. Two tones are commonly considered to be equivalent when they differ by a whole number of octaves; this equivalence can be represented geometrically by the
590:
between points on this circle, meaning that two musical tones differ by the given interval when their two points on the circle differ by this angle. For instance, this formula gives
529:
314:
2193:
588:
2512:
1404:
Baroin, Gilles; Calvet, André (2019), "Visualizing temperaments: squaring the circle?", in
Montiel, Mariana; Gomez-Martin, Francisco; Agustín-Aquino, Octavio A. (eds.),
918:
Liang's proof additionally shows that, when there are exactly three gap lengths, the longest gap length is the sum of the other two. For, in this case, the rotated copy
1796:
280:
191:
1291:
638:
611:
549:
928:
that has the first point in it is partitioned by that point into two smaller gaps, which must be the other two gaps. Liang also proves a more general result, the "
475:
1644:
1224:
2378:
992:
949:
2483:
2102:
Bleher, Pavel M.; Homma, Youkow; Ji, Lyndon L.; Roeder, Roland K. W.; Shen, Jeffrey D. (2012), "Nearest neighbor distances on a circle: multidimensional case",
1664:
969:
345:, the arrangements of leaves on plant stems, it has been observed that each successive leaf on the stems of many plants is turned from the previous leaf by the
211:
119:
655:
is a tuning system, consisting of 12 tones equally spaced around the chromatic circle. Some other tuning systems do not space their tones equally, but instead
1606:
1123:
855:
is not a gap, because it has the same length and would be one step later. The only ways for this to happen are for one of the endpoints of
708:
of the integer grid that are crossed by the starting line. One property that all such sequences have is that, for any positive integer
1029:
has at most three lengths of gaps between sequence values. Again, if there are three gap lengths then one is the sum of the other two.
2627:
2622:
780:. Later researchers published additional proofs, generalizing this result to higher dimensions, and connecting it to topics including
2423:
1569:
1509:
1483:
1389:
1274:
1151:
1078:
1687:
994:
different gap lengths. In the three-gap theorem, there is a constant bound on the ratios between the three gaps, if and only if
2002:
841:
than any other gap of the same length. From this definition, it follows that every gap has the same length as a rigid gap. If
2382:
437:. Intervals are commonly considered consonant or harmonious when they are the ratio of two small integers; for instance, the
101:
The three-gap theorem can be stated geometrically in terms of points on a circle. In this form, it states that if one places
2632:
1836:
1406:
Mathematics and
Computation in Music: 7th International Conference, MCM 2019, Madrid, Spain, June 18–21, 2019, Proceedings
777:
90:
771:
84:
1893:
1760:
The first proofs of this remarkable fact were published in 1957 by Sós, in 1958 by Surányi, and in 1959 by Świerczkowski
1260:
663:, which is constructed in this way from twelve tones, generated as the consecutive multiples of a perfect fifth in the
216:
124:
2561:
1098:
Types for Proofs and
Programs: International Workshop, TYPES'99, Lökeberg, Sweden, June 12–16, 1999, Selected Papers
1598:
723:. Each subsequence occurs infinitely often with a certain frequency, and the three-gap theorem implies that these
1714:
Haynes, Alan; Marklof, Jens (2020), "Higher dimensional
Steinhaus and Slater problems via homogeneous dynamics",
1005:
449:, the points of which represent classes of equivalent tones. Mathematically, this circle can be described as the
370:
2048:
1043:
1038:
1841:
640:, and similarly other common musical intervals other than the octave do not correspond to rational angles.
480:
1324:
287:
2165:
554:
457:, and the point on this circle that represents a given tone can be obtained by the mapping the frequency
2488:
2311:
2121:
1678:
1343:
1182:
656:
1588:
2241:
1469:
1190:
789:
766:
687:
79:
1592:
617:, the angle on the chromatic circle that represents a perfect fifth is not a rational multiple of
2541:
2448:
2335:
2276:
2250:
2222:
2145:
2111:
2085:
2057:
2029:
1983:
1880:, from which the following classification of these proofs and many of their references are taken.
1751:
1725:
1541:
1451:
1417:
1359:
1333:
1202:
1186:
1160:
1149:
Marklof, Jens; Strömbergsson, Andreas (2017), "The three gap theorem and the space of lattices",
1129:
1101:
781:
660:
394:
831:
of the circle that extends between two adjacent points of the given set, and define a gap to be
1524:
Carey, Norman (2007), "Coherence and sameness in well-formed and pairwise well-formed scales",
1377:
389:
1778:
1602:
1565:
1505:
1479:
1473:
1385:
1270:
1119:
1074:
699:, there are four distinct length-3 subsequences (in left-right order): 010, 100, 001, and 101.
672:
648:
414:
405:
used to construct the tuning; the two longer gap lengths between consecutive points represent
1559:
1499:
1264:
1068:
749:
elements of the sequence are the same, and applying the three-gap theorem to this partition.
265:
176:
2525:
2432:
2391:
2319:
2260:
2206:
2129:
2067:
2011:
1967:
1850:
1735:
1612:
1533:
1443:
1409:
1351:
1300:
1233:
1178:
1170:
1111:
1016:
817:
be the rotation angle generating a set of points as some number of consecutive multiples of
664:
446:
426:
398:
2537:
2444:
2405:
2331:
2272:
2218:
2141:
2081:
2025:
1979:
1864:
1747:
1700:
1247:
1198:
620:
593:
534:
2533:
2440:
2401:
2327:
2268:
2239:
Biringer, Ian; Schmidt, Benjamin (2008), "The three gap theorem and
Riemannian geometry",
2214:
2137:
2077:
2021:
1975:
1860:
1743:
1696:
1616:
1243:
1194:
1064:
460:
330:
166:
1623:
2360:
2315:
2125:
1347:
1174:
974:
931:
613:(a whole circle) as the angle corresponding to an octave. Because 3/2 is not a rational
2468:
1772:
1649:
954:
805:
793:
762:
758:
692:
196:
104:
75:
71:
2616:
2545:
2452:
2396:
2226:
2089:
2033:
1987:
1704:; see in particular Section 2.1, "Complexity and frequencies of codings of rotations"
1545:
1421:
1363:
1206:
1011:
A closely related but earlier theorem, also called the three-gap theorem, is that if
704:
696:
644:
454:
442:
402:
374:
357:
258:
2339:
1755:
659:
them by some number of consecutive multiples of a given interval. An example is the
2280:
1133:
614:
434:
422:
366:
346:
335:
2436:
2149:
1817:
Surányi, J. (1958), "Über die
Anordnung der Vielfachen einer reelen Zahl mod 1",
1561:
Microtonality and the Tuning
Systems of Erv Wilson: Mapping the Harmonic Spectrum
1413:
1100:, Lecture Notes in Computer Science, vol. 1956, Springer, pp. 162–173,
1584:
1434:
Carey, Norman; Clampitt, David (October 1989), "Aspects of well-formed scales",
1384:, Southwestern College, Winfield, Kansas: Bridges Conference, pp. 101–110,
1322:
Akiyama, Shigeki (March 2020), "Spiral Delone sets and three distance theorem",
797:
732:
450:
342:
170:
1355:
352:
2529:
2323:
2264:
2210:
2133:
2072:
1971:
1537:
1305:
1238:
410:
378:
1839:(1959), "On successive settings of an arc on the circumference of a circle",
1682:
1222:
van
Ravenstein, Tony (1988), "The three-gap theorem (Steinhaus conjecture)",
1115:
334:
End-on view of a plant stem in which consecutive leaves are separated by the
2000:
Chevallier, Nicolas (2007), "Cyclic groups and the three distance theorem",
1855:
430:
2016:
647:
is a collection of tones used to compose and play music. For instance, the
2294:
1378:"The mathematics of the just intonation used in the music of Terry Riley"
785:
668:
406:
1739:
1096:
Mayero, Micaela (2000), "The three gap theorem (Steinhaus conjecture)",
1475:
Music as
Concept and Practice in the Late Middle Ages, Volume 3, Part 1
2293:
Haynes, Alan; Koivusalo, Henna; Walton, James; Sadun, Lorenzo (2016),
1455:
901:, because otherwise its predecessor in the sequence would land within
2062:
1478:, New Oxford history of music, Oxford University Press, p. 252,
438:
1730:
1447:
1338:
1165:
1106:
2295:"Gaps problems and frequencies of patches in cut and project sets"
2255:
2116:
686:
652:
388:
351:
329:
1289:
van Ravenstein, Tony (1987), "Number sequences and phyllotaxis",
2558:
Florek, K. (1951), "Une remarque sur la répartition des nombres
1564:, Routledge Studies in Music Theory, Routledge, pp. 90–91,
2517:
Mathematical Proceedings of the Cambridge Philosophical Society
2303:
Mathematical Proceedings of the Cambridge Philosophical Society
2198:
Mathematical Proceedings of the Cambridge Philosophical Society
2046:
Vijay, Sujith (2008), "Eleven Euclidean distances are enough",
1959:
Mathematical Proceedings of the Cambridge Philosophical Society
885:, preventing it from being a gap. A point can only land within
2176:
835:
if its endpoints occur later in the sequence of multiples of
2421:
Shiu, Peter (2018), "A footnote to the three gaps theorem",
1382:
Bridges: Mathematical Connections in Art, Music, and Science
1890:
Halton, John H. (1965), "The distribution of the sequence
1070:
Automatic Sequences: Theory, Applications, Generalizations
971:
different arithmetic progressions on a circle has at most
875:
is missing) or for one of the given points to land within
381:; intuitively, this means that they are uniformly spaced.
2162:
Slater, Noel B. (1967), "Gaps and steps for the sequence
895:
if it is the first point in the sequence of multiples of
360:(center) are more uniformly spaced than for other angles.
2465:
Slater, N. B. (1950), "The distribution of the integers
1408:, Springer International Publishing, pp. 333–337,
761:, and its first proofs were found in the late 1950s by
811:
The following simple proof is due to Frank Liang. Let
483:
67:, there will also be at least two distinct distances.
2564:
2491:
2471:
2363:
2168:
1896:
1781:
1652:
1626:
977:
957:
934:
859:
to be the last point in the sequence of multiples of
623:
596:
557:
537:
463:
290:
268:
219:
199:
179:
127:
107:
1877:
1876:
These proofs are briefly surveyed and classified by
1683:"Three distance theorems and combinatorics on words"
377:(as they are in some models of plant growth) form a
1775:(1958), "On the distribution mod 1 of the sequence
1717:
Annales Scientifiques de l'École Normale Supérieure
951:distance theorem", according to which the union of
373:implies that points spaced at this angle along the
2589:
2506:
2477:
2372:
2187:
1949:{\displaystyle \{n\xi \}\,(n=0,\,1,\,2,\,\ldots )}
1948:
1790:
1658:
1638:
986:
963:
943:
632:
605:
582:
543:
523:
469:
308:
274:
249:
205:
185:
157:
113:
250:{\displaystyle \alpha ,2\alpha ,\dots ,n\alpha }
158:{\displaystyle \theta ,2\theta ,\dots ,n\theta }
1292:Bulletin of the Australian Mathematical Society
173:. It states that, for any positive real number
2590:{\displaystyle n\xi \,(\operatorname {mod} 1)}
2357:Liang, Frank M. (1979), "A short proof of the
1269:, Princeton University Press, pp. 35–41,
1225:Journal of the Australian Mathematical Society
1073:, Cambridge University Press, pp. 53–55,
8:
1906:
1897:
1819:Ann. Univ. Sci. Budapest, Eötvös Sect. Math.
1800:Ann. Univ. Sci. Budapest, Eötvös Sect. Math.
1501:A Smoother Pebble: Mathematical Explorations
719:distinct consecutive subsequences of length
1067:(2003), "2.6 The Three-Distance Theorem",
356:Points spaced at the golden angle along a
2571:
2563:
2490:
2470:
2395:
2362:
2254:
2179:
2175:
2167:
2115:
2071:
2061:
2015:
1939:
1932:
1925:
1909:
1895:
1854:
1780:
1729:
1651:
1625:
1337:
1317:
1315:
1304:
1237:
1183:1983/b5fd0feb-e42d-48e9-94d8-334b8dc24505
1164:
1105:
976:
956:
933:
757:The three-gap theorem was conjectured by
622:
595:
568:
556:
536:
506:
482:
462:
289:
267:
218:
198:
178:
126:
106:
2352:
2350:
2348:
1091:
1089:
441:corresponds to the ratio 2:1, while the
2416:
2414:
1620:. Lothaire uses the property of having
1504:, Oxford University Press, p. 51,
1055:
865:(so that the corresponding endpoint of
18:On distances between points on a circle
1217:
1215:
801:
745:subintervals within which the initial
738:of the starting lines (modulo 1) into
524:{\textstyle \exp(2\pi i\log _{2}\nu )}
213:, the fractional parts of the numbers
7:
1144:
1142:
905:, contradicting the assumption that
309:{\displaystyle \theta =2\pi \alpha }
2188:{\displaystyle n\theta {\bmod {1}}}
1191:10.4169/amer.math.monthly.124.8.741
1175:10.4169/amer.math.monthly.124.8.741
1015:is any arc of the circle, then the
583:{\displaystyle 2\pi \log _{2}\rho }
1878:Marklof & Strömbergsson (2017)
14:
2507:{\displaystyle \theta N<\phi }
2424:The American Mathematical Monthly
1152:The American Mathematical Monthly
121:points on a circle, at angles of
37:points on a circle, at angles of
1594:Algebraic Combinatorics on Words
1526:Journal of Mathematics and Music
2003:Canadian Journal of Mathematics
70:This result was conjectured by
2584:
2572:
2104:Journal of Statistical Physics
1943:
1910:
518:
490:
409:, and the short gap where the
1:
2437:10.1080/00029890.2018.1412210
804:formalizes a proof using the
74:, and proved in the 1950s by
2397:10.1016/0012-365X(79)90140-7
1414:10.1007/978-3-030-21392-3_27
808:interactive theorem prover.
1688:L'Enseignement mathématique
1380:, in Sarhangi, Reza (ed.),
712:, the sequence has exactly
2649:
1599:Cambridge University Press
1558:Narushima, Terumi (2017),
1498:Benson, Donald C. (2003),
1266:A Mathematical Nature Walk
63:is a rational multiple of
33:states that if one places
2628:Theorems in number theory
2623:Diophantine approximation
2530:10.1017/S0305004100026086
2324:10.1017/S0305004116000128
2265:10.1007/s10711-008-9283-8
2211:10.1017/S0305004100042195
2134:10.1007/s10955-011-0367-8
2073:10.1016/j.jnt.2007.08.016
1972:10.1017/S0305004100039013
1538:10.1080/17459730701376743
1306:10.1017/s0004972700026605
1239:10.1017/S1446788700031062
1006:badly approximable number
551:corresponds to the angle
531:. An interval with ratio
413:fails to close up is the
371:badly approximable number
2049:Journal of Number Theory
1791:{\displaystyle n\alpha }
1356:10.1088/1361-6544/ab74ad
1116:10.1007/3-540-44557-9_10
1044:Lonely runner conjecture
1039:Equidistribution theorem
798:space of planar lattices
2599:Colloquium Mathematicum
1856:10.4064/fm-46-2-187-189
1842:Fundamenta Mathematicae
1376:Haack, Joel K. (1999),
778:Stanisław Świerczkowski
429:describes the ratio in
275:{\displaystyle \alpha }
186:{\displaystyle \alpha }
91:Stanisław Świerczkowski
2591:
2508:
2479:
2374:
2189:
2017:10.4153/CJM-2007-022-3
1950:
1792:
1660:
1640:
988:
965:
945:
823:on a circle. Define a
700:
651:commonly used for the
634:
607:
584:
545:
525:
477:to the complex number
471:
418:
361:
338:
310:
276:
251:
207:
187:
159:
115:
27:three-distance theorem
2592:
2509:
2480:
2375:
2190:
1951:
1793:
1661:
1641:
1436:Music Theory Spectrum
1063:Allouche, Jean-Paul;
989:
966:
946:
845:is a rigid gap, then
690:
635:
633:{\displaystyle 2\pi }
608:
606:{\displaystyle 2\pi }
585:
546:
544:{\displaystyle \rho }
526:
472:
401:. Edges indicate the
392:
355:
333:
311:
277:
252:
208:
188:
160:
116:
2633:Mathematics of music
2562:
2489:
2469:
2383:Discrete Mathematics
2361:
2166:
1894:
1779:
1677:Alessandri, Pascal;
1650:
1624:
1470:Blackburn, Bonnie J.
975:
955:
932:
790:Riemannian manifolds
621:
594:
555:
535:
481:
470:{\displaystyle \nu }
461:
288:
266:
217:
197:
177:
125:
105:
31:Steinhaus conjecture
21:In mathematics, the
2380:distance theorem",
2316:2016MPCPS.161...65H
2242:Geometriae Dedicata
2126:2012JSP...146..446B
1740:10.24033/asens.2427
1639:{\displaystyle d+1}
1348:2020Nonli..33.2533A
782:continued fractions
683:Mirrored reflection
2587:
2504:
2475:
2373:{\displaystyle 3d}
2370:
2185:
1946:
1788:
1656:
1636:
1601:, pp. 40–97,
1468:Strohm, Reinhard;
987:{\displaystyle 3d}
984:
961:
944:{\displaystyle 3d}
941:
701:
695:, an example of a
661:Pythagorean tuning
630:
603:
580:
541:
521:
467:
419:
395:Pythagorean tuning
362:
339:
306:
272:
247:
203:
183:
169:of multiples of a
155:
111:
2478:{\displaystyle N}
1837:Świerczkowski, S.
1659:{\displaystyle d}
1608:978-0-521-81220-7
1125:978-3-540-41517-6
964:{\displaystyle d}
784:, symmetries and
753:History and proof
673:Pythagorean comma
649:equal temperament
415:Pythagorean comma
397:as points of the
206:{\displaystyle n}
114:{\displaystyle n}
23:three-gap theorem
2640:
2607:
2606:
2596:
2594:
2593:
2588:
2555:
2549:
2548:
2513:
2511:
2510:
2505:
2484:
2482:
2481:
2476:
2462:
2456:
2455:
2418:
2409:
2408:
2399:
2379:
2377:
2376:
2371:
2354:
2343:
2342:
2299:
2290:
2284:
2283:
2258:
2236:
2230:
2229:
2205:(4): 1115–1123,
2194:
2192:
2191:
2186:
2184:
2183:
2159:
2153:
2152:
2119:
2099:
2093:
2092:
2075:
2065:
2056:(6): 1655–1661,
2043:
2037:
2036:
2019:
1997:
1991:
1990:
1955:
1953:
1952:
1947:
1887:
1881:
1874:
1868:
1867:
1858:
1833:
1827:
1826:
1814:
1808:
1807:
1797:
1795:
1794:
1789:
1769:
1763:
1762:
1733:
1711:
1705:
1703:
1695:(1–2): 103–132,
1674:
1668:
1665:
1663:
1662:
1657:
1646:words of length
1645:
1643:
1642:
1637:
1619:
1589:"Sturmian Words"
1581:
1575:
1574:
1555:
1549:
1548:
1521:
1515:
1514:
1495:
1489:
1488:
1465:
1459:
1458:
1431:
1425:
1424:
1401:
1395:
1394:
1373:
1367:
1366:
1341:
1332:(5): 2533–2540,
1319:
1310:
1309:
1308:
1286:
1280:
1279:
1257:
1251:
1250:
1241:
1219:
1210:
1209:
1168:
1146:
1137:
1136:
1109:
1093:
1084:
1083:
1065:Shallit, Jeffrey
1060:
1028:
1024:
1019:of multiples of
1017:integer sequence
1014:
1003:
1002:
993:
991:
990:
985:
970:
968:
967:
962:
950:
948:
947:
942:
927:
908:
904:
900:
894:
884:
874:
864:
858:
854:
844:
840:
830:
822:
816:
775:
748:
744:
735:
729:
722:
718:
711:
665:circle of fifths
639:
637:
636:
631:
612:
610:
609:
604:
589:
587:
586:
581:
573:
572:
550:
548:
547:
542:
530:
528:
527:
522:
511:
510:
476:
474:
473:
468:
447:chromatic circle
427:musical interval
399:chromatic circle
341:In the study of
317:
315:
313:
312:
307:
281:
279:
278:
273:
256:
254:
253:
248:
212:
210:
209:
204:
192:
190:
189:
184:
167:fractional parts
164:
162:
161:
156:
120:
118:
117:
112:
88:
66:
62:
56:
49:
42:
36:
2648:
2647:
2643:
2642:
2641:
2639:
2638:
2637:
2613:
2612:
2611:
2610:
2560:
2559:
2557:
2556:
2552:
2487:
2486:
2467:
2466:
2464:
2463:
2459:
2420:
2419:
2412:
2359:
2358:
2356:
2355:
2346:
2297:
2292:
2291:
2287:
2238:
2237:
2233:
2164:
2163:
2161:
2160:
2156:
2101:
2100:
2096:
2045:
2044:
2040:
1999:
1998:
1994:
1892:
1891:
1889:
1888:
1884:
1875:
1871:
1835:
1834:
1830:
1816:
1815:
1811:
1777:
1776:
1771:
1770:
1766:
1713:
1712:
1708:
1679:Berthé, Valérie
1676:
1675:
1671:
1648:
1647:
1622:
1621:
1609:
1583:
1582:
1578:
1572:
1557:
1556:
1552:
1523:
1522:
1518:
1512:
1497:
1496:
1492:
1486:
1472:, eds. (2001),
1467:
1466:
1462:
1433:
1432:
1428:
1403:
1402:
1398:
1392:
1375:
1374:
1370:
1321:
1320:
1313:
1288:
1287:
1283:
1277:
1259:
1258:
1254:
1221:
1220:
1213:
1148:
1147:
1140:
1126:
1095:
1094:
1087:
1081:
1062:
1061:
1057:
1052:
1035:
1026:
1020:
1012:
1000:
995:
973:
972:
953:
952:
930:
929:
919:
916:
914:Related results
906:
902:
896:
886:
876:
866:
860:
856:
846:
842:
836:
828:
818:
812:
769:
755:
746:
739:
733:
724:
720:
713:
709:
685:
619:
618:
592:
591:
564:
553:
552:
533:
532:
502:
479:
478:
459:
458:
387:
328:
323:
286:
285:
283:
264:
263:
215:
214:
195:
194:
175:
174:
123:
122:
103:
102:
99:
82:
64:
58:
51:
44:
38:
34:
19:
12:
11:
5:
2646:
2644:
2636:
2635:
2630:
2625:
2615:
2614:
2609:
2608:
2586:
2583:
2580:
2577:
2574:
2570:
2567:
2550:
2524:(4): 525–534,
2503:
2500:
2497:
2494:
2474:
2457:
2431:(3): 264–266,
2410:
2390:(3): 325–326,
2369:
2366:
2344:
2285:
2231:
2182:
2178:
2174:
2171:
2154:
2110:(2): 446–465,
2094:
2038:
2010:(3): 503–552,
1992:
1966:(3): 665–670,
1945:
1942:
1938:
1935:
1931:
1928:
1924:
1921:
1918:
1915:
1912:
1908:
1905:
1902:
1899:
1882:
1869:
1849:(2): 187–189,
1828:
1809:
1787:
1784:
1764:
1724:(2): 537–557,
1706:
1669:
1655:
1635:
1632:
1629:
1607:
1576:
1570:
1550:
1516:
1510:
1490:
1484:
1460:
1448:10.2307/745935
1442:(2): 187–206,
1426:
1396:
1390:
1368:
1311:
1281:
1275:
1252:
1232:(3): 360–370,
1211:
1159:(8): 741–745,
1138:
1124:
1085:
1079:
1054:
1053:
1051:
1048:
1047:
1046:
1041:
1034:
1031:
983:
980:
960:
940:
937:
915:
912:
794:ergodic theory
759:Hugo Steinhaus
754:
751:
693:Fibonacci word
684:
681:
629:
626:
602:
599:
579:
576:
571:
567:
563:
560:
540:
520:
517:
514:
509:
505:
501:
498:
495:
492:
489:
486:
466:
403:perfect fifths
386:
383:
327:
324:
322:
319:
305:
302:
299:
296:
293:
271:
246:
243:
240:
237:
234:
231:
228:
225:
222:
202:
182:
154:
151:
148:
145:
142:
139:
136:
133:
130:
110:
98:
95:
72:Hugo Steinhaus
17:
13:
10:
9:
6:
4:
3:
2:
2645:
2634:
2631:
2629:
2626:
2624:
2621:
2620:
2618:
2604:
2600:
2581:
2578:
2575:
2568:
2565:
2554:
2551:
2547:
2543:
2539:
2535:
2531:
2527:
2523:
2519:
2518:
2501:
2498:
2495:
2492:
2472:
2461:
2458:
2454:
2450:
2446:
2442:
2438:
2434:
2430:
2426:
2425:
2417:
2415:
2411:
2407:
2403:
2398:
2393:
2389:
2385:
2384:
2367:
2364:
2353:
2351:
2349:
2345:
2341:
2337:
2333:
2329:
2325:
2321:
2317:
2313:
2309:
2305:
2304:
2296:
2289:
2286:
2282:
2278:
2274:
2270:
2266:
2262:
2257:
2252:
2248:
2244:
2243:
2235:
2232:
2228:
2224:
2220:
2216:
2212:
2208:
2204:
2200:
2199:
2180:
2172:
2169:
2158:
2155:
2151:
2147:
2143:
2139:
2135:
2131:
2127:
2123:
2118:
2113:
2109:
2105:
2098:
2095:
2091:
2087:
2083:
2079:
2074:
2069:
2064:
2059:
2055:
2051:
2050:
2042:
2039:
2035:
2031:
2027:
2023:
2018:
2013:
2009:
2005:
2004:
1996:
1993:
1989:
1985:
1981:
1977:
1973:
1969:
1965:
1961:
1960:
1940:
1936:
1933:
1929:
1926:
1922:
1919:
1916:
1913:
1903:
1900:
1886:
1883:
1879:
1873:
1870:
1866:
1862:
1857:
1852:
1848:
1844:
1843:
1838:
1832:
1829:
1824:
1820:
1813:
1810:
1805:
1801:
1785:
1782:
1774:
1768:
1765:
1761:
1757:
1753:
1749:
1745:
1741:
1737:
1732:
1727:
1723:
1719:
1718:
1710:
1707:
1702:
1698:
1694:
1690:
1689:
1684:
1680:
1673:
1670:
1653:
1633:
1630:
1627:
1618:
1614:
1610:
1604:
1600:
1597:, Cambridge:
1596:
1595:
1590:
1586:
1580:
1577:
1573:
1571:9781317513421
1567:
1563:
1562:
1554:
1551:
1547:
1543:
1539:
1535:
1531:
1527:
1520:
1517:
1513:
1511:9780198032977
1507:
1503:
1502:
1494:
1491:
1487:
1485:9780198162056
1481:
1477:
1476:
1471:
1464:
1461:
1457:
1453:
1449:
1445:
1441:
1437:
1430:
1427:
1423:
1419:
1415:
1411:
1407:
1400:
1397:
1393:
1391:0-9665201-1-4
1387:
1383:
1379:
1372:
1369:
1365:
1361:
1357:
1353:
1349:
1345:
1340:
1335:
1331:
1327:
1326:
1318:
1316:
1312:
1307:
1302:
1298:
1294:
1293:
1285:
1282:
1278:
1276:9781400832903
1272:
1268:
1267:
1262:
1261:Adam, John A.
1256:
1253:
1249:
1245:
1240:
1235:
1231:
1227:
1226:
1218:
1216:
1212:
1208:
1204:
1200:
1196:
1192:
1188:
1184:
1180:
1176:
1172:
1167:
1162:
1158:
1154:
1153:
1145:
1143:
1139:
1135:
1131:
1127:
1121:
1117:
1113:
1108:
1103:
1099:
1092:
1090:
1086:
1082:
1080:9780521823326
1076:
1072:
1071:
1066:
1059:
1056:
1049:
1045:
1042:
1040:
1037:
1036:
1032:
1030:
1025:that land in
1023:
1018:
1009:
1007:
998:
981:
978:
958:
938:
935:
926:
922:
913:
911:
899:
893:
889:
883:
879:
873:
869:
863:
853:
849:
839:
834:
827:to be an arc
826:
821:
815:
809:
807:
803:
802:Mayero (2000)
799:
795:
791:
787:
783:
779:
773:
768:
767:János Surányi
764:
760:
752:
750:
742:
737:
727:
716:
706:
705:Sturmian word
698:
697:Sturmian word
694:
689:
682:
680:
676:
674:
670:
666:
662:
658:
654:
650:
646:
645:tuning system
641:
627:
624:
616:
600:
597:
577:
574:
569:
565:
561:
558:
538:
515:
512:
507:
503:
499:
496:
493:
487:
484:
464:
456:
455:complex plane
452:
448:
444:
443:perfect fifth
440:
436:
435:musical tones
432:
428:
424:
416:
412:
408:
404:
400:
396:
393:Tones of the
391:
384:
382:
380:
376:
375:Fermat spiral
372:
368:
359:
358:Fermat spiral
354:
350:
348:
344:
337:
332:
325:
320:
318:
303:
300:
297:
294:
291:
269:
260:
259:unit interval
244:
241:
238:
235:
232:
229:
226:
223:
220:
200:
180:
172:
168:
152:
149:
146:
143:
140:
137:
134:
131:
128:
108:
96:
94:
92:
86:
81:
80:János Surányi
77:
73:
68:
61:
55:
48:
41:
32:
28:
24:
16:
2602:
2598:
2553:
2521:
2515:
2460:
2428:
2422:
2387:
2381:
2310:(1): 65–85,
2307:
2301:
2288:
2246:
2240:
2234:
2202:
2196:
2157:
2107:
2103:
2097:
2063:math/0609536
2053:
2047:
2041:
2007:
2001:
1995:
1963:
1957:
1885:
1872:
1846:
1840:
1831:
1822:
1818:
1812:
1803:
1799:
1767:
1759:
1721:
1715:
1709:
1692:
1686:
1672:
1593:
1585:Lothaire, M.
1579:
1560:
1553:
1532:(2): 79–98,
1529:
1525:
1519:
1500:
1493:
1474:
1463:
1439:
1435:
1429:
1405:
1399:
1381:
1371:
1329:
1325:Nonlinearity
1323:
1296:
1290:
1284:
1265:
1255:
1229:
1228:, Series A,
1223:
1156:
1150:
1097:
1069:
1058:
1021:
1010:
996:
924:
920:
917:
897:
891:
887:
881:
877:
871:
867:
861:
851:
847:
837:
832:
824:
819:
813:
810:
756:
740:
725:
714:
702:
677:
642:
615:power of two
433:between two
423:music theory
420:
385:Music theory
367:golden ratio
363:
347:golden angle
340:
336:golden angle
326:Plant growth
321:Applications
193:and integer
100:
69:
59:
53:
46:
39:
30:
26:
22:
20:
15:
2249:: 175–190,
770: [
763:Vera T. Sós
736:-intercepts
451:unit circle
343:phyllotaxis
257:divide the
171:real number
83: [
76:Vera T. Sós
2617:Categories
2485:for which
1773:Sós, V. T.
1731:1707.04094
1617:1001.68093
1339:1904.10815
1299:(2): 333,
1166:1612.04906
1107:cs/0609124
1050:References
796:, and the
411:dodecagram
379:Delone set
2605:: 323–324
2579:
2569:ξ
2546:120454265
2502:ϕ
2493:θ
2453:125810745
2256:0803.1250
2227:121496726
2173:θ
2117:1107.4134
2090:119655772
2034:123011205
1988:123400321
1941:…
1904:ξ
1825:: 107–111
1806:: 127–134
1786:α
1546:120586231
1422:184482714
1364:129945118
1207:119670663
786:geodesics
669:semitones
628:π
601:π
578:ρ
575:
562:π
539:ρ
516:ν
513:
497:π
488:
465:ν
431:frequency
407:semitones
304:α
301:π
292:θ
270:α
245:α
236:…
230:α
221:α
181:α
153:θ
144:…
138:θ
129:θ
97:Statement
2340:55686324
1756:67851217
1681:(1998),
1587:(2002),
1263:(2011),
1033:See also
657:generate
282:and the
2538:0041891
2445:3768035
2406:0548632
2332:3505670
2312:Bibcode
2281:6389675
2273:2443351
2219:0217019
2142:2873022
2122:Bibcode
2082:2419185
2026:2319157
1980:0202668
1865:0104651
1748:4094564
1701:1643286
1344:Bibcode
1248:0957201
1199:3706822
1134:3228597
691:In the
453:in the
2544:
2536:
2451:
2443:
2404:
2338:
2330:
2279:
2271:
2225:
2217:
2148:
2140:
2088:
2080:
2032:
2024:
1986:
1978:
1863:
1754:
1746:
1699:
1615:
1605:
1568:
1544:
1508:
1482:
1456:745935
1454:
1420:
1388:
1362:
1273:
1246:
1205:
1197:
1189:
1132:
1122:
1077:
1022:θ
997:θ
925:θ
898:θ
892:θ
882:θ
872:θ
862:θ
852:θ
838:θ
820:θ
814:θ
776:, and
439:octave
284:angle
89:, and
60:θ
54:θ
47:θ
40:θ
2542:S2CID
2449:S2CID
2336:S2CID
2298:(PDF)
2277:S2CID
2251:arXiv
2223:S2CID
2150:99723
2146:S2CID
2112:arXiv
2086:S2CID
2058:arXiv
2030:S2CID
1984:S2CID
1752:S2CID
1726:arXiv
1542:S2CID
1452:JSTOR
1418:S2CID
1360:S2CID
1334:arXiv
1203:S2CID
1187:JSTOR
1161:arXiv
1130:S2CID
1102:arXiv
1004:is a
833:rigid
774:]
653:piano
87:]
29:, or
2499:<
1603:ISBN
1566:ISBN
1506:ISBN
1480:ISBN
1386:ISBN
1271:ISBN
1120:ISBN
1075:ISBN
425:, a
2597:",
2576:mod
2526:doi
2514:",
2433:doi
2429:125
2392:doi
2320:doi
2308:161
2261:doi
2247:136
2207:doi
2195:",
2177:mod
2130:doi
2108:146
2068:doi
2054:128
2012:doi
1968:doi
1956:",
1851:doi
1798:",
1736:doi
1667:73.
1613:Zbl
1534:doi
1444:doi
1410:doi
1352:doi
1301:doi
1234:doi
1179:hdl
1171:doi
1157:124
1112:doi
825:gap
806:Coq
788:of
743:+ 1
728:+ 1
717:+ 1
566:log
504:log
485:exp
421:In
2619::
2601:,
2540:,
2534:MR
2532:,
2522:46
2520:,
2447:,
2441:MR
2439:,
2427:,
2413:^
2402:MR
2400:,
2388:28
2386:,
2347:^
2334:,
2328:MR
2326:,
2318:,
2306:,
2300:,
2275:,
2269:MR
2267:,
2259:,
2245:,
2221:,
2215:MR
2213:,
2203:63
2201:,
2144:,
2138:MR
2136:,
2128:,
2120:,
2106:,
2084:,
2078:MR
2076:,
2066:,
2052:,
2028:,
2022:MR
2020:,
2008:59
2006:,
1982:,
1976:MR
1974:,
1964:61
1962:,
1861:MR
1859:,
1847:46
1845:,
1821:,
1802:,
1758:,
1750:,
1744:MR
1742:,
1734:,
1722:53
1720:,
1697:MR
1693:44
1691:,
1685:,
1611:,
1591:,
1540:,
1528:,
1450:,
1440:11
1438:,
1416:,
1358:,
1350:,
1342:,
1330:33
1328:,
1314:^
1297:36
1295:,
1244:MR
1242:,
1230:45
1214:^
1201:,
1195:MR
1193:,
1185:,
1177:,
1169:,
1155:,
1141:^
1128:,
1118:,
1110:,
1088:^
1008:.
999:/2
923:+
890:+
880:+
870:+
850:+
800:.
792:,
772:hu
765:,
703:A
675:.
643:A
85:hu
78:,
50:,
43:,
25:,
2603:2
2585:)
2582:1
2573:(
2566:n
2528::
2496:N
2473:N
2435::
2394::
2368:d
2365:3
2322::
2314::
2263::
2253::
2209::
2181:1
2170:n
2132::
2124::
2114::
2070::
2060::
2014::
1970::
1944:)
1937:,
1934:2
1930:,
1927:1
1923:,
1920:0
1917:=
1914:n
1911:(
1907:}
1901:n
1898:{
1853::
1823:1
1804:1
1783:n
1738::
1728::
1654:d
1634:1
1631:+
1628:d
1536::
1530:1
1446::
1412::
1354::
1346::
1336::
1303::
1236::
1181::
1173::
1163::
1114::
1104::
1027:A
1013:A
1001:π
982:d
979:3
959:d
939:d
936:3
921:A
907:A
903:A
888:A
878:A
868:A
857:A
848:A
843:A
829:A
747:n
741:n
734:y
726:n
721:n
715:n
710:n
625:2
598:2
570:2
559:2
519:)
508:2
500:i
494:2
491:(
417:.
316:.
298:2
295:=
242:n
239:,
233:,
227:2
224:,
201:n
150:n
147:,
141:,
135:2
132:,
109:n
65:π
52:3
45:2
35:n
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.