1925:
5510:
4234:(twice continuously differentiable) embedding of a flat torus into 3-space. (The idea of the proof is to take a large sphere containing such a flat torus in its interior, and shrink the radius of the sphere until it just touches the torus for the first time. Such a point of contact must be a tangency. But that would imply that part of the torus, since it has zero curvature everywhere, must lie strictly outside the sphere, which is a contradiction.) On the other hand, according to the
5257:
4349:, yielding a so-called "smooth fractal". The key to obtain the smoothness of this corrugated torus is to have the amplitudes of successive corrugations decreasing faster than their "wavelengths". (These infinitely recursive corrugations are used only for embedding into three dimensions; they are not an intrinsic feature of the flat torus.) This is the first time that any such embedding was defined by explicit equations or depicted by computer graphics.
4246:
4544:
4533:
415:
3152:
4639:
392:
369:
3391:
1865:
4568:
40:
437:
64:
3367:
636:
1573:
4946:
48:
5120:
1488:
4467:
two-tori. (And so the torus itself is the surface of genus 1.) To form a connected sum of two surfaces, remove from each the interior of a disk and "glue" the surfaces together along the boundary circles. (That is, merge the two boundary circles so they become just one circle.) To form the connected
3632:
everywhere. It is flat in the same sense that the surface of a cylinder is flat. In 3 dimensions, one can bend a flat sheet of paper into a cylinder without stretching the paper, but this cylinder cannot be bent into a torus without stretching the paper (unless some regularity and differentiability
2402:
that circles the torus' "hole" (say, a circle that traces out a particular latitude) and then circles the torus' "body" (say, a circle that traces out a particular longitude) can be deformed to a path that circles the body and then the hole. So, strictly 'latitudinal' and strictly 'longitudinal'
2406:
If a torus is punctured and turned inside out then another torus results, with lines of latitude and longitude interchanged. This is equivalent to building a torus from a cylinder, by joining the circular ends together, in two ways: around the outside like joining two ends of a garden hose, or
3346:
whose top and bottom faces are connected with a 1/3 twist (120°): the 3-dimensional interior corresponds to the points on the 3-torus where all 3 coordinates are distinct, the 2-dimensional face corresponds to points with 2 coordinates equal and the 3rd different, while the 1-dimensional edge
451:
2393:
1503:, obtained from cutting the tube along the plane of a small circle, and unrolling it by straightening out (rectifying) the line running around the center of the tube. The losses in surface area and volume on the inner side of the tube exactly cancel out the gains on the outer side.
5237:
5467:
4173:
1860:{\displaystyle {\begin{aligned}A&=4\pi ^{2}\left({\frac {p+q}{2}}\right)\left({\frac {p-q}{2}}\right)=\pi ^{2}(p+q)(p-q),\\V&=2\pi ^{2}\left({\frac {p+q}{2}}\right)\left({\frac {p-q}{2}}\right)^{2}={\tfrac {1}{4}}\pi ^{2}(p+q)(p-q)^{2}.\end{aligned}}}
1307:
4813:
4962:, 1), its homotopy equivalences, up to homotopy, can be identified with automorphisms of the fundamental group); all homotopy equivalences of the torus can be realized by homeomorphisms – every homotopy equivalence is homotopic to a homeomorphism.
5004:
2601:
4420:
to a) the square torus (total angle = π) and b) the hexagonal torus (total angle = 2π/3). These are the only conformal equivalence classes of flat tori that have any conformal automorphisms other than those generated by translations and negation.
2462:
2407:
through the inside like rolling a sock (with the toe cut off). Additionally, if the cylinder was made by gluing two opposite sides of a rectangle together, choosing the other two sides instead will cause the same reversal of orientation.
1068:
1278:
910:
330:
An example of a torus can be constructed by taking a rectangular strip of flexible material such as rubber, and joining the top edge to the bottom edge, and the left edge to the right edge, without any half-twists (compare
4408:
along their (identical) boundaries, where each triangle has angles of π/2, π/3, and 0. As a result the area of each triangle can be calculated as π - (π/2 + π/3 + 0) = π/6, so it follows that the compactified moduli space
5225:, the upper bound is tight.) Equivalently, in a torus divided into regions, it is always possible to color the regions using no more than seven colors so that no neighboring regions are the same color. (Contrast with the
3930:
2272:
1578:
1312:
631:{\displaystyle {\begin{aligned}x(\theta ,\varphi )&=(R+r\cos \theta )\cos {\varphi }\\y(\theta ,\varphi )&=(R+r\cos \theta )\sin {\varphi }\\z(\theta ,\varphi )&=r\sin \theta \\\end{aligned}}}
4361:, one says that any two smooth compact geometric surfaces are "conformally equivalent" when there exists a smooth homeomorphism between them that is both angle-preserving and orientation-preserving. The
4391:
by adding one additional point that represents the limiting case as a rectangular torus approaches an aspect ratio of 0 in the limit. The result is that this compactified moduli space is a sphere with
3747:
3256:
5326:
4724:
4381:
may be identified with a punctured sphere that is smooth except for two points that have less angle than 2π (radians) around them: One has total angle = π and the other has total angle = 2π/3.
456:
4019:
3591:
3309:
2648:
2228:
5752:
1900:, and is known as the "poloidal" direction. These terms were first used in a discussion of the Earth's magnetic field, where "poloidal" was used to denote "the direction toward the poles".
688:
3370:
In three dimensions, one can bend a rectangle into a torus, but doing this necessarily affects the distances measured along the surface, as seen by the distortion of the checkered pattern.
4941:{\displaystyle \operatorname {MCG} _{\operatorname {Ho} }(\mathbb {T} ^{n})=\operatorname {Aut} (\pi _{1}(X))=\operatorname {Aut} (\mathbb {Z} ^{n})=\operatorname {GL} (n,\mathbb {Z} ).}
5223:
6349:
5115:{\displaystyle 1\to \operatorname {Homeo} _{0}(\mathbb {T} ^{n})\to \operatorname {Homeo} (\mathbb {T} ^{n})\to \operatorname {MCG} _{\operatorname {TOP} }(\mathbb {T} ^{n})\to 1.}
925:
5177:
2522:
271:
4996:
4782:
4753:
4339:
4302:
4221:
3544:
3506:
3477:
3440:
3104:
3060:
2967:
2927:
2808:
2772:
2739:
2710:
2677:
2126:
2088:
1182:
811:
5256:
3628:
This metric of the square flat torus can also be realised by specific embeddings of the familiar 2-torus into
Euclidean 4-space or higher dimensions. Its surface has zero
1483:{\displaystyle {\begin{aligned}A&=\left(2\pi r\right)\left(2\pi R\right)=4\pi ^{2}Rr,\\V&=\left(\pi r^{2}\right)\left(2\pi R\right)=2\pi ^{2}Rr^{2}.\end{aligned}}}
4396:
points each having less than 2π total angle around them. (Such points are termed "cusps".) This additional point will have zero total angle around it. Due to symmetry,
1954:
6098:
4345:
as it is constructed by repeatedly corrugating an ordinary torus. Like fractals, it has no defined
Gaussian curvature. However, unlike fractals, it does have defined
4273:
306:
5871:
765:
2251:
802:
734:
711:
107:
with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a
6017:
273:, and the latter is taken to be the definition in that context. It is a compact 2-manifold of genus 1. The ring torus is one way to embed this space into
6342:
3125:
5494:
5240:
This construction shows the torus divided into seven regions, every one of which touches every other, meaning each must be assigned a unique color.
3375:
2442:
on the 2-torus can be represented as a two-sheeted cover of the 2-sphere. The points on the torus corresponding to the ramification points are the
6129:
4468:
sum of more than two surfaces, successively take the connected sum of two of them at a time until they are all connected. In this sense, a genus
5678:, Author: Kozak Ana Maria, Pompeya Pastorelli Sonia, Verdanega Pedro Emilio, Editorial: McGraw-Hill, Edition 2007, 744 pages, language: Spanish
323:, a torus is any topological space that is homeomorphic to a torus. The surface of a coffee cup and a doughnut are both topological tori with
6335:
5770:
5715:
5675:
4377:" of the torus to contain one point for each conformal equivalence class, with the appropriate topology. It turns out that this moduli space
6288:
6177:
4341:
was found. It is a flat torus in the sense that, as a metric space, it is isometric to a flat square torus. It is similar in structure to a
3801:
2388:{\displaystyle \pi _{1}(\mathbb {T} ^{2})=\pi _{1}(\mathbb {S} ^{1})\times \pi _{1}(\mathbb {S} ^{1})\cong \mathbb {Z} \times \mathbb {Z} .}
5798:
5300:
exactly once. It is a torus because the edges are considered wraparound for the purpose of finding matrices. Its name comes from the
6035:
5707:
5692:
2403:
paths commute. An equivalent statement may be imagined as two shoelaces passing through each other, then unwinding, then rewinding.
1976:
3642:
4795:, the mapping class group can be identified as the action on the first homology (or equivalently, first cohomology, or on the
67:
A ring torus with aspect ratio 3, the ratio between the diameters of the larger (magenta) circle and the smaller (red) circle.
51:
As the distance from the axis of revolution decreases, the ring torus becomes a horn torus, then a spindle torus, and finally
3204:
6058:
5462:{\displaystyle {\begin{pmatrix}n+2\\n-1\end{pmatrix}}+{\begin{pmatrix}n\\n-1\end{pmatrix}}={\tfrac {1}{6}}(n^{3}+3n^{2}+8n)}
3405:
with 1 vertex, 2 orthogonal edges, and one square face. It is seen here stereographically projected into 3-space as a torus.
4168:{\displaystyle T=\left\{(x,y,z,w)\in \mathbb {S} ^{3}\mid x^{2}+y^{2}={\frac {1}{2}},\ z^{2}+w^{2}={\frac {1}{2}}\right\}.}
6039:
5579:
5564:
3194:
1892:
measures the same angle as it does in the spherical system, but is known as the "toroidal" direction. The center point of
152:). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered
4689:
3636:
A simple 4-dimensional
Euclidean embedding of a rectangular flat torus (more general than the square one) is as follows:
5273:
with 1s as panels and 0s as holes in the mesh – with consistent orientation, every 3×3 matrix appears exactly once
1301:
4952:
3550:
3268:
2609:
1937:
6488:
5918:
Padgett, Adele (2014). "FUNDAMENTAL GROUPS: MOTIVATION, COMPUTATION METHODS, AND APPLICATIONS" REA Program, Uchicago.
4491:
while a genus one surface (without boundary) is the ordinary torus. The surfaces of higher genus are sometimes called
2149:
1908:
1870:
1947:
1941:
1933:
5824:
4521:
surface is topologically equivalent to either the sphere or the connect sum of some number of tori, disks, and real
643:
4242:
embedding exists. This is solely an existence proof and does not provide explicit equations for such an embedding.
3795:-space requires one to stretch it, in which case it looks like a regular torus. For example, in the following map:
3395:
2775:
2037:
by a family of nested tori in this manner (with two degenerate circles), a fact which is important in the study of
3410:
2136:
690:
representing rotation around the tube and rotation around the torus' axis of revolution, respectively, where the
5958:
5182:
1958:
6524:
5639:
3379:
3354:
in the work of Dmitri
Tymoczko and collaborators (Felipe Posada, Michael Kolinas, et al.), being used to model
2263:
2096:
2013:
52:
6151:
2095:
to a topological torus as long as it does not intersect its own axis. A particular homeomorphism is given by
6597:
6528:
4628:
100:
47:
20:
5125:
The mapping class group of higher genus surfaces is much more complicated, and an area of active research.
3625:. This particular flat torus (and any uniformly scaled version of it) is known as the "square" flat torus.
2855:
with multiplication). Group multiplication on the torus is then defined by coordinate-wise multiplication.
6327:
5983:
4792:
4511:
4362:
4235:
3165:
2596:{\displaystyle \mathbb {T} ^{n}=\underbrace {\mathbb {S} ^{1}\times \cdots \times \mathbb {S} ^{1}} _{n}.}
313:
31:
6464:
6406:
5634:
5594:
4002:
2061:
1904:
781:
92:
5509:
5151:
2940:
with an integral inverse; these are just the integral matrices with determinant ±1. Making them act on
2250:
236:
6121:
4972:
4758:
4729:
4315:
4278:
4197:
3520:
3482:
3453:
3416:
3080:
3036:
2943:
2903:
2784:
2748:
2715:
2686:
2653:
2102:
2064:
6586:
6561:
5975:
5569:
5297:
5286:
4966:
4726:
of invertible integer matrices, which can be realized as linear maps on the universal covering space
4590:
3335:
3075:
3015:
3008:
5988:
6556:
6550:
5230:
4683:
4675:
4572:
4562:
4448:
4006:
3509:
3124:
3114:
2439:
2238:
1177:
445:
324:
5898:
6451:
6284:
6181:
6009:
5654:
5609:
5539:
5515:
5301:
5226:
4679:
4444:
4370:
3629:
3512:, as well as the structure of an abelian Lie group. Perhaps the simplest example of this is when
2985:
2435:
119:
6293:
5794:
5919:
6622:
6430:
6313:
6278:
6230:
6090:
6001:
5966:
5847:
5766:
5711:
5703:
5688:
5671:
5472:
parts. (This assumes the pieces may not be rearranged but must remain in place for all cuts.)
5261:
4796:
4401:
4346:
3788:
3769:
2977:
2933:
2930:
2859:
2443:
2259:
2057:
1285:
1063:{\displaystyle \left(x^{2}+y^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\left(x^{2}+y^{2}\right).}
777:
6412:
6272:
6080:
6070:
5993:
5758:
5142:
4800:
4522:
4405:
4312:(continuously differentiable) embedding of a flat torus into 3-dimensional Euclidean space
4245:
3374:
3343:
3067:
2419:
1997:
1126:
1120:
919:
226:
140:
5780:
4543:
4532:
4251:
284:
6514:
6043:
5776:
5529:
5250:
4518:
4434:
4358:
3773:
3594:
3312:
3027:
2779:
2399:
2140:
1888:
As a torus has, effectively, two center points, the centerpoints of the angles are moved;
1289:
1072:
The three classes of standard tori correspond to the three possible aspect ratios between
805:
274:
187:
6476:
3327:
3144:
1273:{\displaystyle {\textstyle {\bigl (}{\sqrt {x^{2}+y^{2}}}-R{\bigr )}^{2}}+z^{2}<r^{2}}
742:
5979:
3330:, the edge corresponding to the orbifold points where the two coordinates coincide. For
6085:
5604:
5589:
5559:
5544:
5534:
5236:
5146:
5138:
5134:
3761:
3151:
2997:
2886:, which (like tori) are compact connected abelian groups, which are not required to be
2852:
2466:
2411:
2026:
1993:
1281:
905:{\displaystyle {\textstyle {\bigl (}{\sqrt {x^{2}+y^{2}}}-R{\bigr )}^{2}}+z^{2}=r^{2}.}
787:
719:
696:
414:
309:
5682:
4638:
773:
of the torus. The typical doughnut confectionery has an aspect ratio of about 3 to 2.
6616:
6577:
6533:
6519:
6417:
5649:
5624:
5619:
5584:
5554:
5549:
5278:
4969:
of the mapping class group splits (an identification of the torus as the quotient of
4579:
4515:
4460:
4373:. In the case of a torus, the constant curvature must be zero. Then one defines the "
4366:
3355:
2867:
2841:
2834:
2423:
222:
174:
5721:
3366:
6424:
6261:
6013:
5744:
5574:
4686:(the connected components of the homeomorphism group) is surjective onto the group
4548:
4537:
4504:
4500:
4374:
3390:
2893:
2092:
2042:
1297:
769:
391:
368:
332:
6233:
3128:
The configuration space of 2 not necessarily distinct points on the circle is the
1873:
is sometimes used. In traditional spherical coordinates there are three measures,
1510:
of an outermost point on the surface of the torus to the center, and the distance
6204:
3983:. In particular, for certain very specific choices of a square flat torus in the
3409:
A flat torus is a torus with the metric inherited from its representation as the
6304:
6122:"Mathematicians Produce First-Ever Image of Flat Torus in 3D | Mathematics"
3402:
2848:
2447:
2415:
2234:
2050:
915:
182:
104:
27:
4627:
The term "toroidal polyhedron" is also used for higher-genus polyhedra and for
3172:
segment of the right edge of the repeated parallelogram is identified with the
713:
is the distance from the center of the tube to the center of the torus and the
6297:
6266:
5762:
5644:
5614:
5505:
4804:
4586:
4567:
3339:
170:
138:. If the axis of revolution passes twice through the circle, the surface is a
39:
6257:
4784:(this corresponds to integer coefficients) and thus descend to the quotient.
4589:
with the topological type of a torus are called toroidal polyhedra, and have
6592:
6481:
6238:
6152:"Mathematics: first-ever image of a flat torus in 3D – CNRS Web site – CNRS"
6075:
5997:
5855:
5748:
2844:
2819:
2461:
2034:
436:
278:
166:
6094:
6005:
5932:
5850:
3334:= 3 this quotient may be described as a solid torus with cross-section an
190:, rather than a circle, around an axis. A solid torus is a torus plus the
63:
6469:
5820:
4788:
4005:
solid tori subsets with the aforesaid flat torus surface as their common
3984:
3980:
3765:
3351:
3263:
3129:
2887:
2883:
2871:
2837:
2019:
1989:
1106:
corresponds to the horn torus, which in effect is a torus with no "hole".
320:
218:
207:
203:
72:
122:
does not touch the circle, the surface has a ring shape and is called a
5524:
4342:
3157:
131:
4182:
having this partitioning property include the square tori of the form
3925:{\displaystyle (x,y,z)=((R+P\sin v)\cos u,(R+P\sin v)\sin u,P\cos v).}
3201:
ordered, not necessarily distinct points on the circle. Symbolically,
2874:
which is a torus of the largest possible dimension. Such maximal tori
344:
308:
in the plane with itself. This produces a geometric object called the
6377:
5629:
5599:
5289:
of symbols from an alphabet (often just 0 and 1) that contains every
4488:
4477:
2508:.) Recalling that the torus is the product space of two circles, the
2001:
1293:
230:
199:
191:
158:
153:
96:
56:
2810:(with the action being taken as vector addition). Equivalently, the
1869:
As a torus is the product of two circles, a modified version of the
1118:
describes the self-intersecting spindle torus; its inner shell is a
26:
This article is about the mathematical surface. For the volume, see
6155:
5235:
4566:
4244:
3389:
3373:
3365:
3150:
3123:
2460:
2249:
440:
Poloidal direction (red arrow) and toroidal direction (blue arrow)
435:
348:
is a Latin word for "a round, swelling, elevation, protuberance".
211:
165:
Real-world objects that approximate a torus of revolution include
62:
46:
38:
156:. If the revolved curve is not a circle, the surface is called a
4678:(or the subgroup of diffeomorphisms) of the torus is studied in
2862:. This is due in part to the fact that in any compact Lie group
2446:. In fact, the conformal type of the torus is determined by the
6331:
3386:
can be projected into 3-dimensions and rotated on a fixed axis.
4633:
2851:
is a compact abelian Lie group (when identified with the unit
2025:
of radius √2. This topological torus is also often called the
1918:
5757:. Geometry and Computing. Vol. 9. Springer, Heidelberg.
1877:, the distance from the center of the coordinate system, and
1094:, the surface will be the familiar ring torus or anchor ring.
277:, but another way to do this is the Cartesian product of the
5920:
https://math.uchicago.edu/~may/REU2014/REUPapers/Padgett.pdf
4487:
As examples, a genus zero surface (without boundary) is the
2469:
in four dimensions performing a simple rotation through the
5489:
3943:
in the above flat torus parametrization form a unit vector
3760:
are positive constants determining the aspect ratio. It is
3742:{\displaystyle (x,y,z,w)=(R\cos u,R\sin u,P\cos v,P\sin v)}
1506:
Expressing the surface area and the volume by the distance
5754:
5487:
1, 2, 6, 13, 24, 40, 62, 91, 128, 174, 230, ... (sequence
2496:
for short. (This is the more typical meaning of the term "
5899:"Applications of the Clifford torus to material textures"
5483:= 0, not covered by the above formulas), are as follows:
4604:= 0. For any number of holes, the formula generalizes to
4416:
The other two cusps occur at the points corresponding in
2900:
are easily constructed from automorphisms of the lattice
2477:
The torus has a generalization to higher dimensions, the
6059:"Doc Madhattan: A flat torus in three dimensional space"
4799:, as these are all naturally isomorphic; also the first
3347:
corresponds to points with all 3 coordinates identical.
2858:
Toroidal groups play an important part in the theory of
1492:
These formulas are the same as for a cylinder of length
194:
inside the torus. Real-world objects that approximate a
6358:
Compact topological surfaces and their immersions in 3D
4650:
3251:{\displaystyle \mathbb {T} ^{n}=(\mathbb {S} ^{1})^{n}}
2878:
have a controlling role to play in theory of connected
2237:
by pasting the opposite edges together, described as a
43:
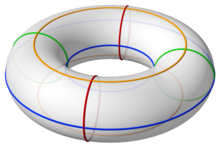
A ring torus with a selection of circles on its surface
6269:
Fly-through cross-sections of a four-dimensional torus
5407:
5376:
5335:
4001:
above, the torus will partition the 3-sphere into two
2741:
under integral shifts in any coordinate. That is, the
1792:
1187:
816:
5329:
5185:
5154:
5007:
4975:
4816:
4761:
4732:
4692:
4400:
may be constructed by glueing together two congruent
4318:
4281:
4254:
4200:
4022:
3804:
3645:
3553:
3523:
3485:
3456:
3419:
3271:
3262:, not necessarily distinct points is accordingly the
3207:
3083:
3039:
2946:
2906:
2787:
2751:
2718:
2689:
2656:
2650:. The torus discussed above is the standard 2-torus,
2612:
2525:
2275:
2152:
2105:
2067:
1576:
1310:
1185:
928:
814:
790:
745:
722:
699:
646:
454:
287:
239:
2266:
of the fundamental group of the circle with itself:
6570:
6542:
6507:
6498:
6444:
6399:
6370:
6363:
6180:. Math.univ-lyon1.fr. 18 April 2012. Archived from
4998:gives a splitting, via the linear maps, as above):
4719:{\displaystyle \operatorname {GL} (n,\mathbb {Z} )}
5724:Encyclopédie des Formes Mathématiques Remarquables
5461:
5217:
5171:
5114:
4990:
4940:
4776:
4747:
4718:
4333:
4296:
4267:
4215:
4167:
3924:
3741:
3585:
3538:
3500:
3471:
3434:
3303:
3250:
3098:
3054:
2961:
2921:
2802:
2766:
2733:
2704:
2671:
2642:
2595:
2434:The 2-torus double-covers the 2-sphere, with four
2387:
2222:
2120:
2082:
1859:
1482:
1272:
1062:
904:
796:
759:
728:
705:
682:
630:
300:
265:
6275:Visualizing high dimensional data with flat torus
3586:{\displaystyle \mathbb {R} ^{2}/\mathbb {Z} ^{2}}
3304:{\displaystyle \mathbb {T} ^{n}/\mathbb {S} _{n}}
2643:{\displaystyle \mathbb {T} ^{1}=\mathbb {S} ^{1}}
5668:Nociones de Geometría Analítica y Álgebra Lineal
4447:there is a more general family of objects, the "
2223:{\displaystyle (x,y)\sim (x+1,y)\sim (x,y+1),\,}
1946:but its sources remain unclear because it lacks
6063:Proceedings of the National Academy of Sciences
5304:, which can be considered a special case where
4238:, which was proven in the 1950s, an isometric
683:{\displaystyle \theta ,\varphi \in [0,2\pi ),}
6343:
3508:. This gives the quotient the structure of a
1514:of an innermost point to the center (so that
1231:
1190:
1156:, the torus degenerates to the circle radius
1140:, the torus degenerates to the sphere radius
860:
819:
8:
4476:doughnuts stuck together side by side, or a
3311:, which is the quotient of the torus by the
2418:to the fundamental group (this follows from
6298:"Topology of a Twisted Torus – Numberphile"
6504:
6367:
6350:
6336:
6328:
5316:A solid torus of revolution can be cut by
5218:{\displaystyle \chi ({\mathsf {K_{7}}})=7}
5137:is seven, meaning every graph that can be
103:one full revolution about an axis that is
6205:"The Tortuous Geometry of the Flat Torus"
6084:
6074:
5987:
5441:
5425:
5406:
5371:
5330:
5328:
5198:
5193:
5192:
5184:
5161:
5156:
5155:
5153:
5097:
5093:
5092:
5079:
5063:
5059:
5058:
5036:
5032:
5031:
5018:
5006:
4982:
4978:
4977:
4974:
4928:
4927:
4900:
4896:
4895:
4864:
4839:
4835:
4834:
4821:
4815:
4768:
4764:
4763:
4760:
4739:
4735:
4734:
4731:
4709:
4708:
4691:
4365:guarantees that every Riemann surface is
4325:
4321:
4320:
4317:
4288:
4284:
4283:
4280:
4259:
4253:
4207:
4203:
4202:
4199:
4147:
4138:
4125:
4105:
4096:
4083:
4070:
4066:
4065:
4021:
3803:
3644:
3577:
3573:
3572:
3566:
3560:
3556:
3555:
3552:
3530:
3526:
3525:
3522:
3492:
3488:
3487:
3484:
3463:
3459:
3458:
3455:
3426:
3422:
3421:
3418:
3295:
3291:
3290:
3284:
3278:
3274:
3273:
3270:
3242:
3232:
3228:
3227:
3214:
3210:
3209:
3206:
3161:is an example of a torus in music theory.
3090:
3086:
3085:
3082:
3046:
3042:
3041:
3038:
2953:
2949:
2948:
2945:
2913:
2909:
2908:
2905:
2829:-torus in this sense is an example of an
2794:
2790:
2789:
2786:
2758:
2754:
2753:
2750:
2725:
2721:
2720:
2717:
2696:
2692:
2691:
2688:
2663:
2659:
2658:
2655:
2634:
2630:
2629:
2619:
2615:
2614:
2611:
2606:The standard 1-torus is just the circle:
2584:
2572:
2568:
2567:
2551:
2547:
2546:
2542:
2532:
2528:
2527:
2524:
2378:
2377:
2370:
2369:
2357:
2353:
2352:
2342:
2326:
2322:
2321:
2311:
2295:
2291:
2290:
2280:
2274:
2233:or, equivalently, as the quotient of the
2219:
2151:
2112:
2108:
2107:
2104:
2074:
2070:
2069:
2066:
1977:Learn how and when to remove this message
1885:, angles measured from the center point.
1844:
1807:
1791:
1782:
1760:
1733:
1723:
1663:
1634:
1608:
1598:
1577:
1575:
1467:
1454:
1414:
1373:
1311:
1309:
1264:
1251:
1236:
1230:
1229:
1214:
1201:
1195:
1189:
1188:
1186:
1184:
1046:
1033:
1018:
1002:
991:
978:
965:
952:
939:
927:
893:
880:
865:
859:
858:
843:
830:
824:
818:
817:
815:
813:
789:
784:for a torus radially symmetric about the
749:
744:
721:
698:
645:
578:
514:
455:
453:
292:
286:
257:
244:
238:
5254:
4527:
3319:letters (by permuting the coordinates).
2398:Intuitively speaking, this means that a
6057:Filippelli, Gianluigi (27 April 2012).
5736:
5475:The first 11 numbers of parts, for 0 ≤
4275:isometric embedding of a flat torus in
3394:The simplest tiling of a flat torus is
3350:These orbifolds have found significant
3004:-torus is a free abelian group of rank
2822:by gluing the opposite faces together.
2056:The surface described above, given the
1300:of its torus are easily computed using
5199:
5195:
5162:
5158:
4194:is a rotation of 4-dimensional space
3106:whose generators are the duals of the
2969:in the usual way, one has the typical
2847:. This follows from the fact that the
180:A torus should not be confused with a
5827:from the original on 13 December 2014
4353:Conformal classification of flat tori
3979:/2 parameterize the unit 3-sphere as
3633:conditions are given up, see below).
3593:, which can also be described as the
3164:The Tonnetz is only truly a torus if
2840:. It is also an example of a compact
2512:-dimensional torus is the product of
2135:The torus can also be described as a
16:Doughnut-shaped surface of revolution
7:
5687:. Cambridge University Press, 2002.
4227:is a member of the Lie group SO(4).
2254:Turning a punctured torus inside-out
6312:Anders Sandberg (4 February 2014).
4755:that preserve the standard lattice
4387:may be turned into a compact space
80:
6279:Polydoes, doughnut-shaped polygons
6120:Enrico de Lazaro (18 April 2012).
6023:from the original on 25 July 2011.
5906:Journal of Applied Crystallography
5801:from the original on 29 April 2012
5795:"Equations for the Standard Torus"
5698:V. V. Nikulin, I. R. Shafarevich.
5179:can be embedded on the torus, and
3401:, constructed on the surface of a
2882:. Toroidal groups are examples of
2712:can be described as a quotient of
2679:. And similar to the 2-torus, the
1907:are more commonly used to discuss
14:
6101:from the original on 25 June 2012
5172:{\displaystyle {\mathsf {K_{7}}}}
4472:surface resembles the surface of
4230:It is known that there exists no
3189:-fold product of the circle, the
2012:. This can be viewed as lying in
429:: self-intersecting spindle torus
266:{\displaystyle S^{1}\times S^{1}}
6132:from the original on 1 June 2012
5959:"The Geometry of Musical Chords"
5957:Tymoczko, Dmitri (7 July 2006).
5876:Oxford English Dictionary Online
5508:
4991:{\displaystyle \mathbb {R} ^{n}}
4777:{\displaystyle \mathbb {Z} ^{n}}
4748:{\displaystyle \mathbb {R} ^{n}}
4637:
4542:
4531:
4334:{\displaystyle \mathbb {R} ^{3}}
4297:{\displaystyle \mathbb {R} ^{3}}
4216:{\displaystyle \mathbb {R} ^{4}}
3539:{\displaystyle \mathbb {Z} ^{2}}
3501:{\displaystyle \mathbb {Z} ^{2}}
3472:{\displaystyle \mathbb {R} ^{2}}
3435:{\displaystyle \mathbb {R} ^{2}}
3099:{\displaystyle \mathbb {Z} ^{n}}
3055:{\displaystyle \mathbb {T} ^{n}}
2962:{\displaystyle \mathbb {R} ^{n}}
2922:{\displaystyle \mathbb {Z} ^{n}}
2803:{\displaystyle \mathbb {Z} ^{n}}
2767:{\displaystyle \mathbb {R} ^{n}}
2734:{\displaystyle \mathbb {R} ^{n}}
2705:{\displaystyle \mathbb {T} ^{n}}
2672:{\displaystyle \mathbb {T} ^{2}}
2500:-torus", the other referring to
2465:A stereographic projection of a
2121:{\displaystyle \mathbb {R} ^{3}}
2083:{\displaystyle \mathbb {R} ^{3}}
1923:
1284:(and, hence, homeomorphic) to a
413:
390:
367:
186:, which is formed by rotating a
134:to the circle, the surface is a
6178:"Flat tori finally visualized!"
6034:Phillips, Tony (October 2006).
5897:De Graef, Marc (7 March 2024).
5722:"Tore (notion géométrique)" at
4514:for surfaces states that every
2422:since the fundamental group is
130:. If the axis of revolution is
5797:. Geom.uiuc.edu. 6 July 1995.
5456:
5418:
5206:
5189:
5106:
5103:
5088:
5072:
5069:
5054:
5045:
5042:
5027:
5011:
4932:
4918:
4906:
4891:
4879:
4876:
4870:
4857:
4845:
4830:
4713:
4699:
4058:
4034:
3916:
3889:
3868:
3853:
3832:
3829:
3823:
3805:
3736:
3676:
3670:
3646:
3239:
3223:
2363:
2348:
2332:
2317:
2301:
2286:
2213:
2195:
2189:
2171:
2165:
2153:
1841:
1828:
1825:
1813:
1696:
1684:
1681:
1669:
914:Algebraically eliminating the
674:
659:
602:
590:
569:
548:
538:
526:
505:
484:
474:
462:
1:
6040:American Mathematical Society
5565:Irrational winding of a torus
5320:(> 0) planes into at most
5145:of at most seven. (Since the
3258:. The configuration space of
3066:) can be identified with the
6273:"Relational Perspective Map"
5479:≤ 10 (including the case of
4529:
4507:are also occasionally used.
3352:applications to music theory
2814:-torus is obtained from the
2099:the topological torus into
2097:stereographically projecting
1296:of this solid torus and the
6036:"Take on Math in the Media"
5308:is 1 (one dimension).
4308:In April 2012, an explicit
4009:. One example is the torus
3764:to a regular torus but not
1909:magnetic confinement fusion
1871:spherical coordinate system
736:is the radius of the tube.
383:: ring torus or anchor ring
6641:
5580:Loewner's torus inequality
5248:
4560:
4432:
3787:) into Euclidean 3-space.
3597:under the identifications
3450:is a discrete subgroup of
3112:
2929:, which are classified by
2143:under the identifications
1896:is moved to the center of
1124:and its outer shell is an
640:using angular coordinates
25:
18:
6203:Hoang, Lê Nguyên (2016).
5878:. Oxford University Press
5763:10.1007/978-3-642-34364-3
5264:model of de Bruijn torus
4495:-holed tori (or, rarely,
4369:to one that has constant
3326:= 2, the quotient is the
3176:segment of the left edge.
3132:quotient of the 2-torus,
2262:of the torus is just the
1302:Pappus's centroid theorem
162:, as in a square toroid.
95:generated by revolving a
5640:Torus-based cryptography
4624:is the number of holes.
3380:stereographic projection
3168:is assumed, so that the
1932:This section includes a
19:Not to be confused with
6489:Sphere with three holes
6076:10.1073/pnas.1118478109
5998:10.1126/science.1126287
4953:Eilenberg–MacLane space
4631:of toroidal polyhedra.
4499:-fold tori). The terms
4413:has area equal to π/3.
2128:from the north pole of
2018:and is a subset of the
1961:more precise citations.
361:vertical cross-sections
150:self-intersecting torus
101:three-dimensional space
5463:
5274:
5241:
5219:
5173:
5116:
4992:
4951:Since the torus is an
4942:
4778:
4749:
4720:
4583:
4512:classification theorem
4367:conformally equivalent
4363:Uniformization theorem
4335:
4305:
4298:
4269:
4217:
4169:
3926:
3743:
3587:
3540:
3502:
3473:
3436:
3406:
3387:
3371:
3305:
3252:
3178:
3166:enharmonic equivalence
3148:
3100:
3056:
3014:. It follows that the
2963:
2923:
2866:one can always find a
2804:
2768:
2735:
2706:
2673:
2644:
2597:
2474:
2389:
2255:
2224:
2122:
2084:
1861:
1484:
1274:
1064:
906:
798:
761:
730:
707:
684:
632:
441:
302:
267:
68:
60:
55:into a double-covered
44:
32:Torus (disambiguation)
30:. For other uses, see
6407:Real projective plane
6392:Pretzel (genus 3) ...
5937:mathworld.wolfram.com
5700:Geometries and Groups
5635:Toroidal and poloidal
5595:Real projective plane
5464:
5260:
5239:
5220:
5174:
5139:embedded on the torus
5117:
4993:
4943:
4779:
4750:
4721:
4570:
4561:Further information:
4336:
4299:
4270:
4268:{\displaystyle C^{1}}
4248:
4218:
4170:
3927:
3744:
3588:
3541:
3503:
3474:
3437:
3393:
3377:
3369:
3342:; equivalently, as a
3306:
3253:
3154:
3127:
3101:
3057:
2964:
2924:
2805:
2769:
2736:
2707:
2674:
2645:
2598:
2464:
2390:
2253:
2225:
2123:
2085:
1905:toroidal and poloidal
1862:
1485:
1275:
1065:
907:
799:
782:Cartesian coordinates
762:
731:
708:
685:
633:
439:
303:
301:{\displaystyle S^{1}}
268:
93:surface of revolution
66:
50:
42:
6562:Euler characteristic
5570:Joint European Torus
5327:
5183:
5152:
5005:
4973:
4967:short exact sequence
4814:
4759:
4730:
4690:
4591:Euler characteristic
4316:
4279:
4252:
4223:, or in other words
4198:
4020:
3802:
3643:
3551:
3521:
3483:
3454:
3417:
3336:equilateral triangle
3269:
3205:
3081:
3037:
3022:-torus is 0 for all
3016:Euler characteristic
2944:
2904:
2870:; that is, a closed
2785:
2749:
2716:
2687:
2654:
2610:
2523:
2450:of the four points.
2273:
2150:
2103:
2065:
1574:
1308:
1183:
926:
812:
788:
743:
720:
697:
644:
452:
285:
237:
6296:(27 January 2014).
6258:Creation of a torus
5980:2006Sci...313...72T
5931:Weisstein, Eric W.
4684:mapping class group
4676:homeomorphism group
4573:toroidal polyhedron
4563:Toroidal polyhedron
4304:, with corrugations
4236:Nash-Kuiper theorem
3510:Riemannian manifold
3195:configuration space
3120:Configuration space
3115:Quasitoric manifold
3110:nontrivial cycles.
2485:, often called the
2481:n-dimensional torus
2440:conformal structure
2436:ramification points
2239:fundamental polygon
1290:Euclidean open disk
760:{\displaystyle R/r}
146:self-crossing torus
124:torus of revolution
6389:Number 8 (genus 2)
6231:Weisstein, Eric W.
6046:on 5 October 2008.
5848:Weisstein, Eric W.
5702:. Springer, 1987.
5684:Algebraic Topology
5655:Villarceau circles
5610:Surface (topology)
5540:Annulus (geometry)
5516:Mathematics portal
5459:
5416:
5397:
5362:
5302:De Bruijn sequence
5275:
5242:
5227:four color theorem
5215:
5169:
5112:
4988:
4938:
4774:
4745:
4716:
4680:geometric topology
4649:. You can help by
4584:
4557:Toroidal polyhedra
4484:handles attached.
4455:surfaces. A genus
4402:geodesic triangles
4371:Gaussian curvature
4331:
4306:
4294:
4265:
4213:
4165:
3922:
3739:
3630:Gaussian curvature
3583:
3536:
3498:
3469:
3432:
3407:
3388:
3372:
3301:
3248:
3179:
3149:
3096:
3052:
2986:free abelian group
2971:toral automorphism
2959:
2919:
2860:compact Lie groups
2800:
2764:
2731:
2702:
2669:
2640:
2593:
2589:
2582:
2516:circles. That is:
2504:holes or of genus
2475:
2457:-dimensional torus
2444:Weierstrass points
2385:
2256:
2220:
2118:
2080:
1934:list of references
1857:
1855:
1801:
1480:
1478:
1292:and a circle. The
1270:
1242:
1060:
902:
871:
794:
757:
726:
703:
680:
628:
626:
442:
298:
263:
221:, a ring torus is
126:, also known as a
120:axis of revolution
69:
61:
45:
6610:
6609:
6606:
6605:
6440:
6439:
6069:(19): 7218–7223.
5772:978-3-642-34363-6
5716:978-3-540-15281-1
5676:978-970-10-6596-9
5415:
4797:fundamental group
4667:
4666:
4554:
4553:
4523:projective planes
4443:In the theory of
4155:
4120:
4113:
3177:
2978:fundamental group
2973:on the quotient.
2934:integral matrices
2543:
2541:
2430:Two-sheeted cover
2260:fundamental group
2058:relative topology
1987:
1986:
1979:
1800:
1776:
1749:
1650:
1624:
1280:of this torus is
1220:
849:
797:{\displaystyle z}
729:{\displaystyle r}
706:{\displaystyle R}
359:Bottom-halves and
227:Cartesian product
202:, non-inflatable
6630:
6525:Triangulatedness
6505:
6368:
6364:Without boundary
6352:
6345:
6338:
6329:
6324:
6322:
6320:
6308:
6302:
6245:
6244:
6243:
6226:
6220:
6219:
6217:
6215:
6200:
6194:
6193:
6191:
6189:
6174:
6168:
6167:
6165:
6163:
6154:. Archived from
6148:
6142:
6141:
6139:
6137:
6117:
6111:
6110:
6108:
6106:
6088:
6078:
6054:
6048:
6047:
6042:. Archived from
6031:
6025:
6024:
6022:
5991:
5963:
5954:
5948:
5947:
5945:
5943:
5928:
5922:
5916:
5910:
5909:
5903:
5894:
5888:
5887:
5885:
5883:
5868:
5862:
5861:
5860:
5843:
5837:
5836:
5834:
5832:
5823:. Spatial Corp.
5817:
5811:
5810:
5808:
5806:
5791:
5785:
5784:
5741:
5518:
5513:
5512:
5492:
5468:
5466:
5465:
5460:
5446:
5445:
5430:
5429:
5417:
5408:
5402:
5401:
5367:
5366:
5271:
5259:
5224:
5222:
5221:
5216:
5205:
5204:
5203:
5202:
5178:
5176:
5175:
5170:
5168:
5167:
5166:
5165:
5143:chromatic number
5129:Coloring a torus
5121:
5119:
5118:
5113:
5102:
5101:
5096:
5084:
5083:
5068:
5067:
5062:
5041:
5040:
5035:
5023:
5022:
4997:
4995:
4994:
4989:
4987:
4986:
4981:
4947:
4945:
4944:
4939:
4931:
4905:
4904:
4899:
4869:
4868:
4844:
4843:
4838:
4826:
4825:
4801:cohomology group
4787:At the level of
4783:
4781:
4780:
4775:
4773:
4772:
4767:
4754:
4752:
4751:
4746:
4744:
4743:
4738:
4725:
4723:
4722:
4717:
4712:
4662:
4659:
4641:
4634:
4578:
4546:
4535:
4528:
4406:hyperbolic plane
4359:Riemann surfaces
4357:In the study of
4340:
4338:
4337:
4332:
4330:
4329:
4324:
4303:
4301:
4300:
4295:
4293:
4292:
4287:
4274:
4272:
4271:
4266:
4264:
4263:
4222:
4220:
4219:
4214:
4212:
4211:
4206:
4174:
4172:
4171:
4166:
4161:
4157:
4156:
4148:
4143:
4142:
4130:
4129:
4118:
4114:
4106:
4101:
4100:
4088:
4087:
4075:
4074:
4069:
4000:
3998:
3981:Hopf coordinates
3978:
3962:
3931:
3929:
3928:
3923:
3786:
3768:. It can not be
3748:
3746:
3745:
3740:
3624:
3592:
3590:
3589:
3584:
3582:
3581:
3576:
3570:
3565:
3564:
3559:
3546:
3545:
3543:
3542:
3537:
3535:
3534:
3529:
3507:
3505:
3504:
3499:
3497:
3496:
3491:
3478:
3476:
3475:
3470:
3468:
3467:
3462:
3441:
3439:
3438:
3433:
3431:
3430:
3425:
3344:triangular prism
3310:
3308:
3307:
3302:
3300:
3299:
3294:
3288:
3283:
3282:
3277:
3257:
3255:
3254:
3249:
3247:
3246:
3237:
3236:
3231:
3219:
3218:
3213:
3175:
3171:
3163:
3105:
3103:
3102:
3097:
3095:
3094:
3089:
3068:exterior algebra
3061:
3059:
3058:
3053:
3051:
3050:
3045:
2968:
2966:
2965:
2960:
2958:
2957:
2952:
2928:
2926:
2925:
2920:
2918:
2917:
2912:
2809:
2807:
2806:
2801:
2799:
2798:
2793:
2773:
2771:
2770:
2765:
2763:
2762:
2757:
2740:
2738:
2737:
2732:
2730:
2729:
2724:
2711:
2709:
2708:
2703:
2701:
2700:
2695:
2678:
2676:
2675:
2670:
2668:
2667:
2662:
2649:
2647:
2646:
2641:
2639:
2638:
2633:
2624:
2623:
2618:
2602:
2600:
2599:
2594:
2588:
2583:
2578:
2577:
2576:
2571:
2556:
2555:
2550:
2537:
2536:
2531:
2483:
2482:
2420:Hurewicz theorem
2414:of the torus is
2394:
2392:
2391:
2386:
2381:
2373:
2362:
2361:
2356:
2347:
2346:
2331:
2330:
2325:
2316:
2315:
2300:
2299:
2294:
2285:
2284:
2229:
2227:
2226:
2221:
2127:
2125:
2124:
2119:
2117:
2116:
2111:
2089:
2087:
2086:
2081:
2079:
2078:
2073:
1982:
1975:
1971:
1968:
1962:
1957:this section by
1948:inline citations
1927:
1926:
1919:
1899:
1895:
1891:
1884:
1880:
1876:
1866:
1864:
1863:
1858:
1856:
1849:
1848:
1812:
1811:
1802:
1793:
1787:
1786:
1781:
1777:
1772:
1761:
1754:
1750:
1745:
1734:
1728:
1727:
1668:
1667:
1655:
1651:
1646:
1635:
1629:
1625:
1620:
1609:
1603:
1602:
1569:
1568:
1566:
1565:
1562:
1559:
1541:
1540:
1538:
1537:
1534:
1531:
1513:
1509:
1502:
1498:
1489:
1487:
1486:
1481:
1479:
1472:
1471:
1459:
1458:
1443:
1439:
1424:
1420:
1419:
1418:
1378:
1377:
1362:
1358:
1343:
1339:
1279:
1277:
1276:
1271:
1269:
1268:
1256:
1255:
1243:
1241:
1240:
1235:
1234:
1221:
1219:
1218:
1206:
1205:
1196:
1194:
1193:
1175:
1161:
1155:
1145:
1139:
1117:
1105:
1093:
1079:
1075:
1069:
1067:
1066:
1061:
1056:
1052:
1051:
1050:
1038:
1037:
1023:
1022:
1007:
1006:
1001:
997:
996:
995:
983:
982:
970:
969:
957:
956:
944:
943:
920:quartic equation
911:
909:
908:
903:
898:
897:
885:
884:
872:
870:
869:
864:
863:
850:
848:
847:
835:
834:
825:
823:
822:
803:
801:
800:
795:
766:
764:
763:
758:
753:
735:
733:
732:
727:
712:
710:
709:
704:
689:
687:
686:
681:
637:
635:
634:
629:
627:
582:
518:
428:
417:
405:
394:
382:
371:
319:In the field of
307:
305:
304:
299:
297:
296:
272:
270:
269:
264:
262:
261:
249:
248:
82:
6640:
6639:
6633:
6632:
6631:
6629:
6628:
6627:
6613:
6612:
6611:
6602:
6566:
6543:Characteristics
6538:
6500:
6494:
6436:
6395:
6359:
6356:
6318:
6316:
6311:
6300:
6294:Séquin, Carlo H
6292:
6289:Wayback Machine
6254:
6249:
6248:
6234:"Torus Cutting"
6229:
6228:
6227:
6223:
6213:
6211:
6202:
6201:
6197:
6187:
6185:
6184:on 18 June 2012
6176:
6175:
6171:
6161:
6159:
6150:
6149:
6145:
6135:
6133:
6119:
6118:
6114:
6104:
6102:
6056:
6055:
6051:
6033:
6032:
6028:
6020:
5989:10.1.1.215.7449
5974:(5783): 72–74.
5961:
5956:
5955:
5951:
5941:
5939:
5930:
5929:
5925:
5917:
5913:
5901:
5896:
5895:
5891:
5881:
5879:
5870:
5869:
5865:
5846:
5845:
5844:
5840:
5830:
5828:
5819:
5818:
5814:
5804:
5802:
5793:
5792:
5788:
5773:
5743:
5742:
5738:
5733:
5681:Allen Hatcher.
5664:
5659:
5530:Algebraic torus
5514:
5507:
5504:
5488:
5437:
5421:
5396:
5395:
5383:
5382:
5372:
5361:
5360:
5348:
5347:
5331:
5325:
5324:
5314:
5312:Cutting a torus
5283:de Bruijn torus
5281:mathematics, a
5270:
5266:
5255:
5253:
5251:de Bruijn torus
5247:
5245:de Bruijn torus
5194:
5181:
5180:
5157:
5150:
5149:
5131:
5091:
5075:
5057:
5030:
5014:
5003:
5002:
4976:
4971:
4970:
4894:
4860:
4833:
4817:
4812:
4811:
4762:
4757:
4756:
4733:
4728:
4727:
4688:
4687:
4672:
4663:
4657:
4654:
4647:needs expansion
4576:
4565:
4559:
4547:
4536:
4459:surface is the
4441:
4431:
4355:
4347:surface normals
4319:
4314:
4313:
4282:
4277:
4276:
4255:
4250:
4249:
4201:
4196:
4195:
4134:
4121:
4092:
4079:
4064:
4033:
4029:
4018:
4017:
3996:
3991:
3976:
3944:
3800:
3799:
3777:
3641:
3640:
3598:
3595:Cartesian plane
3571:
3554:
3549:
3548:
3524:
3519:
3518:
3513:
3486:
3481:
3480:
3457:
3452:
3451:
3420:
3415:
3414:
3399:
3364:
3313:symmetric group
3289:
3272:
3267:
3266:
3238:
3226:
3208:
3203:
3202:
3173:
3169:
3162:
3143:, which is the
3142:
3122:
3117:
3084:
3079:
3078:
3040:
3035:
3034:
3028:cohomology ring
2947:
2942:
2941:
2907:
2902:
2901:
2853:complex numbers
2788:
2783:
2782:
2778:of the integer
2752:
2747:
2746:
2719:
2714:
2713:
2690:
2685:
2684:
2657:
2652:
2651:
2628:
2613:
2608:
2607:
2566:
2545:
2544:
2526:
2521:
2520:
2480:
2479:
2459:
2432:
2351:
2338:
2320:
2307:
2289:
2276:
2271:
2270:
2148:
2147:
2141:Cartesian plane
2106:
2101:
2100:
2068:
2063:
2062:
1996:defined as the
1992:, a torus is a
1983:
1972:
1966:
1963:
1952:
1938:related reading
1928:
1924:
1917:
1903:In modern use,
1897:
1893:
1889:
1882:
1878:
1874:
1854:
1853:
1840:
1803:
1762:
1756:
1755:
1735:
1729:
1719:
1709:
1703:
1702:
1659:
1636:
1630:
1610:
1604:
1594:
1584:
1572:
1571:
1563:
1560:
1551:
1550:
1548:
1543:
1535:
1532:
1523:
1522:
1520:
1515:
1511:
1507:
1500:
1493:
1477:
1476:
1463:
1450:
1429:
1425:
1410:
1406:
1402:
1395:
1389:
1388:
1369:
1348:
1344:
1329:
1325:
1318:
1306:
1305:
1260:
1247:
1228:
1210:
1197:
1181:
1180:
1167:
1157:
1150:
1141:
1134:
1109:
1097:
1085:
1077:
1073:
1042:
1029:
1028:
1024:
1014:
987:
974:
961:
948:
935:
934:
930:
929:
924:
923:
889:
876:
857:
839:
826:
810:
809:
786:
785:
741:
740:
718:
717:
695:
694:
642:
641:
625:
624:
605:
584:
583:
541:
520:
519:
477:
450:
449:
444:A torus can be
434:
433:
432:
431:
430:
420:
418:
409:
408:
407:
397:
395:
386:
385:
384:
374:
372:
363:
362:
360:
354:
341:
312:, a surface in
288:
283:
282:
275:Euclidean space
253:
240:
235:
234:
35:
24:
17:
12:
11:
5:
6638:
6637:
6634:
6626:
6625:
6615:
6614:
6608:
6607:
6604:
6603:
6601:
6600:
6595:
6589:
6583:
6580:
6574:
6572:
6568:
6567:
6565:
6564:
6559:
6554:
6546:
6544:
6540:
6539:
6537:
6536:
6531:
6522:
6517:
6511:
6509:
6502:
6496:
6495:
6493:
6492:
6486:
6485:
6484:
6474:
6473:
6472:
6467:
6459:
6458:
6457:
6448:
6446:
6442:
6441:
6438:
6437:
6435:
6434:
6431:Dyck's surface
6428:
6422:
6421:
6420:
6415:
6403:
6401:
6400:Non-orientable
6397:
6396:
6394:
6393:
6390:
6387:
6381:
6374:
6372:
6365:
6361:
6360:
6357:
6355:
6354:
6347:
6340:
6332:
6326:
6325:
6309:
6281:
6276:
6270:
6264:
6253:
6252:External links
6250:
6247:
6246:
6221:
6195:
6169:
6158:on 5 July 2012
6143:
6112:
6049:
6026:
5949:
5923:
5911:
5889:
5863:
5838:
5812:
5786:
5771:
5735:
5734:
5732:
5729:
5728:
5727:
5719:
5696:
5679:
5663:
5660:
5658:
5657:
5652:
5647:
5642:
5637:
5632:
5627:
5622:
5617:
5612:
5607:
5605:Spiric section
5602:
5597:
5592:
5590:Period lattice
5587:
5582:
5577:
5572:
5567:
5562:
5560:Elliptic curve
5557:
5552:
5547:
5545:Clifford torus
5542:
5537:
5535:Angenent torus
5532:
5527:
5521:
5520:
5519:
5503:
5500:
5499:
5498:
5470:
5469:
5458:
5455:
5452:
5449:
5444:
5440:
5436:
5433:
5428:
5424:
5420:
5414:
5411:
5405:
5400:
5394:
5391:
5388:
5385:
5384:
5381:
5378:
5377:
5375:
5370:
5365:
5359:
5356:
5353:
5350:
5349:
5346:
5343:
5340:
5337:
5336:
5334:
5313:
5310:
5268:
5249:Main article:
5246:
5243:
5214:
5211:
5208:
5201:
5197:
5191:
5188:
5164:
5160:
5147:complete graph
5135:Heawood number
5130:
5127:
5123:
5122:
5111:
5108:
5105:
5100:
5095:
5090:
5087:
5082:
5078:
5074:
5071:
5066:
5061:
5056:
5053:
5050:
5047:
5044:
5039:
5034:
5029:
5026:
5021:
5017:
5013:
5010:
4985:
4980:
4949:
4948:
4937:
4934:
4930:
4926:
4923:
4920:
4917:
4914:
4911:
4908:
4903:
4898:
4893:
4890:
4887:
4884:
4881:
4878:
4875:
4872:
4867:
4863:
4859:
4856:
4853:
4850:
4847:
4842:
4837:
4832:
4829:
4824:
4820:
4803:generates the
4771:
4766:
4742:
4737:
4715:
4711:
4707:
4704:
4701:
4698:
4695:
4671:
4668:
4665:
4664:
4644:
4642:
4558:
4555:
4552:
4551:
4540:
4433:Main article:
4430:
4423:
4354:
4351:
4328:
4323:
4291:
4286:
4262:
4258:
4210:
4205:
4178:Other tori in
4176:
4175:
4164:
4160:
4154:
4151:
4146:
4141:
4137:
4133:
4128:
4124:
4117:
4112:
4109:
4104:
4099:
4095:
4091:
4086:
4082:
4078:
4073:
4068:
4063:
4060:
4057:
4054:
4051:
4048:
4045:
4042:
4039:
4036:
4032:
4028:
4025:
3933:
3932:
3921:
3918:
3915:
3912:
3909:
3906:
3903:
3900:
3897:
3894:
3891:
3888:
3885:
3882:
3879:
3876:
3873:
3870:
3867:
3864:
3861:
3858:
3855:
3852:
3849:
3846:
3843:
3840:
3837:
3834:
3831:
3828:
3825:
3822:
3819:
3816:
3813:
3810:
3807:
3750:
3749:
3738:
3735:
3732:
3729:
3726:
3723:
3720:
3717:
3714:
3711:
3708:
3705:
3702:
3699:
3696:
3693:
3690:
3687:
3684:
3681:
3678:
3675:
3672:
3669:
3666:
3663:
3660:
3657:
3654:
3651:
3648:
3580:
3575:
3569:
3563:
3558:
3533:
3528:
3495:
3490:
3479:isomorphic to
3466:
3461:
3429:
3424:
3397:
3363:
3360:
3356:musical triads
3298:
3293:
3287:
3281:
3276:
3245:
3241:
3235:
3230:
3225:
3222:
3217:
3212:
3193:-torus is the
3185:-torus is the
3140:
3121:
3118:
3093:
3088:
3049:
3044:
2998:homology group
2956:
2951:
2916:
2911:
2797:
2792:
2761:
2756:
2728:
2723:
2699:
2694:
2666:
2661:
2637:
2632:
2627:
2622:
2617:
2604:
2603:
2592:
2587:
2581:
2575:
2570:
2565:
2562:
2559:
2554:
2549:
2540:
2535:
2530:
2495:
2491:
2484:
2467:Clifford torus
2458:
2452:
2431:
2428:
2412:homology group
2396:
2395:
2384:
2380:
2376:
2372:
2368:
2365:
2360:
2355:
2350:
2345:
2341:
2337:
2334:
2329:
2324:
2319:
2314:
2310:
2306:
2303:
2298:
2293:
2288:
2283:
2279:
2264:direct product
2231:
2230:
2218:
2215:
2212:
2209:
2206:
2203:
2200:
2197:
2194:
2191:
2188:
2185:
2182:
2179:
2176:
2173:
2170:
2167:
2164:
2161:
2158:
2155:
2115:
2110:
2077:
2072:
2027:Clifford torus
1994:closed surface
1985:
1984:
1942:external links
1931:
1929:
1922:
1916:
1913:
1852:
1847:
1843:
1839:
1836:
1833:
1830:
1827:
1824:
1821:
1818:
1815:
1810:
1806:
1799:
1796:
1790:
1785:
1780:
1775:
1771:
1768:
1765:
1759:
1753:
1748:
1744:
1741:
1738:
1732:
1726:
1722:
1718:
1715:
1712:
1710:
1708:
1705:
1704:
1701:
1698:
1695:
1692:
1689:
1686:
1683:
1680:
1677:
1674:
1671:
1666:
1662:
1658:
1654:
1649:
1645:
1642:
1639:
1633:
1628:
1623:
1619:
1616:
1613:
1607:
1601:
1597:
1593:
1590:
1587:
1585:
1583:
1580:
1579:
1475:
1470:
1466:
1462:
1457:
1453:
1449:
1446:
1442:
1438:
1435:
1432:
1428:
1423:
1417:
1413:
1409:
1405:
1401:
1398:
1396:
1394:
1391:
1390:
1387:
1384:
1381:
1376:
1372:
1368:
1365:
1361:
1357:
1354:
1351:
1347:
1342:
1338:
1335:
1332:
1328:
1324:
1321:
1319:
1317:
1314:
1313:
1267:
1263:
1259:
1254:
1250:
1246:
1239:
1233:
1227:
1224:
1217:
1213:
1209:
1204:
1200:
1192:
1164:
1163:
1147:
1131:
1107:
1095:
1059:
1055:
1049:
1045:
1041:
1036:
1032:
1027:
1021:
1017:
1013:
1010:
1005:
1000:
994:
990:
986:
981:
977:
973:
968:
964:
960:
955:
951:
947:
942:
938:
933:
901:
896:
892:
888:
883:
879:
875:
868:
862:
856:
853:
846:
842:
838:
833:
829:
821:
793:
767:is called the
756:
752:
748:
725:
702:
679:
676:
673:
670:
667:
664:
661:
658:
655:
652:
649:
623:
620:
617:
614:
611:
608:
606:
604:
601:
598:
595:
592:
589:
586:
585:
581:
577:
574:
571:
568:
565:
562:
559:
556:
553:
550:
547:
544:
542:
540:
537:
534:
531:
528:
525:
522:
521:
517:
513:
510:
507:
504:
501:
498:
495:
492:
489:
486:
483:
480:
478:
476:
473:
470:
467:
464:
461:
458:
457:
419:
412:
411:
410:
396:
389:
388:
387:
373:
366:
365:
364:
358:
357:
356:
355:
353:
350:
340:
337:
310:Clifford torus
295:
291:
260:
256:
252:
247:
243:
175:ringette rings
15:
13:
10:
9:
6:
4:
3:
2:
6636:
6635:
6624:
6621:
6620:
6618:
6599:
6596:
6594:
6590:
6588:
6584:
6582:Making a hole
6581:
6579:
6578:Connected sum
6576:
6575:
6573:
6569:
6563:
6560:
6558:
6555:
6552:
6548:
6547:
6545:
6541:
6535:
6534:Orientability
6532:
6530:
6526:
6523:
6521:
6518:
6516:
6515:Connectedness
6513:
6512:
6510:
6506:
6503:
6497:
6490:
6487:
6483:
6480:
6479:
6478:
6475:
6471:
6468:
6466:
6463:
6462:
6460:
6455:
6454:
6453:
6450:
6449:
6447:
6445:With boundary
6443:
6433:(genus 3) ...
6432:
6429:
6426:
6423:
6419:
6418:Roman surface
6416:
6414:
6413:Boy's surface
6410:
6409:
6408:
6405:
6404:
6402:
6398:
6391:
6388:
6385:
6382:
6379:
6376:
6375:
6373:
6369:
6366:
6362:
6353:
6348:
6346:
6341:
6339:
6334:
6333:
6330:
6315:
6314:"Torus Earth"
6310:
6306:
6299:
6295:
6290:
6286:
6282:
6280:
6277:
6274:
6271:
6268:
6265:
6263:
6259:
6256:
6255:
6251:
6241:
6240:
6235:
6232:
6225:
6222:
6210:
6206:
6199:
6196:
6183:
6179:
6173:
6170:
6157:
6153:
6147:
6144:
6131:
6127:
6123:
6116:
6113:
6100:
6096:
6092:
6087:
6082:
6077:
6072:
6068:
6064:
6060:
6053:
6050:
6045:
6041:
6037:
6030:
6027:
6019:
6015:
6011:
6007:
6003:
5999:
5995:
5990:
5985:
5981:
5977:
5973:
5969:
5968:
5960:
5953:
5950:
5938:
5934:
5927:
5924:
5921:
5915:
5912:
5907:
5900:
5893:
5890:
5877:
5873:
5867:
5864:
5858:
5857:
5852:
5849:
5842:
5839:
5826:
5822:
5816:
5813:
5800:
5796:
5790:
5787:
5782:
5778:
5774:
5768:
5764:
5760:
5756:
5755:
5750:
5746:
5745:Gallier, Jean
5740:
5737:
5730:
5726:
5725:
5720:
5717:
5713:
5709:
5708:3-540-15281-4
5705:
5701:
5697:
5694:
5693:0-521-79540-0
5690:
5686:
5685:
5680:
5677:
5673:
5669:
5666:
5665:
5661:
5656:
5653:
5651:
5650:Umbilic torus
5648:
5646:
5643:
5641:
5638:
5636:
5633:
5631:
5628:
5626:
5625:Toric variety
5623:
5621:
5620:Toric section
5618:
5616:
5613:
5611:
5608:
5606:
5603:
5601:
5598:
5596:
5593:
5591:
5588:
5586:
5585:Maximal torus
5583:
5581:
5578:
5576:
5573:
5571:
5568:
5566:
5563:
5561:
5558:
5556:
5555:Dupin cyclide
5553:
5551:
5550:Complex torus
5548:
5546:
5543:
5541:
5538:
5536:
5533:
5531:
5528:
5526:
5523:
5522:
5517:
5511:
5506:
5501:
5496:
5491:
5486:
5485:
5484:
5482:
5478:
5473:
5453:
5450:
5447:
5442:
5438:
5434:
5431:
5426:
5422:
5412:
5409:
5403:
5398:
5392:
5389:
5386:
5379:
5373:
5368:
5363:
5357:
5354:
5351:
5344:
5341:
5338:
5332:
5323:
5322:
5321:
5319:
5311:
5309:
5307:
5303:
5299:
5296:
5292:
5288:
5284:
5280:
5279:combinatorial
5272:
5263:
5258:
5252:
5244:
5238:
5234:
5232:
5228:
5212:
5209:
5186:
5148:
5144:
5140:
5136:
5128:
5126:
5109:
5098:
5085:
5080:
5076:
5064:
5051:
5048:
5037:
5024:
5019:
5015:
5008:
5001:
5000:
4999:
4983:
4968:
4963:
4961:
4957:
4954:
4935:
4924:
4921:
4915:
4912:
4909:
4901:
4888:
4885:
4882:
4873:
4865:
4861:
4854:
4851:
4848:
4840:
4827:
4822:
4818:
4810:
4809:
4808:
4806:
4802:
4798:
4794:
4790:
4785:
4769:
4740:
4705:
4702:
4696:
4693:
4685:
4681:
4677:
4670:Automorphisms
4669:
4661:
4652:
4648:
4645:This section
4643:
4640:
4636:
4635:
4632:
4630:
4625:
4623:
4619:
4615:
4611:
4607:
4603:
4599:
4595:
4592:
4588:
4581:
4580:quadrilateral
4574:
4569:
4564:
4556:
4550:
4545:
4541:
4539:
4534:
4530:
4526:
4524:
4520:
4517:
4513:
4508:
4506:
4502:
4498:
4494:
4490:
4485:
4483:
4479:
4475:
4471:
4466:
4462:
4461:connected sum
4458:
4454:
4450:
4446:
4440:
4438:
4428:
4424:
4422:
4419:
4414:
4412:
4407:
4403:
4399:
4395:
4390:
4386:
4382:
4380:
4376:
4372:
4368:
4364:
4360:
4352:
4350:
4348:
4344:
4326:
4311:
4289:
4260:
4256:
4247:
4243:
4241:
4237:
4233:
4228:
4226:
4208:
4193:
4189:
4185:
4181:
4162:
4158:
4152:
4149:
4144:
4139:
4135:
4131:
4126:
4122:
4115:
4110:
4107:
4102:
4097:
4093:
4089:
4084:
4080:
4076:
4071:
4061:
4055:
4052:
4049:
4046:
4043:
4040:
4037:
4030:
4026:
4023:
4016:
4015:
4014:
4012:
4008:
4004:
3994:
3989:
3986:
3982:
3974:
3971:, and 0 <
3970:
3966:
3960:
3956:
3952:
3948:
3942:
3938:
3919:
3913:
3910:
3907:
3904:
3901:
3898:
3895:
3892:
3886:
3883:
3880:
3877:
3874:
3871:
3865:
3862:
3859:
3856:
3850:
3847:
3844:
3841:
3838:
3835:
3826:
3820:
3817:
3814:
3811:
3808:
3798:
3797:
3796:
3794:
3790:
3784:
3780:
3775:
3771:
3767:
3763:
3762:diffeomorphic
3759:
3755:
3733:
3730:
3727:
3724:
3721:
3718:
3715:
3712:
3709:
3706:
3703:
3700:
3697:
3694:
3691:
3688:
3685:
3682:
3679:
3673:
3667:
3664:
3661:
3658:
3655:
3652:
3649:
3639:
3638:
3637:
3634:
3631:
3626:
3622:
3618:
3614:
3610:
3606:
3602:
3596:
3578:
3567:
3561:
3531:
3516:
3511:
3493:
3464:
3449:
3445:
3427:
3412:
3404:
3400:
3392:
3385:
3381:
3376:
3368:
3361:
3359:
3357:
3353:
3348:
3345:
3341:
3337:
3333:
3329:
3325:
3320:
3318:
3314:
3296:
3285:
3279:
3265:
3261:
3243:
3233:
3220:
3215:
3200:
3196:
3192:
3188:
3184:
3167:
3160:
3159:
3153:
3146:
3139:
3135:
3131:
3126:
3119:
3116:
3111:
3109:
3091:
3077:
3073:
3069:
3065:
3047:
3032:
3029:
3025:
3021:
3017:
3013:
3010:
3007:
3003:
2999:
2995:
2991:
2987:
2983:
2979:
2974:
2972:
2954:
2939:
2935:
2932:
2914:
2899:
2895:
2894:Automorphisms
2891:
2889:
2885:
2881:
2877:
2873:
2869:
2868:maximal torus
2865:
2861:
2856:
2854:
2850:
2846:
2843:
2839:
2836:
2832:
2828:
2823:
2821:
2818:-dimensional
2817:
2813:
2795:
2781:
2777:
2759:
2744:
2726:
2697:
2682:
2664:
2635:
2625:
2620:
2590:
2585:
2579:
2573:
2563:
2560:
2557:
2552:
2538:
2533:
2519:
2518:
2517:
2515:
2511:
2507:
2503:
2499:
2493:
2489:
2486:
2478:
2472:
2468:
2463:
2456:
2453:
2451:
2449:
2445:
2441:
2437:
2429:
2427:
2425:
2421:
2417:
2413:
2408:
2404:
2401:
2382:
2374:
2366:
2358:
2343:
2339:
2335:
2327:
2312:
2308:
2304:
2296:
2281:
2277:
2269:
2268:
2267:
2265:
2261:
2252:
2248:
2246:
2243:
2240:
2236:
2216:
2210:
2207:
2204:
2201:
2198:
2192:
2186:
2183:
2180:
2177:
2174:
2168:
2162:
2159:
2156:
2146:
2145:
2144:
2142:
2138:
2133:
2131:
2113:
2098:
2094:
2090:
2075:
2059:
2054:
2052:
2048:
2044:
2040:
2036:
2032:
2028:
2024:
2021:
2017:
2016:
2011:
2008: ×
2007:
2003:
1999:
1995:
1991:
1990:Topologically
1981:
1978:
1970:
1967:November 2015
1960:
1956:
1950:
1949:
1943:
1939:
1935:
1930:
1921:
1920:
1914:
1912:
1910:
1906:
1901:
1886:
1872:
1867:
1850:
1845:
1837:
1834:
1831:
1822:
1819:
1816:
1808:
1804:
1797:
1794:
1788:
1783:
1778:
1773:
1769:
1766:
1763:
1757:
1751:
1746:
1742:
1739:
1736:
1730:
1724:
1720:
1716:
1713:
1711:
1706:
1699:
1693:
1690:
1687:
1678:
1675:
1672:
1664:
1660:
1656:
1652:
1647:
1643:
1640:
1637:
1631:
1626:
1621:
1617:
1614:
1611:
1605:
1599:
1595:
1591:
1588:
1586:
1581:
1558:
1554:
1546:
1530:
1526:
1518:
1504:
1497:
1490:
1473:
1468:
1464:
1460:
1455:
1451:
1447:
1444:
1440:
1436:
1433:
1430:
1426:
1421:
1415:
1411:
1407:
1403:
1399:
1397:
1392:
1385:
1382:
1379:
1374:
1370:
1366:
1363:
1359:
1355:
1352:
1349:
1345:
1340:
1336:
1333:
1330:
1326:
1322:
1320:
1315:
1303:
1299:
1295:
1291:
1287:
1283:
1282:diffeomorphic
1265:
1261:
1257:
1252:
1248:
1244:
1237:
1225:
1222:
1215:
1211:
1207:
1202:
1198:
1179:
1174:
1170:
1160:
1153:
1148:
1144:
1137:
1132:
1129:
1128:
1123:
1122:
1116:
1112:
1108:
1104:
1100:
1096:
1092:
1088:
1083:
1082:
1081:
1070:
1057:
1053:
1047:
1043:
1039:
1034:
1030:
1025:
1019:
1015:
1011:
1008:
1003:
998:
992:
988:
984:
979:
975:
971:
966:
962:
958:
953:
949:
945:
940:
936:
931:
921:
917:
912:
899:
894:
890:
886:
881:
877:
873:
866:
854:
851:
844:
840:
836:
831:
827:
807:
791:
783:
779:
774:
772:
771:
754:
750:
746:
737:
723:
716:
700:
693:
677:
671:
668:
665:
662:
656:
653:
650:
647:
638:
621:
618:
615:
612:
609:
607:
599:
596:
593:
587:
579:
575:
572:
566:
563:
560:
557:
554:
551:
545:
543:
535:
532:
529:
523:
515:
511:
508:
502:
499:
496:
493:
490:
487:
481:
479:
471:
468:
465:
459:
447:
438:
427:
423:
416:
404:
400:
393:
381:
377:
370:
351:
349:
347:
346:
338:
336:
334:
328:
326:
322:
317:
315:
311:
293:
289:
280:
276:
258:
254:
250:
245:
241:
232:
228:
224:
220:
215:
213:
209:
205:
201:
197:
193:
189:
185:
184:
178:
176:
172:
168:
163:
161:
160:
155:
151:
147:
143:
142:
141:spindle torus
137:
133:
129:
125:
121:
116:
114:
110:
106:
102:
98:
94:
90:
86:
78:
74:
65:
58:
54:
49:
41:
37:
33:
29:
22:
6477:Möbius strip
6425:Klein bottle
6383:
6317:. Retrieved
6285:Ghostarchive
6283:Archived at
6262:cut-the-knot
6237:
6224:
6212:. Retrieved
6208:
6198:
6186:. Retrieved
6182:the original
6172:
6160:. Retrieved
6156:the original
6146:
6134:. Retrieved
6126:Sci-News.com
6125:
6115:
6103:. Retrieved
6066:
6062:
6052:
6044:the original
6029:
5971:
5965:
5952:
5940:. Retrieved
5936:
5926:
5914:
5905:
5892:
5880:. Retrieved
5875:
5866:
5854:
5841:
5829:. Retrieved
5815:
5803:. Retrieved
5789:
5753:
5739:
5723:
5699:
5683:
5667:
5575:Klein bottle
5480:
5476:
5474:
5471:
5317:
5315:
5305:
5294:
5290:
5282:
5276:
5265:
5133:The torus's
5132:
5124:
4964:
4959:
4955:
4950:
4786:
4673:
4655:
4651:adding to it
4646:
4626:
4621:
4617:
4613:
4609:
4605:
4601:
4597:
4593:
4585:
4509:
4505:triple torus
4501:double torus
4496:
4492:
4486:
4481:
4473:
4469:
4464:
4456:
4452:
4442:
4436:
4426:
4417:
4415:
4410:
4397:
4393:
4388:
4384:
4383:
4378:
4375:moduli space
4356:
4309:
4307:
4239:
4231:
4229:
4224:
4191:
4187:
4183:
4179:
4177:
4010:
3992:
3987:
3972:
3968:
3964:
3958:
3954:
3950:
3946:
3940:
3936:
3934:
3792:
3782:
3778:
3770:analytically
3757:
3753:
3751:
3635:
3627:
3620:
3616:
3612:
3608:
3604:
3600:
3514:
3447:
3443:
3408:
3383:
3349:
3331:
3328:Möbius strip
3323:
3321:
3316:
3259:
3198:
3190:
3186:
3182:
3180:
3156:
3145:Möbius strip
3137:
3133:
3107:
3071:
3063:
3030:
3023:
3019:
3011:
3005:
3001:
2993:
2989:
2984:-torus is a
2981:
2975:
2970:
2937:
2897:
2892:
2879:
2875:
2863:
2857:
2833:dimensional
2830:
2826:
2824:
2815:
2811:
2742:
2680:
2605:
2513:
2509:
2505:
2501:
2497:
2487:
2476:
2470:
2454:
2433:
2409:
2405:
2397:
2257:
2244:
2241:
2232:
2134:
2129:
2093:homeomorphic
2055:
2046:
2043:fiber bundle
2038:
2030:
2022:
2014:
2009:
2005:
1988:
1973:
1964:
1953:Please help
1945:
1902:
1887:
1868:
1556:
1552:
1544:
1528:
1524:
1516:
1505:
1495:
1491:
1298:surface area
1172:
1168:
1165:
1158:
1151:
1142:
1135:
1125:
1119:
1114:
1110:
1102:
1098:
1090:
1086:
1071:
913:
780:equation in
775:
770:aspect ratio
768:
738:
715:minor radius
714:
692:major radius
691:
639:
446:parametrized
443:
425:
421:
406:: horn torus
402:
398:
379:
375:
343:
342:
333:Klein bottle
329:
318:
223:homeomorphic
216:
195:
181:
179:
164:
157:
149:
145:
139:
135:
127:
123:
117:
112:
108:
88:
84:
76:
70:
36:
6520:Compactness
6305:Brady Haran
6209:Science4All
5831:16 November
5267:(16,32;3,3)
4549:genus three
4013:defined by
3403:duocylinder
2849:unit circle
2774:modulo the
2448:cross-ratio
2400:closed path
2235:unit square
2051:Hopf bundle
2029:. In fact,
1959:introducing
1499:and radius
916:square root
196:solid torus
183:solid torus
171:inner tubes
53:degenerates
28:Solid torus
6571:Operations
6553:components
6549:Number of
6529:smoothness
6508:Properties
6456:Semisphere
6371:Orientable
6267:"4D torus"
6214:1 November
5908:: 638–648.
5872:"poloidal"
5749:Xu, Dianna
5731:References
5645:Torus knot
5615:Toric lens
4805:cohomology
4658:April 2010
4629:immersions
4577:6 × 4 = 24
4489:two-sphere
3772:embedded (
3384:flat torus
3362:Flat torus
3113:See also:
2931:invertible
2745:-torus is
2494:hypertorus
2416:isomorphic
2410:The first
2035:filled out
1570:), yields
1304:, giving:
739:The ratio
167:swim rings
136:horn torus
128:ring torus
6598:Immersion
6593:cross-cap
6591:Gluing a
6585:Gluing a
6482:Cross-cap
6427:(genus 2)
6411:genus 1;
6386:(genus 1)
6380:(genus 0)
6239:MathWorld
5984:CiteSeerX
5882:10 August
5856:MathWorld
5390:−
5355:−
5187:χ
5107:→
5086:
5073:→
5052:
5046:→
5025:
5012:→
4965:Thus the
4916:
4889:
4862:π
4855:
4828:
4807:algebra:
4697:
4587:Polyhedra
4538:genus two
4519:connected
4077:∣
4062:∈
4003:congruent
3953:) = (cos(
3911:
3896:
3884:
3860:
3848:
3776:of class
3766:isometric
3731:
3716:
3701:
3686:
3338:, with a
3260:unordered
3070:over the
2888:manifolds
2845:Lie group
2820:hypercube
2580:⏟
2564:×
2561:⋯
2558:×
2375:×
2367:≅
2340:π
2336:×
2309:π
2278:π
2193:∼
2169:∼
1911:devices.
1835:−
1805:π
1767:−
1721:π
1691:−
1661:π
1641:−
1596:π
1452:π
1434:π
1408:π
1371:π
1353:π
1334:π
1223:−
985:−
852:−
672:π
657:∈
654:φ
648:θ
622:θ
619:
600:φ
594:θ
580:φ
576:
567:θ
564:
536:φ
530:θ
516:φ
512:
503:θ
500:
472:φ
466:θ
339:Etymology
279:embedding
251:×
208:doughnuts
204:lifebuoys
6623:Surfaces
6617:Category
6551:boundary
6470:Cylinder
6287:and the
6130:Archived
6099:Archived
6095:22523238
6018:Archived
6006:16825563
5825:Archived
5799:Archived
5751:(2013).
5502:See also
5229:for the
4793:homology
4789:homotopy
4620:, where
4478:2-sphere
4445:surfaces
4190:, where
4007:boundary
3990:, where
3985:3-sphere
3791:it into
3446:, where
3411:quotient
3378:Seen in
3264:orbifold
3130:orbifold
2988:of rank
2936:of size
2872:subgroup
2838:manifold
2683:-torus,
2438:. Every
2137:quotient
2020:3-sphere
1915:Topology
1178:interior
918:gives a
778:implicit
352:Geometry
321:topology
219:topology
198:include
113:doughnut
105:coplanar
73:geometry
6501:notions
6499:Related
6465:Annulus
6461:Ribbon
6319:24 July
6301:(video)
6188:21 July
6162:21 July
6136:21 July
6105:21 July
6086:3358891
6014:2877171
5976:Bibcode
5967:Science
5942:27 July
5933:"Torus"
5851:"Torus"
5821:"Torus"
5805:21 July
5781:3026641
5525:3-torus
5493:in the
5490:A003600
4616:= 2 − 2
4516:compact
4439:surface
4429:surface
4404:in the
4343:fractal
3957:), sin(
3789:Mapping
3382:, a 4D
3181:As the
3174:(G♭-B♭)
3170:(F♯-A♯)
3158:Tonnetz
3062:,
3018:of the
2884:protori
2842:abelian
2835:compact
2780:lattice
2424:abelian
2139:of the
2002:circles
2000:of two
1998:product
1955:improve
1567:
1549:
1539:
1521:
1286:product
314:4-space
231:circles
229:of two
225:to the
206:, ring
200:O-rings
132:tangent
118:If the
91:) is a
89:toruses
6587:handle
6378:Sphere
6093:
6083:
6012:
6004:
5986:
5779:
5769:
5714:
5706:
5691:
5674:
5630:Toroid
5600:Sphere
5298:matrix
5285:is an
5141:has a
4682:. Its
4435:Genus
4425:Genus
4119:
3781:, 2 ≤
3774:smooth
3752:where
3076:module
3026:. The
3009:choose
3000:of an
2992:. The
2980:of an
2776:action
2490:-torus
2473:-plane
1294:volume
1176:, the
212:bagels
210:, and
192:volume
159:toroid
154:sphere
97:circle
57:sphere
21:Taurus
6557:Genus
6384:Torus
6021:(PDF)
6010:S2CID
5962:(PDF)
5902:(PDF)
5662:Notes
5287:array
5231:plane
5049:Homeo
5016:Homeo
4582:faces
4575:with
4480:with
4449:genus
4394:three
3975:<
3963:then
3615:) ~ (
3611:+ 1,
3607:) ~ (
3396:{4,4}
3340:twist
2091:, is
2060:from
2049:(the
2045:over
2041:as a
1940:, or
1288:of a
1166:When
1149:When
1133:When
1127:apple
1121:lemon
1113:<
1089:>
1084:When
424:<
378:>
345:Torus
327:one.
325:genus
109:donut
77:torus
6452:Disk
6321:2019
6216:2022
6190:2012
6164:2012
6138:2012
6107:2012
6091:PMID
6002:PMID
5944:2021
5884:2007
5833:2014
5807:2012
5767:ISBN
5712:ISBN
5704:ISBN
5689:ISBN
5672:ISBN
5495:OEIS
5293:-by-
4791:and
4674:The
4510:The
4503:and
3939:and
3756:and
3623:+ 1)
3322:For
3155:The
2996:-th
2976:The
2258:The
1881:and
1542:and
1258:<
1076:and
806:axis
448:as:
188:disk
173:and
144:(or
85:tori
75:, a
6527:or
6491:...
6260:at
6081:PMC
6071:doi
6067:109
5994:doi
5972:313
5759:doi
5277:In
5262:STL
5233:.)
5081:TOP
5077:MCG
4886:Aut
4852:Aut
4819:MCG
4653:.
4463:of
3935:If
3908:cos
3893:sin
3881:sin
3857:cos
3845:sin
3785:≤ ∞
3728:sin
3713:cos
3698:sin
3683:cos
3517:=
3413:,
3398:1,0
3315:on
3197:of
2896:of
2825:An
2492:or
2426:).
2242:ABA
2053:).
2033:is
1154:= 0
1138:= 0
808:is
776:An
616:sin
573:sin
561:cos
509:cos
497:cos
335:).
281:of
233::
217:In
177:.
148:or
111:or
99:in
87:or
81:pl.
71:In
6619::
6303:.
6291::
6236:.
6207:.
6128:.
6124:.
6097:.
6089:.
6079:.
6065:.
6061:.
6038:.
6016:.
6008:.
6000:.
5992:.
5982:.
5970:.
5964:.
5935:.
5904:.
5874:.
5853:.
5777:MR
5775:.
5765:.
5747:;
5710:,
5670:,
5497:).
5110:1.
4913:GL
4823:Ho
4694:GL
4612:+
4608:−
4600:+
4596:−
4571:A
4525:.
4451:"
4418:M*
4411:M*
4398:M*
4389:M*
3999:/4
3995:=
3967:,
3961:))
3949:,
3619:,
3603:,
3547::
3358:.
2890:.
2831:n-
2471:xz
2247:.
2132:.
2004::
1944:,
1936:,
1555:−
1547:=
1527:+
1519:=
1494:2π
1171:≥
1101:=
1080::
922:,
316:.
214:.
169:,
115:.
83::
6351:e
6344:t
6337:v
6323:.
6307:.
6242:.
6218:.
6192:.
6166:.
6140:.
6109:.
6073::
5996::
5978::
5946:.
5886:.
5859:.
5835:.
5809:.
5783:.
5761::
5718:.
5695:.
5481:n
5477:n
5457:)
5454:n
5451:8
5448:+
5443:2
5439:n
5435:3
5432:+
5427:3
5423:n
5419:(
5413:6
5410:1
5404:=
5399:)
5393:1
5387:n
5380:n
5374:(
5369:+
5364:)
5358:1
5352:n
5345:2
5342:+
5339:n
5333:(
5318:n
5306:n
5295:n
5291:m
5269:2
5213:7
5210:=
5207:)
5200:7
5196:K
5190:(
5163:7
5159:K
5104:)
5099:n
5094:T
5089:(
5070:)
5065:n
5060:T
5055:(
5043:)
5038:n
5033:T
5028:(
5020:0
5009:1
4984:n
4979:R
4960:G
4958:(
4956:K
4936:.
4933:)
4929:Z
4925:,
4922:n
4919:(
4910:=
4907:)
4902:n
4897:Z
4892:(
4883:=
4880:)
4877:)
4874:X
4871:(
4866:1
4858:(
4849:=
4846:)
4841:n
4836:T
4831:(
4770:n
4765:Z
4741:n
4736:R
4714:)
4710:Z
4706:,
4703:n
4700:(
4660:)
4656:(
4622:N
4618:N
4614:F
4610:E
4606:V
4602:F
4598:E
4594:V
4497:n
4493:n
4482:g
4474:g
4470:g
4465:g
4457:g
4453:g
4437:g
4427:g
4385:M
4379:M
4327:3
4322:R
4310:C
4290:3
4285:R
4261:1
4257:C
4240:C
4232:C
4225:Q
4209:4
4204:R
4192:Q
4188:T
4186:⋅
4184:Q
4180:S
4163:.
4159:}
4153:2
4150:1
4145:=
4140:2
4136:w
4132:+
4127:2
4123:z
4116:,
4111:2
4108:1
4103:=
4098:2
4094:y
4090:+
4085:2
4081:x
4072:3
4067:S
4059:)
4056:w
4053:,
4050:z
4047:,
4044:y
4041:,
4038:x
4035:(
4031:{
4027:=
4024:T
4011:T
3997:π
3993:η
3988:S
3977:π
3973:η
3969:v
3965:u
3959:η
3955:η
3951:P
3947:R
3945:(
3941:P
3937:R
3920:.
3917:)
3914:v
3905:P
3902:,
3899:u
3890:)
3887:v
3878:P
3875:+
3872:R
3869:(
3866:,
3863:u
3854:)
3851:v
3842:P
3839:+
3836:R
3833:(
3830:(
3827:=
3824:)
3821:z
3818:,
3815:y
3812:,
3809:x
3806:(
3793:3
3783:k
3779:C
3758:P
3754:R
3737:)
3734:v
3725:P
3722:,
3719:v
3710:P
3707:,
3704:u
3695:R
3692:,
3689:u
3680:R
3677:(
3674:=
3671:)
3668:w
3665:,
3662:z
3659:,
3656:y
3653:,
3650:x
3647:(
3621:y
3617:x
3613:y
3609:x
3605:y
3601:x
3599:(
3579:2
3574:Z
3568:/
3562:2
3557:R
3532:2
3527:Z
3515:L
3494:2
3489:Z
3465:2
3460:R
3448:L
3444:L
3442:/
3428:2
3423:R
3332:n
3324:n
3317:n
3297:n
3292:S
3286:/
3280:n
3275:T
3244:n
3240:)
3234:1
3229:S
3224:(
3221:=
3216:n
3211:T
3199:n
3191:n
3187:n
3183:n
3147:.
3141:2
3138:S
3136:/
3134:T
3108:n
3092:n
3087:Z
3074:-
3072:Z
3064:Z
3048:n
3043:T
3033:(
3031:H
3024:n
3020:n
3012:k
3006:n
3002:n
2994:k
2990:n
2982:n
2955:n
2950:R
2938:n
2915:n
2910:Z
2898:T
2880:G
2876:T
2864:G
2827:n
2816:n
2812:n
2796:n
2791:Z
2760:n
2755:R
2743:n
2727:n
2722:R
2698:n
2693:T
2681:n
2665:2
2660:T
2636:1
2631:S
2626:=
2621:1
2616:T
2591:.
2586:n
2574:1
2569:S
2553:1
2548:S
2539:=
2534:n
2529:T
2514:n
2510:n
2506:n
2502:n
2498:n
2488:n
2455:n
2383:.
2379:Z
2371:Z
2364:)
2359:1
2354:S
2349:(
2344:1
2333:)
2328:1
2323:S
2318:(
2313:1
2305:=
2302:)
2297:2
2292:T
2287:(
2282:1
2245:B
2217:,
2214:)
2211:1
2208:+
2205:y
2202:,
2199:x
2196:(
2190:)
2187:y
2184:,
2181:1
2178:+
2175:x
2172:(
2166:)
2163:y
2160:,
2157:x
2154:(
2130:S
2114:3
2109:R
2076:3
2071:R
2047:S
2039:S
2031:S
2023:S
2015:C
2010:S
2006:S
1980:)
1974:(
1969:)
1965:(
1951:.
1898:r
1894:θ
1890:φ
1883:φ
1879:θ
1875:R
1851:.
1846:2
1842:)
1838:q
1832:p
1829:(
1826:)
1823:q
1820:+
1817:p
1814:(
1809:2
1798:4
1795:1
1789:=
1784:2
1779:)
1774:2
1770:q
1764:p
1758:(
1752:)
1747:2
1743:q
1740:+
1737:p
1731:(
1725:2
1717:2
1714:=
1707:V
1700:,
1697:)
1694:q
1688:p
1685:(
1682:)
1679:q
1676:+
1673:p
1670:(
1665:2
1657:=
1653:)
1648:2
1644:q
1638:p
1632:(
1627:)
1622:2
1618:q
1615:+
1612:p
1606:(
1600:2
1592:4
1589:=
1582:A
1564:2
1561:/
1557:q
1553:p
1545:r
1536:2
1533:/
1529:q
1525:p
1517:R
1512:q
1508:p
1501:r
1496:R
1474:.
1469:2
1465:r
1461:R
1456:2
1448:2
1445:=
1441:)
1437:R
1431:2
1427:(
1422:)
1416:2
1412:r
1404:(
1400:=
1393:V
1386:,
1383:r
1380:R
1375:2
1367:4
1364:=
1360:)
1356:R
1350:2
1346:(
1341:)
1337:r
1331:2
1327:(
1323:=
1316:A
1266:2
1262:r
1253:2
1249:z
1245:+
1238:2
1232:)
1226:R
1216:2
1212:y
1208:+
1203:2
1199:x
1191:(
1173:r
1169:R
1162:.
1159:R
1152:r
1146:.
1143:r
1136:R
1130:.
1115:r
1111:R
1103:r
1099:R
1091:r
1087:R
1078:r
1074:R
1058:.
1054:)
1048:2
1044:y
1040:+
1035:2
1031:x
1026:(
1020:2
1016:R
1012:4
1009:=
1004:2
999:)
993:2
989:r
980:2
976:R
972:+
967:2
963:z
959:+
954:2
950:y
946:+
941:2
937:x
932:(
900:.
895:2
891:r
887:=
882:2
878:z
874:+
867:2
861:)
855:R
845:2
841:y
837:+
832:2
828:x
820:(
804:-
792:z
755:r
751:/
747:R
724:r
701:R
678:,
675:)
669:2
666:,
663:0
660:[
651:,
613:r
610:=
603:)
597:,
591:(
588:z
570:)
558:r
555:+
552:R
549:(
546:=
539:)
533:,
527:(
524:y
506:)
494:r
491:+
488:R
485:(
482:=
475:)
469:,
463:(
460:x
426:r
422:R
403:r
401:=
399:R
380:r
376:R
294:1
290:S
259:1
255:S
246:1
242:S
79:(
59:.
34:.
23:.
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.