641:
693:
190:
788:
212:
29:
358:
636:{\displaystyle {\begin{array}{lcr}{\Bigl (}1,&1,&3{\Bigr )},\\{\Bigl (}{\frac {1}{\varphi }},&{\frac {1}{\varphi ^{2}}},&2\varphi {\Bigr )},\\{\Bigl (}\varphi ,&{\frac {2}{\varphi }},&\varphi ^{2}{\Bigr )},\\{\Bigl (}\varphi ^{2},&{\frac {1}{\varphi ^{2}}},&2{\Bigr )},\\{\Bigl (}{\sqrt {5}},&1,&{\sqrt {5}}{\Bigr )}.\end{array}}}
715:
284:
would produce rectangular faces rather than squares, and the pentagram faces of the dodecadodecahedron would turn into truncated pentagrams rather than decagrams. However, it is the quasitruncation of the dodecadodecahedron, as defined by
669:
on five elements, in such a way that the three neighbors of each vertex are the three permutations formed from it by swapping the first two elements or circularly shifting (in either direction) the last four elements.
349:
1121:
304:
for the vertices of a truncated dodecadodecahedron are all the triples of numbers obtained by circular shifts and sign changes from the following points (where
1114:
1221:
1038:
999:
665:
operation on the last four elements. That is, the 120 vertices of the polyhedron may be placed in one-to-one correspondence with the 5!
165:
645:
Each of these five points has eight possible sign patterns and three possible circular shifts, giving a total of 120 different points.
1107:
1339:
1324:
1309:
1226:
915:. See especially the description as a quasitruncation on p. 411 and the photograph of a model of its skeleton in Fig. 114, Plate IV.
744:
661:
on five elements, as generated by two group members: one that swaps the first two elements of a five-tuple, and one that performs a
132:
972:(2009), "The topology of bendless three-dimensional orthogonal graph drawing", in Tollis, Ioannis G.; Patrignani, Marizio (eds.),
1354:
1329:
1314:
797:
273:), 180 edges, and 120 vertices. The central region of the polyhedron is connected to the exterior via 20 small triangular holes.
178:
114:
104:
84:
1349:
1344:
94:
1304:
863:
158:
99:
1138:
109:
89:
1334:
307:
1271:
1261:
1191:
1161:
1151:
233:
1276:
1266:
1216:
1435:
1399:
1389:
1286:
1281:
1022:
867:
1404:
1394:
824:
146:
1414:
1409:
1196:
1211:
1206:
812:
763:
293:. Coxeter et al. credit its discovery to a paper published in 1881 by Austrian mathematician Johann Pitsch.
39:
1319:
692:
189:
976:, Lecture Notes in Computer Science, vol. 5417, Heraklion, Crete: Springer-Verlag, pp. 78–89,
301:
876:
Philosophical
Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences
883:
722:
46:
1085:
787:
199:
1246:
270:
1256:
1251:
1186:
1156:
1066:
977:
899:
758:
281:
151:
241:
211:
28:
1374:
1166:
1082:
1063:
1034:
995:
1384:
1379:
1026:
1014:
987:
926:
891:
801:
1048:
911:
1130:
1044:
907:
871:
808:
773:
703:
658:
76:
887:
1238:
969:
662:
122:
363:
1429:
845:
666:
654:
352:
924:
Wenninger writes "quasitruncated dodecahedron", but this appears to be a mistake.
991:
804:
1030:
1090:
1071:
1099:
895:
221:
714:
266:
903:
262:
982:
785:
209:
1103:
959:, the truncated dodecadodecahedron appears as no. XII on p.86.
956:
286:
945:
318:
361:
310:
344:{\displaystyle \varphi ={\tfrac {1+{\sqrt {5}}}{2}}}
18:
1363:
1295:
1235:
1175:
1137:
635:
343:
621:
587:
573:
526:
512:
472:
458:
408:
394:
368:
933:, Cambridge University Press, pp. 152–153
792:3D model of a medial disdyakis triacontahedron
1115:
8:
957:Coxeter, Longuet-Higgins & Miller (1954)
287:Coxeter, Longuet-Higgins & Miller (1954)
289:. For this reason, it is also known as the
280:is somewhat misleading: truncation of the
1122:
1108:
1100:
929:(1971), "98 Quasitruncated dodecahedron",
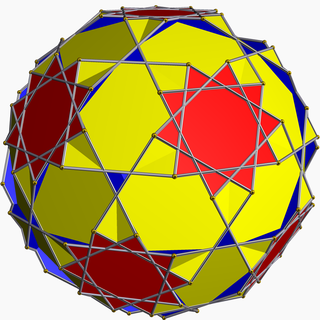
216:3D model of a truncated dodecadodecahedron
981:
653:The truncated dodecadodecahedron forms a
620:
619:
612:
592:
586:
585:
572:
571:
555:
546:
535:
525:
524:
511:
510:
504:
485:
471:
470:
457:
456:
437:
428:
413:
407:
406:
393:
392:
367:
366:
362:
360:
327:
317:
309:
682:
836:
1222:nonconvex great rhombicosidodecahedron
7:
1086:"Medial disdyakis triacontahedron"
947:Zeitschrift für das Realschulwesen
846:"59: truncated dodecadodecahedron"
230:stellatruncated dodecadodecahedron
14:
1340:great stellapentakis dodecahedron
1325:medial pentagonal hexecontahedron
1310:small stellapentakis dodecahedron
1227:great truncated icosidodecahedron
686:Medial disdyakis triacontahedron
291:quasitruncated dodecadodecahedron
1355:great pentagonal hexecontahedron
1330:medial disdyakis triacontahedron
1315:medial deltoidal hexecontahedron
798:medial disdyakis triacontahedron
713:
691:
679:Medial disdyakis triacontahedron
188:
179:Medial disdyakis triacontahedron
112:
107:
102:
97:
92:
87:
82:
27:
1350:great disdyakis triacontahedron
1345:great deltoidal hexecontahedron
1305:medial rhombic triacontahedron
1067:"Truncated dodecadodecahedron"
815:truncated dodecadodecahedron.
1:
1335:great rhombic triacontahedron
874:(1954), "Uniform polyhedra",
22:Truncated dodecadodecahedron
1272:great dodecahemidodecahedron
1262:small dodecahemidodecahedron
1202:truncated dodecadodecahedron
1192:truncated great dodecahedron
1162:great stellated dodecahedron
1152:small stellated dodecahedron
779:Truncated dodecadodecahedron
278:truncated dodecadodecahedron
234:nonconvex uniform polyhedron
226:truncated dodecadodecahedron
1277:great icosihemidodecahedron
1267:small icosihemidodecahedron
1217:truncated great icosahedron
992:10.1007/978-3-642-00219-9_9
1452:
1400:great dodecahemidodecacron
1390:small dodecahemidodecacron
1287:small dodecahemicosahedron
1282:great dodecahemicosahedron
1023:Cambridge University Press
1405:great icosihemidodecacron
1395:small icosihemidodecacron
825:List of uniform polyhedra
690:
685:
26:
21:
1415:small dodecahemicosacron
1410:great dodecahemicosacron
1197:rhombidodecadodecahedron
1131:Star-polyhedra navigator
1031:10.1017/CBO9780511569371
16:Polyhedron with 54 faces
1212:great icosidodecahedron
1207:snub dodecadodecahedron
40:Uniform star polyhedron
1366:uniform polyhedra with
1320:small rhombidodecacron
896:10.1098/rsta.1954.0003
868:Longuet-Higgins, M. S.
793:
637:
345:
217:
71:30{4}+12{10}+12{10/3}
791:
638:
346:
302:Cartesian coordinates
297:Cartesian coordinates
215:
63:= 120 (χ = −6)
1368:infinite stellations
1176:Uniform truncations
927:Wenninger, Magnus J.
739:= 54 (χ = −6)
359:
308:
261:It has 54 faces (30
1296:Duals of nonconvex
1247:tetrahemihexahedron
888:1954RSPTA.246..401C
1364:Duals of nonconvex
1257:octahemioctahedron
1252:cubohemioctahedron
1236:Nonconvex uniform
1187:dodecadodecahedron
1178:of Kepler-Poinsot
1157:great dodecahedron
1145:regular polyhedra)
1083:Weisstein, Eric W.
1064:Weisstein, Eric W.
953:: 9–24, 72–89, 216
794:
633:
631:
341:
339:
282:dodecadodecahedron
218:
1436:Uniform polyhedra
1423:
1422:
1375:tetrahemihexacron
1298:uniform polyhedra
1167:great icosahedron
1040:978-0-521-54325-5
1015:Wenninger, Magnus
1001:978-3-642-00218-2
931:Polyhedron Models
864:Coxeter, H. S. M.
784:
783:
674:Related polyhedra
649:As a Cayley graph
617:
597:
561:
493:
443:
421:
338:
332:
208:
207:
1443:
1385:octahemioctacron
1380:hexahemioctacron
1124:
1117:
1110:
1101:
1096:
1095:
1077:
1076:
1051:
1006:
1004:
985:
966:
960:
954:
942:
936:
934:
922:
916:
914:
882:(916): 401–450,
872:Miller, J. C. P.
860:
854:
853:
841:
790:
759:Index references
717:
695:
683:
642:
640:
639:
634:
632:
625:
624:
618:
613:
598:
593:
591:
590:
577:
576:
562:
560:
559:
547:
540:
539:
530:
529:
516:
515:
509:
508:
494:
486:
476:
475:
462:
461:
444:
442:
441:
429:
422:
414:
412:
411:
398:
397:
372:
371:
350:
348:
347:
342:
340:
334:
333:
328:
319:
260:
258:
257:
253:
240:. It is given a
214:
192:
147:Index references
117:
116:
115:
111:
110:
106:
105:
101:
100:
96:
95:
91:
90:
86:
85:
31:
19:
1451:
1450:
1446:
1445:
1444:
1442:
1441:
1440:
1426:
1425:
1424:
1419:
1367:
1365:
1359:
1297:
1291:
1237:
1231:
1179:
1177:
1171:
1144:
1140:
1139:Kepler-Poinsot
1133:
1128:
1081:
1080:
1062:
1061:
1058:
1041:
1013:
1010:
1009:
1002:
970:Eppstein, David
968:
967:
963:
955:. According to
944:
943:
939:
925:
923:
919:
862:
861:
857:
844:Maeder, Roman.
843:
842:
838:
833:
821:
800:is a nonconvex
786:
774:dual polyhedron
768:
752:
735:
704:Star polyhedron
681:
676:
659:symmetric group
651:
630:
629:
610:
602:
582:
581:
566:
551:
544:
531:
521:
520:
500:
498:
483:
467:
466:
448:
433:
426:
403:
402:
387:
379:
357:
356:
320:
306:
305:
299:
255:
251:
250:
248:
244:
242:Schläfli symbol
239:
210:
193:
175:Dual polyhedron
170:
163:
156:
140:
127:2 5 5/3 |
113:
108:
103:
98:
93:
88:
83:
81:
77:Coxeter diagram
59:
17:
12:
11:
5:
1449:
1447:
1439:
1438:
1428:
1427:
1421:
1420:
1418:
1417:
1412:
1407:
1402:
1397:
1392:
1387:
1382:
1377:
1371:
1369:
1361:
1360:
1358:
1357:
1352:
1347:
1342:
1337:
1332:
1327:
1322:
1317:
1312:
1307:
1301:
1299:
1293:
1292:
1290:
1289:
1284:
1279:
1274:
1269:
1264:
1259:
1254:
1249:
1243:
1241:
1233:
1232:
1230:
1229:
1224:
1219:
1214:
1209:
1204:
1199:
1194:
1189:
1183:
1181:
1173:
1172:
1170:
1169:
1164:
1159:
1154:
1148:
1146:
1135:
1134:
1129:
1127:
1126:
1119:
1112:
1104:
1098:
1097:
1078:
1057:
1056:External links
1054:
1053:
1052:
1039:
1008:
1007:
1000:
961:
937:
917:
855:
835:
834:
832:
829:
828:
827:
820:
817:
782:
781:
776:
770:
769:
766:
761:
755:
754:
750:
747:
745:Symmetry group
741:
740:
725:
719:
718:
711:
707:
706:
701:
697:
696:
688:
687:
680:
677:
675:
672:
663:circular shift
650:
647:
628:
623:
616:
611:
609:
606:
603:
601:
596:
589:
584:
583:
580:
575:
570:
567:
565:
558:
554:
550:
545:
543:
538:
534:
528:
523:
522:
519:
514:
507:
503:
499:
497:
492:
489:
484:
482:
479:
474:
469:
468:
465:
460:
455:
452:
449:
447:
440:
436:
432:
427:
425:
420:
417:
410:
405:
404:
401:
396:
391:
388:
386:
383:
380:
378:
375:
370:
365:
364:
337:
331:
326:
323:
316:
313:
298:
295:
246:
237:
236:, indexed as U
206:
205:
202:
200:Bowers acronym
196:
195:
186:
182:
181:
176:
172:
171:
168:
161:
154:
149:
143:
142:
138:
135:
133:Symmetry group
129:
128:
125:
123:Wythoff symbol
119:
118:
79:
73:
72:
69:
68:Faces by sides
65:
64:
49:
43:
42:
37:
33:
32:
24:
23:
15:
13:
10:
9:
6:
4:
3:
2:
1448:
1437:
1434:
1433:
1431:
1416:
1413:
1411:
1408:
1406:
1403:
1401:
1398:
1396:
1393:
1391:
1388:
1386:
1383:
1381:
1378:
1376:
1373:
1372:
1370:
1362:
1356:
1353:
1351:
1348:
1346:
1343:
1341:
1338:
1336:
1333:
1331:
1328:
1326:
1323:
1321:
1318:
1316:
1313:
1311:
1308:
1306:
1303:
1302:
1300:
1294:
1288:
1285:
1283:
1280:
1278:
1275:
1273:
1270:
1268:
1265:
1263:
1260:
1258:
1255:
1253:
1250:
1248:
1245:
1244:
1242:
1240:
1239:hemipolyhedra
1234:
1228:
1225:
1223:
1220:
1218:
1215:
1213:
1210:
1208:
1205:
1203:
1200:
1198:
1195:
1193:
1190:
1188:
1185:
1184:
1182:
1174:
1168:
1165:
1163:
1160:
1158:
1155:
1153:
1150:
1149:
1147:
1142:
1136:
1132:
1125:
1120:
1118:
1113:
1111:
1106:
1105:
1102:
1093:
1092:
1087:
1084:
1079:
1074:
1073:
1068:
1065:
1060:
1059:
1055:
1050:
1046:
1042:
1036:
1032:
1028:
1024:
1020:
1016:
1012:
1011:
1003:
997:
993:
989:
984:
979:
975:
974:Graph Drawing
971:
965:
962:
958:
952:
948:
941:
938:
932:
928:
921:
918:
913:
909:
905:
901:
897:
893:
889:
885:
881:
877:
873:
869:
865:
859:
856:
851:
847:
840:
837:
830:
826:
823:
822:
818:
816:
814:
810:
806:
803:
799:
789:
780:
777:
775:
772:
771:
765:
762:
760:
757:
756:
748:
746:
743:
742:
738:
733:
729:
726:
724:
721:
720:
716:
712:
709:
708:
705:
702:
699:
698:
694:
689:
684:
678:
673:
671:
668:
664:
660:
656:
648:
646:
643:
626:
614:
607:
604:
599:
594:
578:
568:
563:
556:
552:
548:
541:
536:
532:
517:
505:
501:
495:
490:
487:
480:
477:
463:
453:
450:
445:
438:
434:
430:
423:
418:
415:
399:
389:
384:
381:
376:
373:
354:
335:
329:
324:
321:
314:
311:
303:
296:
294:
292:
288:
283:
279:
274:
272:
268:
264:
243:
235:
231:
227:
223:
213:
203:
201:
198:
197:
191:
187:
185:Vertex figure
184:
183:
180:
177:
174:
173:
167:
160:
153:
150:
148:
145:
144:
136:
134:
131:
130:
126:
124:
121:
120:
80:
78:
75:
74:
70:
67:
66:
62:
57:
53:
50:
48:
45:
44:
41:
38:
35:
34:
30:
25:
20:
1201:
1089:
1070:
1018:
973:
964:
950:
946:
940:
930:
920:
879:
875:
858:
849:
839:
807:. It is the
795:
778:
736:
731:
727:
667:permutations
655:Cayley graph
652:
644:
353:golden ratio
300:
290:
277:
275:
229:
225:
219:
194:4.10/9.10/3
60:
55:
51:
1143:(nonconvex
1019:Dual Models
850:MathConsult
831:References
805:polyhedron
1180:polyhedra
1141:polyhedra
1091:MathWorld
1072:MathWorld
983:0709.4087
802:isohedral
753:, , *532
553:φ
533:φ
502:φ
491:φ
478:φ
454:φ
435:φ
419:φ
312:φ
276:The name
271:decagrams
269:, and 12
141:, , *532
1430:Category
1017:(1983),
819:See also
723:Elements
657:for the
267:decagons
222:geometry
204:Quitdid
47:Elements
1049:0730208
912:0062446
884:Bibcode
813:uniform
811:of the
730:= 120,
351:is the
263:squares
254:⁄
232:) is a
1047:
1037:
998:
910:
902:
224:, the
54:= 54,
978:arXiv
904:91532
900:JSTOR
734:= 180
265:, 12
247:0,1,2
58:= 180
1035:ISBN
996:ISBN
809:dual
796:The
710:Face
700:Type
259:,5}.
228:(or
36:Type
1027:doi
988:doi
892:doi
880:246
355:):
220:In
1432::
1088:.
1069:.
1045:MR
1043:,
1033:,
1025:,
1021:,
994:,
986:,
949:,
908:MR
906:,
898:,
890:,
878:,
870:;
866:;
848:.
767:59
764:DU
238:59
169:98
164:,
162:75
157:,
155:59
1123:e
1116:t
1109:v
1094:.
1075:.
1029::
1005:.
990::
980::
951:6
935:.
894::
886::
852:.
751:h
749:I
737:V
732:E
728:F
627:.
622:)
615:5
608:,
605:1
600:,
595:5
588:(
579:,
574:)
569:2
564:,
557:2
549:1
542:,
537:2
527:(
518:,
513:)
506:2
496:,
488:2
481:,
473:(
464:,
459:)
451:2
446:,
439:2
431:1
424:,
416:1
409:(
400:,
395:)
390:3
385:,
382:1
377:,
374:1
369:(
336:2
330:5
325:+
322:1
315:=
256:3
252:5
249:{
245:t
166:W
159:C
152:U
139:h
137:I
61:V
56:E
52:F
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.