User:NorwegianBlue/area of a square on the surface of a sphere

4499:#include <iostream> #include <math.h> &bnsp; const double PI = 3.1415926535897932384626433832795; void ErrorExit(const char* msg, int lineno) { std::cerr << msg << " program line: " << lineno << '\n'; exit(2); } // __________________________________________________ // double csc(double arg) { double s = sin(arg); if (s == 0) { ErrorExit("Division by zero attempted!", __LINE__); } return 1.0/s; } // __________________________________________________ // double pow2(double arg) { return arg*arg; } // __________________________________________________ // double g_lethe(double a) { return 0.5*csc(a)*sqrt(2.0*sqrt(2.0 + 2.0*cos(2.0*a)) - 2.0*cos(2.0*a) - 2.0); } // __________________________________________________ // double area_lethe(double a) { double G = g_lethe(a); return 2*(2*acos(G) + acos(2*pow2(G)-1)-PI); } // __________________________________________________ // double area_ksmrq(double a) { return 2*(2*acos(sqrt(cos(a)/(1.0+cos(a)))) + acos(-pow2(tan(a/2.0)))-PI); } // __________________________________________________ // int main() { std::cout << "Calculating G as a function of a" << '\n'; std::cout << "=================================\n\n"; int i; for (i = -90; i <= 540; ++i) { double a = static_cast<double>(i)*PI/180.0; // Cheating a little to avoid division by zero if (i == 0) { a += 0.0001; } else if (i == 360) { a -= 0.0001; } double G = g_lethe(a); std::cout << i << "; " << G << '\n'; } &bnsp; std::cout << "\n\n\n"; std::cout << "Calculating area of square in a unit sphere as a function of a" << '\n'; std::cout << "===============================================================\n\n"; &bnsp; for (i = 0; i <= 180; ++i) { double a = static_cast<double>(i)*PI/180.0; if (i == 0) { // Cheating a little to avoid division by zero a += 0.0001; } else if (i == 180) { // Cheating a little because of the discontinuity at 180 degrees a -= 0.0001; } double S = area_lethe(a); double T = area_ksmrq(a); std::cout << i << "; " << S << "; " << T << '\n'; } std::cout << "\n\n\n"; std::cout << "Calculating area of square with 10cm side as a function of R" << '\n'; std::cout << "=============================================================\n\n"; // for (i = 10; i < 2000; ++i) { double R = 0.1*static_cast<double>(i)/PI; double a = 10.0/R; double S = area_lethe(a)*pow2(R); std::cout << R << "; " << S << '\n'; } return 0; } 1423:

horizontal and the y-axis vertical. A grand circle is the intersection of a plane through the sphere's centre (0,0,0) with the sphere. The equation of the plane that gives rise to the grand circle whose arc segment gives the top side of the "square" is y = tan(a/2) × z = tz (think of it as looking sideways along the x-axis). At the top right corner of the "square" we have x = y. Solving these three equations (sphere, plane, x = y) for z, using z > 0, gives us z = 1 / sqrt(1+2t). Now if c is the angle between the rays from the centre of the sphere to this corner and its opposite (which, if R = 1, is also the length of the diagonal), so c/2 is the angle between one of these rays and the one through (0,0,1), then z = cos(c/2). Combining this with the other equation for z gives the result cos(c/2) = 1 / sqrt(1+2t). Although I did not work out the details, I think you can combine this with

615:

are working on the surface of a sphere. We have two pairs of great circles. The angle between the first pair of great circles, expressed in radians, is 10cm/r, where r is the radius of the sphere. The angle between the second pair of great circles is equal to the angle between the first pair. The plane defined by the axes corresponding to the first pair of great circles is perpendicular to the plane defined by the axes corresponding to the second pair of great circles. At two opposite locations on the surface of the sphere, "squares" are formed, as illustrated in the image. Is it possible to express the area of one of these "squares" analytically, such that the area tends to 100cm as r tends to infinity? --

2481:. We are told that the actual distance on the sphere is exactly 10 cm, but we are not told the sphere radius. The appearance of the "square" depends a great deal on the radius, and so does its area. When the radius is smaller, the sides "bulge out" to enclose more area, the corner angles are greater, and the sphere bulges as well. As the sphere radius grows extremely large, the square takes up a negligible portion of the surface, the sides become straighter, the angles approach perfect right angles, and the sphere bulges little inside the square. 2170:

luxury of stipulating 90° angles. Food for thought: Is such a figure always possible, even on a small sphere? (Suppose the equatorial circumference of the sphere is itself less than 10 cm; what then?) Even if it happens that we can draw such a figure, is it clear what we mean by its area? Or would we prefer to stipulate a sufficiently large sphere? (If so, how large is large enough?) Figures can be a wonderful source of inspiration and insight, but we must use them with a little care. --

177:

be (I think sqrt(50)) before the sphere 'fall' through the square it will be around maybe 150-200 square cm. But again you do not want 'simple' answers, to get a real answer you need to give more info. I guess what you want is not a answer, but a formula f(r,s)=..... where r is the radius of the sphere and s is the side of the 'square' and the result is the area of the 'square'. But sorry I will not even try to do that math. :-) (maybe I should learn wikipedia math symbols instead ....)

2492:

third point is a quarter of the way around the equator (latitude 0°, longitude 90°). This triangle has three perfect right angles for a total of 270° (or 3π/2), and encloses exactly one octant — one eighth of the surface area — of the sphere. The total surface area is 4π, so the triangle area is π/2. This area value is exactly the same as the excess of the angle sum, 3π/2, compared to a flat right triangle, π. The simple rule is, this is true for

4227:, where a quantity inside a square root goes negative.) Both algebra and geometry are telling us we cannot step carelessly into the domain of small radii. Try to imagine what shape the "square" may take when the circumference of the sphere is exactly 10 cm; both ends of each edge are the same point! Not only do we not know the shape, we do not know what to name and measure as the "inside" of the square. 603:

to be a square joining its four vertices (aligned diagonal to the coordinate axes), plus four vaguely lens-shape pieces. The area of each of the lens-shape pieces is obtained by considering drawing straight lines connecting its two vertices to the opposite corner (i.e. to the center of the arc): it's the area of the sector of the circle minus the area of the triangle. Hope this makes some kind of sense.

900: 2422:, and which passes through the centre of the sphere. As previously stated, I have little mathematical training. I therefore made a physical model by drawing on the surface of a ball, before making the first image. I convinced myself that such a plane is well-defined, and that this length of arc on a unit sphere would be identical to the angle between P 192:, a hemispere would be a valid "squareon a sphere" with side length = 0.25*sphere circumference and area=0.5*sphere area. Indeed presumably a hemisphere is an instance of every regular polygon with the same area and side length = 1/N * circumference. I note that this is a "valid" (?) 2 sided polygon and even a valid (?) one sided polygon! -- 4241:, we must include the restriction of the kind of geometry in which it applies. When we integrate a partial differential equation, the boundary conditions are as important as the equation itself. It is all too easy to fall into the careless habit of forgetting the relevance of limitations, but we do so at our peril. -- 3794: 3588: 3844:

Unsurprisingly, the function behaves weirdly below the smallest reasonable value of R, but from R ˜ 6.366 cm and onwards, the function behaves as predicted, falling rapidly from 254.65 cm, and approaching 100 cm asymptotically. In case anybody is interested in the calculations, I have put the program

3822:

Finally, I would like to address the question of the orignial anonymous user who first posted this question on the science desk. Let us see how the area of the square behaves as R increases, using 10 cm for the length of arc in each side of the "square". The smallest "reasonable" value of R is 20cm/p

2491:

follows a powerful and surprisingly simple rule, based on the idea of angular excess. Consider a triangle drawn on a unit sphere, where the first point is at the North Pole (latitude 90°, longitude irrelevant), the second point drops straight down onto the equator (latitude 0°, longitude 0°), and the

2195:

What is meant by "the angle between the … circles"? That's not really the same as the arclength of a side as depicted. Also note that the orginal post suggests that the side might be a quarter of a circle. If that is true, then the "square" is actually a great circle! Each angle will be 180°, and the

2181:

The red circles are supposed to be two pairs of great circles. The angle between the first pair of great circles, expressed in radians, is 10cm/R, where R is the radius of the sphere. The angle between the second pair of great circles is equal to the angle between the first pair. The plane defined by

878:

135:

If you are asking how to find the area of some shape on a sphere, then perhaps we can give you a helpful answer - but in order to do so, you have todefine the shape 'exactly'. For example we could start analysing the area of a square projected onto the surface of a sphere. This isn't a square, it has

624:

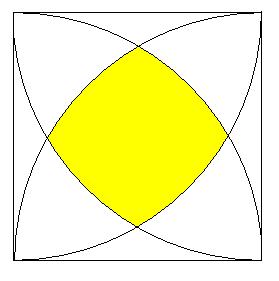
I love math problems that have multiple approaches. I'll wave my hands a bit and assert that the corners of the yellow area cut the arcs in thirds. Call A the yellow corner on the left, and B the one on top. Construct segment AB. Figure out the area between segment AB and arc AB, and add four of 'em

2507:

Thus we simplify our area calculation by two strategies. First, we divide out the effect of the radius so that we can work on a unit sphere. Second, we split the "square" into two equal halves, two equilateral triangles, by drawing its diagonal. Of course, once we find the triangle's angular excess

815:

Yes it is a solid angle of a sphere type question - the missing info. is the radius r of the sphere - without that answers will need to be functions of r. By the way if the interior angles of a triangle drawn on a sphere are a,b and c then the solid angle covered by the triangle (spherical geometry

602:

There's certainly a way to avoid calculus. It's easy enough to get the cartesian coordinates of the four vertices of the yellow area. (e.g. the top one is at (1/2, sqrt(3)/2) just because it makes an equilateral triangle with the bottom two vertices of the main square.) Then take the yellow area

286:

As you just want to know how to do it, I will not carry out actual calculations. Call A, B, C, D the vertices of the square in a clockwise fashion starting from the bottom left one. Let E be the top point of intersection between the four circumferences, and let F be the right one. Then one can show

176:

A little bit more complicated answer, as I see it this can not be answered with the data you have given, the answer depends on the radius of the sphere. If the radius of the sphere is 'close' to infinity the area will be very close to 100 square cm, if the radius of the sphere is as small as it can

614:

Like the person posing the question, I am not a mathematician. I suspect that the responses so far have not given enough practical detail to be helpful to the questioner. Based on the original question, and on this repost, I'll have a go at reformulating what I think the questioner had in mind: We

1414:

I'm afraid I didn't understand (I'm not a mathematician :-) ). If we let (uppercase) C be the "right" (i.e. 90°+something) angle in the triangle in the second figure, and (lowercase) c be the diagonal that we are trying to calculate, could you please show the steps leading to this result (or

4236:

delimited by their range of applicability. Every function has a stated domain; every theorem has preconditions; every proof depends on specific axioms and rules of inference. Once upon a time, we manipulated every series with freedom, with no regard to convergence; to our chagrin, that sometimes

1422:

For simplicity, let's put R = 1, since you can divide all lengths first by R, and multiply the area afterwards by R. Then the equation of the sphere is x + y + z = 1. Take the point nearest to the spectator in the first image to be (x,y,z) = (0,0,1), so z decreases when receding. Take the x-axis

2169:

Despite the figure, which is only suggestive (and not quite correct), are we agreed on the definition of a "square on a sphere"? The question stipulates equal side lengths of 10 cm. To avoid a rhombus we should also stipulate equal interior angles at the vertices, though we do not have the

763:, and the preceding answer appears to be plane geometry (correct me if I'm wrong!). I think we can be reasonably sure that this is not a homework question, because of the vague way in which it was formulated. I believe what the questioner had in mind was the area illustrated in yellow here: 250:

Yes user:grutness is sort of right - but what is missing is the radius of the sphere otherwise answers will have to be expressed as a function of radius. Take the solid angle created by half the 'square' ie a spherical triangle - double it and multiply by r squared to get the surface area.

2461:. The problem arises when we cut with a third plane. If we cut near where the two planes intersect we get a short arc; if we cut far from their intersection we get a longer arc. In other words, the dihedral angle between the two planes does not determine the arclength of the "square" side. 2542:

What if we perform a simple coordinate transform to spherical coordinates and perform a 2-dimensional integral in phi and theta (constant r = R). Then, dA = r^2*sin(theta)*dphi*dtheta, and simply set the bounds of phi and theta sufficient to make the lengths of each side 10 cm.

154:

You will have to express the sides of the "square" mathmatically to determine the boundaries of the double integral that will give you the area. You will probably want to solve it in spherical coordinates. You are going to have to know some calculus for this one.

873: 2152: 2511:

Notice that this mental model assumes the sphere radius is "large enough", so that at worst the square becomes a circumference. We still have not considered what we should do if the sphere is smaller than that. It seems wise to ignore such challenges for now.

1347: 2561:. Armed with a table of trigonometric identities, I went carefully through the calculations, and am happy to report that I feel that I understood every single step. I was not able to simplify the last expression much further, the best I can come up with is 1069:

The natural way I suspect the question should presumably be answered is to take the square on the flat plane and use Jacobians to transform it onto the sphere. Those with a firmer grip of analysis would probably want to fill in the details at this point...

4211: 3346: 4237:

produced nonsense results. Once it was supposed that every geometry was Euclidean, and that every number of interest was at worst a ratio of whole numbers; we now make regular use of spherical geometry and complex numbers. When we state the

736: 3189: 1846: 3594: 4078: 1019: 4389: 2671: 3388: 2464:

Instead, use the fact that any two distinct points which are not opposite each other on the sphere determine a unique shortest great circle arc between them, lying in the plane containing the two points and the center. Our value

4839: 1061:. I would appreciate if somebody told me if I am on the right track, and, if so, how to complete the calculations. If my presentation of the problem reveals that I have misunderstood some of the theory, please explain. -- 778:

Is anybody able to come up with a formula for the yellow area in terms of r, the radius of the sphere? Also, it would be nice if the person that posed the question confirmed that this is what he/she is looking for.

1546: 3369:

mentions above, i.e. to a hemisphere, and the area, 2p is correct. in the interval [90°..180°), the function returns the smaller of the two areas. I also notice that the function looks suspiciously elliptical.

1024:

I then attempted to divide the square into two triangles, and compute the area of one of these, but am stuck because I don't know the diagonal. Since this is spherical geometry, I doubt that it is as simple as

514: 1713: 3032: 1448:

As vibo correctly points out above, the square will not have right angles, so my calculation is not correct. Here is my new calculation. Assuming all angles of the square are equal, label this angle

5238: 909:

which states that the area of a triangle on a sphere is (A + B + C - p) × R, where A, B and C are the angles between the sides of the triangle, as illustrated in the second drawing. I also found the

3970: 4590: 2270: 5035: 2000: 277:

This is the problem. It's not a homework question and I just need to know how to work it out. Length of the square is 10 cm, find the shaded area (the curved lines are the loci of the 4 corners)

145:

BTW, did you know that an equilateral "triangle" on a sphere touching the points lat=0,long=0; lat=0,long=90; lat=90,long=any has three 90 degree corners and has an area of 1/8 of the sphere? --

4945: 2925: 1929: 4670: 2350: 1083:

with four right angles and two sides of length 5. The cut the squares along x+z=0, x-z=0 giving eight triangles, each with one 45 degree angles, one right angle and one side of length 5. --

2023: 855:

This question was originally posted in the science section, but belongs here. The original questioner has stated clearly that it is not a homework question. It was formulated as follows:

1233: 5100: 4475: 1607: 1399:

I got the following for the diagonal angle c of the big square from "first principles" (just analytic geometry in 3D): cos(c/2) = 1 / sqrt(1+2t), where a = 10cm/R and t = tan(a/2). --

861:"How do one find the area of a square drawn on a sphere? A square with the side of 10 cm, and draw loci (10cm) on each corners (quarter of a circle in a square to give the "square")" 1059: 4223:

For the arccosine to be defined, its argument must be between -1 and +1, and this fails when the radius goes below the stated limit. (A similar problem occurs with the formula for

2734: 2157:

I'm pretty sure this can be simplified quite a bit, but the simplification I got doesn't agree with the one Mathematica told me. Anyway, the expansion also has the right limit of

4088: 3195: 2840: 419: 373: 2196:

area "enclosed" will be a hemisphere of a sphere with radius 20 cm/π, namely 2π(20 cm/π) = 800 cm/π, approximately 254.65 cm.

4433: 2791: 169:

This is NOT a homework question, i just want a head start of what to do. If you do not understand what i said, tell me and i'll create an image from Paint. many thanks!

632: 3789:{\displaystyle area_{square}=2\times \left(2\cos ^{-1}\left({\sqrt {\frac {\cos a}{1+\cos a}}}\,\right)+\cos ^{-1}(-\tan ^{2}{\frac {a}{2}})-\pi \right)\times R^{2}\!} 3038: 173:

I do not understand! OK one more 'simple' answer to your to 'simple' question, between a very very very small bit more than 100 square cm to about maybe 200 square cm.

1732: 1179:= p/2? This is spherical geometry, and the four "right" angles in the "square" in the first drawing add up to more than 2p, don't they, or am I missing something? -- 341: 313: 2555:

Thanks a million to the users who have put a lot of work in explaining this to me, and in showing me the calculations necessary. I started out based on the work of

3976: 3583:{\displaystyle area_{triangle}=\left(2\cos ^{-1}\left({\sqrt {\frac {\cos a}{1+\cos a}}}\,\right)+\cos ^{-1}(-\tan ^{2}{\frac {a}{2}})-\pi \right)\times R^{2}\!} 920: 4285: 2567: 4398:

only, which is a known constant when the radius and length of arc are given (a=10cm/R for the example that prompted my follow-up question), I will substitute

2182:

the axes corresponding to the first pair of great circles is perpendicular to the plane defined by the axes corresponding to the second pair of great circles.

879:

the axes corresponding to the first pair of great circles is perpendicular to the plane defined by the axes corresponding to the second pair of great circles.

524:

That's quite funny. There's a much easier way to figure this out. I won't give the details just in case it is homework, but the approach looks like this: let

894:

I am not a mathematician, but felt that it "ought to" be possible to express this area in terms of R, and decided to try to find the necessary information.

4279:

provided the following function for cos A, where A=B represents half of the "right" (i.e. 90°+something) angle C in a "square" on the surface of a sphere.

2410:

in which the second great circle lies. The arc length depicted was intended to represent the intersection between the surface of the sphere, and a plane P

3839: 1079:

An easier way to tackle this might be to exploit the symetry of the situation. Slice the sphere into 4 along z=0 and x=0. This will give four identical

4735: 4435:

for the r.h.s. Note that the function is undefined at a=0°±180° because of the sine function in the denominator. The graph of g(a) looks like this:

3360: 4438: 2793:

for the r.h.s. Note that the function is undefined at a=0°±180° because of the sine function in the denominator. There is a graph of g(a) on my

1474: 839: 769: 424: 4232:

This raises an important general point about the teaching, understanding, and application of mathematics. Statements in mathematics are

2188:

resolve the ambiguity with respect to the rhombus, provided that the area of the square is less than half of the area of the sphere? --

867:

Based on the discussion that followed, I think what the questioner had in mind is the area illustrated in yellow in the drawing below:

1618: 568:

Your method doesn't account for all the areas. In addition to "a" and "b" there are is also the pointy area between two "b" areas.

226:. So, find the area of a right-angled triangle (or sphere-surfaced equivalent) with shorter sides both length 10cm, and double it. 3827:

points out. Driven by curiosity, I will start plotting the function at lower values than the smallest reasonable one (in spite of

823:

My question, and possibly the original poster's question, was if somebody could provide a formula for the area, in terms of r. --

793:. I ignored the sphere thing, for some reason or another. But isn't there insufficient information to calculate this? (Is this a 260: 2936: 2756:

only, which is a known constant when the radius and length of arc are given (a=10cm/R for the given example), let us substitute

315:. Hence, if you set up Cartesian cohordinates so that A=(0,0), B=(0,1), C=(1,1) and D=(1,0), the x-cohordinate of F is just sin( 280: 81: 5139: 2457:

does, indeed, lie in a well-defined plane through the center of the sphere. Between two such planes we do have a well-defined

3918: 2469:

is the angle between the two points, as measured at the center of the sphere. Were we to pick two opposite points, we'd have

1201:. I can solve this triangle as well, but it's quite a bit messier. Lemme see if I can clean it up, and then I'll post it. - 166:

A square with the side of 10 cm, and draw loci (10cm) on each corners (quarter of a circle in a square to give the "square")

4524: 2204: 532:

be the area of one of the four curvy arrowhead-like shapes in the corners. Express the area of the whole square in terms of

4964: 1940: 4870: 2846: 1857: 4617: 2297: 2147:{\displaystyle A=\cos ^{-1}\left({\frac {1}{2}}{\sqrt {1-\left(-1+{\sqrt {2+2\cos 2a}}\right)^{2}}}\csc a\right).\,\!} 287:

that the segments AE subtends pi/6and AF divide the right angle BAD into three equal angles, each of them measuring

1342:{\displaystyle 2R^{2}\left(2\sin ^{-1}\left({\frac {\sin a}{\sqrt {1-\cos ^{4}a}}}\right)-{\frac {\pi }{2}}\right)} 3365:

Seems reasonable up to 90°. The value at 90° corresponds to the "square" with four corners on a great circle that

77:

Well there's a way to do triangles (it's in my friends multivariable calculus book), but I dunno about squares. --

2508:

we must remember to double the value (undoing the split) and scale up by the squared radius (undoing the shrink).

114:

as in an object with 4 sides, and their interior angle does not add up to 360 degrees. HOw do you find the area?

5050: 4446: 1557: 224:

Well there's a way to do triangles (it's in my friends multivariable calculus book), but I dunno about squares

4206:{\displaystyle {}=\left(4\cos ^{-1}(-\tan ^{2}{\frac {10\ \mathrm {cm} }{2R}})-2\pi \right)\times R^{2}.\,\!} 2177:

The figure was drawn by hand, and is obviously not quite correct, but doesn't the accompanying description:

1364:

as the curvature goes to zero. From the series, I can say that to leading two orders of correction, area =

1096:

I think vibo is on the right track. You can use the law of sines to calculate the length of the diagonal. -

1028: 604: 3838: 2682: 2519:

Thank you. I really appreciate your taking the time to explain this to me which such detail and clarity. --

54:

It might be better to say that a sphere is a surface (a two dimensional Riemannian manifold) with constant

2485: 910: 569: 252: 86: 78: 3341:{\displaystyle area_{square}=2\times \left(2\cos ^{-1}G+\cos ^{-1}(2G^{2}-1)-\pi \right)\times R^{2}\!} 1415:

rephrase it, if I misinterpreted your choice of which of the angles A,B,C that was the "right" one)? --

1186:

You may be right, I cannot assume that the angles are right angles. Let me mull it over some more. -

1088: 2473: = π, which is half the equatorial circumference of a unit sphere. For a sphere of radius 4238: 3359: 2808: 913:

which relates the angles A, B and C to the angles a, b and c which define the sides of the triangle

517: 378: 346: 731:{\displaystyle (2R\sin {\frac {\pi }{12}})^{2}+(2R^{2}({\frac {\pi }{6}}-\sin {\frac {\pi }{6}}))} 4257: 3854: 3184:{\displaystyle area_{triangle}=\left(2\cos ^{-1}G+\cos ^{-1}(2G^{2}-1)-\pi \right)\times R^{2}\!} 2520: 2431: 2189: 1416: 1180: 1062: 843: 824: 801: 780: 751: 616: 232: 216: 212: 17: 4437: 4401: 2759: 3861:

Well done. It does appear that you overlooked my simple formula for the area, which depends on

1841:{\displaystyle \cos c=\cos ^{2}+\sin ^{2}a\left({\frac {\sin ^{2}c}{2\sin ^{2}a}}-1\right)\,\!} 4715: 1431: 1403: 790: 189: 121: 318: 290: 4073:{\displaystyle {}=\left(4\cos ^{-1}(-\tan ^{2}{\frac {a}{2}})-2\pi \right)\times R^{2}\,\!} 1427:'s "cut in eight" approach and the sines' law to figure out the missing angle and sides. -- 1014:{\displaystyle {\frac {\sin a}{\sin A}}={\frac {\sin b}{\sin B}}={\frac {\sin c}{\sin C}}.} 4384:{\displaystyle \cos A={\frac {1}{2}}\csc a{\sqrt {2{\sqrt {2+2\cos 2a}}-2\cos 2a-2}}\,.\!} 2666:{\displaystyle \cos A={\frac {1}{2}}\csc a{\sqrt {2{\sqrt {2+2\cos 2a}}-2\cos 2a-2}}\,.\!} 1424: 1084: 2484:

We do not have a handy rule for the area of a square on a sphere. Luckily, the area of a

242:

Grutness, You are missing something. On a sphere triangles etc don't scale like that. --

872: 789:

Oh, it doesn't matter what they're looking for -- this is fun! Probably belongs over in

768: 4722:, noting that we have an equilateral triangle so the first term vanishes. Thus, noting 4276: 3802: 2741: 2557: 2458: 2162: 1385: 1360:

And now I'm here to tell you that Mathematica assures me that this function approaches

1354: 1202: 1187: 1172: 1151: 1112: 1097: 1071: 884:

The question is how to express the yellow area in terms of R, the radius of the sphere.

2402:

By "the angles between a pair of great circles", I meant the angle between the plane P

104:

So.. why don't you just divide that square in two triangles .. and add up the results?

4248:

Yes, I did overlook the (now painfully obvious) fact that the sum of the angles was 2

1452:. Then draw the diagonal, and the resulting triangle will be equilateral with sides 798: 773: 748: 593: 561: 243: 227: 193: 146: 137: 741: 2454: 1428: 1400: 817: 263: 163:

actually, the whole thing goes like this, i am tryin' the find the area of this...

125: 63: 899: 58:

curvature, while the plane is a surface (two dimensional manifold) with constant

794: 256: 178: 44: 4834:{\displaystyle \mathrm {haversin} \ c=\sin ^{2}a\,\mathrm {haversin} \ 2A,\,\!} 3823:˜ 6.366 cm, which should lead to a surface area of approximately 254.65 cm, as 5042: 4242: 3890: 3828: 3824: 3812: 3806: 3378: 3366: 2544: 2513: 2384: 2171: 204: 156: 2375:

The original question was about the area, so we should conclude with that: (4

740:

but that's only because I looked up the formulas for the circular segment on

203:

I don't get this. Perhaps drawing that picture would help clear things up. --

5244:

No doubt a cleaner way to this simple solution exists, but this may suffice.

222:

Excuse me if I'm missing something obvious here, but M1ss1ontomars2k4 says:

5110:

using the fundamental trigonometric identity, and eliminate both sin

279: 906: 747:

Signed, math degree 30 years ago next month and am rusty as all hell. --

4252:. Your final point is well taken. I understood that the reason for the 3351:

I calculated the behaviour of this area function on a unit sphere when

2802:

We can now calculate the area of the triangle, and that of the square.

4256:'s was a domain error, but thanks for pointing out the exact spots. -- 1541:{\displaystyle {\frac {\sin a}{\sin A}}={\frac {\sin c}{\sin 2A}}\,\!} 40: 36: 4493:

Here is the program that was used for the calculations referred to:

1353:

For the square. Now I just have to see whether this answer works. -

625:

to a square of side AB. I think the result will look something like

509:{\displaystyle 4\int _{1/2}^{{\sqrt {3}}/2}{\sqrt {1-x^{2}}}-1/2dx} 2430:. Please correct me if I am mistaken, or confirm if I am right. -- 4604:), the side length as an angle. The angle of interest is really 1708:{\displaystyle \cos c=\cos ^{2}a+\sin ^{2}a(2\cos ^{2}A-1).\,\!} 2284:, the side length as an angle. The angle of interest is really 4253: 3816: 3372:

Are we computing a much simpler function in a roundabout way?

261:

Knowledge:Reference desk/Science#(continued) Area on a sphere

3799:

I computed the area, and found that in the range (0°..90°],

898: 871: 2496:

triangle on a unit sphere. If instead the sphere radius is

1126:

From which I get using the spherical law of sines that sin

576:

Yes, you're quite right. So call the thin area at the side

3027:{\displaystyle area_{triangle}=(A+B+C-\pi )\times R^{2}\!} 5233:{\displaystyle (y^{2}-1)x^{2}+(-2y^{2})x+(y^{2})=0.\,\!} 375:. The equation of the circumference centered in A being 31:

how do one find the area of a square drawn on a sphere?

3965:{\displaystyle \mathrm {area} _{\mathrm {square} }\,\!} 3865:

alone. Recall that when the square is split, the angle

4585:{\displaystyle \cos ^{2}A={\frac {\cos a}{1+\cos a}},} 3811:, within machine precision. Above 90°, the formula of 2265:{\displaystyle \cos ^{2}A={\frac {\cos a}{1+\cos a}},} 1150:= p/2, so I have the triangle, and hence the square. - 5142: 5053: 5030:{\displaystyle \cos c=1-2\sin ^{2}A\,\sin ^{2}a.\,\!} 4967: 4873: 4738: 4620: 4527: 4449: 4404: 4288: 4091: 3979: 3921: 3597: 3391: 3198: 3041: 2939: 2849: 2811: 2762: 2685: 2570: 2406:

in which the first great circle lies, and the plane P

2300: 2207: 2026: 1995:{\displaystyle \cos c=-1\pm {\sqrt {2+2\cos 2a}}\,\!} 1943: 1860: 1735: 1621: 1560: 1477: 1236: 1031: 923: 635: 427: 381: 349: 321: 293: 4940:{\displaystyle 1-\cos c=(1-\cos 2A)\sin ^{2}a,\,\!} 2920:{\displaystyle \cos 2A=2\cos ^{2}A-1=2G^{2}-1\,.\!} 2795: 886:Obviously, as R ? 8, the area ? 100 cm. 540:. Express the area of a quarter circle in terms of 5232: 5094: 5029: 4939: 4833: 4664: 4584: 4469: 4427: 4383: 4205: 4072: 3964: 3788: 3582: 3340: 3183: 3026: 2919: 2834: 2785: 2740:here, it simplifies this expression quite a bit. - 2728: 2665: 2344: 2264: 2146: 1994: 1924:{\displaystyle \cos ^{2}c+2\cos c-1=2\cos 2a.\,\!} 1923: 1840: 1707: 1601: 1540: 1341: 1053: 1013: 730: 508: 413: 367: 335: 307: 5229: 5091: 5026: 4936: 4830: 4424: 4380: 4202: 4069: 3961: 3785: 3579: 3337: 3180: 3023: 2916: 2831: 2782: 2662: 2143: 1991: 1920: 1837: 1704: 1598: 1537: 1193:OK, I think the right assumption to make is that 759:The question was related to the area of a square 43:is 3D, so you can not draw a square on a sphere. 4714:The idea of the derivation is to start with the 4665:{\displaystyle \cos C=-\tan ^{2}{\frac {a}{2}}.} 2345:{\displaystyle \cos C=-\tan ^{2}{\frac {a}{2}}.} 1103:The law of cosines for spherical trig gives cos 3893:'s results as well, where we may use simply 4 3831:advice to "ignore such challenges for now"). 2677:You should probably make use of the identity 8: 4519:By a series of manipulations I came up with 2930:According to Girard's formula, we then have 2199:By a series of manipulations I came up with 5118:as well. We obtain a quadratic equation in 2017:, I am in a position to solve the triangle 548:. This gives you simultaneous equations in 4684: = π; while for the limit case, 2364: = π; while for the limit case, 5228: 5213: 5191: 5169: 5150: 5141: 5095:{\displaystyle \sin c=2\cos A\sin a.\,\!} 5090: 5052: 5025: 5010: 5005: 4993: 4966: 4935: 4920: 4872: 4829: 4791: 4790: 4778: 4739: 4737: 4649: 4640: 4619: 4547: 4532: 4526: 4470:{\displaystyle {\frac {1}{2}}{\sqrt {2}}} 4460: 4450: 4448: 4423: 4403: 4376: 4325: 4320: 4301: 4287: 4201: 4192: 4149: 4140: 4131: 4109: 4092: 4090: 4068: 4062: 4028: 4019: 3997: 3980: 3978: 3960: 3938: 3937: 3923: 3920: 3779: 3748: 3739: 3717: 3704: 3670: 3653: 3611: 3596: 3573: 3542: 3533: 3511: 3498: 3464: 3447: 3405: 3390: 3331: 3298: 3276: 3254: 3212: 3197: 3174: 3141: 3119: 3097: 3055: 3040: 3017: 2953: 2938: 2912: 2900: 2872: 2848: 2830: 2810: 2781: 2761: 2708: 2684: 2658: 2607: 2602: 2583: 2569: 2329: 2320: 2299: 2227: 2212: 2206: 2142: 2117: 2087: 2064: 2054: 2037: 2025: 1990: 1965: 1942: 1919: 1865: 1859: 1836: 1810: 1789: 1782: 1765: 1752: 1734: 1703: 1679: 1657: 1638: 1620: 1602:{\displaystyle \sin c=2\cos A\sin a.\,\!} 1597: 1559: 1536: 1507: 1478: 1476: 1324: 1302: 1278: 1262: 1244: 1235: 1032: 1030: 982: 953: 924: 922: 772:The red curves are supposed to represent 712: 693: 684: 665: 651: 634: 580:and make three simultaneous equations in 492: 478: 466: 456: 449: 448: 439: 435: 426: 399: 386: 380: 357: 350: 348: 325: 320: 297: 292: 3376:I next studied how the formula given by 1851:which reduces to the quadratic equation 4510:Info from KSmrq which was commented out 911:law of sines for triangles on a sphere, 1054:{\displaystyle {\sqrt {2}}\times 10cm} 528:be the area coloured yellow area, and 2729:{\displaystyle \cos 2a=2\cos ^{2}a-1} 516:(using symmetry to simplify things). 7: 1612:From the law of cosines I have that 136:curved edges. So back to you... -- 27:Initial presentation of the problem 4813: 4810: 4807: 4804: 4801: 4798: 4795: 4792: 4761: 4758: 4755: 4752: 4749: 4746: 4743: 4740: 4153: 4150: 3954: 3951: 3948: 3945: 3942: 3939: 3933: 3930: 3927: 3924: 421:, the area you are looking for is 24: 4481:approaches 180°, as well as when 4443:The function appears to approach 3847: 816:here) is a+b+c-pi in steradians. 4436: 3837: 3358: 767: 278: 556:which you can easily solve for 5219: 5206: 5197: 5178: 5162: 5143: 4913: 4892: 4420: 4414: 4168: 4121: 4038: 4009: 3889:. This observation applies to 3873:, so the sum of the angles is 3758: 3729: 3552: 3523: 3310: 3288: 3153: 3131: 3007: 2983: 2778: 2772: 2477:, the circumference is 2π 1697: 1669: 725: 722: 690: 674: 662: 636: 1: 4394:Since the r.h.s. is based on 3355:is in the range (0°...180°): 2835:{\displaystyle \cos A=G.\,\!} 2752:Since the r.h.s. is based on 1718:My goal here is to eliminate 1468:. The law of sines tells me 414:{\displaystyle x^{2}+y^{2}=1} 368:{\displaystyle {\sqrt {3}}/2} 3815:leads to numerical problems 802:∇∆∇∆ 752:∇∆∇∆ 2500:, the area is multipled by 1228:This makes my final answer 273:Followup on science section 259:- see continued talk below 35:Simple answer, you cant, a 5266: 4680: = π/2 produces 4485:approaches 0° from above. 4428:{\displaystyle G=g(a)\,\!} 4272:Graph of the function g(a) 2786:{\displaystyle G=g(a)\,\!} 2414:, which is orthogonal to P 2360: = π/2 produces 1722:. First I substitute cos 1091:) 15:44, 28 May 2006 (UTC) 761:on the surface of a sphere 4845:or, noting haversin 4676:For the hemisphere case, 4245:02:36, 30 May 2006 (UTC) 3857:23:54, 29 May 2006 (UTC) 2547:18:11, 31 May 2006 (UTC) 2516:21:23, 29 May 2006 (UTC) 2356:For the hemisphere case, 2192:21:51, 28 May 2006 (UTC) 2174:20:40, 28 May 2006 (UTC) 2165:20:16, 28 May 2006 (UTC) 1419:18:07, 28 May 2006 (UTC) 1357:16:14, 28 May 2006 (UTC) 1190:16:58, 28 May 2006 (UTC) 1183:16:49, 28 May 2006 (UTC) 1100:15:44, 28 May 2006 (UTC) 1065:14:11, 28 May 2006 (UTC) 851:Followup on maths section 820:16:32, 27 May 2006 (UTC) 783:09:19, 27 May 2006 (UTC) 596:15:55, 26 May 2006 (UTC) 564:15:33, 26 May 2006 (UTC) 266:16:42, 27 May 2006 (UTC) 238:05:46, 25 May 2006 (UTC) 219:20:58, 24 May 2006 (UTC) 4260:19:40, 30 May 2006 (UTC) 3853:Again, thank you all. -- 2744:02:01, 30 May 2006 (UTC) 2523:23:34, 29 May 2006 (UTC) 2434:20:19, 29 May 2006 (UTC) 2387:04:43, 29 May 2006 (UTC) 1435:19:59, 28 May 2006 (UTC) 1407:16:02, 28 May 2006 (UTC) 1388:16:25, 28 May 2006 (UTC) 1205:17:20, 28 May 2006 (UTC) 1154:16:11, 28 May 2006 (UTC) 1115:16:06, 28 May 2006 (UTC) 1074:15:28, 28 May 2006 (UTC) 846:14:32, 28 May 2006 (UTC) 842:in the maths section. -- 827:16:43, 27 May 2006 (UTC) 804:16:13, 27 May 2006 (UTC) 754:05:41, 27 May 2006 (UTC) 619:21:26, 26 May 2006 (UTC) 607:20:56, 26 May 2006 (UTC) 572:15:37, 26 May 2006 (UTC) 520:14:48, 26 May 2006 (UTC) 246:11:59, 25 May 2006 (UTC) 207:08:33, 25 May 2006 (UTC) 196:16:12, 24 May 2006 (UTC) 181:14:33, 24 May 2006 (UTC) 159:11:11, 24 May 2006 (UTC) 149:10:25, 24 May 2006 (UTC) 140:10:25, 24 May 2006 (UTC) 128:10:03, 24 May 2006 (UTC) 89:03:48, 25 May 2006 (UTC) 66:10:03, 24 May 2006 (UTC) 47:09:38, 24 May 2006 (UTC) 3809:yield identical results 1175:: How can you say that 5234: 5096: 5031: 4941: 4835: 4666: 4600:is 10 cm/(2π 4586: 4471: 4429: 4385: 4267:Supplementary material 4207: 4074: 3966: 3790: 3584: 3342: 3185: 3028: 2921: 2836: 2787: 2730: 2667: 2346: 2266: 2148: 1996: 1925: 1842: 1709: 1603: 1542: 1343: 1055: 1015: 903: 876: 732: 510: 415: 369: 337: 336:{\displaystyle \pi /6} 309: 308:{\displaystyle \pi /6} 253:Spherical trigonometry 5235: 5106:Now we can eliminate 5097: 5032: 4951:or, noting cos 2 4942: 4836: 4711:(best done privately) 4667: 4587: 4472: 4430: 4386: 4208: 4075: 3967: 3905:, a better formula is 3897:. So, recalling that 3791: 3585: 3343: 3186: 3029: 2922: 2837: 2788: 2731: 2668: 2551:Calculation completed 2347: 2267: 2149: 1997: 1926: 1843: 1710: 1604: 1543: 1344: 1056: 1016: 902: 875: 733: 511: 416: 370: 338: 310: 5140: 5051: 4965: 4871: 4736: 4618: 4525: 4447: 4402: 4286: 4089: 3977: 3919: 3595: 3389: 3196: 3039: 2937: 2847: 2809: 2760: 2683: 2568: 2538:Coordinate Transform 2298: 2205: 2024: 1941: 1858: 1733: 1619: 1558: 1475: 1234: 1029: 921: 633: 425: 379: 347: 319: 291: 4688: = 0 produces 4239:Pythagorean theorem 3901: = 10 cm/ 3834:Here is the graph: 2368: = 0 produces 465: 5230: 5092: 5027: 4955: = 2cos 4937: 4831: 4662: 4582: 4467: 4425: 4381: 4203: 4070: 3962: 3786: 3580: 3338: 3181: 3024: 2917: 2832: 2783: 2726: 2663: 2342: 2262: 2144: 1992: 1921: 1838: 1705: 1599: 1551:from which I have 1538: 1339: 1051: 1011: 904: 877: 728: 605:Arbitrary username 506: 431: 411: 365: 333: 305: 213:spherical geometry 18:User:NorwegianBlue 5130: = cos 5122: = cos 5041:We also have, as 4819: 4767: 4716:haversine formula 4692: = π/2. 4657: 4577: 4465: 4458: 4374: 4348: 4309: 4216: 4215: 4166: 4148: 4036: 3756: 3702: 3701: 3550: 3496: 3495: 2656: 2630: 2591: 2372: = π/2. 2337: 2257: 2123: 2110: 2062: 1988: 1823: 1534: 1502: 1433: 1405: 1332: 1315: 1314: 1037: 1006: 977: 948: 907:Girard's theorem, 720: 701: 659: 484: 454: 355: 255:may help as will 235: 190:Square (geometry) 122:Theorema egregium 5257: 5239: 5237: 5236: 5231: 5218: 5217: 5196: 5195: 5174: 5173: 5155: 5154: 5101: 5099: 5098: 5093: 5036: 5034: 5033: 5028: 5015: 5014: 4998: 4997: 4946: 4944: 4943: 4938: 4925: 4924: 4840: 4838: 4837: 4832: 4817: 4816: 4783: 4782: 4765: 4764: 4671: 4669: 4668: 4663: 4658: 4650: 4645: 4644: 4591: 4589: 4588: 4583: 4578: 4576: 4559: 4548: 4537: 4536: 4506: 4503: 4501: 4495: 4476: 4474: 4473: 4468: 4466: 4461: 4459: 4451: 4440: 4434: 4432: 4431: 4426: 4390: 4388: 4387: 4382: 4375: 4349: 4326: 4321: 4310: 4302: 4212: 4210: 4209: 4204: 4197: 4196: 4184: 4180: 4167: 4165: 4157: 4156: 4146: 4141: 4136: 4135: 4117: 4116: 4093: 4079: 4077: 4076: 4071: 4067: 4066: 4054: 4050: 4037: 4029: 4024: 4023: 4005: 4004: 3981: 3971: 3969: 3968: 3963: 3959: 3958: 3957: 3936: 3913: 3912: 3841: 3801:the formulae of 3795: 3793: 3792: 3787: 3784: 3783: 3771: 3767: 3757: 3749: 3744: 3743: 3725: 3724: 3709: 3705: 3703: 3700: 3683: 3672: 3671: 3661: 3660: 3631: 3630: 3589: 3587: 3586: 3581: 3578: 3577: 3565: 3561: 3551: 3543: 3538: 3537: 3519: 3518: 3503: 3499: 3497: 3494: 3477: 3466: 3465: 3455: 3454: 3431: 3430: 3362: 3347: 3345: 3344: 3339: 3336: 3335: 3323: 3319: 3303: 3302: 3284: 3283: 3262: 3261: 3232: 3231: 3190: 3188: 3187: 3182: 3179: 3178: 3166: 3162: 3146: 3145: 3127: 3126: 3105: 3104: 3081: 3080: 3033: 3031: 3030: 3025: 3022: 3021: 2979: 2978: 2926: 2924: 2923: 2918: 2905: 2904: 2877: 2876: 2841: 2839: 2838: 2833: 2792: 2790: 2789: 2784: 2735: 2733: 2732: 2727: 2713: 2712: 2672: 2670: 2669: 2664: 2657: 2631: 2608: 2603: 2592: 2584: 2351: 2349: 2348: 2343: 2338: 2330: 2325: 2324: 2271: 2269: 2268: 2263: 2258: 2256: 2239: 2228: 2217: 2216: 2153: 2151: 2150: 2145: 2138: 2134: 2124: 2122: 2121: 2116: 2112: 2111: 2088: 2065: 2063: 2055: 2045: 2044: 2001: 1999: 1998: 1993: 1989: 1966: 1930: 1928: 1927: 1922: 1870: 1869: 1847: 1845: 1844: 1839: 1835: 1831: 1824: 1822: 1815: 1814: 1801: 1794: 1793: 1783: 1770: 1769: 1757: 1756: 1714: 1712: 1711: 1706: 1684: 1683: 1662: 1661: 1643: 1642: 1608: 1606: 1605: 1600: 1547: 1545: 1544: 1539: 1535: 1533: 1519: 1508: 1503: 1501: 1490: 1479: 1432: 1404: 1348: 1346: 1345: 1340: 1338: 1334: 1333: 1325: 1320: 1316: 1307: 1306: 1291: 1290: 1279: 1270: 1269: 1249: 1248: 1060: 1058: 1057: 1052: 1038: 1033: 1020: 1018: 1017: 1012: 1007: 1005: 994: 983: 978: 976: 965: 954: 949: 947: 936: 925: 838:I have posted a 771: 737: 735: 734: 729: 721: 713: 702: 694: 689: 688: 670: 669: 660: 652: 515: 513: 512: 507: 496: 485: 483: 482: 467: 464: 460: 455: 450: 447: 443: 420: 418: 417: 412: 404: 403: 391: 390: 374: 372: 371: 366: 361: 356: 351: 342: 340: 339: 334: 329: 314: 312: 311: 306: 301: 282: 233: 84: 5265: 5264: 5260: 5259: 5258: 5256: 5255: 5254: 5247: 5209: 5187: 5165: 5146: 5138: 5137: 5049: 5048: 5006: 4989: 4963: 4962: 4916: 4869: 4868: 4860: 4857: = ⁄ 4852: 4849: = ⁄ 4774: 4734: 4733: 4705: 4636: 4616: 4615: 4560: 4549: 4528: 4523: 4522: 4512: 4505: 4502: 4500: 4497: 4494: 4491: 4445: 4444: 4400: 4399: 4284: 4283: 4274: 4269: 4188: 4158: 4142: 4127: 4105: 4101: 4097: 4087: 4086: 4058: 4015: 3993: 3989: 3985: 3975: 3974: 3922: 3917: 3916: 3775: 3735: 3713: 3684: 3673: 3669: 3665: 3649: 3645: 3641: 3607: 3593: 3592: 3569: 3529: 3507: 3478: 3467: 3463: 3459: 3443: 3439: 3435: 3401: 3387: 3386: 3327: 3294: 3272: 3250: 3246: 3242: 3208: 3194: 3193: 3170: 3137: 3115: 3093: 3089: 3085: 3051: 3037: 3036: 3013: 2949: 2935: 2934: 2896: 2868: 2845: 2844: 2807: 2806: 2801: 2758: 2757: 2704: 2681: 2680: 2566: 2565: 2553: 2540: 2429: 2425: 2421: 2417: 2413: 2409: 2405: 2316: 2296: 2295: 2240: 2229: 2208: 2203: 2202: 2077: 2073: 2072: 2053: 2049: 2033: 2022: 2021: 1939: 1938: 1861: 1856: 1855: 1806: 1802: 1785: 1784: 1781: 1777: 1761: 1748: 1731: 1730: 1675: 1653: 1634: 1617: 1616: 1556: 1555: 1520: 1509: 1491: 1480: 1473: 1472: 1446: 1444:new calculation 1298: 1280: 1274: 1258: 1254: 1250: 1240: 1232: 1231: 1027: 1026: 995: 984: 966: 955: 937: 926: 919: 918: 853: 797:on a sphere?)-- 777: 680: 661: 631: 630: 570:199.201.168.100 474: 423: 422: 395: 382: 377: 376: 345: 344: 317: 316: 289: 288: 275: 82: 29: 22: 21: 20: 12: 11: 5: 5263: 5261: 5253: 5252: 5251: 5250: 5249: 5248: 5245: 5242: 5241: 5240: 5227: 5224: 5221: 5216: 5212: 5208: 5205: 5202: 5199: 5194: 5190: 5186: 5183: 5180: 5177: 5172: 5168: 5164: 5161: 5158: 5153: 5149: 5145: 5104: 5103: 5102: 5089: 5086: 5083: 5080: 5077: 5074: 5071: 5068: 5065: 5062: 5059: 5056: 5039: 5038: 5037: 5024: 5021: 5018: 5013: 5009: 5004: 5001: 4996: 4992: 4988: 4985: 4982: 4979: 4976: 4973: 4970: 4949: 4948: 4947: 4934: 4931: 4928: 4923: 4919: 4915: 4912: 4909: 4906: 4903: 4900: 4897: 4894: 4891: 4888: 4885: 4882: 4879: 4876: 4858: 4850: 4843: 4842: 4841: 4828: 4825: 4822: 4815: 4812: 4809: 4806: 4803: 4800: 4797: 4794: 4789: 4786: 4781: 4777: 4773: 4770: 4763: 4760: 4757: 4754: 4751: 4748: 4745: 4742: 4712: 4706: 4698: 4697: 4696: 4695: 4694: 4693: 4674: 4673: 4672: 4661: 4656: 4653: 4648: 4643: 4639: 4635: 4632: 4629: 4626: 4623: 4594: 4593: 4592: 4581: 4575: 4572: 4569: 4566: 4563: 4558: 4555: 4552: 4546: 4543: 4540: 4535: 4531: 4511: 4508: 4498: 4490: 4487: 4464: 4457: 4454: 4422: 4419: 4416: 4413: 4410: 4407: 4392: 4391: 4379: 4373: 4370: 4367: 4364: 4361: 4358: 4355: 4352: 4347: 4344: 4341: 4338: 4335: 4332: 4329: 4324: 4319: 4316: 4313: 4308: 4305: 4300: 4297: 4294: 4291: 4273: 4270: 4268: 4265: 4264: 4263: 4262: 4261: 4229: 4228: 4220: 4219: 4218: 4217: 4214: 4213: 4200: 4195: 4191: 4187: 4183: 4179: 4176: 4173: 4170: 4164: 4161: 4155: 4152: 4145: 4139: 4134: 4130: 4126: 4123: 4120: 4115: 4112: 4108: 4104: 4100: 4096: 4084: 4081: 4080: 4065: 4061: 4057: 4053: 4049: 4046: 4043: 4040: 4035: 4032: 4027: 4022: 4018: 4014: 4011: 4008: 4003: 4000: 3996: 3992: 3988: 3984: 3972: 3956: 3953: 3950: 3947: 3944: 3941: 3935: 3932: 3929: 3926: 3907: 3906: 3797: 3796: 3782: 3778: 3774: 3770: 3766: 3763: 3760: 3755: 3752: 3747: 3742: 3738: 3734: 3731: 3728: 3723: 3720: 3716: 3712: 3708: 3699: 3696: 3693: 3690: 3687: 3682: 3679: 3676: 3668: 3664: 3659: 3656: 3652: 3648: 3644: 3640: 3637: 3634: 3629: 3626: 3623: 3620: 3617: 3614: 3610: 3606: 3603: 3600: 3590: 3576: 3572: 3568: 3564: 3560: 3557: 3554: 3549: 3546: 3541: 3536: 3532: 3528: 3525: 3522: 3517: 3514: 3510: 3506: 3502: 3493: 3490: 3487: 3484: 3481: 3476: 3473: 3470: 3462: 3458: 3453: 3450: 3446: 3442: 3438: 3434: 3429: 3426: 3423: 3420: 3417: 3414: 3411: 3408: 3404: 3400: 3397: 3394: 3349: 3348: 3334: 3330: 3326: 3322: 3318: 3315: 3312: 3309: 3306: 3301: 3297: 3293: 3290: 3287: 3282: 3279: 3275: 3271: 3268: 3265: 3260: 3257: 3253: 3249: 3245: 3241: 3238: 3235: 3230: 3227: 3224: 3221: 3218: 3215: 3211: 3207: 3204: 3201: 3191: 3177: 3173: 3169: 3165: 3161: 3158: 3155: 3152: 3149: 3144: 3140: 3136: 3133: 3130: 3125: 3122: 3118: 3114: 3111: 3108: 3103: 3100: 3096: 3092: 3088: 3084: 3079: 3076: 3073: 3070: 3067: 3064: 3061: 3058: 3054: 3050: 3047: 3044: 3034: 3020: 3016: 3012: 3009: 3006: 3003: 3000: 2997: 2994: 2991: 2988: 2985: 2982: 2977: 2974: 2971: 2968: 2965: 2962: 2959: 2956: 2952: 2948: 2945: 2942: 2928: 2927: 2915: 2911: 2908: 2903: 2899: 2895: 2892: 2889: 2886: 2883: 2880: 2875: 2871: 2867: 2864: 2861: 2858: 2855: 2852: 2842: 2829: 2826: 2823: 2820: 2817: 2814: 2780: 2777: 2774: 2771: 2768: 2765: 2750: 2749: 2748: 2747: 2746: 2745: 2738: 2737: 2736: 2725: 2722: 2719: 2716: 2711: 2707: 2703: 2700: 2697: 2694: 2691: 2688: 2661: 2655: 2652: 2649: 2646: 2643: 2640: 2637: 2634: 2629: 2626: 2623: 2620: 2617: 2614: 2611: 2606: 2601: 2598: 2595: 2590: 2587: 2582: 2579: 2576: 2573: 2552: 2549: 2539: 2536: 2535: 2534: 2533: 2532: 2531: 2530: 2529: 2528: 2527: 2526: 2525: 2524: 2509: 2505: 2482: 2462: 2459:dihedral angle 2442: 2441: 2440: 2439: 2438: 2437: 2436: 2435: 2427: 2423: 2419: 2415: 2411: 2407: 2403: 2393: 2392: 2391: 2390: 2389: 2388: 2373: 2354: 2353: 2352: 2341: 2336: 2333: 2328: 2323: 2319: 2315: 2312: 2309: 2306: 2303: 2280:is 10 cm/ 2274: 2273: 2272: 2261: 2255: 2252: 2249: 2246: 2243: 2238: 2235: 2232: 2226: 2223: 2220: 2215: 2211: 2197: 2186: 2185: 2184: 2155: 2154: 2141: 2137: 2133: 2130: 2127: 2120: 2115: 2109: 2106: 2103: 2100: 2097: 2094: 2091: 2086: 2083: 2080: 2076: 2071: 2068: 2061: 2058: 2052: 2048: 2043: 2040: 2036: 2032: 2029: 2005:and using cos 2003: 2002: 1987: 1984: 1981: 1978: 1975: 1972: 1969: 1964: 1961: 1958: 1955: 1952: 1949: 1946: 1932: 1931: 1918: 1915: 1912: 1909: 1906: 1903: 1900: 1897: 1894: 1891: 1888: 1885: 1882: 1879: 1876: 1873: 1868: 1864: 1849: 1848: 1834: 1830: 1827: 1821: 1818: 1813: 1809: 1805: 1800: 1797: 1792: 1788: 1780: 1776: 1773: 1768: 1764: 1760: 1755: 1751: 1747: 1744: 1741: 1738: 1716: 1715: 1702: 1699: 1696: 1693: 1690: 1687: 1682: 1678: 1674: 1671: 1668: 1665: 1660: 1656: 1652: 1649: 1646: 1641: 1637: 1633: 1630: 1627: 1624: 1610: 1609: 1596: 1593: 1590: 1587: 1584: 1581: 1578: 1575: 1572: 1569: 1566: 1563: 1549: 1548: 1532: 1529: 1526: 1523: 1518: 1515: 1512: 1506: 1500: 1497: 1494: 1489: 1486: 1483: 1445: 1442: 1441: 1440: 1439: 1438: 1437: 1436: 1409: 1408: 1397: 1396: 1395: 1394: 1393: 1392: 1391: 1390: 1389: 1351: 1350: 1349: 1337: 1331: 1328: 1323: 1319: 1313: 1310: 1305: 1301: 1297: 1294: 1289: 1286: 1283: 1277: 1273: 1268: 1265: 1261: 1257: 1253: 1247: 1243: 1239: 1219: 1218: 1217: 1216: 1215: 1214: 1213: 1212: 1211: 1210: 1209: 1208: 1207: 1206: 1160: 1159: 1158: 1157: 1156: 1155: 1119: 1118: 1117: 1116: 1093: 1092: 1076: 1075: 1050: 1047: 1044: 1041: 1036: 1022: 1021: 1010: 1004: 1001: 998: 993: 990: 987: 981: 975: 972: 969: 964: 961: 958: 952: 946: 943: 940: 935: 932: 929: 916: 914: 892: 891: 881: 880: 865: 864: 863: 862: 852: 849: 848: 847: 835: 834: 833: 832: 831: 830: 829: 828: 808: 807: 806: 805: 765: 764: 756: 755: 745: 738: 727: 724: 719: 716: 711: 708: 705: 700: 697: 692: 687: 683: 679: 676: 673: 668: 664: 658: 655: 650: 647: 644: 641: 638: 627: 626: 621: 620: 611: 610: 609: 608: 574: 573: 522: 521: 518:Cthulhu.mythos 505: 502: 499: 495: 491: 488: 481: 477: 473: 470: 463: 459: 453: 446: 442: 438: 434: 430: 410: 407: 402: 398: 394: 389: 385: 364: 360: 354: 332: 328: 324: 304: 300: 296: 274: 271: 248: 247: 211:Is this about 209: 208: 200: 199: 198: 197: 183: 182: 174: 161: 160: 151: 150: 142: 141: 132: 131: 130: 129: 112: 111: 110: 109: 108: 107: 106: 105: 95: 94: 93: 92: 91: 90: 70: 69: 68: 67: 62:curvature. --- 49: 48: 28: 25: 23: 15: 14: 13: 10: 9: 6: 4: 3: 2: 5262: 5246: 5243: 5225: 5222: 5214: 5210: 5203: 5200: 5192: 5188: 5184: 5181: 5175: 5170: 5166: 5159: 5156: 5151: 5147: 5136: 5135: 5133: 5129: 5125: 5121: 5117: 5114:and sin 5113: 5109: 5105: 5087: 5084: 5081: 5078: 5075: 5072: 5069: 5066: 5063: 5060: 5057: 5054: 5047: 5046: 5044: 5040: 5022: 5019: 5016: 5011: 5007: 5002: 4999: 4994: 4990: 4986: 4983: 4980: 4977: 4974: 4971: 4968: 4961: 4960: 4958: 4954: 4950: 4932: 4929: 4926: 4921: 4917: 4910: 4907: 4904: 4901: 4898: 4895: 4889: 4886: 4883: 4880: 4877: 4874: 4867: 4866: 4864: 4856: 4848: 4844: 4826: 4823: 4820: 4787: 4784: 4779: 4775: 4771: 4768: 4732: 4731: 4729: 4725: 4721: 4717: 4713: 4710: 4707: 4704: 4703: 4702: 4701: 4700: 4699: 4691: 4687: 4683: 4679: 4675: 4659: 4654: 4651: 4646: 4641: 4637: 4633: 4630: 4627: 4624: 4621: 4614: 4613: 4611: 4607: 4603: 4599: 4595: 4579: 4573: 4570: 4567: 4564: 4561: 4556: 4553: 4550: 4544: 4541: 4538: 4533: 4529: 4521: 4520: 4518: 4517: 4516: 4515: 4514: 4513: 4509: 4507: 4496: 4488: 4486: 4484: 4480: 4462: 4455: 4452: 4441: 4439: 4417: 4411: 4408: 4405: 4397: 4377: 4371: 4368: 4365: 4362: 4359: 4356: 4353: 4350: 4345: 4342: 4339: 4336: 4333: 4330: 4327: 4322: 4317: 4314: 4311: 4306: 4303: 4298: 4295: 4292: 4289: 4282: 4281: 4280: 4278: 4271: 4266: 4259: 4258:NorwegianBlue 4255: 4251: 4247: 4246: 4244: 4240: 4235: 4231: 4230: 4226: 4222: 4221: 4198: 4193: 4189: 4185: 4181: 4177: 4174: 4171: 4162: 4159: 4143: 4137: 4132: 4128: 4124: 4118: 4113: 4110: 4106: 4102: 4098: 4094: 4085: 4083: 4082: 4063: 4059: 4055: 4051: 4047: 4044: 4041: 4033: 4030: 4025: 4020: 4016: 4012: 4006: 4001: 3998: 3994: 3990: 3986: 3982: 3973: 3915: 3914: 3911: 3910: 3909: 3908: 3904: 3900: 3896: 3892: 3888: 3885:, or simply 2 3884: 3880: 3876: 3872: 3868: 3864: 3860: 3859: 3858: 3856: 3855:NorwegianBlue 3851: 3850: 3849: 3842: 3840: 3835: 3832: 3830: 3826: 3820: 3818: 3814: 3810: 3808: 3804: 3780: 3776: 3772: 3768: 3764: 3761: 3753: 3750: 3745: 3740: 3736: 3732: 3726: 3721: 3718: 3714: 3710: 3706: 3697: 3694: 3691: 3688: 3685: 3680: 3677: 3674: 3666: 3662: 3657: 3654: 3650: 3646: 3642: 3638: 3635: 3632: 3627: 3624: 3621: 3618: 3615: 3612: 3608: 3604: 3601: 3598: 3591: 3574: 3570: 3566: 3562: 3558: 3555: 3547: 3544: 3539: 3534: 3530: 3526: 3520: 3515: 3512: 3508: 3504: 3500: 3491: 3488: 3485: 3482: 3479: 3474: 3471: 3468: 3460: 3456: 3451: 3448: 3444: 3440: 3436: 3432: 3427: 3424: 3421: 3418: 3415: 3412: 3409: 3406: 3402: 3398: 3395: 3392: 3385: 3384: 3383: 3381: 3380: 3374: 3373: 3368: 3363: 3361: 3356: 3354: 3332: 3328: 3324: 3320: 3316: 3313: 3307: 3304: 3299: 3295: 3291: 3285: 3280: 3277: 3273: 3269: 3266: 3263: 3258: 3255: 3251: 3247: 3243: 3239: 3236: 3233: 3228: 3225: 3222: 3219: 3216: 3213: 3209: 3205: 3202: 3199: 3192: 3175: 3171: 3167: 3163: 3159: 3156: 3150: 3147: 3142: 3138: 3134: 3128: 3123: 3120: 3116: 3112: 3109: 3106: 3101: 3098: 3094: 3090: 3086: 3082: 3077: 3074: 3071: 3068: 3065: 3062: 3059: 3056: 3052: 3048: 3045: 3042: 3035: 3018: 3014: 3010: 3004: 3001: 2998: 2995: 2992: 2989: 2986: 2980: 2975: 2972: 2969: 2966: 2963: 2960: 2957: 2954: 2950: 2946: 2943: 2940: 2933: 2932: 2931: 2913: 2909: 2906: 2901: 2897: 2893: 2890: 2887: 2884: 2881: 2878: 2873: 2869: 2865: 2862: 2859: 2856: 2853: 2850: 2843: 2827: 2824: 2821: 2818: 2815: 2812: 2805: 2804: 2803: 2799: 2798: 2797: 2775: 2769: 2766: 2763: 2755: 2743: 2739: 2723: 2720: 2717: 2714: 2709: 2705: 2701: 2698: 2695: 2692: 2689: 2686: 2679: 2678: 2676: 2675: 2674: 2673: 2659: 2653: 2650: 2647: 2644: 2641: 2638: 2635: 2632: 2627: 2624: 2621: 2618: 2615: 2612: 2609: 2604: 2599: 2596: 2593: 2588: 2585: 2580: 2577: 2574: 2571: 2564: 2563: 2562: 2560: 2559: 2550: 2548: 2546: 2537: 2522: 2521:NorwegianBlue 2518: 2517: 2515: 2510: 2506: 2503: 2499: 2495: 2490: 2488: 2483: 2480: 2476: 2472: 2468: 2463: 2460: 2456: 2452: 2451: 2450: 2449: 2448: 2447: 2446: 2445: 2444: 2443: 2433: 2432:NorwegianBlue 2401: 2400: 2399: 2398: 2397: 2396: 2395: 2394: 2386: 2382: 2378: 2374: 2371: 2367: 2363: 2359: 2355: 2339: 2334: 2331: 2326: 2321: 2317: 2313: 2310: 2307: 2304: 2301: 2294: 2293: 2291: 2287: 2283: 2279: 2275: 2259: 2253: 2250: 2247: 2244: 2241: 2236: 2233: 2230: 2224: 2221: 2218: 2213: 2209: 2201: 2200: 2198: 2194: 2193: 2191: 2190:NorwegianBlue 2187: 2183: 2179: 2178: 2176: 2175: 2173: 2168: 2167: 2166: 2164: 2160: 2139: 2135: 2131: 2128: 2125: 2118: 2113: 2107: 2104: 2101: 2098: 2095: 2092: 2089: 2084: 2081: 2078: 2074: 2069: 2066: 2059: 2056: 2050: 2046: 2041: 2038: 2034: 2030: 2027: 2020: 2019: 2018: 2016: 2012: 2008: 1985: 1982: 1979: 1976: 1973: 1970: 1967: 1962: 1959: 1956: 1953: 1950: 1947: 1944: 1937: 1936: 1935: 1916: 1913: 1910: 1907: 1904: 1901: 1898: 1895: 1892: 1889: 1886: 1883: 1880: 1877: 1874: 1871: 1866: 1862: 1854: 1853: 1852: 1832: 1828: 1825: 1819: 1816: 1811: 1807: 1803: 1798: 1795: 1790: 1786: 1778: 1774: 1771: 1766: 1762: 1758: 1753: 1749: 1745: 1742: 1739: 1736: 1729: 1728: 1727: 1725: 1721: 1700: 1694: 1691: 1688: 1685: 1680: 1676: 1672: 1666: 1663: 1658: 1654: 1650: 1647: 1644: 1639: 1635: 1631: 1628: 1625: 1622: 1615: 1614: 1613: 1594: 1591: 1588: 1585: 1582: 1579: 1576: 1573: 1570: 1567: 1564: 1561: 1554: 1553: 1552: 1530: 1527: 1524: 1521: 1516: 1513: 1510: 1504: 1498: 1495: 1492: 1487: 1484: 1481: 1471: 1470: 1469: 1467: 1463: 1459: 1455: 1451: 1443: 1434: 1430: 1426: 1421: 1420: 1418: 1417:NorwegianBlue 1413: 1412: 1411: 1410: 1406: 1402: 1398: 1387: 1383: 1379: 1375: 1371: 1367: 1363: 1359: 1358: 1356: 1352: 1335: 1329: 1326: 1321: 1317: 1311: 1308: 1303: 1299: 1295: 1292: 1287: 1284: 1281: 1275: 1271: 1266: 1263: 1259: 1255: 1251: 1245: 1241: 1237: 1230: 1229: 1227: 1226: 1225: 1224: 1223: 1222: 1221: 1220: 1204: 1200: 1196: 1192: 1191: 1189: 1185: 1184: 1182: 1181:NorwegianBlue 1178: 1174: 1170: 1169: 1168: 1167: 1166: 1165: 1164: 1163: 1162: 1161: 1153: 1149: 1145: 1141: 1137: 1133: 1129: 1125: 1124: 1123: 1122: 1121: 1120: 1114: 1110: 1106: 1102: 1101: 1099: 1095: 1094: 1090: 1086: 1082: 1078: 1077: 1073: 1068: 1067: 1066: 1064: 1063:NorwegianBlue 1048: 1045: 1042: 1039: 1034: 1008: 1002: 999: 996: 991: 988: 985: 979: 973: 970: 967: 962: 959: 956: 950: 944: 941: 938: 933: 930: 927: 917: 915: 912: 908: 901: 897: 896: 895: 889: 888: 887: 885: 874: 870: 869: 868: 860: 859: 858: 857: 856: 850: 845: 844:NorwegianBlue 841: 837: 836: 826: 825:NorwegianBlue 822: 821: 819: 814: 813: 812: 811: 810: 809: 803: 800: 796: 792: 788: 787: 786: 785: 784: 782: 781:NorwegianBlue 775: 774:great circles 770: 762: 758: 757: 753: 750: 746: 743: 739: 717: 714: 709: 706: 703: 698: 695: 685: 681: 677: 671: 666: 656: 653: 648: 645: 642: 639: 629: 628: 623: 622: 618: 617:NorwegianBlue 613: 612: 606: 601: 600: 599: 598: 597: 595: 591: 587: 583: 579: 571: 567: 566: 565: 563: 559: 555: 551: 547: 543: 539: 535: 531: 527: 519: 503: 500: 497: 493: 489: 486: 479: 475: 471: 468: 461: 457: 451: 444: 440: 436: 432: 428: 408: 405: 400: 396: 392: 387: 383: 362: 358: 352: 330: 326: 322: 302: 298: 294: 285: 284: 283: 281: 272: 270: 267: 265: 262: 258: 254: 245: 241: 240: 239: 237: 236: 229: 225: 220: 218: 214: 206: 202: 201: 195: 191: 188:According to 187: 186: 185: 184: 180: 175: 172: 171: 170: 167: 164: 158: 153: 152: 148: 144: 143: 139: 134: 133: 127: 123: 119: 118: 117: 116: 115: 103: 102: 101: 100: 99: 98: 97: 96: 88: 85: 80: 76: 75: 74: 73: 72: 71: 65: 61: 57: 53: 52: 51: 50: 46: 42: 38: 34: 33: 32: 26: 19: 5131: 5127: 5123: 5119: 5115: 5111: 5107: 4956: 4952: 4862: 4861:(1-cos 4854: 4853:versin 4846: 4727: 4723: 4719: 4709:Calculations 4708: 4689: 4685: 4681: 4677: 4612:, for which 4609: 4605: 4601: 4597: 4504: 4492: 4489:Computations 4482: 4478: 4442: 4395: 4393: 4275: 4249: 4233: 4224: 3902: 3898: 3894: 3886: 3882: 3878: 3874: 3870: 3866: 3862: 3852: 3846: 3843: 3836: 3833: 3821: 3800: 3798: 3377: 3375: 3371: 3364: 3357: 3352: 3350: 2929: 2800: 2794: 2753: 2751: 2556: 2554: 2541: 2501: 2497: 2493: 2486: 2478: 2474: 2470: 2466: 2455:great circle 2380: 2376: 2369: 2365: 2361: 2357: 2292:, for which 2289: 2285: 2281: 2277: 2180: 2158: 2156: 2014: 2010: 2006: 2004: 1933: 1850: 1723: 1719: 1717: 1611: 1550: 1465: 1461: 1457: 1453: 1449: 1447: 1381: 1377: 1373: 1369: 1365: 1361: 1198: 1194: 1176: 1147: 1143: 1139: 1135: 1134:/ v(1 – cos 1131: 1127: 1108: 1104: 1080: 1023: 893: 883: 882: 866: 854: 766: 760: 589: 585: 581: 577: 575: 557: 553: 549: 545: 541: 537: 533: 529: 525: 523: 276: 268: 249: 231: 223: 221: 210: 168: 165: 162: 113: 59: 55: 39:is 2D and a 30: 3869:is half of 3382:works out: 2489:on a sphere 1456:and angles 795:solid angle 257:solid angle 5045:observed, 3891:User:lethe 3848:user page. 2796:user page. 1934:So I have 1425:Salix alba 1085:Salix alba 791:WP:RD/Math 79:M1ss1ontom 5182:− 5157:− 5082:⁡ 5073:⁡ 5058:⁡ 5017:⁡ 5000:⁡ 4984:− 4972:⁡ 4927:⁡ 4905:⁡ 4899:− 4884:⁡ 4878:− 4785:⁡ 4726: = 2 4647:⁡ 4634:− 4625:⁡ 4608: = 2 4571:⁡ 4554:⁡ 4539:⁡ 4369:− 4360:⁡ 4351:− 4340:⁡ 4315:⁡ 4293:⁡ 4186:× 4178:π 4172:− 4138:⁡ 4125:− 4119:⁡ 4111:− 4056:× 4048:π 4042:− 4026:⁡ 4013:− 4007:⁡ 3999:− 3773:× 3765:π 3762:− 3746:⁡ 3733:− 3727:⁡ 3719:− 3695:⁡ 3678:⁡ 3663:⁡ 3655:− 3639:× 3567:× 3559:π 3556:− 3540:⁡ 3527:− 3521:⁡ 3513:− 3489:⁡ 3472:⁡ 3457:⁡ 3449:− 3325:× 3317:π 3314:− 3305:− 3286:⁡ 3278:− 3264:⁡ 3256:− 3240:× 3168:× 3160:π 3157:− 3148:− 3129:⁡ 3121:− 3107:⁡ 3099:− 3011:× 3005:π 3002:− 2907:− 2885:− 2879:⁡ 2854:⁡ 2816:⁡ 2721:− 2715:⁡ 2690:⁡ 2651:− 2642:⁡ 2633:− 2622:⁡ 2597:⁡ 2575:⁡ 2379:-2π) 2327:⁡ 2314:− 2305:⁡ 2288: = 2 2251:⁡ 2234:⁡ 2219:⁡ 2129:⁡ 2102:⁡ 2079:− 2070:− 2047:⁡ 2039:− 1980:⁡ 1963:± 1957:− 1948:⁡ 1908:⁡ 1893:− 1887:⁡ 1872:⁡ 1826:− 1817:⁡ 1796:⁡ 1772:⁡ 1740:⁡ 1692:− 1686:⁡ 1664:⁡ 1645:⁡ 1626:⁡ 1589:⁡ 1580:⁡ 1565:⁡ 1525:⁡ 1514:⁡ 1496:⁡ 1485:⁡ 1327:π 1322:− 1309:⁡ 1296:− 1285:⁡ 1272:⁡ 1264:− 1072:Dysprosia 1040:× 1000:⁡ 989:⁡ 971:⁡ 960:⁡ 942:⁡ 931:⁡ 840:follow-up 742:mathworld 715:π 710:⁡ 704:− 696:π 654:π 649:⁡ 487:− 472:− 433:∫ 323:π 295:π 2487:triangle 905:I found 799:jpgordon 749:jpgordon 269:adoroph 244:SGBailey 228:Grutness 194:SGBailey 147:SGBailey 138:SGBailey 56:positive 3845:on my 3829:KSmrq's 1460:, and 2 1429:Lambiam 1401:Lambiam 1081:squares 818:HappyVR 264:HappyVR 4818: 4766: 4596:where 4234:always 4147: 3817:(nans) 2453:Every 2276:where 2013:/2sin 2009:= sin 1130:= sin 1107:= cos 217:Yanwen 179:Stefan 45:Stefan 41:sphere 37:square 5043:lethe 4277:lethe 4243:KSmrq 3825:KSmrq 3813:KSmrq 3807:KSmrq 3803:lethe 3379:KSmrq 3367:KSmrq 2742:lethe 2558:lethe 2545:Nimur 2514:KSmrq 2426:and P 2418:and P 2385:KSmrq 2172:KSmrq 2163:lethe 1386:lethe 1355:lethe 1203:lethe 1188:lethe 1173:lethe 1152:lethe 1113:lethe 1098:lethe 205:Swift 157:Swift 124:. --- 87:rs2k4 16:< 5126:and 4959:-1, 4718:for 3805:and 2383:. -- 1380:/360 1146:and 1138:). 1111:. - 1089:talk 588:and 552:and 544:and 536:and 234:wha? 120:See 60:zero 5079:sin 5070:cos 5055:sin 5008:sin 4991:sin 4969:cos 4918:sin 4902:cos 4881:cos 4865:), 4776:sin 4638:tan 4622:cos 4568:cos 4551:cos 4530:cos 4477:as 4357:cos 4337:cos 4312:csc 4290:cos 4254:NaN 4129:tan 4107:cos 4017:tan 3995:cos 3737:tan 3715:cos 3692:cos 3675:cos 3651:cos 3531:tan 3509:cos 3486:cos 3469:cos 3445:cos 3274:cos 3252:cos 3117:cos 3095:cos 2870:cos 2851:cos 2813:cos 2706:cos 2687:cos 2639:cos 2619:cos 2594:csc 2572:cos 2494:any 2318:tan 2302:cos 2248:cos 2231:cos 2210:cos 2161:. - 2126:csc 2099:cos 2035:cos 1977:cos 1945:cos 1905:cos 1884:cos 1863:cos 1808:sin 1787:sin 1763:sin 1750:cos 1737:cos 1677:cos 1655:sin 1636:cos 1623:cos 1586:sin 1577:cos 1562:sin 1522:sin 1511:sin 1493:sin 1482:sin 1384:. - 1300:cos 1282:sin 1260:sin 1197:= 2 1171:To 997:sin 986:sin 968:sin 957:sin 939:sin 928:sin 707:sin 646:sin 594:Gdr 562:Gdr 230:... 5226:0. 5134:, 4730:, 4144:10 3819:. 2512:-- 1726:: 1464:= 1376:+ 1372:/6 1368:+ 1142:= 1043:10 779:-- 657:12 592:. 584:, 560:. 343:)= 155:-- 126:CH 64:CH 5223:= 5220:) 5215:2 5211:y 5207:( 5204:+ 5201:x 5198:) 5193:2 5189:y 5185:2 5179:( 5176:+ 5171:2 5167:x 5163:) 5160:1 5152:2 5148:y 5144:( 5132:a 5128:y 5124:A 5120:x 5116:a 5112:A 5108:c 5088:. 5085:a 5076:A 5067:2 5064:= 5061:c 5023:. 5020:a 5012:2 5003:A 4995:2 4987:2 4981:1 4978:= 4975:c 4957:A 4953:A 4933:, 4930:a 4922:2 4914:) 4911:A 4908:2 4896:1 4893:( 4890:= 4887:c 4875:1 4863:z 4859:2 4855:z 4851:2 4847:z 4827:, 4824:A 4821:2 4814:n 4811:i 4808:s 4805:r 4802:e 4799:v 4796:a 4793:h 4788:a 4780:2 4772:= 4769:c 4762:n 4759:i 4756:s 4753:r 4750:e 4747:v 4744:a 4741:h 4728:A 4724:C 4720:C 4690:C 4686:a 4682:C 4678:a 4660:. 4655:2 4652:a 4642:2 4631:= 4628:C 4610:A 4606:C 4602:R 4598:a 4580:, 4574:a 4565:+ 4562:1 4557:a 4545:= 4542:A 4534:2 4483:a 4479:a 4463:2 4456:2 4453:1 4421:) 4418:a 4415:( 4412:g 4409:= 4406:G 4396:a 4378:. 4372:2 4366:a 4363:2 4354:2 4346:a 4343:2 4334:2 4331:+ 4328:2 4323:2 4318:a 4307:2 4304:1 4299:= 4296:A 4250:C 4225:A 4199:. 4194:2 4190:R 4182:) 4175:2 4169:) 4163:R 4160:2 4154:m 4151:c 4133:2 4122:( 4114:1 4103:4 4099:( 4095:= 4064:2 4060:R 4052:) 4045:2 4039:) 4034:2 4031:a 4021:2 4010:( 4002:1 3991:4 3987:( 3983:= 3955:e 3952:r 3949:a 3946:u 3943:q 3940:s 3934:a 3931:e 3928:r 3925:a 3903:R 3899:a 3895:A 3887:C 3883:C 3881:+ 3879:A 3877:+ 3875:A 3871:C 3867:A 3863:C 3781:2 3777:R 3769:) 3759:) 3754:2 3751:a 3741:2 3730:( 3722:1 3711:+ 3707:) 3698:a 3689:+ 3686:1 3681:a 3667:( 3658:1 3647:2 3643:( 3636:2 3633:= 3628:e 3625:r 3622:a 3619:u 3616:q 3613:s 3609:a 3605:e 3602:r 3599:a 3575:2 3571:R 3563:) 3553:) 3548:2 3545:a 3535:2 3524:( 3516:1 3505:+ 3501:) 3492:a 3483:+ 3480:1 3475:a 3461:( 3452:1 3441:2 3437:( 3433:= 3428:e 3425:l 3422:g 3419:n 3416:a 3413:i 3410:r 3407:t 3403:a 3399:e 3396:r 3393:a 3353:a 3333:2 3329:R 3321:) 3311:) 3308:1 3300:2 3296:G 3292:2 3289:( 3281:1 3270:+ 3267:G 3259:1 3248:2 3244:( 3237:2 3234:= 3229:e 3226:r 3223:a 3220:u 3217:q 3214:s 3210:a 3206:e 3203:r 3200:a 3176:2 3172:R 3164:) 3154:) 3151:1 3143:2 3139:G 3135:2 3132:( 3124:1 3113:+ 3110:G 3102:1 3091:2 3087:( 3083:= 3078:e 3075:l 3072:g 3069:n 3066:a 3063:i 3060:r 3057:t 3053:a 3049:e 3046:r 3043:a 3019:2 3015:R 3008:) 2999:C 2996:+ 2993:B 2990:+ 2987:A 2984:( 2981:= 2976:e 2973:l 2970:g 2967:n 2964:a 2961:i 2958:r 2955:t 2951:a 2947:e 2944:r 2941:a 2914:. 2910:1 2902:2 2898:G 2894:2 2891:= 2888:1 2882:A 2874:2 2866:2 2863:= 2860:A 2857:2 2828:. 2825:G 2822:= 2819:A 2779:) 2776:a 2773:( 2770:g 2767:= 2764:G 2754:a 2724:1 2718:a 2710:2 2702:2 2699:= 2696:a 2693:2 2660:. 2654:2 2648:a 2645:2 2636:2 2628:a 2625:2 2616:2 2613:+ 2610:2 2605:2 2600:a 2589:2 2586:1 2581:= 2578:A 2504:. 2502:R 2498:R 2479:R 2475:R 2471:a 2467:a 2428:2 2424:1 2420:2 2416:1 2412:3 2408:2 2404:1 2381:R 2377:C 2370:C 2366:a 2362:C 2358:a 2340:. 2335:2 2332:a 2322:2 2311:= 2308:C 2290:A 2286:C 2282:R 2278:a 2260:, 2254:a 2245:+ 2242:1 2237:a 2225:= 2222:A 2214:2 2159:s 2140:. 2136:) 2132:a 2119:2 2114:) 2108:a 2105:2 2096:2 2093:+ 2090:2 2085:+ 2082:1 2075:( 2067:1 2060:2 2057:1 2051:( 2042:1 2031:= 2028:A 2015:a 2011:c 2007:A 1986:a 1983:2 1974:2 1971:+ 1968:2 1960:1 1954:= 1951:c 1917:. 1914:a 1911:2 1902:2 1899:= 1896:1 1890:c 1881:2 1878:+ 1875:c 1867:2 1833:) 1829:1 1820:a 1812:2 1804:2 1799:c 1791:2 1779:( 1775:a 1767:2 1759:+ 1754:2 1746:= 1743:c 1724:A 1720:c 1701:. 1698:) 1695:1 1689:A 1681:2 1673:2 1670:( 1667:a 1659:2 1651:+ 1648:a 1640:2 1632:= 1629:c 1595:. 1592:a 1583:A 1574:2 1571:= 1568:c 1531:A 1528:2 1517:c 1505:= 1499:A 1488:a 1466:C 1462:A 1458:A 1454:a 1450:C 1382:R 1378:s 1374:R 1370:s 1366:s 1362:s 1336:) 1330:2 1318:) 1312:a 1304:4 1293:1 1288:a 1276:( 1267:1 1256:2 1252:( 1246:2 1242:R 1238:2 1199:A 1195:C 1177:C 1148:C 1144:B 1140:A 1136:a 1132:a 1128:A 1109:a 1105:c 1087:( 1049:m 1046:c 1035:2 1009:. 1003:C 992:c 980:= 974:B 963:b 951:= 945:A 934:a 890:- 776:. 744:. 726:) 723:) 718:6 699:6 691:( 686:2 682:R 678:2 675:( 672:+ 667:2 663:) 643:R 640:2 637:( 590:c 586:b 582:a 578:c 558:a 554:b 550:a 546:b 542:a 538:b 534:a 530:b 526:a 504:x 501:d 498:2 494:/ 490:1 480:2 476:x 469:1 462:2 458:/ 452:3 445:2 441:/ 437:1 429:4 409:1 406:= 401:2 397:y 393:+ 388:2 384:x 363:2 359:/ 353:3 331:6 327:/ 303:6 299:/ 215:? 83:a

Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.

Index