80:
117:
2971:
2071:
4563:
2770:
572:
5235:
3108:
1918:
1792:
1569:
2427:
3213:
2762:
3835:
4367:
1407:
2450:. In a separable metric space, any pairwise disjoint collection of balls must be countable. In a non-separable space, the same argument shows a pairwise disjoint subfamily exists, but that family need not be countable.
2155:
3961:
in a specific way. The main differences between the
Besicovitch covering theorem and the Vitali covering lemma are that on one hand, the disjointness requirement of Vitali is relaxed to the fact that the number
3547:
4245:
4180:
799:
2620:, each of which has a measure we can more easily compute, or has a special property one would like to exploit. Hence, if we compute the measure of this union, we will have an upper bound on the measure of
440:
5336:
4435:
431:
5662:
1297:
5083:
4111:
3762:
2966:{\displaystyle \lambda _{d}(E)\leq \lambda _{d}{\biggl (}\bigcup _{j\in J}B_{j}{\biggr )}\leq \lambda _{d}{\biggl (}\bigcup _{j\in J'}5B_{j}{\biggr )}\leq \sum _{j\in J'}\lambda _{d}(5B_{j}).}
2676:
1478:
4767:
915:
1050:
673:
4872:
5098:
4943:
1094:
719:
347:
3637:
2220:
1625:
1597:
1444:
5267:
4808:
2618:
158:
110:
1505:
4064:
3870:
3711:
3604:
3578:
3463:
3414:
3374:
3316:
3272:
992:
948:
1823:
4637:
2562:
2066:{\displaystyle \mathbf {H} _{n+1}=\{B\in \mathbf {F} _{n+1}:\ B\cap C=\emptyset ,\ \ \forall C\in \mathbf {G} _{0}\cup \mathbf {G} _{1}\cup \dots \cup \mathbf {G} _{n}\},}
1500:
1330:
5021:
1654:
839:
5804:
4423:
1209:
1155:
613:
1684:
229:
4973:
3767:
120:
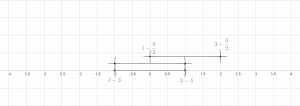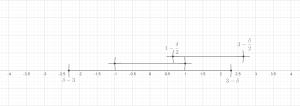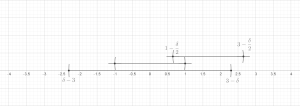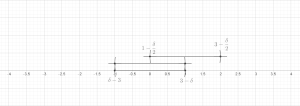
On the top: a collection of balls; the green balls are the disjoint subcollection. On the bottom: the subcollection with three times the radius covers all the balls.
1236:
1121:
199:
290:
1339:
2986:
252:
1175:
2366:
4185:
4116:
2624:. However, it is difficult to compute the measure of the union of all these balls if they overlap. By the Vitali lemma, we may choose a subcollection
4277:
2526:
3119:
2681:
2102:
124:
There are two basic versions of the lemma, a finite version and an infinite version. Both lemmas can be proved in the general setting of a
3487:
5725:
724:
5851:
5777:
5610:
5569:
5594:
5279:
4558:{\displaystyle \sum _{j}\operatorname {diam} (U_{j})^{d}\leq C\sum _{j}\lambda _{d}(U_{j})\leq C\,\lambda _{d}(B)<+\infty }
4580:
The covering lemma can be used as intermediate step in the proof of the following basic form of the Vitali covering theorem.
5357:
The Vitali covering theorem is not valid in infinite-dimensional settings. The first result in this direction was given by
5645:
356:
5403:
3916:
1245:
5033:
4073:
3724:
5640:
1453:
5700:
4717:
5602:
3882:
has finite measure. This is obtained by applying the covering result in the finite measure case, for every integer
855:
2627:
567:{\displaystyle B_{1}\cup B_{2}\cup \dots \cup B_{n}\subseteq 3B_{j_{1}}\cup 3B_{j_{2}}\cup \dots \cup 3B_{j_{m}}.}
3957:
is assigned. Then, as in the Vitali covering lemma, a subcollection of these balls is selected in order to cover
997:
2168:
is a disjoint collection, and is thus countable since the given metric space is separable. Moreover, every ball
618:
5889:
4828:
3659:, the family of balls for the metric associated to the norm is another example. To the contrary, the family of
5230:{\displaystyle \lambda _{d}(Z)\leq \sum _{n>N}\lambda _{d}(5C_{n})=5^{d}\sum _{n>N}\lambda _{d}(C_{n}).}
5894:
5873:
4913:
5899:
1333:
28:
5390:). This result was strengthened in 2003 by Jaroslav Tišer: the Vitali covering theorem in fact fails for
1055:
678:
306:
3609:
2197:
1602:
1574:
1412:
5846:
5243:
4784:
4568:
which excludes the second possibility in the first assertion of the previous theorem. It follows that
2578:
134:
86:
5635:
4045:
3851:
3692:
3585:
3559:
3444:
3395:
3355:
3297:
3253:
2453:
The result may fail if the radii are not bounded: consider the family of all balls centered at 0 in
953:
920:
2529:. As in this proof, the Vitali lemma is frequently used when we are, for instance, considering the
1239:
4620:
2540:
1799:
1483:
1313:
4990:
1630:
804:
350:
202:
1787:{\displaystyle \mathbf {F} _{n}=\{B\in \mathbf {F} :2^{-n-1}R<{\text{rad}}(B)\leq 2^{-n}R\}.}
4395:
1180:
1126:
584:
5773:
5734:
5606:
5565:
4005:
2565:
79:
5394:
infinite-dimensional
Gaussian measure on any (infinite-dimensional) separable Hilbert space.
208:
5860:
5831:
5813:
5791:
5750:
5712:
5681:
5671:
5624:
5583:
5362:
4948:
2534:
5827:
5787:
5746:
5708:
5620:
5579:
3103:{\displaystyle \sum _{j\in J'}\lambda _{d}(5B_{j})=5^{d}\sum _{j\in J'}\lambda _{d}(B_{j})}
2489:
instead of 5. Any constant larger than 3 gives a correct statement of the lemma, but not 3.
1214:
1099:
5864:
5842:
5835:
5823:
5795:
5783:
5754:
5742:
5716:
5704:
5692:
5685:
5628:
5616:
5587:
5575:
5369:
2980:-dimensional ball by a factor of five increases its volume by a factor of 5, we know that
577:
Without loss of generality, we assume that the collection of balls is not empty; that is,
163:
129:
48:
36:
1893:
257:
1564:{\displaystyle \bigcup _{B\in \mathbf {F} }B\subseteq \bigcup _{C\in \mathbf {G} }5\,C.}
234:
5657:
5653:
5557:
3474:
2422:{\displaystyle \bigcup _{B\in \mathbf {F} }B\subseteq \bigcup _{C\in \mathbf {G} }5\,C}
1160:
32:
116:
5883:
5769:
5372:
4572:
is covered, up to a
Lebesgue-negligible set, by the selected disjoint subcollection.
434:
5358:
125:
39:. This lemma is an intermediate step, of independent interest, in the proof of the
5818:
5761:
5341:
Therefore, the term on the right side of the above inequality converges to 0 as
2447:
841:
be such ball with maximal radius (breaking ties arbitrarily), otherwise, we set
20:
3872:
is a collection of intervals that is a Vitali covering for a measurable subset
3830:{\displaystyle \lambda _{d}{\biggl (}E\setminus \bigcup _{j}U_{j}{\biggr )}=0.}
4362:{\displaystyle H^{s}(E)\leq \sum _{j}\mathrm {diam} (U_{j})^{s}+\varepsilon .}
4039:
5738:
16:
Combinatorial and geometric result used in measure theory of
Euclidean spaces
5561:
4070:. Then there exists a (finite or countably infinite) disjoint subcollection
3208:{\displaystyle \lambda _{d}(E)\leq 5^{d}\sum _{j\in J'}\lambda _{d}(B_{j}).}
2757:{\textstyle \bigcup _{j\in J'}5B_{j}\supset \bigcup _{j\in J}B_{j}\supset E}
2443:
1402:{\displaystyle R:=\sup \,\{\mathrm {rad} (B):B\in \mathbf {F} \}<\infty }
2575:, which we know is contained in the union of a certain collection of balls
3721:. Then there exists a finite or countably infinite disjoint subcollection
353:
contained in an arbitrary metric space. Then there exists a subcollection
4008:
instead of
Lebesgue measure. The following theorem applies in that case.
3327:
52:
5676:
4613:
are nondegenerate and have radius less than or equal to 1. By the
4372:
This theorem implies the result of
Lebesgue given above. Indeed, when
3349:
have also been considered, as is shown in the relevant section below.
3345:, but measures other than the Lebesgue measure, and spaces other than
2150:{\displaystyle \mathbf {G} :=\bigcup _{n=0}^{\infty }\mathbf {G} _{n}}
5802:
Tišer, Jaroslav (2003), "Vitali covering theorem in
Hilbert space",
5451:
3542:{\displaystyle \operatorname {diam} (V)^{d}\leq C\,\lambda _{d}(V)}
4240:{\displaystyle \sum _{j}\operatorname {diam} (U_{j})^{s}=\infty .}
115:
78:
44:
5723:
Preiss, David (1979), "Gaussian measures and covering theorems",
128:, typically these results are applied to the special case of the
4175:{\displaystyle H^{s}\left(E\setminus \bigcup _{j}U_{j}\right)=0}
794:{\displaystyle B_{j_{1}}\cup B_{j_{2}}\cup \dots \cup B_{j_{k}}}
5766:
Real analysis. Measure theory, integration, and
Hilbert spaces
4609:
Without loss of generality, one can assume that all balls in
1299:, as needed. This completes the proof of the finite version.
5601:, Cambridge Tracts in Mathematics, vol. 85, Cambridge:
4098:
4051:
3857:
3749:
3698:
3615:
3591:
3565:
3450:
3401:
3361:
3341:
In the classical setting of Vitali, the negligible set is a
3303:
3259:
51:. The theorem states that it is possible to cover, up to a
3999:
3689:
be a measurable set with finite
Lebesgue measure, and let
160:. In both theorems we will use the following notation: if
5847:"Sui gruppi di punti e sulle funzioni di variabili reali"
3992:; on the other hand, the selected balls do cover the set
3423:
5331:{\displaystyle \sum _{n}\lambda _{d}(C_{n})<\infty .}
4878:. But by the Vitali cover property, one can find a ball
4392:-dimensional Lebesgue measure. If a disjoint collection
615:
be the ball of largest radius. Inductively, assume that
4598:
of closed balls, there exists a disjoint subcollection
3416:
that are contained in Ω is also a Vitali covering for
2684:
1802:
858:
260:
166:
5282:
5246:
5101:
5036:
4993:
4951:
4916:
4831:
4787:
4720:
4623:
4438:
4398:
4280:
4262: > 0, we may choose this subcollection {
4188:
4119:
4076:
4048:
3878:
The theorem above remains true without assuming that
3854:
3770:
3727:
3695:
3612:
3588:
3562:
3490:
3447:
3398:
3358:
3300:
3256:
3122:
2989:
2773:
2630:
2581:
2543:
2525:
An application of the Vitali lemma is in proving the
2492:
Using a finer analysis, when the original collection
2369:
2200:
2105:
1921:
1687:
1633:
1605:
1577:
1508:
1486:
1456:
1415:
1342:
1316:
1248:
1217:
1183:
1163:
1129:
1102:
1058:
1000:
956:
923:
807:
727:
681:
621:
587:
443:
359:
309:
237:
211:
137:
89:
3971:
of the selected balls containing an arbitrary point
3582:
The family of cubes is an example of regular family
426:{\displaystyle B_{j_{1}},B_{j_{2}},\dots ,B_{j_{m}}}
5870:
On groups of points and functions of real variables
5663:
4000:
Vitali's covering theorem for the Hausdorff measure
3428:The next covering theorem for the Lebesgue measure
2457:; any disjoint subfamily consists of only one ball
5726:Commentatione Mathematicae Universitatis Carolinae
5330:
5261:
5229:
5077:
5015:
4967:
4937:
4866:
4802:
4761:
4631:
4617:, there exists a countable disjoint subcollection
4557:
4417:
4361:
4239:
4174:
4105:
4058:
4004:One may have a similar objective when considering
3864:
3829:
3756:
3705:
3631:
3598:
3572:
3541:
3457:
3424:Vitali's covering theorem for the Lebesgue measure
3408:
3368:
3310:
3266:
3207:
3102:
2965:
2756:
2670:
2612:
2556:
2421:
2214:
2149:
2065:
1817:
1786:
1648:
1619:
1591:
1563:
1494:
1472:
1438:
1401:
1324:
1292:{\displaystyle B_{i}\subset 3\,B_{j_{k}}\subset X}
1291:
1230:
1203:
1169:
1149:
1115:
1088:
1044:
986:
942:
909:
833:
793:
713:
667:
607:
566:
425:
341:
284:
246:
223:
193:
152:
104:
5805:Transactions of the American Mathematical Society
5078:{\displaystyle Z\subset \bigcup _{n>N}5C_{n}.}
4106:{\displaystyle \{U_{j}\}\subseteq {\mathcal {V}}}
3816:
3783:
3757:{\displaystyle \{U_{j}\}\subseteq {\mathcal {V}}}
3655: ≥ 1. If an arbitrary norm is given on
2902:
2861:
2841:
2808:
1864:, is defined inductively as follows. First, set
4602:which covers E up to a Lebesgue-negligible set.
4425:is regular and contained in a measurable region
2476: > 1, is used instead of 2 for defining
2355:we can conclude by the triangle inequality that
1473:{\displaystyle \mathbf {G} \subset \mathbf {F} }
1349:
5772:: Princeton University Press, pp. xx+402,
5554:Measure Theory and Fine Properties of Functions
5552:Evans, Lawrence C.; Gariepy, Ronald F. (1992),
5454:From the covering lemma to the covering theorem
5378:so that the Vitali covering theorem fails for (
4576:From the covering lemma to the covering theorem
1450:. Then there exists a countable sub-collection
5658:"Sur l'intégration des fonctions discontinues"
4762:{\displaystyle \mathbf {G} _{r}=\{C_{n}\}_{n}}
3223:In the covering theorem, the aim is to cover,
2465:does not contain all the balls in this family.
910:{\textstyle X:=\bigcup _{k=1}^{m}3\,B_{j_{k}}}
5872:" is the paper containing the first proof of
5420:
5418:
4258:-dimensional Hausdorff measure, then for any
3278:is a collection of sets such that, for every
3235:by a disjoint subcollection extracted from a
8:
5510:
5468:
5438:
4750:
4736:
4594:and every Vitali cover of E by a collection
4412:
4399:
4090:
4077:
3844:is a special case of this theorem, in which
3741:
3728:
2671:{\displaystyle \left\{B_{j}:j\in J'\right\}}
2607:
2582:
2468:The constant 5 is not optimal. If the scale
2057:
1943:
1778:
1703:
1390:
1353:
1083:
1065:
1039:
1007:
5852:Atti dell'Accademia delle Scienze di Torino
4769:denote the subcollection of those balls in
4703:, centered at 0. It is enough to show that
4584:
4012:
3915:A somewhat related covering theorem is the
3675:
3643:such that the ratio of sides stays between
2429:immediately follows, completing the proof.
2164:satisfies the requirements of the theorem:
1045:{\displaystyle i\in \{j_{1},\dots ,j_{m}\}}
675:have been chosen. If there is some ball in
3384:is contained in an open set Ω ⊆
668:{\displaystyle B_{j_{1}},\dots ,B_{j_{k}}}
43:. The covering theorem is credited to the
5817:
5675:
5310:
5297:
5287:
5281:
5253:
5248:
5245:
5215:
5202:
5186:
5176:
5160:
5144:
5128:
5106:
5100:
5066:
5047:
5035:
5007:
4992:
4959:
4950:
4930:
4921:
4915:
4867:{\displaystyle K=\bigcup _{n\leq N}C_{n}}
4858:
4842:
4830:
4810:may be finite or countably infinite. Let
4794:
4789:
4786:
4753:
4743:
4727:
4722:
4719:
4624:
4622:
4531:
4526:
4511:
4498:
4488:
4472:
4462:
4443:
4437:
4406:
4397:
4344:
4334:
4313:
4307:
4285:
4279:
4222:
4212:
4193:
4187:
4155:
4145:
4124:
4118:
4097:
4096:
4084:
4075:
4050:
4049:
4047:
3856:
3855:
3853:
3815:
3814:
3808:
3798:
3782:
3781:
3775:
3769:
3748:
3747:
3735:
3726:
3713:be a regular family of closed subsets of
3697:
3696:
3694:
3614:
3613:
3611:
3590:
3589:
3587:
3564:
3563:
3561:
3524:
3519:
3507:
3489:
3449:
3448:
3446:
3400:
3399:
3397:
3360:
3359:
3357:
3302:
3301:
3299:
3258:
3257:
3255:
3193:
3180:
3159:
3149:
3127:
3121:
3091:
3078:
3057:
3047:
3031:
3015:
2994:
2988:
2951:
2935:
2914:
2901:
2900:
2894:
2870:
2860:
2859:
2853:
2840:
2839:
2833:
2817:
2807:
2806:
2800:
2778:
2772:
2742:
2726:
2713:
2689:
2683:
2640:
2629:
2589:
2580:
2548:
2542:
2442:, the initial collection of balls can be
2415:
2405:
2398:
2381:
2374:
2368:
2207:
2199:
2141:
2136:
2129:
2118:
2106:
2104:
2051:
2046:
2030:
2025:
2015:
2010:
1958:
1953:
1928:
1923:
1920:
1809:
1804:
1801:
1766:
1745:
1724:
1712:
1694:
1689:
1686:
1632:
1612:
1604:
1584:
1576:
1554:
1544:
1537:
1520:
1513:
1507:
1487:
1485:
1465:
1457:
1455:
1416:
1414:
1385:
1356:
1352:
1341:
1332:be an arbitrary collection of balls in a
1317:
1315:
1275:
1270:
1265:
1253:
1247:
1222:
1216:
1193:
1188:
1182:
1162:
1139:
1134:
1128:
1107:
1101:
1057:
1033:
1014:
999:
955:
928:
922:
899:
894:
889:
880:
869:
857:
817:
812:
806:
783:
778:
757:
752:
737:
732:
726:
705:
686:
680:
657:
652:
631:
626:
620:
597:
592:
586:
553:
548:
524:
519:
501:
496:
480:
461:
448:
442:
415:
410:
389:
384:
369:
364:
358:
333:
314:
308:
259:
236:
210:
165:
144:
140:
139:
136:
96:
92:
91:
88:
5506:
5493:
4707:is Lebesgue-negligible, for every given
4683:that are not contained in any ball from
3876:of the real line having finite measure.
3438:
3352:The following observation is useful: if
2086:be a maximal disjoint subcollection of
849:and terminate the inductive definition.
5768:, Princeton Lectures in Analysis, III,
5414:
4138:
3791:
1885:be a maximal disjoint subcollection of
1052:. Otherwise, there necessarily is some
5697:Theory of functions of a real variable
5523:
5480:
5425:
5273:, and these balls are disjoint we see
3841:
2976:Now, since increasing the radius of a
63:by a disjoint family extracted from a
5536:
4938:{\displaystyle C_{i}\in \mathbf {G} }
4614:
2512:, defined in the above proof, covers
7:
4026:-dimensional Hausdorff measure, let
2485:, the final value is 1 + 2
2263:intersects a ball from the union of
5556:, Studies in Advanced Mathematics,
5345:goes to infinity, which shows that
4615:infinite form of the covering lemma
4429:with finite Lebesgue measure, then
2527:Hardy–Littlewood maximal inequality
2508:, one shows that the subcollection
1089:{\displaystyle k\in \{1,\dots ,m\}}
5509:), with some notation taken from (
5322:
4825:does not belong to the closed set
4552:
4323:
4320:
4317:
4314:
4231:
4066:a Vitali class of closed sets for
3988:depending only upon the dimension
3886: ≥ 0, to the portion of
3290: > 0, there is a set
2130:
2000:
1988:
1502:are pairwise disjoint, and satisfy
1423:
1420:
1417:
1396:
1363:
1360:
1357:
1308:Theorem (Infinite Covering Lemma).
714:{\displaystyle B_{1},\dots ,B_{n}}
342:{\displaystyle B_{1},\dots ,B_{n}}
14:
4388:coincides with a multiple of the
3632:{\displaystyle {\mathcal {V}}(m)}
3388:, then the subcollection of sets
2215:{\displaystyle B\in \mathbf {F} }
1620:{\displaystyle C\in \mathbf {G} }
1592:{\displaystyle B\in \mathbf {F} }
1439:{\displaystyle \mathrm {rad} (B)}
1157:. We choose the minimal possible
5262:{\displaystyle \mathbf {G} _{r}}
5249:
4931:
4803:{\displaystyle \mathbf {G} _{r}}
4790:
4723:
4625:
3227:a "negligible set", a given set
2678:which is disjoint and such that
2613:{\displaystyle \{B_{j}:j\in J\}}
2516:up to a Lebesgue-negligible set.
2406:
2382:
2343:must have a radius larger than 2
2208:
2137:
2107:
2047:
2026:
2011:
1954:
1924:
1892:(such a subcollection exists by
1805:
1713:
1690:
1613:
1585:
1545:
1521:
1488:
1466:
1458:
1386:
1318:
1211:is at least as large as that of
301:Theorem (Finite Covering Lemma).
153:{\displaystyle \mathbb {R} ^{d}}
105:{\displaystyle \mathbb {R} ^{1}}
4671: > 0 be given, and let
3890:contained in the open annulus Ω
3334:is non-zero and less than
1446:denotes the radius of the ball
5701:Frederick Ungar Publishing Co.
5316:
5303:
5221:
5208:
5166:
5150:
5118:
5112:
4543:
4537:
4517:
4504:
4469:
4455:
4341:
4327:
4297:
4291:
4219:
4205:
4059:{\displaystyle {\mathcal {V}}}
3865:{\displaystyle {\mathcal {V}}}
3717:that is a Vitali covering for
3706:{\displaystyle {\mathcal {V}}}
3626:
3620:
3599:{\displaystyle {\mathcal {V}}}
3573:{\displaystyle {\mathcal {V}}}
3536:
3530:
3504:
3497:
3458:{\displaystyle {\mathcal {V}}}
3409:{\displaystyle {\mathcal {V}}}
3369:{\displaystyle {\mathcal {V}}}
3311:{\displaystyle {\mathcal {V}}}
3267:{\displaystyle {\mathcal {V}}}
3199:
3186:
3139:
3133:
3097:
3084:
3037:
3021:
2957:
2941:
2790:
2784:
2521:Applications and method of use
1756:
1750:
1433:
1427:
1373:
1367:
987:{\displaystyle i=1,2,\dots ,n}
943:{\displaystyle B_{i}\subset X}
279:
264:
188:
176:
83:Visualization of the lemma in
1:
5819:10.1090/S0002-9947-03-03296-3
5812:(8): 3277–3289 (electronic),
5505:The proof given is based on (
5437:The proof given is based on (
5368:on an (infinite-dimensional)
3477:) if there exists a constant
2323:that belongs to the union of
2194:Indeed, if we are given some
1818:{\textstyle \mathbf {F} _{n}}
5599:The geometry of fractal sets
5404:Besicovitch covering theorem
4632:{\displaystyle \mathbf {G} }
3917:Besicovitch covering theorem
2557:{\displaystyle \lambda _{d}}
2259: > 0 and means that
1495:{\displaystyle \mathbf {G} }
1325:{\displaystyle \mathbf {F} }
1177:and note that the radius of
349:be any finite collection of
5641:Encyclopedia of Mathematics
5483:allowed a negligible error.
5353:Infinite-dimensional spaces
5016:{\displaystyle z\in 5C_{i}}
4983:are disjoint, we must have
1649:{\displaystyle B\subset 5C}
834:{\displaystyle B_{j_{k+1}}}
29:combinatorial and geometric
5916:
5764:; Shakarchi, Rami (2005),
5603:Cambridge University Press
3996:of all the given centers.
2351:is less than or equal to 2
1662:Consider the partition of
917:. It remains to show that
5349:is negligible as needed.
4675:denote the set of points
4418:{\displaystyle \{U_{j}\}}
3979:is bounded by a constant
3465:of measurable subsets of
3376:is a Vitali covering for
1204:{\displaystyle B_{j_{k}}}
1150:{\displaystyle B_{j_{k}}}
608:{\displaystyle B_{j_{1}}}
433:of these balls which are
5511:Evans & Gariepy 1992
5469:Evans & Gariepy 1992
5439:Evans & Gariepy 1992
5361:in 1979: there exists a
4380:, the Hausdorff measure
1912:have been selected, let
31:result commonly used in
5874:Vitali covering theorem
5240:But since the balls of
3840:The original result of
3343:Lebesgue negligible set
3219:Vitali covering theorem
2347:. Since the radius of
1480:such that the balls of
224:{\displaystyle c\geq 0}
53:Lebesgue-negligible set
41:Vitali covering theorem
5458:section of this entry.
5332:
5263:
5231:
5079:
5017:
4969:
4968:{\displaystyle 5C_{i}}
4939:
4868:
4804:
4763:
4633:
4590:For every subset E of
4559:
4419:
4363:
4241:
4176:
4107:
4060:
3866:
3831:
3758:
3707:
3633:
3600:
3574:
3543:
3459:
3410:
3370:
3312:
3268:
3209:
3104:
2967:
2758:
2672:
2614:
2558:
2423:
2363:as claimed. From this
2306:intersects a ball in
2216:
2151:
2134:
2067:
1825:consists of the balls
1819:
1788:
1679: ≥ 0, defined by
1650:
1621:
1593:
1565:
1496:
1474:
1440:
1403:
1334:separable metric space
1326:
1293:
1232:
1205:
1171:
1151:
1117:
1090:
1046:
988:
944:
911:
885:
835:
795:
721:that is disjoint from
715:
669:
609:
568:
427:
343:
286:
248:
225:
195:
154:
121:
113:
106:
5868:(Title translation) "
5564:, pp. viii+268,
5333:
5264:
5232:
5088:This gives for every
5080:
5018:
4970:
4940:
4910:intersects some ball
4902:. By the property of
4898:), and disjoint from
4874:by the definition of
4869:
4805:
4764:
4643:such that every ball
4634:
4560:
4420:
4364:
4242:
4177:
4108:
4061:
3867:
3832:
3759:
3708:
3634:
3601:
3575:
3544:
3460:
3411:
3371:
3313:
3269:
3210:
3105:
2968:
2759:
2673:
2615:
2559:
2424:
2293:and by maximality of
2217:
2152:
2114:
2068:
1829:whose radius is in (2
1820:
1789:
1651:
1622:
1594:
1566:
1497:
1475:
1441:
1404:
1327:
1294:
1233:
1231:{\displaystyle B_{i}}
1206:
1172:
1152:
1118:
1116:{\displaystyle B_{i}}
1091:
1047:
989:
945:
912:
865:
836:
796:
716:
670:
610:
569:
428:
344:
287:
249:
226:
196:
194:{\textstyle B=B(x,r)}
155:
119:
107:
82:
75:Vitali covering lemma
25:Vitali covering lemma
5605:, pp. xiv+162,
5595:Falconer, Kenneth J.
5280:
5244:
5099:
5034:
4991:
4949:
4945:and is contained in
4914:
4829:
4785:
4718:
4663: ⊂ 5
4621:
4436:
4396:
4278:
4186:
4117:
4074:
4046:
3950:and positive radius
3852:
3768:
3725:
3693:
3610:
3586:
3560:
3488:
3445:
3396:
3356:
3298:
3254:
3120:
2987:
2771:
2682:
2628:
2579:
2541:
2367:
2198:
2188: ⊂ 5
2103:
2096:. The subcollection
1919:
1800:
1685:
1666:into subcollections
1631:
1603:
1575:
1506:
1484:
1454:
1413:
1340:
1314:
1246:
1215:
1181:
1161:
1127:
1100:
1056:
998:
954:
921:
856:
805:
725:
679:
619:
585:
441:
357:
307:
285:{\textstyle B(x,cr)}
258:
235:
209:
164:
135:
87:
4818:be fixed. For each
4588: —
4016: —
3931:, a Euclidean ball
3679: —
3606:, as is the family
2246:does not belong to
2225:there must be some
1571:And moreover, each
1240:triangle inequality
994:. This is clear if
5677:10.24033/asens.624
5328:
5292:
5259:
5227:
5197:
5139:
5075:
5058:
5013:
4965:
4935:
4864:
4853:
4800:
4759:
4687:and belong to the
4651:intersects a ball
4629:
4586:
4555:
4493:
4448:
4415:
4359:
4312:
4237:
4198:
4172:
4150:
4103:
4056:
4014:
3862:
3827:
3803:
3754:
3703:
3677:
3629:
3596:
3570:
3556:in the collection
3539:
3455:
3406:
3366:
3308:
3294:in the collection
3264:
3205:
3175:
3100:
3073:
3010:
2963:
2930:
2886:
2828:
2754:
2737:
2705:
2668:
2610:
2554:
2419:
2411:
2387:
2319:intersects a ball
2212:
2176:intersects a ball
2147:
2063:
1815:
1784:
1646:
1617:
1589:
1561:
1550:
1526:
1492:
1470:
1436:
1399:
1322:
1289:
1242:then implies that
1228:
1201:
1167:
1147:
1113:
1086:
1042:
984:
940:
907:
831:
791:
711:
665:
605:
581: > 0. Let
564:
423:
339:
282:
247:{\displaystyle cB}
244:
221:
191:
150:
122:
114:
102:
5283:
5269:are contained in
5182:
5124:
5043:
4838:
4484:
4439:
4303:
4189:
4141:
4113:such that either
4006:Hausdorff measure
3794:
3651:, for some fixed
3639:of rectangles in
3473:(in the sense of
3155:
3053:
2990:
2910:
2866:
2813:
2722:
2685:
2394:
2370:
1999:
1996:
1975:
1896:). Assuming that
1748:
1533:
1509:
1170:{\displaystyle k}
55:, a given subset
5907:
5867:
5843:Vitali, Giuseppe
5838:
5821:
5798:
5757:
5719:
5688:
5679:
5649:
5636:"Vitali theorem"
5631:
5590:
5540:
5533:
5527:
5520:
5514:
5503:
5497:
5490:
5484:
5478:
5472:
5465:
5459:
5448:
5442:
5441:, section 1.5.1)
5435:
5429:
5422:
5363:Gaussian measure
5337:
5335:
5334:
5329:
5315:
5314:
5302:
5301:
5291:
5268:
5266:
5265:
5260:
5258:
5257:
5252:
5236:
5234:
5233:
5228:
5220:
5219:
5207:
5206:
5196:
5181:
5180:
5165:
5164:
5149:
5148:
5138:
5111:
5110:
5084:
5082:
5081:
5076:
5071:
5070:
5057:
5022:
5020:
5019:
5014:
5012:
5011:
4974:
4972:
4971:
4966:
4964:
4963:
4944:
4942:
4941:
4936:
4934:
4926:
4925:
4873:
4871:
4870:
4865:
4863:
4862:
4852:
4809:
4807:
4806:
4801:
4799:
4798:
4793:
4768:
4766:
4765:
4760:
4758:
4757:
4748:
4747:
4732:
4731:
4726:
4638:
4636:
4635:
4630:
4628:
4589:
4564:
4562:
4561:
4556:
4536:
4535:
4516:
4515:
4503:
4502:
4492:
4477:
4476:
4467:
4466:
4447:
4424:
4422:
4421:
4416:
4411:
4410:
4368:
4366:
4365:
4360:
4349:
4348:
4339:
4338:
4326:
4311:
4290:
4289:
4250:Furthermore, if
4246:
4244:
4243:
4238:
4227:
4226:
4217:
4216:
4197:
4181:
4179:
4178:
4173:
4165:
4161:
4160:
4159:
4149:
4129:
4128:
4112:
4110:
4109:
4104:
4102:
4101:
4089:
4088:
4065:
4063:
4062:
4057:
4055:
4054:
4017:
3919:. To each point
3871:
3869:
3868:
3863:
3861:
3860:
3836:
3834:
3833:
3828:
3820:
3819:
3813:
3812:
3802:
3787:
3786:
3780:
3779:
3763:
3761:
3760:
3755:
3753:
3752:
3740:
3739:
3712:
3710:
3709:
3704:
3702:
3701:
3680:
3638:
3636:
3635:
3630:
3619:
3618:
3605:
3603:
3602:
3597:
3595:
3594:
3579:
3577:
3576:
3571:
3569:
3568:
3548:
3546:
3545:
3540:
3529:
3528:
3512:
3511:
3464:
3462:
3461:
3456:
3454:
3453:
3415:
3413:
3412:
3407:
3405:
3404:
3375:
3373:
3372:
3367:
3365:
3364:
3317:
3315:
3314:
3309:
3307:
3306:
3273:
3271:
3270:
3265:
3263:
3262:
3214:
3212:
3211:
3206:
3198:
3197:
3185:
3184:
3174:
3173:
3154:
3153:
3132:
3131:
3109:
3107:
3106:
3101:
3096:
3095:
3083:
3082:
3072:
3071:
3052:
3051:
3036:
3035:
3020:
3019:
3009:
3008:
2972:
2970:
2969:
2964:
2956:
2955:
2940:
2939:
2929:
2928:
2906:
2905:
2899:
2898:
2885:
2884:
2865:
2864:
2858:
2857:
2845:
2844:
2838:
2837:
2827:
2812:
2811:
2805:
2804:
2783:
2782:
2763:
2761:
2760:
2755:
2747:
2746:
2736:
2718:
2717:
2704:
2703:
2677:
2675:
2674:
2669:
2667:
2663:
2662:
2645:
2644:
2619:
2617:
2616:
2611:
2594:
2593:
2563:
2561:
2560:
2555:
2553:
2552:
2535:Lebesgue measure
2440:infinite version
2428:
2426:
2425:
2420:
2410:
2409:
2386:
2385:
2315:. In any case,
2255:, which implies
2221:
2219:
2218:
2213:
2211:
2156:
2154:
2153:
2148:
2146:
2145:
2140:
2133:
2128:
2110:
2072:
2070:
2069:
2064:
2056:
2055:
2050:
2035:
2034:
2029:
2020:
2019:
2014:
1997:
1994:
1973:
1969:
1968:
1957:
1939:
1938:
1927:
1824:
1822:
1821:
1816:
1814:
1813:
1808:
1793:
1791:
1790:
1785:
1774:
1773:
1749:
1746:
1738:
1737:
1716:
1699:
1698:
1693:
1655:
1653:
1652:
1647:
1626:
1624:
1623:
1618:
1616:
1599:intersects some
1598:
1596:
1595:
1590:
1588:
1570:
1568:
1567:
1562:
1549:
1548:
1525:
1524:
1501:
1499:
1498:
1493:
1491:
1479:
1477:
1476:
1471:
1469:
1461:
1445:
1443:
1442:
1437:
1426:
1408:
1406:
1405:
1400:
1389:
1366:
1331:
1329:
1328:
1323:
1321:
1303:Infinite version
1298:
1296:
1295:
1290:
1282:
1281:
1280:
1279:
1258:
1257:
1237:
1235:
1234:
1229:
1227:
1226:
1210:
1208:
1207:
1202:
1200:
1199:
1198:
1197:
1176:
1174:
1173:
1168:
1156:
1154:
1153:
1148:
1146:
1145:
1144:
1143:
1122:
1120:
1119:
1114:
1112:
1111:
1095:
1093:
1092:
1087:
1051:
1049:
1048:
1043:
1038:
1037:
1019:
1018:
993:
991:
990:
985:
949:
947:
946:
941:
933:
932:
916:
914:
913:
908:
906:
905:
904:
903:
884:
879:
840:
838:
837:
832:
830:
829:
828:
827:
800:
798:
797:
792:
790:
789:
788:
787:
764:
763:
762:
761:
744:
743:
742:
741:
720:
718:
717:
712:
710:
709:
691:
690:
674:
672:
671:
666:
664:
663:
662:
661:
638:
637:
636:
635:
614:
612:
611:
606:
604:
603:
602:
601:
573:
571:
570:
565:
560:
559:
558:
557:
531:
530:
529:
528:
508:
507:
506:
505:
485:
484:
466:
465:
453:
452:
432:
430:
429:
424:
422:
421:
420:
419:
396:
395:
394:
393:
376:
375:
374:
373:
348:
346:
345:
340:
338:
337:
319:
318:
291:
289:
288:
283:
253:
251:
250:
245:
231:, we will write
230:
228:
227:
222:
200:
198:
197:
192:
159:
157:
156:
151:
149:
148:
143:
111:
109:
108:
103:
101:
100:
95:
37:Euclidean spaces
5915:
5914:
5910:
5909:
5908:
5906:
5905:
5904:
5890:Covering lemmas
5880:
5879:
5841:
5801:
5780:
5762:Stein, Elias M.
5760:
5722:
5703:, p. 277,
5691:
5654:Lebesgue, Henri
5652:
5634:
5613:
5593:
5572:
5551:
5548:
5543:
5534:
5530:
5521:
5517:
5504:
5500:
5491:
5487:
5479:
5475:
5466:
5462:
5449:
5445:
5436:
5432:
5423:
5416:
5412:
5400:
5355:
5306:
5293:
5278:
5277:
5247:
5242:
5241:
5211:
5198:
5172:
5156:
5140:
5102:
5097:
5096:
5092:the inequality
5062:
5032:
5031:
5003:
4989:
4988:
4955:
4947:
4946:
4917:
4912:
4911:
4890:, contained in
4854:
4827:
4826:
4788:
4783:
4782:
4749:
4739:
4721:
4716:
4715:
4619:
4618:
4604:
4587:
4578:
4527:
4507:
4494:
4468:
4458:
4434:
4433:
4402:
4394:
4393:
4340:
4330:
4281:
4276:
4275:
4270:
4248:
4218:
4208:
4184:
4183:
4151:
4134:
4130:
4120:
4115:
4114:
4080:
4072:
4071:
4044:
4043:
4015:
4002:
3987:
3970:
3955:
3944:
3895:
3877:
3850:
3849:
3838:
3804:
3771:
3766:
3765:
3731:
3723:
3722:
3691:
3690:
3678:
3608:
3607:
3584:
3583:
3581:
3558:
3557:
3520:
3503:
3486:
3485:
3443:
3442:
3441:. A collection
3439:Lebesgue (1910)
3436:
3426:
3394:
3393:
3354:
3353:
3296:
3295:
3252:
3251:
3249:Vitali covering
3237:Vitali covering
3221:
3189:
3176:
3166:
3145:
3123:
3118:
3117:
3087:
3074:
3064:
3043:
3027:
3011:
3001:
2985:
2984:
2947:
2931:
2921:
2890:
2877:
2849:
2829:
2796:
2774:
2769:
2768:
2738:
2709:
2696:
2680:
2679:
2655:
2636:
2635:
2631:
2626:
2625:
2585:
2577:
2576:
2544:
2539:
2538:
2523:
2498:Vitali covering
2484:
2365:
2364:
2359: ⊂ 5
2339:. Such a ball
2338:
2329:
2314:
2301:
2292:
2279:
2269:
2254:
2241:
2196:
2195:
2193:
2135:
2101:
2100:
2095:
2085:
2045:
2024:
2009:
1952:
1922:
1917:
1916:
1911:
1902:
1891:
1884:
1877:
1870:
1863:
1854:
1845:
1837:]. A sequence
1803:
1798:
1797:
1762:
1720:
1688:
1683:
1682:
1674:
1629:
1628:
1601:
1600:
1573:
1572:
1504:
1503:
1482:
1481:
1452:
1451:
1411:
1410:
1338:
1337:
1312:
1311:
1305:
1271:
1266:
1249:
1244:
1243:
1218:
1213:
1212:
1189:
1184:
1179:
1178:
1159:
1158:
1135:
1130:
1125:
1124:
1103:
1098:
1097:
1054:
1053:
1029:
1010:
996:
995:
952:
951:
924:
919:
918:
895:
890:
854:
853:
813:
808:
803:
802:
779:
774:
753:
748:
733:
728:
723:
722:
701:
682:
677:
676:
653:
648:
627:
622:
617:
616:
593:
588:
583:
582:
549:
544:
520:
515:
497:
492:
476:
457:
444:
439:
438:
411:
406:
385:
380:
365:
360:
355:
354:
329:
310:
305:
304:
298:
256:
255:
233:
232:
207:
206:
162:
161:
138:
133:
132:
130:Euclidean space
90:
85:
84:
77:
65:Vitali covering
49:Giuseppe Vitali
17:
12:
11:
5:
5913:
5911:
5903:
5902:
5897:
5895:Measure theory
5892:
5882:
5881:
5878:
5877:
5855:(in Italian),
5839:
5799:
5778:
5758:
5720:
5693:Natanson, I. P
5689:
5650:
5632:
5611:
5591:
5570:
5558:Boca Raton, FL
5547:
5544:
5542:
5541:
5528:
5515:
5498:
5485:
5473:
5460:
5443:
5430:
5413:
5411:
5408:
5407:
5406:
5399:
5396:
5354:
5351:
5339:
5338:
5327:
5324:
5321:
5318:
5313:
5309:
5305:
5300:
5296:
5290:
5286:
5256:
5251:
5238:
5237:
5226:
5223:
5218:
5214:
5210:
5205:
5201:
5195:
5192:
5189:
5185:
5179:
5175:
5171:
5168:
5163:
5159:
5155:
5152:
5147:
5143:
5137:
5134:
5131:
5127:
5123:
5120:
5117:
5114:
5109:
5105:
5086:
5085:
5074:
5069:
5065:
5061:
5056:
5053:
5050:
5046:
5042:
5039:
5027:and therefore
5010:
5006:
5002:
4999:
4996:
4975:. But because
4962:
4958:
4954:
4933:
4929:
4924:
4920:
4861:
4857:
4851:
4848:
4845:
4841:
4837:
4834:
4797:
4792:
4756:
4752:
4746:
4742:
4738:
4735:
4730:
4725:
4627:
4582:
4577:
4574:
4566:
4565:
4554:
4551:
4548:
4545:
4542:
4539:
4534:
4530:
4525:
4522:
4519:
4514:
4510:
4506:
4501:
4497:
4491:
4487:
4483:
4480:
4475:
4471:
4465:
4461:
4457:
4454:
4451:
4446:
4442:
4414:
4409:
4405:
4401:
4370:
4369:
4358:
4355:
4352:
4347:
4343:
4337:
4333:
4329:
4325:
4322:
4319:
4316:
4310:
4306:
4302:
4299:
4296:
4293:
4288:
4284:
4266:
4236:
4233:
4230:
4225:
4221:
4215:
4211:
4207:
4204:
4201:
4196:
4192:
4171:
4168:
4164:
4158:
4154:
4148:
4144:
4140:
4137:
4133:
4127:
4123:
4100:
4095:
4092:
4087:
4083:
4079:
4053:
4010:
4001:
3998:
3983:
3966:
3953:
3946:) with center
3942:
3891:
3859:
3848: = 1 and
3826:
3823:
3818:
3811:
3807:
3801:
3797:
3793:
3790:
3785:
3778:
3774:
3751:
3746:
3743:
3738:
3734:
3730:
3700:
3673:
3663:rectangles in
3628:
3625:
3622:
3617:
3593:
3567:
3552:for every set
3550:
3549:
3538:
3535:
3532:
3527:
3523:
3518:
3515:
3510:
3506:
3502:
3499:
3496:
3493:
3471:regular family
3452:
3432:
3425:
3422:
3403:
3363:
3305:
3261:
3220:
3217:
3216:
3215:
3204:
3201:
3196:
3192:
3188:
3183:
3179:
3172:
3169:
3165:
3162:
3158:
3152:
3148:
3144:
3141:
3138:
3135:
3130:
3126:
3111:
3110:
3099:
3094:
3090:
3086:
3081:
3077:
3070:
3067:
3063:
3060:
3056:
3050:
3046:
3042:
3039:
3034:
3030:
3026:
3023:
3018:
3014:
3007:
3004:
3000:
2997:
2993:
2974:
2973:
2962:
2959:
2954:
2950:
2946:
2943:
2938:
2934:
2927:
2924:
2920:
2917:
2913:
2909:
2904:
2897:
2893:
2889:
2883:
2880:
2876:
2873:
2869:
2863:
2856:
2852:
2848:
2843:
2836:
2832:
2826:
2823:
2820:
2816:
2810:
2803:
2799:
2795:
2792:
2789:
2786:
2781:
2777:
2753:
2750:
2745:
2741:
2735:
2732:
2729:
2725:
2721:
2716:
2712:
2708:
2702:
2699:
2695:
2692:
2688:
2666:
2661:
2658:
2654:
2651:
2648:
2643:
2639:
2634:
2609:
2606:
2603:
2600:
2597:
2592:
2588:
2584:
2551:
2547:
2522:
2519:
2518:
2517:
2490:
2480:
2466:
2451:
2418:
2414:
2408:
2404:
2401:
2397:
2393:
2390:
2384:
2380:
2377:
2373:
2334:
2327:
2310:
2297:
2288:
2274:
2267:
2250:
2237:
2210:
2206:
2203:
2158:
2157:
2144:
2139:
2132:
2127:
2124:
2121:
2117:
2113:
2109:
2090:
2080:
2074:
2073:
2062:
2059:
2054:
2049:
2044:
2041:
2038:
2033:
2028:
2023:
2018:
2013:
2008:
2005:
2002:
1993:
1990:
1987:
1984:
1981:
1978:
1972:
1967:
1964:
1961:
1956:
1951:
1948:
1945:
1942:
1937:
1934:
1931:
1926:
1907:
1900:
1889:
1882:
1875:
1868:
1859:
1850:
1841:
1812:
1807:
1783:
1780:
1777:
1772:
1769:
1765:
1761:
1758:
1755:
1752:
1744:
1741:
1736:
1733:
1730:
1727:
1723:
1719:
1715:
1711:
1708:
1705:
1702:
1697:
1692:
1670:
1645:
1642:
1639:
1636:
1615:
1611:
1608:
1587:
1583:
1580:
1560:
1557:
1553:
1547:
1543:
1540:
1536:
1532:
1529:
1523:
1519:
1516:
1512:
1490:
1468:
1464:
1460:
1435:
1432:
1429:
1425:
1422:
1419:
1398:
1395:
1392:
1388:
1384:
1381:
1378:
1375:
1372:
1369:
1365:
1362:
1359:
1355:
1351:
1348:
1345:
1320:
1304:
1301:
1288:
1285:
1278:
1274:
1269:
1264:
1261:
1256:
1252:
1225:
1221:
1196:
1192:
1187:
1166:
1142:
1138:
1133:
1110:
1106:
1085:
1082:
1079:
1076:
1073:
1070:
1067:
1064:
1061:
1041:
1036:
1032:
1028:
1025:
1022:
1017:
1013:
1009:
1006:
1003:
983:
980:
977:
974:
971:
968:
965:
962:
959:
939:
936:
931:
927:
902:
898:
893:
888:
883:
878:
875:
872:
868:
864:
861:
826:
823:
820:
816:
811:
786:
782:
777:
773:
770:
767:
760:
756:
751:
747:
740:
736:
731:
708:
704:
700:
697:
694:
689:
685:
660:
656:
651:
647:
644:
641:
634:
630:
625:
600:
596:
591:
563:
556:
552:
547:
543:
540:
537:
534:
527:
523:
518:
514:
511:
504:
500:
495:
491:
488:
483:
479:
475:
472:
469:
464:
460:
456:
451:
447:
418:
414:
409:
405:
402:
399:
392:
388:
383:
379:
372:
368:
363:
336:
332:
328:
325:
322:
317:
313:
297:
296:Finite version
294:
281:
278:
275:
272:
269:
266:
263:
243:
240:
220:
217:
214:
190:
187:
184:
181:
178:
175:
172:
169:
147:
142:
99:
94:
76:
73:
47:mathematician
33:measure theory
15:
13:
10:
9:
6:
4:
3:
2:
5912:
5901:
5900:Real analysis
5898:
5896:
5893:
5891:
5888:
5887:
5885:
5875:
5871:
5866:
5862:
5858:
5854:
5853:
5848:
5844:
5840:
5837:
5833:
5829:
5825:
5820:
5815:
5811:
5807:
5806:
5800:
5797:
5793:
5789:
5785:
5781:
5779:0-691-11386-6
5775:
5771:
5770:Princeton, NJ
5767:
5763:
5759:
5756:
5752:
5748:
5744:
5740:
5736:
5732:
5728:
5727:
5721:
5718:
5714:
5710:
5706:
5702:
5698:
5694:
5690:
5687:
5683:
5678:
5673:
5669:
5665:
5664:
5659:
5655:
5651:
5647:
5643:
5642:
5637:
5633:
5630:
5626:
5622:
5618:
5614:
5612:0-521-25694-1
5608:
5604:
5600:
5596:
5592:
5589:
5585:
5581:
5577:
5573:
5571:0-8493-7157-0
5567:
5563:
5559:
5555:
5550:
5549:
5545:
5538:
5532:
5529:
5525:
5519:
5516:
5512:
5508:
5507:Natanson 1955
5502:
5499:
5495:
5494:Falconer 1986
5489:
5486:
5482:
5481:Vitali (1908)
5477:
5474:
5470:
5464:
5461:
5457:
5455:
5447:
5444:
5440:
5434:
5431:
5427:
5421:
5419:
5415:
5409:
5405:
5402:
5401:
5397:
5395:
5393:
5389:
5385:
5382:, Borel(
5381:
5377:
5374:
5373:Hilbert space
5371:
5367:
5364:
5360:
5352:
5350:
5348:
5344:
5325:
5319:
5311:
5307:
5298:
5294:
5288:
5284:
5276:
5275:
5274:
5272:
5254:
5224:
5216:
5212:
5203:
5199:
5193:
5190:
5187:
5183:
5177:
5173:
5169:
5161:
5157:
5153:
5145:
5141:
5135:
5132:
5129:
5125:
5121:
5115:
5107:
5103:
5095:
5094:
5093:
5091:
5072:
5067:
5063:
5059:
5054:
5051:
5048:
5044:
5040:
5037:
5030:
5029:
5028:
5026:
5008:
5004:
5000:
4997:
4994:
4986:
4982:
4978:
4960:
4956:
4952:
4927:
4922:
4918:
4909:
4905:
4901:
4897:
4893:
4889:
4885:
4881:
4877:
4859:
4855:
4849:
4846:
4843:
4839:
4835:
4832:
4824:
4821:
4817:
4813:
4795:
4781:). Note that
4780:
4776:
4772:
4754:
4744:
4740:
4733:
4728:
4712:
4710:
4706:
4702:
4698:
4694:
4690:
4686:
4682:
4678:
4674:
4670:
4666:
4662:
4658:
4654:
4650:
4646:
4642:
4616:
4612:
4608:
4603:
4601:
4597:
4593:
4581:
4575:
4573:
4571:
4549:
4546:
4540:
4532:
4528:
4523:
4520:
4512:
4508:
4499:
4495:
4489:
4485:
4481:
4478:
4473:
4463:
4459:
4452:
4449:
4444:
4440:
4432:
4431:
4430:
4428:
4407:
4403:
4391:
4387:
4383:
4379:
4375:
4356:
4353:
4350:
4345:
4335:
4331:
4308:
4304:
4300:
4294:
4286:
4282:
4274:
4273:
4272:
4269:
4265:
4261:
4257:
4253:
4247:
4234:
4228:
4223:
4213:
4209:
4202:
4199:
4194:
4190:
4169:
4166:
4162:
4156:
4152:
4146:
4142:
4135:
4131:
4125:
4121:
4093:
4085:
4081:
4069:
4041:
4037:
4033:
4030: ⊆
4029:
4025:
4021:
4009:
4007:
3997:
3995:
3991:
3986:
3982:
3978:
3975: ∈
3974:
3969:
3965:
3960:
3956:
3949:
3945:
3938:
3934:
3930:
3927: ⊆
3926:
3922:
3918:
3913:
3911:
3907:
3903:
3899:
3894:
3889:
3885:
3881:
3875:
3847:
3843:
3842:Vitali (1908)
3837:
3824:
3821:
3809:
3805:
3799:
3795:
3788:
3776:
3772:
3744:
3736:
3732:
3720:
3716:
3688:
3685: ⊆
3684:
3672:
3670:
3666:
3662:
3658:
3654:
3650:
3646:
3642:
3623:
3555:
3533:
3525:
3521:
3516:
3513:
3508:
3500:
3494:
3491:
3484:
3483:
3482:
3480:
3476:
3472:
3468:
3440:
3435:
3431:
3421:
3419:
3391:
3387:
3383:
3379:
3350:
3348:
3344:
3339:
3337:
3333:
3329:
3325:
3322: ∈
3321:
3293:
3289:
3285:
3282: ∈
3281:
3277:
3250:
3246:
3242:
3238:
3234:
3231: ⊆
3230:
3226:
3218:
3202:
3194:
3190:
3181:
3177:
3170:
3167:
3163:
3160:
3156:
3150:
3146:
3142:
3136:
3128:
3124:
3116:
3115:
3114:
3092:
3088:
3079:
3075:
3068:
3065:
3061:
3058:
3054:
3048:
3044:
3040:
3032:
3028:
3024:
3016:
3012:
3005:
3002:
2998:
2995:
2991:
2983:
2982:
2981:
2979:
2960:
2952:
2948:
2944:
2936:
2932:
2925:
2922:
2918:
2915:
2911:
2907:
2895:
2891:
2887:
2881:
2878:
2874:
2871:
2867:
2854:
2850:
2846:
2834:
2830:
2824:
2821:
2818:
2814:
2801:
2797:
2793:
2787:
2779:
2775:
2767:
2766:
2765:
2764:. Therefore,
2751:
2748:
2743:
2739:
2733:
2730:
2727:
2723:
2719:
2714:
2710:
2706:
2700:
2697:
2693:
2690:
2686:
2664:
2659:
2656:
2652:
2649:
2646:
2641:
2637:
2632:
2623:
2604:
2601:
2598:
2595:
2590:
2586:
2574:
2570:
2567:
2549:
2545:
2536:
2533:-dimensional
2532:
2528:
2520:
2515:
2511:
2507:
2503:
2499:
2495:
2491:
2488:
2483:
2479:
2475:
2471:
2467:
2464:
2461:, and 5
2460:
2456:
2452:
2449:
2445:
2441:
2437:
2436:
2435:
2434:
2430:
2416:
2412:
2402:
2399:
2395:
2391:
2388:
2378:
2375:
2371:
2362:
2358:
2354:
2350:
2346:
2342:
2337:
2333:
2326:
2322:
2318:
2313:
2309:
2305:
2300:
2296:
2291:
2287:
2283:
2277:
2273:
2266:
2262:
2258:
2253:
2249:
2245:
2240:
2236:
2232:
2229:be such that
2228:
2224:
2204:
2201:
2191:
2187:
2183:
2179:
2175:
2171:
2167:
2163:
2142:
2125:
2122:
2119:
2115:
2111:
2099:
2098:
2097:
2093:
2089:
2083:
2079:
2060:
2052:
2042:
2039:
2036:
2031:
2021:
2016:
2006:
2003:
1991:
1985:
1982:
1979:
1976:
1970:
1965:
1962:
1959:
1949:
1946:
1940:
1935:
1932:
1929:
1915:
1914:
1913:
1910:
1906:
1899:
1895:
1888:
1881:
1874:
1867:
1862:
1858:
1853:
1849:
1844:
1840:
1836:
1832:
1828:
1810:
1794:
1781:
1775:
1770:
1767:
1763:
1759:
1753:
1742:
1739:
1734:
1731:
1728:
1725:
1721:
1717:
1709:
1706:
1700:
1695:
1680:
1678:
1673:
1669:
1665:
1661:
1657:
1643:
1640:
1637:
1634:
1609:
1606:
1581:
1578:
1558:
1555:
1551:
1541:
1538:
1534:
1530:
1527:
1517:
1514:
1510:
1462:
1449:
1430:
1393:
1382:
1379:
1376:
1370:
1346:
1343:
1335:
1309:
1302:
1300:
1286:
1283:
1276:
1272:
1267:
1262:
1259:
1254:
1250:
1241:
1223:
1219:
1194:
1190:
1185:
1164:
1140:
1136:
1131:
1108:
1104:
1080:
1077:
1074:
1071:
1068:
1062:
1059:
1034:
1030:
1026:
1023:
1020:
1015:
1011:
1004:
1001:
981:
978:
975:
972:
969:
966:
963:
960:
957:
937:
934:
929:
925:
900:
896:
891:
886:
881:
876:
873:
870:
866:
862:
859:
850:
848:
844:
824:
821:
818:
814:
809:
784:
780:
775:
771:
768:
765:
758:
754:
749:
745:
738:
734:
729:
706:
702:
698:
695:
692:
687:
683:
658:
654:
649:
645:
642:
639:
632:
628:
623:
598:
594:
589:
580:
576:
561:
554:
550:
545:
541:
538:
535:
532:
525:
521:
516:
512:
509:
502:
498:
493:
489:
486:
481:
477:
473:
470:
467:
462:
458:
454:
449:
445:
436:
416:
412:
407:
403:
400:
397:
390:
386:
381:
377:
370:
366:
361:
352:
334:
330:
326:
323:
320:
315:
311:
302:
295:
293:
276:
273:
270:
267:
261:
254:for the ball
241:
238:
218:
215:
212:
204:
185:
182:
179:
173:
170:
167:
145:
131:
127:
118:
97:
81:
74:
72:
70:
66:
62:
58:
54:
50:
46:
42:
38:
34:
30:
26:
22:
5869:
5856:
5850:
5809:
5803:
5765:
5733:(1): 95–99,
5730:
5724:
5699:, New York:
5696:
5667:
5661:
5639:
5598:
5553:
5531:
5518:
5501:
5488:
5476:
5463:
5453:
5446:
5433:
5391:
5387:
5383:
5379:
5375:
5365:
5359:David Preiss
5356:
5346:
5342:
5340:
5270:
5239:
5089:
5087:
5024:
4984:
4980:
4976:
4907:
4903:
4899:
4895:
4891:
4887:
4883:
4879:
4875:
4822:
4819:
4815:
4811:
4778:
4774:
4770:
4713:
4708:
4704:
4700:
4699:) of radius
4696:
4692:
4688:
4684:
4680:
4676:
4672:
4668:
4664:
4660:
4656:
4652:
4648:
4644:
4640:
4610:
4606:
4605:
4599:
4595:
4591:
4583:
4579:
4569:
4567:
4426:
4389:
4385:
4381:
4377:
4373:
4371:
4271:} such that
4267:
4263:
4259:
4255:
4251:
4249:
4067:
4035:
4031:
4027:
4023:
4019:
4011:
4003:
3993:
3989:
3984:
3980:
3976:
3972:
3967:
3963:
3958:
3951:
3947:
3940:
3936:
3932:
3928:
3924:
3923:of a subset
3920:
3914:
3909:
3908:| <
3905:
3904: < |
3901:
3897:
3892:
3887:
3883:
3879:
3873:
3845:
3839:
3718:
3714:
3686:
3682:
3674:
3668:
3664:
3660:
3656:
3652:
3648:
3644:
3640:
3553:
3551:
3478:
3470:
3466:
3433:
3429:
3427:
3417:
3389:
3385:
3381:
3377:
3351:
3346:
3342:
3340:
3335:
3331:
3323:
3319:
3291:
3287:
3283:
3279:
3275:
3248:
3245:Vitali class
3244:
3240:
3236:
3232:
3228:
3224:
3222:
3112:
2977:
2975:
2621:
2572:
2568:
2530:
2524:
2513:
2509:
2505:
2501:
2500:of a subset
2497:
2493:
2486:
2481:
2477:
2473:
2469:
2462:
2458:
2454:
2439:
2432:
2431:
2360:
2356:
2352:
2348:
2344:
2340:
2335:
2331:
2324:
2320:
2316:
2311:
2307:
2303:
2298:
2294:
2289:
2285:
2281:
2275:
2271:
2264:
2260:
2256:
2251:
2247:
2243:
2238:
2234:
2230:
2226:
2222:
2189:
2185:
2181:
2177:
2173:
2169:
2165:
2161:
2159:
2091:
2087:
2081:
2077:
2075:
1908:
1904:
1897:
1894:Zorn's lemma
1886:
1879:
1872:
1865:
1860:
1856:
1851:
1847:
1842:
1838:
1834:
1830:
1826:
1795:
1681:
1676:
1671:
1667:
1663:
1659:
1658:
1447:
1307:
1306:
851:
846:
842:
578:
574:
437:and satisfy
300:
299:
126:metric space
123:
68:
64:
60:
56:
40:
24:
18:
5670:: 361–450,
5524:Preiss 1979
5426:Vitali 1908
4906:, the ball
4886:containing
4254:has finite
2448:uncountable
2233:belongs to
1123:intersects
21:mathematics
5884:Categories
5865:39.0101.05
5836:1042.28014
5796:1081.28001
5755:0386.28015
5717:0064.29102
5686:41.0457.01
5629:0587.28004
5588:0804.28001
5546:References
5537:Tišer 2003
4773:that meet
4659:for which
4040:measurable
3900:such that
3896:of points
3764:such that
3481:such that
3437:is due to
3318:such that
3243: : a
2242:. Either
2184:such that
1336:such that
1096:such that
950:for every
5859:: 75–92,
5845:(1908) ,
5739:0010-2628
5646:EMS Press
5562:CRC Press
5370:separable
5323:∞
5295:λ
5285:∑
5200:λ
5184:∑
5142:λ
5126:∑
5122:≤
5104:λ
5045:⋃
5041:⊂
5025:i > N,
5023:for some
4998:∈
4985:i > N.
4928:∈
4847:≤
4840:⋃
4553:∞
4529:λ
4521:≤
4496:λ
4486:∑
4479:≤
4453:
4441:∑
4354:ε
4305:∑
4301:≤
4232:∞
4203:
4191:∑
4143:⋃
4139:∖
4094:⊆
3796:⋃
3792:∖
3773:λ
3745:⊆
3671:regular.
3522:λ
3514:≤
3495:
3239:for
3178:λ
3164:∈
3157:∑
3143:≤
3125:λ
3113:and thus
3076:λ
3062:∈
3055:∑
3013:λ
2999:∈
2992:∑
2933:λ
2919:∈
2912:∑
2908:≤
2875:∈
2868:⋃
2851:λ
2847:≤
2822:∈
2815:⋃
2798:λ
2794:≤
2776:λ
2749:⊃
2731:∈
2724:⋃
2720:⊃
2694:∈
2687:⋃
2653:∈
2602:∈
2546:λ
2444:countable
2403:∈
2396:⋃
2392:⊆
2379:∈
2372:⋃
2205:∈
2131:∞
2116:⋃
2043:∪
2040:⋯
2037:∪
2022:∪
2007:∈
2001:∀
1989:∅
1980:∩
1950:∈
1796:That is,
1768:−
1760:≤
1732:−
1726:−
1710:∈
1638:⊂
1610:∈
1582:∈
1542:∈
1535:⋃
1531:⊆
1518:∈
1511:⋃
1463:⊂
1397:∞
1383:∈
1284:⊂
1260:⊂
1075:…
1063:∈
1024:…
1005:∈
976:…
935:⊂
867:⋃
845: :=
772:∪
769:⋯
766:∪
746:∪
696:…
643:…
539:∪
536:⋯
533:∪
510:∪
487:⊆
474:∪
471:⋯
468:∪
455:∪
401:…
324:…
216:≥
5695:(1955),
5656:(1910),
5597:(1986),
5450:See the
5398:See also
5386:),
4882: ∈
4814: ∈
4679: ∈
4655: ∈
4647: ∈
4376: =
4042:set and
3475:Lebesgue
3328:diameter
3326:and the
3171:′
3069:′
3006:′
2926:′
2882:′
2701:′
2660:′
2571: ⊂
2284: ∈
2180: ∈
2172: ∈
2076:and let
1878:and let
1871: =
1855: ⊂
852:Now set
435:disjoint
5828:1974687
5788:2129625
5747:0526149
5709:0067952
5648:, 2001
5621:0867284
5580:1158660
4585:Theorem
4022:denote
4013:Theorem
3939:,
3676:Theorem
3380:and if
2564:, of a
2438:In the
2433:Remarks
2330:, ...,
2270:, ...,
1846:, with
45:Italian
5863:
5834:
5826:
5794:
5786:
5776:
5753:
5745:
5737:
5715:
5707:
5684:
5627:
5619:
5609:
5586:
5578:
5568:
5271:B(r+2)
4667:. Let
4607:Proof:
4034:be an
1998:
1995:
1974:
1660:Proof:
1409:where
1238:. The
801:, let
575:Proof:
23:, the
5467:See (
5410:Notes
5392:every
4691:ball
3469:is a
3225:up to
2496:is a
2280:, or
1903:,...,
1627:with
351:balls
201:is a
27:is a
5774:ISBN
5735:ISSN
5607:ISBN
5566:ISBN
5320:<
5191:>
5133:>
5052:>
4979:and
4714:Let
4689:open
4547:<
4450:diam
4200:diam
4018:Let
3912:+1.
3681:Let
3647:and
3492:diam
3286:and
3274:for
1743:<
1394:<
1310:Let
303:Let
205:and
203:ball
5861:JFM
5832:Zbl
5814:doi
5810:355
5792:Zbl
5751:Zbl
5713:Zbl
5682:JFM
5672:doi
5625:Zbl
5584:Zbl
4987:So
4639:of
4384:on
4182:or
3669:not
3667:is
3661:all
3392:in
3330:of
3247:or
2566:set
2504:of
2446:or
2160:of
1833:, 2
1747:rad
1350:sup
67:of
59:of
35:of
19:In
5886::
5857:43
5849:,
5830:,
5824:MR
5822:,
5808:,
5790:,
5784:MR
5782:,
5749:,
5743:MR
5741:,
5731:20
5729:,
5711:,
5705:MR
5680:,
5668:27
5666:,
5660:,
5644:,
5638:,
5623:,
5617:MR
5615:,
5582:,
5576:MR
5574:,
5560::
5539:).
5526:).
5513:).
5496:).
5471:).
5428:).
5417:^
4820:N,
4711:.
3825:0.
3420:.
3338:.
2537:,
2472:,
2361:C,
2353:R,
2302:,
2278:−1
2112::=
2094:+1
2084:+1
1675:,
1656:.
1347::=
863::=
292:.
71:.
5876:.
5816::
5674::
5535:(
5522:(
5492:(
5456:"
5452:"
5424:(
5388:γ
5384:H
5380:H
5376:H
5366:γ
5347:Z
5343:N
5326:.
5317:)
5312:n
5308:C
5304:(
5299:d
5289:n
5255:r
5250:G
5225:.
5222:)
5217:n
5213:C
5209:(
5204:d
5194:N
5188:n
5178:d
5174:5
5170:=
5167:)
5162:n
5158:C
5154:5
5151:(
5146:d
5136:N
5130:n
5119:)
5116:Z
5113:(
5108:d
5090:N
5073:.
5068:n
5064:C
5060:5
5055:N
5049:n
5038:Z
5009:i
5005:C
5001:5
4995:z
4981:B
4977:K
4961:i
4957:C
4953:5
4932:G
4923:i
4919:C
4908:B
4904:G
4900:K
4896:r
4894:(
4892:B
4888:z
4884:F
4880:B
4876:Z
4860:n
4856:C
4850:N
4844:n
4836:=
4833:K
4823:z
4816:Z
4812:z
4796:r
4791:G
4779:r
4777:(
4775:B
4771:G
4755:n
4751:}
4745:n
4741:C
4737:{
4734:=
4729:r
4724:G
4709:r
4705:Z
4701:r
4697:r
4695:(
4693:B
4685:G
4681:E
4677:z
4673:Z
4669:r
4665:C
4661:B
4657:G
4653:C
4649:F
4645:B
4641:F
4626:G
4611:F
4600:G
4596:F
4592:R
4570:E
4550:+
4544:)
4541:B
4538:(
4533:d
4524:C
4518:)
4513:j
4509:U
4505:(
4500:d
4490:j
4482:C
4474:d
4470:)
4464:j
4460:U
4456:(
4445:j
4427:B
4413:}
4408:j
4404:U
4400:{
4390:d
4386:R
4382:H
4378:d
4374:s
4357:.
4351:+
4346:s
4342:)
4336:j
4332:U
4328:(
4324:m
4321:a
4318:i
4315:d
4309:j
4298:)
4295:E
4292:(
4287:s
4283:H
4268:j
4264:U
4260:ε
4256:s
4252:E
4235:.
4229:=
4224:s
4220:)
4214:j
4210:U
4206:(
4195:j
4170:0
4167:=
4163:)
4157:j
4153:U
4147:j
4136:E
4132:(
4126:s
4122:H
4099:V
4091:}
4086:j
4082:U
4078:{
4068:E
4052:V
4038:-
4036:H
4032:R
4028:E
4024:s
4020:H
3994:A
3990:d
3985:d
3981:B
3977:R
3973:x
3968:x
3964:N
3959:A
3954:a
3952:r
3948:a
3943:a
3941:r
3937:a
3935:(
3933:B
3929:R
3925:A
3921:a
3910:n
3906:x
3902:n
3898:x
3893:n
3888:E
3884:n
3880:E
3874:E
3858:V
3846:d
3822:=
3817:)
3810:j
3806:U
3800:j
3789:E
3784:(
3777:d
3750:V
3742:}
3737:j
3733:U
3729:{
3719:E
3715:R
3699:V
3687:R
3683:E
3665:R
3657:R
3653:m
3649:m
3645:m
3641:R
3627:)
3624:m
3621:(
3616:V
3592:V
3580:.
3566:V
3554:V
3537:)
3534:V
3531:(
3526:d
3517:C
3509:d
3505:)
3501:V
3498:(
3479:C
3467:R
3451:V
3434:d
3430:λ
3418:E
3402:V
3390:U
3386:R
3382:E
3378:E
3362:V
3347:R
3336:δ
3332:U
3324:U
3320:x
3304:V
3292:U
3288:δ
3284:E
3280:x
3276:E
3260:V
3241:E
3233:R
3229:E
3203:.
3200:)
3195:j
3191:B
3187:(
3182:d
3168:J
3161:j
3151:d
3147:5
3140:)
3137:E
3134:(
3129:d
3098:)
3093:j
3089:B
3085:(
3080:d
3066:J
3059:j
3049:d
3045:5
3041:=
3038:)
3033:j
3029:B
3025:5
3022:(
3017:d
3003:J
2996:j
2978:d
2961:.
2958:)
2953:j
2949:B
2945:5
2942:(
2937:d
2923:J
2916:j
2903:)
2896:j
2892:B
2888:5
2879:J
2872:j
2862:(
2855:d
2842:)
2835:j
2831:B
2825:J
2819:j
2809:(
2802:d
2791:)
2788:E
2785:(
2780:d
2752:E
2744:j
2740:B
2734:J
2728:j
2715:j
2711:B
2707:5
2698:J
2691:j
2665:}
2657:J
2650:j
2647::
2642:j
2638:B
2633:{
2622:E
2608:}
2605:J
2599:j
2596::
2591:j
2587:B
2583:{
2573:R
2569:E
2550:d
2531:d
2514:E
2510:G
2506:R
2502:E
2494:F
2487:c
2482:n
2478:F
2474:c
2470:c
2463:B
2459:B
2455:R
2417:C
2413:5
2407:G
2400:C
2389:B
2383:F
2376:B
2357:B
2349:B
2345:R
2341:C
2336:n
2332:G
2328:0
2325:G
2321:C
2317:B
2312:n
2308:G
2304:B
2299:n
2295:G
2290:n
2286:H
2282:B
2276:n
2272:G
2268:0
2265:G
2261:B
2257:n
2252:n
2248:H
2244:B
2239:n
2235:F
2231:B
2227:n
2223:,
2209:F
2202:B
2192:.
2190:C
2186:B
2182:G
2178:C
2174:F
2170:B
2166:G
2162:F
2143:n
2138:G
2126:0
2123:=
2120:n
2108:G
2092:n
2088:H
2082:n
2078:G
2061:,
2058:}
2053:n
2048:G
2032:1
2027:G
2017:0
2012:G
2004:C
1992:,
1986:=
1983:C
1977:B
1971::
1966:1
1963:+
1960:n
1955:F
1947:B
1944:{
1941:=
1936:1
1933:+
1930:n
1925:H
1909:n
1905:G
1901:0
1898:G
1890:0
1887:H
1883:0
1880:G
1876:0
1873:F
1869:0
1866:H
1861:n
1857:F
1852:n
1848:G
1843:n
1839:G
1835:R
1831:R
1827:B
1811:n
1806:F
1782:.
1779:}
1776:R
1771:n
1764:2
1757:)
1754:B
1751:(
1740:R
1735:1
1729:n
1722:2
1718::
1714:F
1707:B
1704:{
1701:=
1696:n
1691:F
1677:n
1672:n
1668:F
1664:F
1644:C
1641:5
1635:B
1614:G
1607:C
1586:F
1579:B
1559:.
1556:C
1552:5
1546:G
1539:C
1528:B
1522:F
1515:B
1489:G
1467:F
1459:G
1448:B
1434:)
1431:B
1428:(
1424:d
1421:a
1418:r
1391:}
1387:F
1380:B
1377::
1374:)
1371:B
1368:(
1364:d
1361:a
1358:r
1354:{
1344:R
1319:F
1287:X
1277:k
1273:j
1268:B
1263:3
1255:i
1251:B
1224:i
1220:B
1195:k
1191:j
1186:B
1165:k
1141:k
1137:j
1132:B
1109:i
1105:B
1084:}
1081:m
1078:,
1072:,
1069:1
1066:{
1060:k
1040:}
1035:m
1031:j
1027:,
1021:,
1016:1
1012:j
1008:{
1002:i
982:n
979:,
973:,
970:2
967:,
964:1
961:=
958:i
938:X
930:i
926:B
901:k
897:j
892:B
887:3
882:m
877:1
874:=
871:k
860:X
847:k
843:m
825:1
822:+
819:k
815:j
810:B
785:k
781:j
776:B
759:2
755:j
750:B
739:1
735:j
730:B
707:n
703:B
699:,
693:,
688:1
684:B
659:k
655:j
650:B
646:,
640:,
633:1
629:j
624:B
599:1
595:j
590:B
579:n
562:.
555:m
551:j
546:B
542:3
526:2
522:j
517:B
513:3
503:1
499:j
494:B
490:3
482:n
478:B
463:2
459:B
450:1
446:B
417:m
413:j
408:B
404:,
398:,
391:2
387:j
382:B
378:,
371:1
367:j
362:B
335:n
331:B
327:,
321:,
316:1
312:B
280:)
277:r
274:c
271:,
268:x
265:(
262:B
242:B
239:c
219:0
213:c
189:)
186:r
183:,
180:x
177:(
174:B
171:=
168:B
146:d
141:R
112:.
98:1
93:R
69:E
61:R
57:E
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.