1182:
the wheel to avoid redundant culls; some optimizations may be able to be made based on the fact that (will be proven in the next section) that there will be no repeat culling of any composite number: each remaining composite will be culled exactly once. Alternatively, one can continue to generate truncated wheel lists using primes up to the square root of the desired sieve range, in which case all remaining number representations in the wheel will be prime; however, although this method is as efficient as to never culling composite numbers more than once, it loses much time external to the normally considered culling operations in processing the successive wheel sweeps so as to take much longer. The elimination of composite numbers by a factorization wheel is based on the following: Given a number
81:
919:
1165:
previous 2/3 factorization wheel. One could then follow the steps to step 10 using the next succeeding prime of 7 cycles and only eliminating the multiples of 7 from the resulting list in step 10 (leaving some "relative" primes in this case and all successive cases - i.e. some not true fully qualified primes), to get the next further advanced wheel, recursively repeating the steps as necessary to get successively larger wheels.
25:
810:. Because not all the numbers in these lists are prime, doing so introduces inefficient redundant operations. However, the generators themselves require very little memory compared to keeping a pure list of prime numbers. The small list of initial prime numbers constitute complete parameters for the
1181:
Note that once a wheel spans the desired upper limit of the sieving range, one can stop generating further wheels and use the information in that wheel to cull the remaining composite numbers from that last wheel list using a Sieve of
Eratosthenes type technique but using the gap pattern inherent to
1164:
Note that by using exactly the next prime number of 5 wheel cycles and eliminating the multiple(s) of that prime (and only that prime) from the resulting list, we have obtained the base wheel as per step 4 for a factorization wheel with base primes of 2, 3, and 5; this is one wheel in advance of the
615:
For getting the complete factorization of an integer, the computation may be continued without restarting the wheel at the beginning. This leads to the following program for a complete factorization, where the function "add" adds its first argument at the end of the second argument, which must be a
825:
to generate more accurate wheels. Much definitive work on wheel factorization, sieves using wheel factorization, and wheel sieve, was done by Paul
Pritchard in formulating a series of different algorithms. To visualize the use of a factorization wheel, one may start by writing the natural numbers
1177:
As seen in the example above, the result of repeated applications of the above recursive procedure from steps 4 to 10 can be a wheel list which spans any desired sieving range (to which it can be truncated) and the resulting list then includes only the multiples of primes higher than one past the
1173:
Formally, the method makes use of the following insights: First, that the set of base primes unioned with its (infinite) set of coprimes is a superset of the primes. Second, that the infinite set of coprimes can be enumerated easily from the coprimes to the base set between 2 and the base set
161:
in the basis as their possible factors. It is as if these generated numbers have already been tested, and found to not be divisible by any of the primes in the basis. It is an optimization because all these operations become redundant, and are spared from being performed at all.
861:
in the innermost circle, strike off all multiples of the base primes from step one as applied in step 2. This composite number elimination can be accomplished either by use of a sieve such as the Sieve of
Eratosthenes or as the result of applications of smaller factorization
1347:. Thus phi(n) / n goes to zero slowly as n increases to infinity and it can be seen that this efficiency rises very slowly to 100% for infinitely large n. From the properties of phi, it can easily be seen that the most efficient sieve smaller than x is the one where
1228:
are not relatively prime. From that, the fraction of numbers that the wheel sieve eliminates can be determined (although not all need be physically struck off; many can be culled automatically in the operations of copying of lesser wheels to greater wheels) as
908:
The remaining numbers in the wheel are mostly prime numbers (they are collectively called "relatively" prime). Use other methods such as the Sieve of
Eratosthenes or further application of larger factorization wheels to remove the remaining
1334:
134:
The trial division method consists of dividing the number to be factorized by the integers in increasing order (2, 3, 4, 5, ...) successively. A common improvement consists of testing only by primes, i.e. by 2, 3, 5, 7, 11, ... .
347:
between the consecutive numbers, and then generating the sequence starting from 1 by repeatedly adding these increments one after another to the last generated number, indefinitely. This is the closest it comes to the
2705:
835:
Find the first few prime numbers to form the basis of the factorization wheel. They are known or perhaps determined from previous applications of smaller factorization wheels or by quickly finding them using the
2040:, reducing storage requirements. The following algorithm does not use this fact, but it is based on the fact that the gaps between successive numbers in each set are symmetrical around the halfway point.
119:
primes determine the specific way to generate a sequence of natural numbers which are all known in advance to be coprime with these primes, i.e. are all known to not be multiples of any of these primes.
240:
Every second number in these triplets will be a multiple of 3, because numbers of the form 3 + 6k are all odd multiples of 3. Thus all the numbers coprime with the first two primes i.e. 2 and 3, i.e. 2
1983:
removing the need to compute prime numbers separately although the algorithm does need to keep a record of all eliminated base primes which are no longer included in the succeeding sets.
2709:
1413:
1865:
902:
Strike off the spokes of the prime numbers as found in step 1 and applied in step 2 in all outer circles without striking off the prime numbers in the inner-most circle (in circle 1).
1460:
To be of maximum use on a computer, we want the numbers that are smaller than n and relatively prime to it as a set. Using a few observations, the set can easily be generated :
2217:
1455:
1614:
188:
The bigger the wheel the larger the computational resources involved and the smaller the additional improvements, though, so it is the case of quickly diminishing returns.
1569:
1501:
905:
Strike off the spokes of all multiples of prime numbers struck from the inner circle 1 in step 4 in the same way as striking off the spokes of the base primes in step 8.
826:
around circles as shown in the adjacent diagram. The number of spokes is chosen such that prime numbers will have a tendency to accumulate in a minority of the spokes.
2250:
1928:
1650:
2010:
1981:
1208:
91:
is a method for generating a sequence of natural numbers by repeated additions, as determined by a number of the first few primes, so that the generated numbers are
1955:
1892:
1677:
2038:
1527:
1529:
with 2 as the first prime. This initial set means that all numbers starting at two up are included as "relative" primes as the circumference of the wheel is 1.
1255:
305:{1} (containing one i.e. (2−1) number) with the "circumference" of 2 for generating the sequence of 2–coprimes i.e. odds by repeated addition of 2;
2574:
2210:
2154:
177:
of all the candidate numbers are skipped over automatically. Larger bases reduce this proportion even further; for example, with basis {2, 3, 5} to
1457:(i.e. wheel generation can stop when the last wheel passes or has a sufficient circumference to include the highest number in the sieving range).
169:
in general, this method reduces the amount of candidate numbers to be considered as possible primes. With the basis {2, 3}, the reduction is to
2442:
2167:
2384:
2203:
49:
2313:
2490:
2288:
67:
2399:
355:
For instance, this turns {1, 7, 11, 13, 17, 19, 23, 29, 31} into {6, 4, 2, 4, 2, 4, 6, 2}, and then the sequence is generated as
2437:
2374:
2318:
2281:
1156:
The resulting list contains a non-prime number of 25 which is 5. Use other methods such as a sieve to eliminate it to arrive at
2579:
2470:
2389:
2379:
2255:
2407:
288:
Out of each ten of these 6–coprime numbers, two are multiples of 5, thus the remaining eight will be 30–coprime:
45:
The computer implementation algorithm, pseudocode, further performance analysis, and computation complexity are not complete.
2660:
1344:
2655:
2584:
2485:
818:. While each wheel may generate an infinite list of numbers, past a certain point the numbers cease to be mostly prime.
2622:
1616:
has the factors of 2 and 3 eliminated (circumference of 6) as for the initial base wheel in the example above and so on.
802:
from a simple mathematical formula and a much smaller list of the first prime numbers. These lists may then be used in
2536:
433:
For implementing the method, one may remark that the increments between two consecutive elements of the wheel, that is
430:
of the basis, to the numbers in the first turn. The third turn is obtained by adding 30 to the second turn, and so on.
40:
2189:
1232:
2701:
2691:
2650:
2426:
2420:
2394:
2265:
2099:
Paul
Pritchard, A sublinear additive sieve for finding prime numbers, Communications of the ACM 24 (1981), 18–23.
2686:
2627:
952:
strike off factors of 2 and 3 which are 4 and 6 as factors of 2; 6 as the only factor of 3 is already stricken:
2765:
2589:
2462:
2308:
2260:
1350:
1685:
2604:
2495:
2159:
1571:
which means that it starts at 3 for all odd numbers with the factors of 2 eliminated (circumference of 2),
2715:
2665:
2645:
2129:
Paul
Pritchard, Fast compact prime number sieves (among others), Journal of Algorithms 4 (1983), 332–344.
166:
415:
With a given basis of the first few prime numbers {2, 3, 5}, the "first turn" of the wheel consists of:
216:
Every second thus generated number will be even. Thus odds are generated by the repeated additions of 2:
2366:
2341:
2270:
837:
427:
128:
2725:
2720:
2612:
2594:
2569:
2531:
2275:
1418:
896:
Repeat step 5 until the largest rotation circle spans the largest number to be tested for primality.
35:
2730:
2696:
2617:
2521:
2480:
2475:
2452:
1574:
2561:
2508:
2505:
2346:
2245:
2060:
1535:
1467:
335:
5 = 30, for generating the sequence of 30–coprime numbers by repeated additions of 30; etc.
244:
3 = 6–coprime numbers, will be generated by repeated additions of 6, starting from {1, 5}:
2302:
2295:
2681:
2637:
2351:
2328:
2163:
2050:
339:
Another representation of these wheels is by turning a wheel's numbers, as seen above, into a
157:
Then, for the numbers generated by "rolling the wheel", one needs to only consider the primes
1900:
1622:
2526:
2184:
1989:
1960:
1187:
131:, as none of the generated numbers need be tested in trial divisions by those small primes.
92:
80:
1933:
1870:
1655:
918:
2516:
2415:
2133:
2130:
2118:
2115:
2103:
2100:
1329:{\displaystyle \lim \inf {\frac {\varphi (n)}{n}}\log \log n=e^{-\gamma }\sim 0.56145948,}
151:
2015:
1506:
316:
3 = 6, for generating the sequence of 6–coprime numbers by repeated additions of 6;
226:
Considered by spans of three numbers each, they are enumerated by repeated additions of 2
206:
Considered by spans of two numbers each, they are enumerated by repeated additions of 2:
2546:
2447:
2432:
2336:
2237:
2055:
854:
in a circle. This will be the inner-most circle representing one rotation of the wheel.
803:
124:
2759:
2541:
2226:
2551:
2149:
2065:
807:
799:
143:
138:
With the wheel factorization, one starts from a small list of numbers, called the
2114:
Paul
Pritchard, Explaining the wheel sieve, Acta Informatica 17 (1982), 477–485.
2145:
2195:
84:
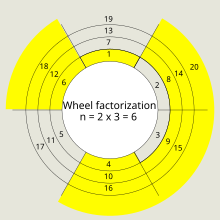
Wheel factorization with n=2x3x5=30. No primes will occur in the yellow areas.
2229:
814:
to generate the remainder of the list. These generators are referred to as
811:
1035:
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
446:
The suggested implementation that follows uses an auxiliary function div(
196:
Natural numbers from 1 and up are enumerated by repeated addition of 1:
293:
1, 7, 11, 13, 17, 19, 23, 29 ; 31, 37, 41, 43, 47, 49, ...
221:
1 ; 3 ; 5 ; 7 ; ...
917:
470:
otherwise. In this implementation, the number to be factorized is
79:
319:{1, 7, 11, 13, 17, 19, 23, 29} (containing eight i.e. (2−1)
283:
1, 5, 7, 11, 13, 17, 19, 23, 25, 29 ; 31, 35, 37, ...
821:
The method may further be applied recursively as a prime number
2199:
249:
1, 5 ; 7, 11 ; 13, 17 ; ...
2083:
Pritchard, Paul, "Linear prime-number sieves: a family tree,"
881:
in concentric circles around the inner-most circle, such that
869:
to be the number of circles written so far, continue to write
18:
16:
Algorithm for generating numbers coprime with first few primes
843:
Multiply the base prime numbers together to give the result
211:
1, 2 ; 3, 4 ; 5, 6 ; ...
798:
Wheel factorization is used for generating lists of mostly
1894:
represents the operation of removing all multiples of x.
2746:
indicate that algorithm is for numbers of special forms
123:
This method can thus be used for an improvement of the
847:
which is the circumference of the factorization wheel.
2018:
1992:
1963:
1936:
1903:
1873:
1688:
1658:
1652:
be the set where k has been added to each element of
1625:
1577:
1538:
1509:
1470:
1421:
1353:
1258:
1190:
258:
sequence can be generated by repeated additions of 2
2674:
2636:
2603:
2560:
2504:
2461:
2365:
2327:
2236:
1174:product. (Note that 1 requires special handling.)
2032:
2004:
1975:
1949:
1922:
1886:
1859:
1671:
1644:
1608:
1563:
1521:
1495:
1449:
1407:
1328:
1202:
474:, and the program returns the smallest divisor of
327:(5−1) numbers) with the "circumference" of 2
312:(3−1) numbers) with the "circumference" of 2
1262:
1259:
235:1, 3, 5 ; 7, 9, 11 ; ...
426:The second turn is obtained by adding 30, the
2211:
1246:, which is also the efficiency of the sieve.
8:
1603:
1591:
1558:
1552:
1490:
1484:
885: + 1 is in the same position as (
2218:
2204:
2196:
173:of all the numbers. This means that fully
146:; then one generates the list, called the
2022:
2017:
1991:
1962:
1941:
1935:
1908:
1902:
1878:
1872:
1833:
1814:
1780:
1761:
1748:
1727:
1722:
1701:
1693:
1687:
1663:
1657:
1630:
1624:
1582:
1576:
1543:
1537:
1508:
1475:
1469:
1429:
1420:
1408:{\displaystyle n=p_{1}p_{2}...p_{i}<x}
1393:
1374:
1364:
1352:
1308:
1265:
1257:
1189:
301:The above showcases first three wheels:
68:Learn how and when to remove this message
2190:Improved incremental prime number sieves
2155:An Introduction to the Theory of Numbers
1860:{\displaystyle S_{np_{i+1}}=F_{p_{i+1}}}
936:Find the first 2 prime numbers: 2 and 3.
2076:
308:{1, 5} (containing two i.e. (2−1)
274:numbers each, into one joined span of
987:Write 7 to 12 with 7 aligned with 1.
154:with all the numbers in the basis.
7:
1169:Analysis and computer implementation
671:factors := add(5, factors)
651:factors := add(3, factors)
631:factors := add(2, factors)
95:with these primes, by construction.
14:
2427:Special number field sieve (SNFS)
2421:General number field sieve (GNFS)
1986:All sets where the circumference
443:remain the same after each turn.
181:; and with basis {2, 3, 5, 7} to
298:This is naturally generalized.
165:When used in finding primes, or
23:
1025:Repeat for the next few lines.
1854:
1851:
1826:
1741:
1450:{\displaystyle np_{i+1}\geq x}
1277:
1271:
1157:
1085:
1040:
1026:
988:
953:
947:
1:
1609:{\displaystyle S_{6}=\{1,5\}}
420:7, 11, 13, 17, 19, 23, 29, 31
2385:Lenstra elliptic curve (ECM)
1930:will be the two smallest of
1564:{\displaystyle S_{2}=\{1\}}
1496:{\displaystyle S_{1}=\{1\}}
1010:+ 1 = 2 ⋅ 6 + 1 = 13.
150:, of the integers that are
43:. The specific problem is:
2782:
2692:Exponentiation by squaring
2375:Continued fraction (CFRAC)
974:+ 1 = 1 ⋅ 6 + 1 = 7.
830:Sample graphical procedure
142:— generally the first few
39:to meet Knowledge (XXG)'s
2739:
1158:2 3 5 7 11 13 17 19 23 29
922:Wheel factorization with
2085:Sci. Comput. Programming
899:Strike off the number 1.
107:(usually no larger than
2605:Greatest common divisor
2160:Oxford University Press
2012:are symmetrical around
1923:{\displaystyle p_{i+1}}
1645:{\displaystyle S_{n}+k}
1503:, which is the set for
1178:last used base primes.
850:Write the numbers 1 to
482:itself if it is prime.
458:is evenly divisible by
454:), which tests whether
2716:Modular exponentiation
2034:
2006:
2005:{\displaystyle n>2}
1977:
1976:{\displaystyle n>2}
1951:
1924:
1888:
1861:
1673:
1646:
1610:
1565:
1523:
1497:
1451:
1409:
1330:
1204:
1203:{\displaystyle k>n}
931:
857:From the numbers 1 to
270:consecutive spans, of
85:
2443:Shanks's square forms
2367:Integer factorization
2342:Sieve of Eratosthenes
2090::1 (1987), pp. 17–35.
2035:
2007:
1978:
1952:
1950:{\displaystyle S_{n}}
1925:
1889:
1887:{\displaystyle F_{x}}
1862:
1674:
1672:{\displaystyle S_{n}}
1647:
1611:
1566:
1524:
1498:
1452:
1410:
1331:
1205:
921:
889: − 1)
838:Sieve of Eratosthenes
266:5 = 30, turning each
129:integer factorization
83:
2721:Montgomery reduction
2595:Function field sieve
2570:Baby-step giant-step
2416:Quadratic sieve (QS)
2016:
1990:
1961:
1934:
1901:
1871:
1686:
1656:
1623:
1575:
1536:
1507:
1468:
1419:
1351:
1256:
1188:
794:Another presentation
103:For a chosen number
50:improve this article
2731:Trachtenberg system
2697:Integer square root
2638:Modular square root
2357:Wheel factorization
2309:Quadratic Frobenius
2289:Lucas–Lehmer–Riesel
2185:Wheel Factorization
2033:{\displaystyle n/2}
1532:Following sets are
1522:{\displaystyle n=1}
1020:= (2 + 1) · 6 = 18.
984:= (1 + 1) · 6 = 12.
724:, factors)
350:"rolling the wheel"
89:Wheel factorization
2623:Extended Euclidean
2562:Discrete logarithm
2491:Schönhage–Strassen
2347:Sieve of Pritchard
2158:(Fifth ed.),
2061:Sieve of Pritchard
2030:
2002:
1973:
1947:
1920:
1884:
1857:
1669:
1642:
1606:
1561:
1519:
1493:
1447:
1405:
1326:
1200:
932:
873: + 1 to
201:1, 2, 3, 4, 5, ...
86:
2753:
2752:
2352:Sieve of Sundaram
2192:by Paul Pritchard
2169:978-0-19-853171-5
2051:Sieve of Sundaram
1284:
1249:It is known that
619:factors :=
411:A typical example
78:
77:
70:
41:quality standards
32:This article may
2773:
2702:Integer relation
2675:Other algorithms
2580:Pollard kangaroo
2471:Ancient Egyptian
2329:Prime-generating
2314:Solovay–Strassen
2227:Number-theoretic
2220:
2213:
2206:
2197:
2173:
2172:
2142:
2136:
2127:
2121:
2112:
2106:
2097:
2091:
2081:
2039:
2037:
2036:
2031:
2026:
2011:
2009:
2008:
2003:
1982:
1980:
1979:
1974:
1956:
1954:
1953:
1948:
1946:
1945:
1929:
1927:
1926:
1921:
1919:
1918:
1893:
1891:
1890:
1885:
1883:
1882:
1866:
1864:
1863:
1858:
1844:
1843:
1819:
1818:
1785:
1784:
1766:
1765:
1753:
1752:
1740:
1739:
1738:
1737:
1714:
1713:
1712:
1711:
1678:
1676:
1675:
1670:
1668:
1667:
1651:
1649:
1648:
1643:
1635:
1634:
1615:
1613:
1612:
1607:
1587:
1586:
1570:
1568:
1567:
1562:
1548:
1547:
1528:
1526:
1525:
1520:
1502:
1500:
1499:
1494:
1480:
1479:
1456:
1454:
1453:
1448:
1440:
1439:
1414:
1412:
1411:
1406:
1398:
1397:
1379:
1378:
1369:
1368:
1345:Euler's constant
1342:
1335:
1333:
1332:
1327:
1316:
1315:
1285:
1280:
1266:
1245:
1216:is not prime if
1211:
1209:
1207:
1206:
1201:
1021:
997:7 8 9 10 11 12
985:
948:1 2 3 4 5 6
944:
929:
439:
421:
334:
330:
326:
322:
315:
311:
294:
284:
265:
261:
250:
243:
236:
229:
222:
212:
202:
184:
180:
176:
172:
73:
66:
62:
59:
53:
27:
26:
19:
2781:
2780:
2776:
2775:
2774:
2772:
2771:
2770:
2766:Primality tests
2756:
2755:
2754:
2749:
2735:
2670:
2632:
2599:
2556:
2500:
2457:
2361:
2323:
2296:Proth's theorem
2238:Primality tests
2232:
2224:
2181:
2176:
2170:
2144:
2143:
2139:
2128:
2124:
2113:
2109:
2098:
2094:
2082:
2078:
2074:
2047:
2014:
2013:
1988:
1987:
1959:
1958:
1937:
1932:
1931:
1904:
1899:
1898:
1874:
1869:
1868:
1829:
1810:
1776:
1757:
1744:
1723:
1718:
1697:
1689:
1684:
1683:
1659:
1654:
1653:
1626:
1621:
1620:
1578:
1573:
1572:
1539:
1534:
1533:
1505:
1504:
1471:
1466:
1465:
1425:
1417:
1416:
1389:
1370:
1360:
1349:
1348:
1340:
1304:
1267:
1254:
1253:
1230:
1212:, we know that
1186:
1185:
1183:
1171:
1162:
1159:
1153:
1081:
1036:
1024:
1023:Write 13 to 18.
1022:
1011:
1006:
1001:
998:
986:
975:
970:
965:
962:
949:
939:
927:
916:
893: + 1.
832:
796:
791:
613:
437:
419:
413:
332:
328:
324:
320:
313:
309:
292:
282:
263:
259:
248:
241:
234:
227:
220:
210:
200:
194:
183:48/210 < 23%
182:
178:
174:
170:
101:
74:
63:
57:
54:
47:
28:
24:
17:
12:
11:
5:
2779:
2777:
2769:
2768:
2758:
2757:
2751:
2750:
2748:
2747:
2740:
2737:
2736:
2734:
2733:
2728:
2723:
2718:
2713:
2699:
2694:
2689:
2684:
2678:
2676:
2672:
2671:
2669:
2668:
2663:
2658:
2656:Tonelli–Shanks
2653:
2648:
2642:
2640:
2634:
2633:
2631:
2630:
2625:
2620:
2615:
2609:
2607:
2601:
2600:
2598:
2597:
2592:
2590:Index calculus
2587:
2585:Pohlig–Hellman
2582:
2577:
2572:
2566:
2564:
2558:
2557:
2555:
2554:
2549:
2544:
2539:
2537:Newton-Raphson
2534:
2529:
2524:
2519:
2513:
2511:
2502:
2501:
2499:
2498:
2493:
2488:
2483:
2478:
2473:
2467:
2465:
2463:Multiplication
2459:
2458:
2456:
2455:
2450:
2448:Trial division
2445:
2440:
2435:
2433:Rational sieve
2430:
2423:
2418:
2413:
2405:
2397:
2392:
2387:
2382:
2377:
2371:
2369:
2363:
2362:
2360:
2359:
2354:
2349:
2344:
2339:
2337:Sieve of Atkin
2333:
2331:
2325:
2324:
2322:
2321:
2316:
2311:
2306:
2299:
2292:
2285:
2278:
2273:
2268:
2263:
2261:Elliptic curve
2258:
2253:
2248:
2242:
2240:
2234:
2233:
2225:
2223:
2222:
2215:
2208:
2200:
2194:
2193:
2187:
2180:
2179:External links
2177:
2175:
2174:
2168:
2137:
2122:
2107:
2092:
2075:
2073:
2070:
2069:
2068:
2063:
2058:
2056:Sieve of Atkin
2053:
2046:
2043:
2042:
2041:
2029:
2025:
2021:
2001:
1998:
1995:
1984:
1972:
1969:
1966:
1944:
1940:
1917:
1914:
1911:
1907:
1895:
1881:
1877:
1856:
1853:
1850:
1847:
1842:
1839:
1836:
1832:
1828:
1825:
1822:
1817:
1813:
1809:
1806:
1803:
1800:
1797:
1794:
1791:
1788:
1783:
1779:
1775:
1772:
1769:
1764:
1760:
1756:
1751:
1747:
1743:
1736:
1733:
1730:
1726:
1721:
1717:
1710:
1707:
1704:
1700:
1696:
1692:
1680:
1666:
1662:
1641:
1638:
1633:
1629:
1617:
1605:
1602:
1599:
1596:
1593:
1590:
1585:
1581:
1560:
1557:
1554:
1551:
1546:
1542:
1530:
1518:
1515:
1512:
1492:
1489:
1486:
1483:
1478:
1474:
1446:
1443:
1438:
1435:
1432:
1428:
1424:
1404:
1401:
1396:
1392:
1388:
1385:
1382:
1377:
1373:
1367:
1363:
1359:
1356:
1337:
1336:
1325:
1322:
1319:
1314:
1311:
1307:
1303:
1300:
1297:
1294:
1291:
1288:
1283:
1279:
1276:
1273:
1270:
1264:
1261:
1199:
1196:
1193:
1170:
1167:
1161:
1160:
1154:
1082:
1037:
999:
963:
950:
945:
937:
933:
915:
912:
911:
910:
906:
903:
900:
897:
894:
863:
855:
848:
841:
831:
828:
804:trial division
795:
792:
746:+ inc
618:
484:
466:in this case,
462:, and returns
441:
440:
424:
423:
412:
409:
408:
407:
337:
336:
317:
306:
296:
295:
286:
285:
252:
251:
238:
237:
224:
223:
214:
213:
204:
203:
193:
190:
125:trial division
100:
97:
76:
75:
31:
29:
22:
15:
13:
10:
9:
6:
4:
3:
2:
2778:
2767:
2764:
2763:
2761:
2745:
2742:
2741:
2738:
2732:
2729:
2727:
2724:
2722:
2719:
2717:
2714:
2711:
2707:
2703:
2700:
2698:
2695:
2693:
2690:
2688:
2685:
2683:
2680:
2679:
2677:
2673:
2667:
2664:
2662:
2659:
2657:
2654:
2652:
2651:Pocklington's
2649:
2647:
2644:
2643:
2641:
2639:
2635:
2629:
2626:
2624:
2621:
2619:
2616:
2614:
2611:
2610:
2608:
2606:
2602:
2596:
2593:
2591:
2588:
2586:
2583:
2581:
2578:
2576:
2573:
2571:
2568:
2567:
2565:
2563:
2559:
2553:
2550:
2548:
2545:
2543:
2540:
2538:
2535:
2533:
2530:
2528:
2525:
2523:
2520:
2518:
2515:
2514:
2512:
2510:
2507:
2503:
2497:
2494:
2492:
2489:
2487:
2484:
2482:
2479:
2477:
2474:
2472:
2469:
2468:
2466:
2464:
2460:
2454:
2451:
2449:
2446:
2444:
2441:
2439:
2436:
2434:
2431:
2429:
2428:
2424:
2422:
2419:
2417:
2414:
2412:
2410:
2406:
2404:
2402:
2398:
2396:
2395:Pollard's rho
2393:
2391:
2388:
2386:
2383:
2381:
2378:
2376:
2373:
2372:
2370:
2368:
2364:
2358:
2355:
2353:
2350:
2348:
2345:
2343:
2340:
2338:
2335:
2334:
2332:
2330:
2326:
2320:
2317:
2315:
2312:
2310:
2307:
2305:
2304:
2300:
2298:
2297:
2293:
2291:
2290:
2286:
2284:
2283:
2279:
2277:
2274:
2272:
2269:
2267:
2264:
2262:
2259:
2257:
2254:
2252:
2249:
2247:
2244:
2243:
2241:
2239:
2235:
2231:
2228:
2221:
2216:
2214:
2209:
2207:
2202:
2201:
2198:
2191:
2188:
2186:
2183:
2182:
2178:
2171:
2165:
2161:
2157:
2156:
2151:
2150:Wright, E. M.
2147:
2141:
2138:
2135:
2132:
2126:
2123:
2120:
2117:
2111:
2108:
2105:
2102:
2096:
2093:
2089:
2086:
2080:
2077:
2071:
2067:
2064:
2062:
2059:
2057:
2054:
2052:
2049:
2048:
2044:
2027:
2023:
2019:
1999:
1996:
1993:
1985:
1970:
1967:
1964:
1942:
1938:
1915:
1912:
1909:
1905:
1896:
1879:
1875:
1848:
1845:
1840:
1837:
1834:
1830:
1823:
1820:
1815:
1811:
1807:
1804:
1801:
1798:
1795:
1792:
1789:
1786:
1781:
1777:
1773:
1770:
1767:
1762:
1758:
1754:
1749:
1745:
1734:
1731:
1728:
1724:
1719:
1715:
1708:
1705:
1702:
1698:
1694:
1690:
1681:
1664:
1660:
1639:
1636:
1631:
1627:
1618:
1600:
1597:
1594:
1588:
1583:
1579:
1555:
1549:
1544:
1540:
1531:
1516:
1513:
1510:
1487:
1481:
1476:
1472:
1463:
1462:
1461:
1458:
1444:
1441:
1436:
1433:
1430:
1426:
1422:
1402:
1399:
1394:
1390:
1386:
1383:
1380:
1375:
1371:
1365:
1361:
1357:
1354:
1346:
1323:
1320:
1317:
1312:
1309:
1305:
1301:
1298:
1295:
1292:
1289:
1286:
1281:
1274:
1268:
1252:
1251:
1250:
1247:
1244:
1240:
1236:
1235:
1227:
1223:
1219:
1215:
1197:
1194:
1191:
1179:
1175:
1168:
1166:
1155:
1152:
1148:
1145:
1142:
1138:
1134:
1131:
1128:
1124:
1120:
1117:
1114:
1110:
1106:
1103:
1100:
1096:
1092:
1088:
1083:
1079:
1076:
1073:22 23 24 25
1072:
1069:
1066:16 17 18 19
1065:
1062:
1059:10 11 12 13
1058:
1055:
1051:
1047:
1043:
1038:
1034:
1030:
1019:
1015:
1009:
1004:
1000:
996:
992:
983:
979:
973:
968:
964:
961:
957:
951:
946:
942:
938:
935:
934:
925:
920:
913:
907:
904:
901:
898:
895:
892:
888:
884:
880:
877: +
876:
872:
868:
864:
860:
856:
853:
849:
846:
842:
839:
834:
833:
829:
827:
824:
819:
817:
813:
809:
805:
801:
800:prime numbers
793:
789:
785:
781:
777:
774:
770:
767:
763:
759:
756:
752:
749:
745:
741:
738:
735:
731:
727:
723:
719:
715:
711:
707:
704:
701:
697:
693:
690:
686:
682:
678:
674:
670:
666:
662:
658:
654:
650:
646:
642:
638:
634:
630:
626:
622:
617:
612:
609:
605:
602:
598:
594:
591:
587:
584:
580:
576:
573:
569:
565:
561:
557:
554:
551:
547:
543:
540:
536:
532:
528:
525:
521:
517:
513:
510:
506:
502:
498:
495:
491:
487:
483:
481:
477:
473:
469:
465:
461:
457:
453:
449:
444:
436:
435:
434:
431:
429:
418:
417:
416:
410:
405:
401:
397:
393:
389:
385:
381:
377:
373:
369:
365:
361:
358:
357:
356:
353:
351:
346:
342:
341:circular list
318:
307:
304:
303:
302:
299:
291:
290:
289:
281:
280:
279:
277:
273:
269:
257:
247:
246:
245:
233:
232:
231:
219:
218:
217:
209:
208:
207:
199:
198:
197:
191:
189:
186:
179:8/30 < 27%
168:
163:
160:
155:
153:
149:
145:
144:prime numbers
141:
136:
132:
130:
126:
121:
118:
115:), the first
114:
110:
106:
98:
96:
94:
90:
82:
72:
69:
61:
58:February 2015
51:
46:
42:
38:
37:
30:
21:
20:
2743:
2425:
2408:
2400:
2356:
2319:Miller–Rabin
2301:
2294:
2287:
2282:Lucas–Lehmer
2280:
2162:, thm. 328,
2153:
2146:Hardy, G. H.
2140:
2125:
2110:
2095:
2087:
2084:
2079:
2066:Sieve theory
1459:
1338:
1248:
1242:
1238:
1233:
1225:
1221:
1217:
1213:
1180:
1176:
1172:
1163:
1150:
1146:
1143:
1140:
1136:
1132:
1129:
1126:
1122:
1118:
1115:
1112:
1108:
1104:
1101:
1098:
1094:
1090:
1086:
1077:
1074:
1070:
1067:
1063:
1060:
1056:
1053:
1049:
1045:
1041:
1032:
1028:
1017:
1013:
1007:
1002:
994:
990:
981:
977:
971:
966:
959:
955:
940:
923:
890:
886:
882:
878:
874:
870:
866:
858:
851:
844:
822:
820:
815:
797:
787:
783:
779:
775:
772:
768:
765:
761:
757:
754:
750:
747:
743:
739:
736:
733:
729:
725:
721:
717:
713:
709:
705:
702:
699:
695:
691:
688:
684:
683: := 7;
680:
676:
672:
668:
667:, 5) = true
664:
660:
656:
652:
648:
647:, 3) = true
644:
640:
636:
632:
628:
627:, 2) = true
624:
620:
614:
610:
607:
603:
600:
596:
592:
589:
585:
582:
578:
574:
571:
567:
563:
559:
555:
552:
549:
545:
541:
538:
534:
533: := 7;
530:
526:
523:
522:, 5) = true
519:
515:
511:
508:
507:, 3) = true
504:
500:
496:
493:
492:, 2) = true
489:
485:
479:
478:– returning
475:
471:
467:
463:
459:
455:
451:
447:
445:
442:
432:
425:
414:
403:
399:
395:
391:
387:
383:
379:
375:
371:
367:
363:
359:
354:
349:
344:
340:
338:
300:
297:
287:
275:
271:
267:
255:
253:
239:
225:
215:
205:
195:
192:Introduction
187:
171:1/3 < 34%
164:
158:
156:
147:
139:
137:
133:
122:
116:
112:
108:
104:
102:
88:
87:
64:
55:
48:Please help
44:
33:
2575:Pollard rho
2532:Goldschmidt
2266:Pocklington
2256:Baillie–PSW
1464:Start with
943:= 2 × 3 = 6
909:non-primes.
823:wheel sieve
786:, factors)
771: := 0
687: := 0
606: := 0
537: := 0
406:+2=43; etc.
345:differences
323:(3−1)
127:method for
99:Description
52:if you can.
2687:Cornacchia
2682:Chakravala
2230:algorithms
2072:References
1321:0.56145948
1231:1 −
581:+ inc
566:) = true,
352:metaphor.
2661:Berlekamp
2618:Euclidean
2506:Euclidean
2486:Toom–Cook
2481:Karatsuba
1846:−
1808:∪
1796:∪
1774:∪
1755:∪
1442:≥
1318:∼
1313:γ
1310:−
1296:
1290:
1269:φ
1027:1 2 3
989:1 2 3
954:1 2 3
812:algorithm
760: :=
742: :=
728: :=
716:) = true
675: :=
655: :=
635: :=
595: :=
577: :=
278:numbers:
2760:Category
2628:Lehmer's
2522:Chunking
2509:division
2438:Fermat's
2152:(1979),
2045:See also
1084:Sieving
1080:28 29 30
1039:Sieving
790:factors
34:require
2744:Italics
2666:Kunerth
2646:Cipolla
2527:Fourier
2496:Fürer's
2390:Euler's
2380:Dixon's
2303:Pépin's
1210:
1184:
914:Example
865:Taking
862:wheels.
778:> 1
753:< 7
588:< 7
570:return
438:inc = ,
428:product
402:+4=41;
398:+6=37;
394:+2=31;
390:+6=29;
386:+4=23;
382:+2=19;
378:+4=17;
374:+2=13;
370:+4=11;
343:of the
230:3 = 6:
167:sieving
152:coprime
93:coprime
36:cleanup
2726:Schoof
2613:Binary
2517:Binary
2453:Shor's
2271:Fermat
2166:
2134:729229
2119:685983
2104:600730
1897:1 and
1867:where
1341:γ
1339:where
1234:φ
1089:2 3
1044:2 3
816:wheels
808:sieves
788:return
616:list.
608:return
527:return
512:return
497:return
366:+6=7;
2547:Short
2276:Lucas
1957:when
1682:Then
689:while
661:while
641:while
621:while
539:while
468:false
148:wheel
140:basis
2542:Long
2476:Long
2164:ISBN
1997:>
1968:>
1619:Let
1415:and
1400:<
1241:) /
1224:and
1220:mod
1195:>
1016:+ 1)
1005:= 2.
980:+ 1)
969:= 1.
782:add(
780:then
766:else
764:+ 1
755:then
737:else
720:add(
718:then
708:div(
679:/ 5
663:div(
659:/ 3
643:div(
639:/ 2
623:div(
601:else
599:+ 1
590:then
568:then
558:div(
524:then
518:div(
509:then
503:div(
494:then
488:div(
464:true
362:=1;
268:five
256:same
254:The
2706:LLL
2552:SRT
2411:+ 1
2403:− 1
2251:APR
2246:AKS
1343:is
1293:log
1287:log
1263:inf
1260:lim
1149:29
1139:25
1135:23
1125:19
1121:17
1111:13
1107:11
1097:7
1093:5
1052:7
1048:5
1031:5
993:5
958:5
930:3=6
806:or
276:ten
272:two
185:.
175:2/3
159:not
111:or
2762::
2710:KZ
2708:;
2148:;
2131:MR
2116:MR
2101:MR
1151:30
1147:28
1144:27
1141:26
1137:24
1133:22
1130:21
1127:20
1123:18
1119:16
1116:15
1113:14
1109:12
1105:10
1078:27
1075:26
1071:21
1068:20
1064:15
1061:14
1008:xn
972:xn
928:×
926:=2
883:xn
875:xn
871:xn
773:if
748:if
732:/
712:,
706:if
703:do
698:≤
694:*
669:do
649:do
629:do
583:if
562:,
556:if
553:do
548:≤
544:*
529:5
516:if
514:3
501:if
499:2
486:if
450:,
333:×
329:×
325:×
321:×
314:×
310:×
264:×
260:×
242:×
228:×
2712:)
2704:(
2409:p
2401:p
2219:e
2212:t
2205:v
2088:9
2028:2
2024:/
2020:n
2000:2
1994:n
1971:2
1965:n
1943:n
1939:S
1916:1
1913:+
1910:i
1906:p
1880:x
1876:F
1855:]
1852:)
1849:1
1841:1
1838:+
1835:i
1831:p
1827:(
1824:n
1821:+
1816:n
1812:S
1805:.
1802:.
1799:.
1793:n
1790:2
1787:+
1782:n
1778:S
1771:n
1768:+
1763:n
1759:S
1750:n
1746:S
1742:[
1735:1
1732:+
1729:i
1725:p
1720:F
1716:=
1709:1
1706:+
1703:i
1699:p
1695:n
1691:S
1679:.
1665:n
1661:S
1640:k
1637:+
1632:n
1628:S
1604:}
1601:5
1598:,
1595:1
1592:{
1589:=
1584:6
1580:S
1559:}
1556:1
1553:{
1550:=
1545:2
1541:S
1517:1
1514:=
1511:n
1491:}
1488:1
1485:{
1482:=
1477:1
1473:S
1445:x
1437:1
1434:+
1431:i
1427:p
1423:n
1403:x
1395:i
1391:p
1387:.
1384:.
1381:.
1376:2
1372:p
1366:1
1362:p
1358:=
1355:n
1324:,
1306:e
1302:=
1299:n
1282:n
1278:)
1275:n
1272:(
1243:n
1239:n
1237:(
1226:n
1222:n
1218:k
1214:k
1198:n
1192:k
1102:9
1099:8
1095:6
1091:4
1087:1
1057:9
1054:8
1050:6
1046:4
1042:1
1033:6
1029:4
1018:n
1014:x
1012:(
1003:x
995:6
991:4
982:n
978:x
976:(
967:x
960:6
956:4
941:n
924:n
891:n
887:x
879:n
867:x
859:n
852:n
845:n
840:.
784:n
776:n
769:i
762:i
758:i
751:i
744:k
740:k
734:k
730:n
726:n
722:k
714:k
710:n
700:n
696:k
692:k
685:i
681:k
677:n
673:n
665:n
657:n
653:n
645:n
637:n
633:n
625:n
611:n
604:i
597:i
593:i
586:i
579:k
575:k
572:k
564:k
560:n
550:n
546:k
542:k
535:i
531:k
520:n
505:n
490:n
480:n
476:n
472:n
460:k
456:n
452:k
448:n
422:.
404:n
400:n
396:n
392:n
388:n
384:n
380:n
376:n
372:n
368:n
364:n
360:n
331:3
262:3
117:n
113:5
109:4
105:n
71:)
65:(
60:)
56:(
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.