79:
giving a universal space of parameters for the problem. For example, consider the problem of finding all circles in the
Euclidean plane up to congruence. Any circle can be described uniquely by giving three points, but many different sets of three points give the same circle: the correspondence is many-to-one. However, circles are uniquely parameterized by giving their center and radius: this is two real parameters and one positive real parameter. Since we are only interested in circles "up to congruence", we identify circles having different centers but the same radius, and so the radius alone suffices to parameterize the set of interest. The moduli space is, therefore, the
96:
2490:. Both moduli stacks carry universal families of curves. One can also define coarse moduli spaces representing isomorphism classes of smooth or stable curves. These coarse moduli spaces were actually studied before the notion of moduli stack was invented. In fact, the idea of a moduli stack was invented by Deligne and Mumford in an attempt to prove the projectivity of the coarse moduli spaces. In recent years, it has become apparent that the stack of curves is actually the more fundamental object.
1285:
1083:
62:) can be given the structure of a geometric space, then one can parametrize such objects by introducing coordinates on the resulting space. In this context, the term "modulus" is used synonymously with "parameter"; moduli spaces were first understood as spaces of parameters rather than as spaces of objects. A variant of moduli spaces is
2902:
More precisely, the existence of non-trivial automorphisms of the objects being classified makes it impossible to have a fine moduli space. However, it is often possible to consider a modified moduli problem of classifying the original objects together with additional data, chosen in such a way that
2349:
should not be constant, but would have to be constant on any proper open set by triviality), one can still sometimes obtain a coarse moduli space. However, this approach is not ideal, as such spaces are not guaranteed to exist, they are frequently singular when they do exist, and miss details about
78:
Moduli spaces are spaces of solutions of geometric classification problems. That is, the points of a moduli space correspond to solutions of geometric problems. Here different solutions are identified if they are isomorphic (that is, geometrically the same). Moduli spaces can be thought of as
3020:
of this latter ring can then be viewed as giving a kind of coordinate chart on the desired moduli space. By gluing together enough of these charts, we can cover the space, but the map from our union of spectra to the moduli space will, in general, be many to one. We, therefore, define an
2281:
is a space which has a point for every object that could appear in a family, and whose geometry reflects the ways objects can vary in families. Note, however, that a coarse moduli space does not necessarily carry any family of appropriate objects, let alone a universal one.
1280:{\displaystyle \mathbf {P} _{\mathbb {Z} }^{n}(X)=\left\{({\mathcal {L}},s_{0},\ldots ,s_{n}):{\begin{matrix}{\mathcal {L}}\to X{\text{ is a line bundle}}\\s_{0},\ldots ,s_{n}\in \Gamma (X,{\mathcal {L}})\\{\text{ form a basis of global sections}}\end{matrix}}\right\}/\sim }
2505:> 1. In lower genus, one must account for the presence of smooth families of automorphisms, by subtracting their number. There is exactly one complex curve of genus zero, the Riemann sphere, and its group of isomorphisms is PGL(2). Hence, the dimension of
897:
91:
for determining when two circles are "close". The geometric structure of moduli spaces locally tells us when two solutions of a geometric classification problem are "close", but generally moduli spaces also have a complicated global structure as well.
2750:
In higher dimensions, moduli of algebraic varieties are more difficult to construct and study. For instance, the higher-dimensional analogue of the moduli space of elliptic curves discussed above is the moduli space of abelian varieties, such as the
2454:> 1, this stack may be compactified by adding new "boundary" points which correspond to stable nodal curves (together with their isomorphisms). A curve is stable if it has only a finite group of automorphisms. The resulting stack is denoted
2583:> 1 because the curves with genus g > 1 have only a finite group as its automorphism i.e. dim(a group of automorphisms) = 0. Eventually, in genus zero, the coarse moduli space has dimension zero, and in genus one, it has dimension one.
1803:
86:
Moduli spaces often carry natural geometric and topological structures as well. In the example of circles, for instance, the moduli space is not just an abstract set, but the absolute value of the difference of the radii defines a
607:
1052:
1900:
1402:
487:
758:
945:
2970:. Consequently, the moduli space of smooth curves and linear systems (satisfying certain criteria) may be embedded in the Hilbert scheme of a sufficiently high-dimensional projective space. This locus
2203:
Fine moduli spaces are desirable, but they do not always exist and are frequently difficult to construct, so mathematicians sometimes use a weaker notion, the idea of a coarse moduli space. A space
1336:
2732:
2679:
2594:
marked points. Such marked curves are said to be stable if the subgroup of curve automorphisms which fix the marked points is finite. The resulting moduli stacks of smooth (or stable) genus
360:
2488:
1468:
2903:
the identity is the only automorphism respecting also the additional data. With a suitable choice of the rigidifying data, the modified moduli problem will have a (fine) moduli space
997:
533:
3553:
Papadopoulos, Athanase, ed. (2012), Handbook of Teichmüller theory. Vol. III, IRMA Lectures in
Mathematics and Theoretical Physics, 17, European Mathematical Society (EMS), Zürich,
2844:, which like the moduli space of curves, was studied before stacks were invented. When the bundles have rank 1 and degree zero, the study of coarse moduli space is the study of the
3528:
Papadopoulos, Athanase, ed. (2009), Handbook of Teichmüller theory. Vol. II, IRMA Lectures in
Mathematics and Theoretical Physics, 13, European Mathematical Society (EMS), Zürich,
3503:
Papadopoulos, Athanase, ed. (2007), Handbook of Teichmüller theory. Vol. I, IRMA Lectures in
Mathematics and Theoretical Physics, 11, European Mathematical Society (EMS), Zürich,
2637:
1498:
390:
2573:
2534:
2444:
2392:
of a given genus. The language of algebraic stacks essentially provides a systematic way to view the fibred category that constitutes the moduli problem as a "space", and the
1703:
3025:
on the former; essentially, two points are equivalent if the objects over each are isomorphic. This gives a scheme and an equivalence relation, which is enough to define an
1982:
There are several related notions of things we could call moduli spaces. Each of these definitions formalizes a different notion of what it means for the points of space
769:
4149:
3343:
1711:
3359:. Third edition. Ergebnisse der Mathematik und ihrer Grenzgebiete (2) (Results in Mathematics and Related Areas (2)), 34. Springer-Verlag, Berlin, 1994. xiv+292 pp.
54:
of such objects. Such spaces frequently arise as solutions to classification problems: If one can show that a collection of interesting objects (e.g., the smooth
1932:
3751:
1524:
416:
2891:), and spaces (almost) representing them, dates back to Grothendieck (1960/61), in which he described the general framework, approaches, and main problems using
1972:
1952:
1674:
1075:
324:
2923:, and the problem of constructing the moduli space becomes that of finding a scheme (or more general space) that is (in a suitably strong sense) the quotient
2544:
Likewise, in genus 1, there is a one-dimensional space of curves, but every such curve has a one-dimensional group of automorphisms. Hence, the stack
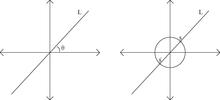
232:, we capture the ways in which the members (lines in this case) of the family can modulate by continuously varying 0 ≤ θ < π.
544:
2388:
Algebraic stacks and their use to analyze moduli problems appeared in
Deligne-Mumford (1969) as a tool to prove the irreducibility of the (coarse)
1005:
1814:
1656:, and every closed subscheme is represented by such a point. A simple example of a Hilbert scheme is the Hilbert scheme parameterizing degree
1341:
3720:
3641:
3604:
3566:
3541:
3516:
3479:
3444:
3292:
2895:
in complex analytical geometry as an example. The talks, in particular, describe the general method of constructing moduli spaces by first
2796:
The construction of moduli spaces of Calabi-Yau varieties is an important open problem, and only special cases such as moduli spaces of
3744:
2978:) which mixes the elements of the linear system; consequently, the moduli space of smooth curves is then recovered as the quotient of
421:
4116:
3370:
618:
2777:
Using techniques arising out of differential geometry and birational geometry simultaneously, the construction of moduli spaces of
3013:
2883:
The modern formulation of moduli problems and definition of moduli spaces in terms of the moduli functors (or more generally the
4346:
4081:
3320:"Techniques de construction en géométrie analytique. I. Description axiomatique de l'espace de Teichmüller et de ses variantes"
3130:
3431:. Ergebnisse der Mathematik und ihrer Grenzgebiete. Vol. 22. With an appendix by David Mumford. Berlin: Springer-Verlag.
4708:
3009:
905:
2377:
to describe a moduli problem goes back to
Grothendieck (1960/61). In general, they cannot be represented by schemes or even
1293:
3684:
2872:
2353:
A more sophisticated approach is to enrich the classification by remembering the isomorphisms. More precisely, on any base
4288:
3794:
3737:
3135:
2782:
2766:
Using techniques arising out of the minimal model program, moduli spaces of varieties of general type were constructed by
4058:
2915:. The rigidifying data is moreover chosen so that it corresponds to a principal bundle with an algebraic structure group
123:
of this family a quantity that can uniquely identify it—a modulus. An example of such a quantity is the positive angle θ(
4733:
3789:
3012:
provides an object of the desired kind over a base which is a complete local ring. This object can be approximated via
1577:
4313:
3226:
2695:
2642:
3939:
329:
2457:
4234:
3886:
3580:
3471:
3125:
2940:
2410:
2389:
2090:
1407:
3160:
4939:
4573:
4528:
95:
4753:
4673:
4488:
4422:
3784:
3687:
3067:
3052:
2771:
257:
4633:
4255:
4229:
3970:
2812:
Another important moduli problem is to understand the geometry of (various substacks of) the moduli stack Vect
3155:
2317:. This in particular makes the existence of a fine moduli space impossible (intuitively, the idea is that if
495:
4893:
4703:
4417:
4260:
4101:
3859:
3801:
203:
2939:. The last problem, in general, does not admit a solution; however, it is addressed by the groundbreaking
4934:
4658:
4399:
4205:
4096:
4068:
3891:
3402:
3315:
3006:
2955:
2752:
2605:
4808:
4144:
4111:
3975:
3817:
2919:. Thus one can move back from the rigidified problem to the original by taking quotient by the action of
1473:
950:
365:
4513:
4453:
4394:
4361:
4356:
4154:
3852:
3847:
3842:
3827:
3071:
2547:
2508:
2418:
2140:
246:
80:
4683:
2396:
of many moduli problems is better-behaved (such as smooth) than the corresponding coarse moduli space.
1679:
1290:
Showing this is true can be done by running through a series of tautologies: any projective embedding
4898:
3896:
3881:
3837:
3112:
3022:
2892:
140:
88:
43:
2855:, the number of moduli of vector bundles and the closely related problem of the number of moduli of
2840:
is one-dimensional, and especially when n equals one. In this case, the coarse moduli space is the
892:{\displaystyle ({\mathcal {L}},(s_{0},\ldots ,s_{n}))\sim ({\mathcal {L}}',(s_{0}',\ldots ,s_{n}'))}
4813:
4698:
4351:
4250:
3876:
3407:
3075:
2756:
2014:
150:
that intersect the origin by means of a topological construction. To wit: consider the unit circle
4858:
4778:
4678:
4638:
4518:
4483:
4318:
4195:
4091:
3832:
3319:
3102:
3017:
2990:
35:
4568:
4245:
2767:
1798:{\displaystyle {\mathcal {Hilb}}_{d}(\mathbb {P} ^{n})=\mathbb {P} (\Gamma ({\mathcal {O}}(d)))}
3297:
3249:
J. Kollar. Moduli of varieties of general type, Handbook of moduli. Vol. II, 2013, pp. 131–157.
4823:
4728:
4563:
4473:
4443:
4239:
4134:
4086:
3980:
3716:
3680:
3654:
3637:
3600:
3562:
3537:
3512:
3475:
3440:
3387:
3366:
3181:
3060:
2830:
2801:
199:
51:
2950:
To see how this might work, consider the problem of parametrizing smooth curves of the genus
2313:
It is frequently the case that interesting geometric objects come equipped with many natural
4833:
4768:
4738:
4618:
4558:
4523:
4468:
4458:
4438:
4371:
4323:
4281:
4186:
4179:
4172:
4165:
4158:
4076:
3866:
3774:
3708:
3669:
3592:
3554:
3529:
3504:
3432:
3412:
3042:
2845:
2074:
67:
59:
3685:"Simple geodesics and Weil-Petersson volumes of moduli spaces of bordered Riemann surfaces"
3614:
3548:
3523:
3489:
3454:
3363:
3350:
3115:, general criterion for constructing moduli spaces as algebraic stacks from moduli functors
2785:
varieties. In this setting important results about boundedness of Fano varieties proven by
4913:
4868:
4818:
4803:
4793:
4688:
4653:
4478:
4048:
3822:
3610:
3588:
3545:
3520:
3485:
3450:
3360:
3347:
3030:
3026:
2884:
2760:
2382:
2378:
2362:
1908:
55:
47:
4758:
1503:
395:
17:
4888:
4883:
4843:
4783:
4773:
4693:
4613:
4603:
4598:
4593:
4508:
4503:
4498:
4463:
4448:
4376:
4053:
3916:
3624:
3383:
3272:
3145:
3092:
2989:. Here the idea is to start with an object of the kind to be classified and study its
2908:
2786:
2778:
2735:
1957:
1937:
1659:
1634:
1060:
309:
2540:
dim(space of genus zero curves) − dim(group of automorphisms) = 0 − dim(PGL(2)) = −3.
2497:−3; hence a stable nodal curve can be completely specified by choosing the values of 3
4928:
4878:
4863:
4838:
4828:
4798:
4743:
4718:
4663:
4648:
4643:
4608:
4583:
4543:
4333:
3985:
3901:
3779:
3760:
3655:"Moduli of representations of the fundamental group of a smooth projective variety I"
3424:
3335:
3140:
3002:
2994:
2986:
2944:
2841:
2826:
63:
4908:
4748:
4628:
4578:
4548:
4533:
4341:
4200:
4126:
4106:
4043:
3906:
3628:
3107:
3056:
2860:
2856:
2790:
2739:
2361:
with only isomorphisms between families taken as morphisms. One then considers the
2314:
268:
27:
Geometric space whose points represent algebro-geometric objects of some fixed kind
302:
Projective space as moduli of very ample line bundles generated by global sections
4903:
4873:
4853:
4713:
4668:
4623:
4588:
4538:
4303:
4272:
4033:
3990:
3700:
3463:
3150:
3097:
2947:
in 1965, which shows that under suitable conditions the quotient indeed exists.
2912:
31:
3712:
4848:
4788:
4723:
4386:
4366:
4265:
4224:
4038:
3436:
2797:
602:{\displaystyle {\hat {x}}:{\text{Spec}}(R)\to \mathbf {P} _{\mathbb {Z} }^{n}}
1047:{\displaystyle \mathbf {P} _{\mathbb {Z} }^{n}:{\text{Sch}}\to {\text{Sets}}}
4763:
4553:
4493:
4139:
4013:
3934:
3929:
3924:
3202:
2966:
is equivalent to a closed one dimensional subscheme of the projective space
1535:
3705:
Proceedings of the
International Congress of Mathematicians 2010 (ICM 2010)
1895:{\displaystyle {\mathcal {U}}=\{(V(f),f):f\in \Gamma ({\mathcal {O}}(d))\}}
2227:) and τ is universal among such natural transformations. More concretely,
50:) whose points represent algebro-geometric objects of some fixed kind, or
4409:
4298:
4293:
4023:
4018:
3955:
3871:
2888:
2586:
One can also enrich the problem by considering the moduli stack of genus
1397:{\displaystyle i^{*}{\mathcal {O}}_{\mathbf {P} _{\mathbb {Z} }^{n}}(1)}
107:) by varying 0 ≤ θ < π or as a quotient space of
4028:
4008:
3965:
3960:
3673:
3416:
3048:
2852:
3346:, Neue Folge, Band 34 Springer-Verlag, Berlin-New York 1965 vi+145 pp
2265:(regarded as families over a point) correspond to the same point of
3596:
4000:
489:
which all don't vanish at the same time. This means, given a point
94:
1994:
This is the standard concept. Heuristically, if we have a space
115:
For example, consider how to describe the collection of lines in
3729:
3558:
3533:
3508:
2337:× {1} via a nontrivial automorphism. Now if a fine moduli space
482:{\displaystyle s_{0},\ldots ,s_{n}\in \Gamma (X,{\mathcal {L}})}
3733:
2734:
of genus 1 curves with one marked point. This is the stack of
1545:) is a projective algebraic variety which parametrizes degree
753:{\displaystyle \circ x=\in \mathbf {P} _{\mathbb {Z} }^{n}(R)}
2703:
2650:
2612:
2554:
2515:
2465:
2425:
1872:
1820:
1775:
1727:
1724:
1721:
1718:
1479:
1358:
1243:
1177:
1128:
928:
917:
833:
778:
471:
371:
3298:
Moduli stacks in P-adic modular forms and
Langlands program
3227:"algebraic geometry - What does projective space classify?"
2742:, which are meromorphic sections of bundles on this stack.
178:). However, this map is two-to-one, so we want to identify
119:
which intersect the origin. We want to assign to each line
3587:. Graduate Texts in Mathematics. Vol. 187. New York:
3388:"The irreducibility of the space of curves of given genus"
3016:
by an object defined over a finitely generated ring. The
2575:
has dimension 0. The coarse moduli spaces have dimension 3
252:
is a moduli space that parametrizes the space of lines in
228:) as a moduli space of lines that intersect the origin in
2446:
classifies families of smooth projective curves of genus
2381:, but in many cases, they have a natural structure of an
2170:
carries a universal family; this family is the family on
2781:
has been achieved by restricting to a special class of
940:{\displaystyle \phi :{\mathcal {L}}\to {\mathcal {L}}'}
2985:
Another general approach is primarily associated with
2301:, while a coarse moduli space only has the base space
2120:
the set of all suitable families of objects with base
1652:) corresponds to a closed subscheme of a fixed scheme
1331:{\displaystyle i:X\to \mathbb {P} _{\mathbb {Z} }^{n}}
1172:
3001:
theorems to put these together into an object over a
2698:
2645:
2608:
2550:
2511:
2460:
2421:
1960:
1940:
1911:
1817:
1714:
1682:
1662:
1506:
1476:
1410:
1344:
1296:
1086:
1063:
1008:
953:
908:
772:
621:
547:
498:
424:
398:
368:
332:
312:
3327:
Séminaire Henri Cartan 13 No. 1, Exposés No. 7 and 8
2350:
some non-trivial families of objects they classify.
4431:
4408:
4385:
4332:
4217:
4125:
4067:
3999:
3948:
3915:
3810:
3767:
2325:× can be made into a twisted family on the circle
1934:is the associated projective scheme for the degree
763:
Then, two line bundles with sections are equivalent
2726:
2692:A case of particular interest is the moduli stack
2673:
2631:
2567:
2528:
2482:
2438:
2215:if there exists a natural transformation τ :
1966:
1946:
1926:
1894:
1797:
1697:
1668:
1518:
1492:
1462:
1396:
1330:
1279:
1069:
1046:
991:
939:
891:
752:
601:
527:
481:
410:
384:
354:
318:
3182:"Moduli Spaces of Curves: Classical and Tropical"
3033:if we are being careful) if not always a scheme.
3470:. Annals of Mathematics Studies. Vol. 108.
3344:Ergebnisse der Mathematik und ihrer Grenzgebiete
2727:{\displaystyle {\overline {\mathcal {M}}}_{1,1}}
2674:{\displaystyle {\overline {\mathcal {M}}}_{g,n}}
2146:, i.e., there is a natural isomorphism τ :
2116:from schemes to sets, which assigns to a scheme
174:) in the collection (which joins the origin and
146:We can also describe the collection of lines in
3630:Quasi-Projective Moduli for Polarized Manifolds
3273:"Algebraic Stacks and Moduli of Vector Bundles"
2907:, often described as a subscheme of a suitable
2112:More precisely, suppose that we have a functor
355:{\displaystyle \mathbf {P} _{\mathbb {Z} }^{n}}
2738:, and is the natural home of the much studied
2483:{\displaystyle {\overline {\mathcal {M}}}_{g}}
2166:) is the functor of points. This implies that
127:) with 0 ≤ θ < π radians. The set of lines
3745:
3051:to refer specifically to the moduli space of
2357:one can consider the category of families on
2321:is some geometric object, the trivial family
2285:In other words, a fine moduli space includes
1463:{\displaystyle i^{*}x_{0},\ldots ,i^{*}x_{n}}
8:
3703:(2011). "Moduli Problems for Ring Spectra".
2789:are used, for which he was awarded the 2018
2013:, then we can assemble these objects into a
1889:
1828:
1644:) is a moduli scheme. Every closed point of
3047:The term moduli space is sometimes used in
2974:in the Hilbert scheme has an action of PGL(
2081:if any family of algebro-geometric objects
2006:corresponds to an algebro-geometric object
999:. This means the associated moduli functor
306:Whenever there is an embedding of a scheme
198:/~ where the topology on this space is the
3752:
3738:
3730:
1613:curves as a subset of the space of degree
362:, the embedding is given by a line bundle
256:which pass through the origin. Similarly,
3406:
3203:"Lemma 27.13.1 (01NE)—The Stacks project"
2712:
2702:
2700:
2697:
2659:
2649:
2647:
2644:
2617:
2611:
2610:
2607:
2559:
2553:
2552:
2549:
2520:
2514:
2513:
2510:
2474:
2464:
2462:
2459:
2450:, together with their isomorphisms. When
2430:
2424:
2423:
2420:
2109:which is the base of a universal family.
1959:
1939:
1910:
1871:
1870:
1819:
1818:
1816:
1774:
1773:
1760:
1759:
1747:
1743:
1742:
1732:
1717:
1716:
1713:
1689:
1685:
1684:
1681:
1661:
1505:
1478:
1477:
1475:
1470:. Conversely, given an ample line bundle
1454:
1444:
1425:
1415:
1409:
1377:
1372:
1371:
1370:
1365:
1363:
1357:
1356:
1349:
1343:
1322:
1317:
1316:
1315:
1311:
1310:
1295:
1269:
1255:
1242:
1241:
1220:
1201:
1188:
1176:
1175:
1171:
1159:
1140:
1127:
1126:
1100:
1095:
1094:
1093:
1088:
1085:
1062:
1039:
1031:
1022:
1017:
1016:
1015:
1010:
1007:
980:
964:
952:
927:
926:
916:
915:
907:
874:
852:
832:
831:
812:
793:
777:
776:
771:
735:
730:
729:
728:
723:
701:
673:
648:
629:
620:
593:
588:
587:
586:
581:
563:
549:
548:
546:
505:
497:
470:
469:
448:
429:
423:
397:
370:
369:
367:
346:
341:
340:
339:
334:
331:
311:
3355:Mumford, David; Fogarty, J.; Kirwan, F.
3136:Moduli spaces of K-stable Fano varieties
3066:Moduli spaces also appear in physics in
2982:by the projective general linear group.
2899:the moduli problem under consideration.
2836:. This stack has been most studied when
1705:. This is given by the projective bundle
1609:, we obtain a parameter space of degree
3262:(Vol. 158). Cambridge University Press.
3172:
3151:Moduli of semistable sheaves on a curve
2954:> 2. A smooth curve together with a
528:{\displaystyle x:{\text{Spec}}(R)\to X}
2879:Methods for constructing moduli spaces
1526:sections gives an embedding as above.
70:first used the term "moduli" in 1857.
3059:, or to the moduli space of possible
1590:(2, 4), the Grassmannian of lines in
1257: form a basis of global sections
260:is the space of all complex lines in
7:
4150:Bogomol'nyi–Prasad–Sommerfield bound
3662:Publications Mathématiques de l'IHÉS
3468:Arithmetic Moduli of Elliptic Curves
3395:Publications Mathématiques de l'IHÉS
3078:of various algebraic moduli spaces.
2871:Simple geodesics and Weil-Petersson
2859:has been found to be significant in
2632:{\displaystyle {\mathcal {M}}_{g,n}}
1553:. It is constructed as follows. Let
326:into the universal projective space
2041:bundle whose fiber at any point ∊
1493:{\displaystyle {\mathcal {L}}\to X}
1338:gives the globally generated sheaf
992:{\displaystyle \phi (s_{i})=s_{i}'}
385:{\displaystyle {\mathcal {L}}\to X}
2774:, now known as KSB moduli spaces.
2568:{\displaystyle {\mathcal {M}}_{1}}
2529:{\displaystyle {\mathcal {M}}_{0}}
2493:Both stacks above have dimension 3
2439:{\displaystyle {\mathcal {M}}_{g}}
2174:corresponding to the identity map
2025:. (For example, the Grassmannian
1864:
1767:
1676:hypersurfaces of projective space
1229:
457:
241:Projective space and Grassmannians
25:
3429:Degeneration of Abelian Varieties
2993:. This means first constructing
2755:. This is the problem underlying
2105:. A fine moduli space is a space
1565:, then consider all the lines in
294:-dimensional linear subspaces of
2997:deformations, then appealing to
2053:) is simply the linear subspace
1986:to represent geometric objects.
1698:{\displaystyle \mathbb {P} ^{n}}
1366:
1089:
1011:
724:
582:
335:
42:is a geometric space (usually a
4347:Eleven-dimensional supergravity
3131:Moduli stack of elliptic curves
2875:of bordered Riemann surfaces.
2375:categories fibred in groupoids
2369:the groupoid of families over
1921:
1915:
1886:
1883:
1877:
1867:
1852:
1843:
1837:
1831:
1808:with universal family given by
1792:
1789:
1786:
1780:
1770:
1764:
1753:
1738:
1617:divisors of the Grassmannian:
1484:
1391:
1385:
1306:
1248:
1232:
1182:
1165:
1123:
1112:
1106:
1036:
970:
957:
922:
886:
883:
845:
827:
821:
818:
786:
773:
747:
741:
716:
713:
707:
685:
679:
666:
654:
622:
577:
574:
568:
554:
519:
516:
510:
476:
460:
376:
1:
3795:Second superstring revolution
3014:Artin's approximation theorem
2231:is a coarse moduli space for
4289:Generalized complex manifold
3790:First superstring revolution
3161:Moduli of semistable sheaves
2707:
2654:
2469:
902:iff there is an isomorphism
538:there is an associated point
264:passing through the origin.
158:and notice that every point
131:so parametrized is known as
2685: − 3 +
2602:-marked points are denoted
2365:which assigns to any space
290:is the moduli space of all
4956:
3887:Non-critical string theory
3713:10.1142/9789814324359_0088
3574:Other articles and sources
3472:Princeton University Press
3357:Geometric invariant theory
3340:Geometric invariant theory
3231:Mathematics Stack Exchange
3126:Moduli of algebraic curves
3040:
3005:base. Next, an appeal to
2941:geometric invariant theory
2867:Volume of the moduli space
2411:Moduli of algebraic curves
2408:
3437:10.1007/978-3-662-02632-8
3427:; Chai, Ching-Li (1990).
3386:; Mumford, David (1969).
3053:vacuum expectation values
1569:that intersect the curve
612:given by the compositions
4423:Introduction to M-theory
4117:Wess–Zumino–Witten model
4059:Hanany–Witten transition
3785:History of string theory
3688:Inventiones Mathematicae
3653:Simpson, Carlos (1994).
3583:; Morrison, Ian (1998).
3207:stacks.math.columbia.edu
3068:topological field theory
3010:formal existence theorem
2873:volumes of moduli spaces
2808:Moduli of vector bundles
2772:Nicholas Shepherd-Barron
258:complex projective space
18:Moduli of vector bundles
4102:Vertex operator algebra
3802:String theory landscape
3316:Grothendieck, Alexander
3260:Lectures on K3 surfaces
3156:Kontsevich moduli space
2681:), and have dimension 3
1954:homogeneous polynomial
1598:varies, by associating
220:Thus, when we consider
4400:AdS/CFT correspondence
4155:Exceptional Lie groups
4097:Superconformal algebra
4069:Conformal field theory
3940:Montonen–Olive duality
3892:Non-linear sigma model
3707:. pp. 1099–1125.
3258:Huybrechts, D., 2016.
3072:Feynman path integrals
2956:complete linear system
2753:Siegel modular variety
2728:
2675:
2633:
2579:−3 as the stacks when
2569:
2530:
2484:
2440:
2390:moduli space of curves
2277:are isomorphic. Thus,
1968:
1948:
1928:
1903:
1896:
1806:
1799:
1699:
1670:
1520:
1500:globally generated by
1494:
1464:
1398:
1332:
1288:
1281:
1190: is a line bundle
1071:
1055:
1048:
993:
941:
900:
893:
761:
754:
610:
603:
536:
529:
483:
412:
386:
356:
320:
112:
4395:Holographic principle
4362:Type IIB supergravity
4357:Type IIA supergravity
4209:-form electrodynamics
3828:Bosonic string theory
3041:Further information:
2729:
2676:
2634:
2570:
2531:
2485:
2441:
2409:Further information:
2293:and universal family
2243:gives rise to a map φ
1998:for which each point
1969:
1949:
1929:
1897:
1810:
1800:
1707:
1700:
1671:
1557:be a curve of degree
1521:
1495:
1465:
1399:
1333:
1282:
1079:
1072:
1049:
1001:
994:
942:
894:
765:
755:
614:
604:
540:
530:
491:
484:
413:
387:
357:
321:
247:real projective space
98:
81:positive real numbers
4314:Hořava–Witten theory
4261:Hyperkähler manifold
3949:Particles and fields
3897:Tachyon condensation
3882:Matrix string theory
3076:intersection numbers
3070:, where one can use
3023:equivalence relation
2943:(GIT), developed by
2696:
2643:
2606:
2548:
2509:
2501:−3 parameters, when
2458:
2419:
2257:and any two objects
2199:Coarse moduli spaces
2085:over any base space
1958:
1938:
1927:{\displaystyle V(f)}
1909:
1815:
1712:
1680:
1660:
1504:
1474:
1408:
1342:
1294:
1084:
1061:
1006:
951:
906:
770:
619:
545:
496:
422:
396:
366:
330:
310:
282:) of a vector space
267:More generally, the
141:real projective line
139:) and is called the
4352:Type I supergravity
4256:Calabi–Yau manifold
4251:Ricci-flat manifold
4230:Kaluza–Klein theory
3971:Ramond–Ramond field
3877:String field theory
3636:. Springer Verlag.
2999:prorepresentability
2857:principal G-bundles
2851:In applications to
2757:Siegel modular form
2746:Moduli of varieties
2373:. The use of these
2209:coarse moduli space
2097:along a unique map
1573:. This is a degree
1519:{\displaystyle n+1}
1382:
1327:
1105:
1027:
988:
882:
860:
740:
598:
411:{\displaystyle n+1}
351:
52:isomorphism classes
4319:K-theory (physics)
4196:ADE classification
3833:Superstring theory
3674:10.1007/bf02698887
3462:Katz, Nicholas M;
3417:10.1007/bf02684599
3377:Early applications
3309:Fundamental papers
3103:Deformation theory
3087:Construction tools
3061:string backgrounds
2991:deformation theory
2893:Teichmüller spaces
2724:
2671:
2629:
2590:nodal curves with
2565:
2526:
2480:
2436:
1990:Fine moduli spaces
1964:
1944:
1924:
1892:
1795:
1695:
1666:
1516:
1490:
1460:
1394:
1364:
1328:
1309:
1277:
1262:
1087:
1067:
1044:
1009:
989:
976:
937:
889:
870:
848:
750:
722:
599:
580:
525:
479:
408:
382:
352:
333:
316:
113:
36:algebraic geometry
4922:
4921:
4704:van Nieuwenhuizen
4240:Why 10 dimensions
4145:Chern–Simons form
4112:Kac–Moody algebra
4092:Conformal algebra
4087:Conformal anomaly
3981:Magnetic monopole
3976:Kalb–Ramond field
3818:Nambu–Goto action
3722:978-981-4324-30-4
3681:Maryam Mirzakhani
3643:978-3-540-59255-6
3606:978-0-387-98429-2
3567:978-3-03719-103-3
3542:978-3-03719-055-5
3517:978-3-03719-029-6
3481:978-0-691-08352-0
3446:978-3-540-52015-3
3304:Research articles
3113:Artin's criterion
2935:by the action of
2885:categories fibred
2831:algebraic variety
2802:Abelian varieties
2759:theory. See also
2710:
2657:
2472:
2415:The moduli stack
2341:existed, the map
2130:fine moduli space
2037:) carries a rank
1967:{\displaystyle f}
1947:{\displaystyle d}
1669:{\displaystyle d}
1258:
1191:
1070:{\displaystyle X}
1042:
1034:
566:
557:
508:
319:{\displaystyle X}
200:quotient topology
16:(Redirected from
4947:
4940:Invariant theory
4432:String theorists
4372:Lie superalgebra
4324:Twisted K-theory
4282:Spin(7)-manifold
4235:Compactification
4077:Virasoro algebra
3860:Heterotic string
3754:
3747:
3740:
3731:
3726:
3677:
3659:
3647:
3635:
3618:
3585:Moduli of Curves
3498:Other references
3493:
3458:
3420:
3410:
3392:
3330:
3324:
3280:
3279:
3277:
3269:
3263:
3256:
3250:
3247:
3241:
3240:
3238:
3237:
3223:
3217:
3216:
3214:
3213:
3199:
3193:
3192:
3186:
3177:
3043:moduli (physics)
2846:Jacobian variety
2804:are understood.
2733:
2731:
2730:
2725:
2723:
2722:
2711:
2706:
2701:
2680:
2678:
2677:
2672:
2670:
2669:
2658:
2653:
2648:
2638:
2636:
2635:
2630:
2628:
2627:
2616:
2615:
2574:
2572:
2571:
2566:
2564:
2563:
2558:
2557:
2535:
2533:
2532:
2527:
2525:
2524:
2519:
2518:
2489:
2487:
2486:
2481:
2479:
2478:
2473:
2468:
2463:
2445:
2443:
2442:
2437:
2435:
2434:
2429:
2428:
2405:Moduli of curves
2400:Further examples
2379:algebraic spaces
2211:for the functor
2132:for the functor
1973:
1971:
1970:
1965:
1953:
1951:
1950:
1945:
1933:
1931:
1930:
1925:
1901:
1899:
1898:
1893:
1876:
1875:
1824:
1823:
1804:
1802:
1801:
1796:
1779:
1778:
1763:
1752:
1751:
1746:
1737:
1736:
1731:
1730:
1704:
1702:
1701:
1696:
1694:
1693:
1688:
1675:
1673:
1672:
1667:
1525:
1523:
1522:
1517:
1499:
1497:
1496:
1491:
1483:
1482:
1469:
1467:
1466:
1461:
1459:
1458:
1449:
1448:
1430:
1429:
1420:
1419:
1403:
1401:
1400:
1395:
1384:
1383:
1381:
1376:
1375:
1369:
1362:
1361:
1354:
1353:
1337:
1335:
1334:
1329:
1326:
1321:
1320:
1314:
1286:
1284:
1283:
1278:
1273:
1268:
1264:
1263:
1259:
1256:
1247:
1246:
1225:
1224:
1206:
1205:
1192:
1189:
1181:
1180:
1164:
1163:
1145:
1144:
1132:
1131:
1104:
1099:
1098:
1092:
1076:
1074:
1073:
1068:
1053:
1051:
1050:
1045:
1043:
1040:
1035:
1032:
1026:
1021:
1020:
1014:
998:
996:
995:
990:
984:
969:
968:
946:
944:
943:
938:
936:
932:
931:
921:
920:
898:
896:
895:
890:
878:
856:
841:
837:
836:
817:
816:
798:
797:
782:
781:
759:
757:
756:
751:
739:
734:
733:
727:
706:
705:
678:
677:
653:
652:
634:
633:
608:
606:
605:
600:
597:
592:
591:
585:
567:
564:
559:
558:
550:
534:
532:
531:
526:
509:
506:
488:
486:
485:
480:
475:
474:
453:
452:
434:
433:
417:
415:
414:
409:
391:
389:
388:
383:
375:
374:
361:
359:
358:
353:
350:
345:
344:
338:
325:
323:
322:
317:
68:Bernhard Riemann
56:algebraic curves
34:, in particular
21:
4955:
4954:
4950:
4949:
4948:
4946:
4945:
4944:
4925:
4924:
4923:
4918:
4427:
4404:
4381:
4328:
4276:
4246:Kähler manifold
4213:
4190:
4183:
4176:
4169:
4162:
4121:
4082:Mirror symmetry
4063:
4049:Brane cosmology
3995:
3944:
3911:
3867:N=2 superstring
3853:Type IIB string
3848:Type IIA string
3823:Polyakov action
3806:
3763:
3758:
3723:
3699:
3696:
3657:
3652:
3644:
3633:
3625:Viehweg, Eckart
3623:
3607:
3589:Springer Verlag
3579:
3576:
3500:
3482:
3461:
3447:
3423:
3390:
3384:Deligne, Pierre
3382:
3379:
3322:
3314:
3311:
3306:
3289:
3284:
3283:
3275:
3271:
3270:
3266:
3257:
3253:
3248:
3244:
3235:
3233:
3225:
3224:
3220:
3211:
3209:
3201:
3200:
3196:
3184:
3179:
3178:
3174:
3169:
3122:
3089:
3084:
3074:to compute the
3045:
3039:
3031:algebraic stack
3027:algebraic space
2881:
2869:
2817:
2810:
2761:Shimura variety
2748:
2736:elliptic curves
2699:
2694:
2693:
2646:
2641:
2640:
2609:
2604:
2603:
2551:
2546:
2545:
2512:
2507:
2506:
2461:
2456:
2455:
2422:
2417:
2416:
2413:
2407:
2402:
2383:algebraic stack
2363:fibred category
2329:by identifying
2311:
2269:if and only if
2248:
2201:
2182:
2011:
1992:
1980:
1956:
1955:
1936:
1935:
1907:
1906:
1813:
1812:
1741:
1715:
1710:
1709:
1683:
1678:
1677:
1658:
1657:
1631:
1607:
1584:
1532:
1502:
1501:
1472:
1471:
1450:
1440:
1421:
1411:
1406:
1405:
1355:
1345:
1340:
1339:
1292:
1291:
1261:
1260:
1252:
1251:
1216:
1197:
1194:
1193:
1155:
1136:
1122:
1118:
1082:
1081:
1059:
1058:
1057:sends a scheme
1004:
1003:
960:
949:
948:
925:
904:
903:
830:
808:
789:
768:
767:
697:
669:
644:
625:
617:
616:
543:
542:
494:
493:
444:
425:
420:
419:
394:
393:
364:
363:
328:
327:
308:
307:
304:
243:
238:
202:induced by the
76:
48:algebraic stack
28:
23:
22:
15:
12:
11:
5:
4953:
4951:
4943:
4942:
4937:
4927:
4926:
4920:
4919:
4917:
4916:
4911:
4906:
4901:
4896:
4891:
4886:
4881:
4876:
4871:
4866:
4861:
4856:
4851:
4846:
4841:
4836:
4831:
4826:
4821:
4816:
4811:
4806:
4801:
4796:
4791:
4786:
4781:
4776:
4771:
4766:
4761:
4756:
4754:Randjbar-Daemi
4751:
4746:
4741:
4736:
4731:
4726:
4721:
4716:
4711:
4706:
4701:
4696:
4691:
4686:
4681:
4676:
4671:
4666:
4661:
4656:
4651:
4646:
4641:
4636:
4631:
4626:
4621:
4616:
4611:
4606:
4601:
4596:
4591:
4586:
4581:
4576:
4571:
4566:
4561:
4556:
4551:
4546:
4541:
4536:
4531:
4526:
4521:
4516:
4511:
4506:
4501:
4496:
4491:
4486:
4481:
4476:
4471:
4466:
4461:
4456:
4451:
4446:
4441:
4435:
4433:
4429:
4428:
4426:
4425:
4420:
4414:
4412:
4406:
4405:
4403:
4402:
4397:
4391:
4389:
4383:
4382:
4380:
4379:
4377:Lie supergroup
4374:
4369:
4364:
4359:
4354:
4349:
4344:
4338:
4336:
4330:
4329:
4327:
4326:
4321:
4316:
4311:
4306:
4301:
4296:
4291:
4286:
4285:
4284:
4279:
4274:
4270:
4269:
4268:
4258:
4248:
4243:
4237:
4232:
4227:
4221:
4219:
4215:
4214:
4212:
4211:
4203:
4198:
4193:
4188:
4181:
4174:
4167:
4160:
4152:
4147:
4142:
4137:
4131:
4129:
4123:
4122:
4120:
4119:
4114:
4109:
4104:
4099:
4094:
4089:
4084:
4079:
4073:
4071:
4065:
4064:
4062:
4061:
4056:
4054:Quiver diagram
4051:
4046:
4041:
4036:
4031:
4026:
4021:
4016:
4011:
4005:
4003:
3997:
3996:
3994:
3993:
3988:
3983:
3978:
3973:
3968:
3963:
3958:
3952:
3950:
3946:
3945:
3943:
3942:
3937:
3932:
3927:
3921:
3919:
3917:String duality
3913:
3912:
3910:
3909:
3904:
3899:
3894:
3889:
3884:
3879:
3874:
3869:
3864:
3863:
3862:
3857:
3856:
3855:
3850:
3843:Type II string
3840:
3830:
3825:
3820:
3814:
3812:
3808:
3807:
3805:
3804:
3799:
3798:
3797:
3792:
3782:
3780:Cosmic strings
3777:
3771:
3769:
3765:
3764:
3759:
3757:
3756:
3749:
3742:
3734:
3728:
3727:
3721:
3695:
3694:External links
3692:
3691:
3690:
3678:
3649:
3648:
3642:
3620:
3619:
3605:
3597:10.1007/b98867
3575:
3572:
3571:
3570:
3551:
3526:
3499:
3496:
3495:
3494:
3480:
3459:
3445:
3425:Faltings, Gerd
3421:
3408:10.1.1.589.288
3378:
3375:
3374:
3373:
3353:
3336:Mumford, David
3332:
3331:
3310:
3307:
3305:
3302:
3301:
3300:
3295:
3288:
3285:
3282:
3281:
3264:
3251:
3242:
3218:
3194:
3180:Chan, Melody.
3171:
3170:
3168:
3165:
3164:
3163:
3158:
3153:
3148:
3146:Picard functor
3143:
3138:
3133:
3128:
3121:
3118:
3117:
3116:
3110:
3105:
3100:
3095:
3093:Hilbert scheme
3088:
3085:
3083:
3080:
3038:
3035:
3007:Grothendieck's
2909:Hilbert scheme
2880:
2877:
2868:
2865:
2827:vector bundles
2813:
2809:
2806:
2787:Caucher Birkar
2779:Fano varieties
2747:
2744:
2721:
2718:
2715:
2709:
2705:
2668:
2665:
2662:
2656:
2652:
2626:
2623:
2620:
2614:
2562:
2556:
2542:
2541:
2523:
2517:
2477:
2471:
2467:
2433:
2427:
2406:
2403:
2401:
2398:
2310:
2307:
2244:
2235:if any family
2200:
2197:
2178:
2073:. We say that
2069:of the family
2009:
1991:
1988:
1979:
1976:
1963:
1943:
1923:
1920:
1917:
1914:
1891:
1888:
1885:
1882:
1879:
1874:
1869:
1866:
1863:
1860:
1857:
1854:
1851:
1848:
1845:
1842:
1839:
1836:
1833:
1830:
1827:
1822:
1794:
1791:
1788:
1785:
1782:
1777:
1772:
1769:
1766:
1762:
1758:
1755:
1750:
1745:
1740:
1735:
1729:
1726:
1723:
1720:
1692:
1687:
1665:
1635:Hilbert scheme
1630:
1629:Hilbert scheme
1627:
1605:
1582:
1531:
1528:
1515:
1512:
1509:
1489:
1486:
1481:
1457:
1453:
1447:
1443:
1439:
1436:
1433:
1428:
1424:
1418:
1414:
1404:with sections
1393:
1390:
1387:
1380:
1374:
1368:
1360:
1352:
1348:
1325:
1319:
1313:
1308:
1305:
1302:
1299:
1276:
1272:
1267:
1254:
1253:
1250:
1245:
1240:
1237:
1234:
1231:
1228:
1223:
1219:
1215:
1212:
1209:
1204:
1200:
1196:
1195:
1187:
1184:
1179:
1174:
1173:
1170:
1167:
1162:
1158:
1154:
1151:
1148:
1143:
1139:
1135:
1130:
1125:
1121:
1117:
1114:
1111:
1108:
1103:
1097:
1091:
1066:
1038:
1030:
1025:
1019:
1013:
987:
983:
979:
975:
972:
967:
963:
959:
956:
935:
930:
924:
919:
914:
911:
888:
885:
881:
877:
873:
869:
866:
863:
859:
855:
851:
847:
844:
840:
835:
829:
826:
823:
820:
815:
811:
807:
804:
801:
796:
792:
788:
785:
780:
775:
749:
746:
743:
738:
732:
726:
721:
718:
715:
712:
709:
704:
700:
696:
693:
690:
687:
684:
681:
676:
672:
668:
665:
662:
659:
656:
651:
647:
643:
640:
637:
632:
628:
624:
596:
590:
584:
579:
576:
573:
570:
562:
556:
553:
524:
521:
518:
515:
512:
504:
501:
478:
473:
468:
465:
462:
459:
456:
451:
447:
443:
440:
437:
432:
428:
407:
404:
401:
381:
378:
373:
349:
343:
337:
315:
303:
300:
242:
239:
237:
236:Basic examples
234:
75:
72:
26:
24:
14:
13:
10:
9:
6:
4:
3:
2:
4952:
4941:
4938:
4936:
4935:Moduli theory
4933:
4932:
4930:
4915:
4912:
4910:
4907:
4905:
4902:
4900:
4899:Zamolodchikov
4897:
4895:
4894:Zamolodchikov
4892:
4890:
4887:
4885:
4882:
4880:
4877:
4875:
4872:
4870:
4867:
4865:
4862:
4860:
4857:
4855:
4852:
4850:
4847:
4845:
4842:
4840:
4837:
4835:
4832:
4830:
4827:
4825:
4822:
4820:
4817:
4815:
4812:
4810:
4807:
4805:
4802:
4800:
4797:
4795:
4792:
4790:
4787:
4785:
4782:
4780:
4777:
4775:
4772:
4770:
4767:
4765:
4762:
4760:
4757:
4755:
4752:
4750:
4747:
4745:
4742:
4740:
4737:
4735:
4732:
4730:
4727:
4725:
4722:
4720:
4717:
4715:
4712:
4710:
4707:
4705:
4702:
4700:
4697:
4695:
4692:
4690:
4687:
4685:
4682:
4680:
4677:
4675:
4672:
4670:
4667:
4665:
4662:
4660:
4657:
4655:
4652:
4650:
4647:
4645:
4642:
4640:
4637:
4635:
4632:
4630:
4627:
4625:
4622:
4620:
4617:
4615:
4612:
4610:
4607:
4605:
4602:
4600:
4597:
4595:
4592:
4590:
4587:
4585:
4582:
4580:
4577:
4575:
4572:
4570:
4567:
4565:
4562:
4560:
4557:
4555:
4552:
4550:
4547:
4545:
4542:
4540:
4537:
4535:
4532:
4530:
4527:
4525:
4522:
4520:
4517:
4515:
4512:
4510:
4507:
4505:
4502:
4500:
4497:
4495:
4492:
4490:
4487:
4485:
4482:
4480:
4477:
4475:
4472:
4470:
4467:
4465:
4462:
4460:
4457:
4455:
4452:
4450:
4447:
4445:
4442:
4440:
4437:
4436:
4434:
4430:
4424:
4421:
4419:
4418:Matrix theory
4416:
4415:
4413:
4411:
4407:
4401:
4398:
4396:
4393:
4392:
4390:
4388:
4384:
4378:
4375:
4373:
4370:
4368:
4365:
4363:
4360:
4358:
4355:
4353:
4350:
4348:
4345:
4343:
4340:
4339:
4337:
4335:
4334:Supersymmetry
4331:
4325:
4322:
4320:
4317:
4315:
4312:
4310:
4307:
4305:
4302:
4300:
4297:
4295:
4292:
4290:
4287:
4283:
4280:
4278:
4271:
4267:
4264:
4263:
4262:
4259:
4257:
4254:
4253:
4252:
4249:
4247:
4244:
4241:
4238:
4236:
4233:
4231:
4228:
4226:
4223:
4222:
4220:
4216:
4210:
4208:
4204:
4202:
4199:
4197:
4194:
4191:
4184:
4177:
4170:
4163:
4156:
4153:
4151:
4148:
4146:
4143:
4141:
4138:
4136:
4133:
4132:
4130:
4128:
4124:
4118:
4115:
4113:
4110:
4108:
4105:
4103:
4100:
4098:
4095:
4093:
4090:
4088:
4085:
4083:
4080:
4078:
4075:
4074:
4072:
4070:
4066:
4060:
4057:
4055:
4052:
4050:
4047:
4045:
4042:
4040:
4037:
4035:
4032:
4030:
4027:
4025:
4022:
4020:
4017:
4015:
4012:
4010:
4007:
4006:
4004:
4002:
3998:
3992:
3989:
3987:
3986:Dual graviton
3984:
3982:
3979:
3977:
3974:
3972:
3969:
3967:
3964:
3962:
3959:
3957:
3954:
3953:
3951:
3947:
3941:
3938:
3936:
3933:
3931:
3928:
3926:
3923:
3922:
3920:
3918:
3914:
3908:
3905:
3903:
3902:RNS formalism
3900:
3898:
3895:
3893:
3890:
3888:
3885:
3883:
3880:
3878:
3875:
3873:
3870:
3868:
3865:
3861:
3858:
3854:
3851:
3849:
3846:
3845:
3844:
3841:
3839:
3838:Type I string
3836:
3835:
3834:
3831:
3829:
3826:
3824:
3821:
3819:
3816:
3815:
3813:
3809:
3803:
3800:
3796:
3793:
3791:
3788:
3787:
3786:
3783:
3781:
3778:
3776:
3773:
3772:
3770:
3766:
3762:
3761:String theory
3755:
3750:
3748:
3743:
3741:
3736:
3735:
3732:
3724:
3718:
3714:
3710:
3706:
3702:
3698:
3697:
3693:
3689:
3686:
3682:
3679:
3675:
3671:
3667:
3663:
3656:
3651:
3650:
3645:
3639:
3632:
3631:
3626:
3622:
3621:
3616:
3612:
3608:
3602:
3598:
3594:
3590:
3586:
3582:
3578:
3577:
3573:
3568:
3564:
3560:
3556:
3552:
3550:
3547:
3543:
3539:
3535:
3531:
3527:
3525:
3522:
3518:
3514:
3510:
3506:
3502:
3501:
3497:
3491:
3487:
3483:
3477:
3473:
3469:
3465:
3460:
3456:
3452:
3448:
3442:
3438:
3434:
3430:
3426:
3422:
3418:
3414:
3409:
3404:
3400:
3396:
3389:
3385:
3381:
3380:
3376:
3372:
3371:3-540-56963-4
3368:
3365:
3362:
3358:
3354:
3352:
3349:
3345:
3341:
3337:
3334:
3333:
3328:
3321:
3318:(1960–1961).
3317:
3313:
3312:
3308:
3303:
3299:
3296:
3294:
3293:Moduli theory
3291:
3290:
3286:
3274:
3268:
3265:
3261:
3255:
3252:
3246:
3243:
3232:
3228:
3222:
3219:
3208:
3204:
3198:
3195:
3190:
3183:
3176:
3173:
3166:
3162:
3159:
3157:
3154:
3152:
3149:
3147:
3144:
3142:
3141:Modular curve
3139:
3137:
3134:
3132:
3129:
3127:
3124:
3123:
3120:Moduli spaces
3119:
3114:
3111:
3109:
3106:
3104:
3101:
3099:
3096:
3094:
3091:
3090:
3086:
3081:
3079:
3077:
3073:
3069:
3064:
3062:
3058:
3057:scalar fields
3054:
3050:
3044:
3036:
3034:
3032:
3029:(actually an
3028:
3024:
3019:
3015:
3011:
3008:
3004:
3000:
2996:
2995:infinitesimal
2992:
2988:
2987:Michael Artin
2983:
2981:
2977:
2973:
2969:
2965:
2961:
2957:
2953:
2948:
2946:
2945:David Mumford
2942:
2938:
2934:
2930:
2926:
2922:
2918:
2914:
2910:
2906:
2900:
2898:
2894:
2890:
2886:
2878:
2876:
2874:
2866:
2864:
2862:
2858:
2854:
2849:
2847:
2843:
2842:Picard scheme
2839:
2835:
2832:
2828:
2825:
2821:
2816:
2807:
2805:
2803:
2799:
2794:
2792:
2788:
2784:
2780:
2775:
2773:
2769:
2764:
2762:
2758:
2754:
2745:
2743:
2741:
2740:modular forms
2737:
2719:
2716:
2713:
2690:
2688:
2684:
2666:
2663:
2660:
2624:
2621:
2618:
2601:
2597:
2593:
2589:
2584:
2582:
2578:
2560:
2539:
2538:
2537:
2521:
2504:
2500:
2496:
2491:
2475:
2453:
2449:
2431:
2412:
2404:
2399:
2397:
2395:
2391:
2386:
2384:
2380:
2376:
2372:
2368:
2364:
2360:
2356:
2351:
2348:
2344:
2340:
2336:
2332:
2328:
2324:
2320:
2316:
2315:automorphisms
2309:Moduli stacks
2308:
2306:
2304:
2300:
2296:
2292:
2289:a base space
2288:
2283:
2280:
2276:
2272:
2268:
2264:
2260:
2256:
2252:
2247:
2242:
2238:
2234:
2230:
2226:
2222:
2218:
2214:
2210:
2206:
2198:
2196:
2194:
2190:
2186:
2181:
2177:
2173:
2169:
2165:
2161:
2157:
2153:
2149:
2145:
2142:
2139:
2135:
2131:
2127:
2123:
2119:
2115:
2110:
2108:
2104:
2100:
2096:
2092:
2088:
2084:
2080:
2076:
2075:such a family
2072:
2068:
2064:
2060:
2056:
2052:
2048:
2044:
2040:
2036:
2032:
2028:
2024:
2020:
2016:
2012:
2005:
2001:
1997:
1989:
1987:
1985:
1977:
1975:
1961:
1941:
1918:
1912:
1902:
1880:
1861:
1858:
1855:
1849:
1846:
1840:
1834:
1825:
1809:
1805:
1783:
1756:
1748:
1733:
1706:
1690:
1663:
1655:
1651:
1647:
1643:
1639:
1636:
1628:
1626:
1624:
1620:
1616:
1612:
1608:
1601:
1597:
1593:
1589:
1585:
1579:
1576:
1572:
1568:
1564:
1560:
1556:
1552:
1548:
1544:
1540:
1537:
1529:
1527:
1513:
1510:
1507:
1487:
1455:
1451:
1445:
1441:
1437:
1434:
1431:
1426:
1422:
1416:
1412:
1388:
1378:
1350:
1346:
1323:
1303:
1300:
1297:
1287:
1274:
1270:
1265:
1238:
1235:
1226:
1221:
1217:
1213:
1210:
1207:
1202:
1198:
1185:
1168:
1160:
1156:
1152:
1149:
1146:
1141:
1137:
1133:
1119:
1115:
1109:
1101:
1078:
1064:
1054:
1028:
1023:
1000:
985:
981:
977:
973:
965:
961:
954:
933:
912:
909:
899:
879:
875:
871:
867:
864:
861:
857:
853:
849:
842:
838:
824:
813:
809:
805:
802:
799:
794:
790:
783:
764:
760:
744:
736:
719:
710:
702:
698:
694:
691:
688:
682:
674:
670:
663:
660:
657:
649:
645:
641:
638:
635:
630:
626:
613:
609:
594:
571:
560:
551:
539:
535:
522:
513:
502:
499:
490:
466:
463:
454:
449:
445:
441:
438:
435:
430:
426:
405:
402:
399:
379:
347:
313:
301:
299:
297:
293:
289:
286:over a field
285:
281:
277:
273:
270:
265:
263:
259:
255:
251:
248:
240:
235:
233:
231:
227:
223:
218:
216:
212:
208:
205:
201:
197:
193:
189:
185:
181:
177:
173:
169:
166:gives a line
165:
161:
157:
153:
149:
144:
142:
138:
134:
130:
126:
122:
118:
110:
106:
102:
99:Constructing
97:
93:
90:
84:
82:
73:
71:
69:
65:
64:formal moduli
61:
57:
53:
49:
45:
41:
37:
33:
19:
4444:Arkani-Hamed
4342:Supergravity
4309:Moduli space
4308:
4206:
4201:Dirac string
4127:Gauge theory
4107:Loop algebra
4044:Black string
3907:GS formalism
3704:
3665:
3661:
3629:
3584:
3467:
3464:Mazur, Barry
3428:
3398:
3394:
3356:
3339:
3326:
3267:
3259:
3254:
3245:
3234:. Retrieved
3230:
3221:
3210:. Retrieved
3206:
3197:
3188:
3175:
3108:GIT quotient
3065:
3055:of a set of
3046:
2998:
2984:
2979:
2975:
2971:
2967:
2963:
2959:
2951:
2949:
2936:
2932:
2928:
2924:
2920:
2916:
2904:
2901:
2896:
2882:
2870:
2861:gauge theory
2850:
2837:
2833:
2823:
2819:
2814:
2811:
2795:
2791:Fields medal
2776:
2768:János Kollár
2765:
2749:
2691:
2686:
2682:
2599:
2598:curves with
2595:
2591:
2587:
2585:
2580:
2576:
2543:
2502:
2498:
2494:
2492:
2451:
2447:
2414:
2394:moduli stack
2393:
2387:
2374:
2370:
2366:
2358:
2354:
2352:
2346:
2342:
2338:
2334:
2330:
2326:
2322:
2318:
2312:
2302:
2298:
2294:
2290:
2286:
2284:
2278:
2274:
2270:
2266:
2262:
2258:
2254:
2250:
2245:
2240:
2239:over a base
2236:
2232:
2228:
2224:
2220:
2216:
2212:
2208:
2204:
2202:
2192:
2188:
2184:
2179:
2175:
2171:
2167:
2163:
2159:
2155:
2151:
2147:
2143:
2137:
2133:
2129:
2125:
2121:
2117:
2113:
2111:
2106:
2102:
2098:
2094:
2086:
2082:
2078:
2070:
2066:
2065:is called a
2062:
2058:
2054:
2050:
2046:
2042:
2038:
2034:
2030:
2026:
2022:
2018:
2015:tautological
2007:
2003:
1999:
1995:
1993:
1983:
1981:
1904:
1811:
1807:
1708:
1653:
1649:
1645:
1641:
1637:
1632:
1622:
1618:
1614:
1610:
1603:
1599:
1595:
1591:
1587:
1580:
1574:
1570:
1566:
1562:
1558:
1554:
1550:
1546:
1542:
1538:
1536:Chow variety
1533:
1530:Chow variety
1289:
1080:
1056:
1002:
901:
766:
762:
615:
611:
541:
537:
492:
305:
295:
291:
287:
283:
279:
275:
271:
269:Grassmannian
266:
261:
253:
249:
244:
229:
225:
221:
219:
214:
210:
206:
204:quotient map
195:
191:
187:
183:
179:
175:
171:
167:
163:
159:
155:
151:
147:
145:
136:
132:
128:
124:
120:
116:
114:
108:
104:
100:
85:
77:
40:moduli space
39:
29:
4804:Silverstein
4304:Orientifold
4039:Black holes
4034:Black brane
3991:Dual photon
3581:Harris, Joe
3559:10.4171/103
3534:10.4171/055
3509:10.4171/029
3098:Quot scheme
2913:Quot scheme
2897:rigidifying
2829:on a fixed
2798:K3 surfaces
2333:× {0} with
1978:Definitions
58:of a fixed
32:mathematics
4929:Categories
4824:Strominger
4819:Steinhardt
4814:Staudacher
4729:Polchinski
4679:Nanopoulos
4639:Mandelstam
4619:Kontsevich
4459:Berenstein
4387:Holography
4367:Superspace
4266:K3 surface
4225:Worldsheet
4140:Instantons
3768:Background
3668:: 47–129.
3401:: 75–109.
3236:2020-09-12
3212:2020-09-12
3167:References
3037:In physics
2958:of degree
2822:) of rank
2141:represents
2124:. A space
2067:base space
1549:curves in
1077:to the set
947:such that
74:Motivation
4859:Veneziano
4739:Rajaraman
4634:Maldacena
4524:Gopakumar
4474:Dijkgraaf
4469:Curtright
4135:Anomalies
4014:NS5-brane
3935:U-duality
3930:S-duality
3925:T-duality
3701:Lurie, J.
3403:CiteSeerX
2889:groupoids
2708:¯
2655:¯
2470:¯
2158:), where
2079:universal
1865:Γ
1862:∈
1768:Γ
1485:→
1446:∗
1435:…
1417:∗
1351:∗
1307:→
1275:∼
1230:Γ
1227:∈
1211:…
1183:→
1150:…
1037:→
955:ϕ
923:→
910:ϕ
865:…
825:∼
803:…
720:∈
692:⋯
658:∘
639:⋯
578:→
555:^
520:→
458:Γ
455:∈
439:…
418:sections
377:→
186:to yield
4914:Zwiebach
4869:Verlinde
4864:Verlinde
4839:Townsend
4834:Susskind
4769:Sagnotti
4734:Polyakov
4689:Nekrasov
4654:Minwalla
4649:Martinec
4614:Knizhnik
4609:Klebanov
4604:Kapustin
4569:'t Hooft
4504:Fischler
4439:Aganagić
4410:M-theory
4299:Conifold
4294:Orbifold
4277:manifold
4218:Geometry
4024:M5-brane
4019:M2-brane
3956:Graviton
3872:F-theory
3627:(1995).
3466:(1985).
3329:. Paris.
3082:See also
3018:spectrum
2783:K-stable
2249: :
2091:pullback
986:′
934:′
880:′
858:′
839:′
4844:Trivedi
4829:Sundrum
4794:Shenker
4784:Seiberg
4779:Schwarz
4749:Randall
4709:Novikov
4699:Nielsen
4684:Năstase
4594:Kallosh
4579:Gibbons
4519:Gliozzi
4509:Friedan
4499:Ferrara
4484:Douglas
4479:Distler
4029:S-brane
4009:D-brane
3966:Tachyon
3961:Dilaton
3775:Strings
3683:(2007)
3615:1631825
3549:2524085
3524:2284826
3490:0772569
3455:1083353
3364:1304906
3351:0214602
3049:physics
2853:physics
2089:is the
2017:family
1594:. When
1578:divisor
4909:Zumino
4904:Zaslow
4889:Yoneya
4879:Witten
4799:Siegel
4774:Scherk
4744:Ramond
4719:Ooguri
4644:Marolf
4599:Kaluza
4584:Kachru
4574:Hořava
4564:Harvey
4559:Hanson
4544:Gubser
4534:Greene
4464:Bousso
4449:Atiyah
4001:Branes
3811:Theory
3719:
3640:
3613:
3603:
3565:
3540:
3515:
3488:
3478:
3453:
3443:
3405:
3369:
3003:formal
2962:> 2
1905:where
89:metric
46:or an
44:scheme
4849:Turok
4759:Roček
4724:Ovrut
4714:Olive
4694:Neveu
4674:Myers
4669:Mukhi
4659:Moore
4629:Linde
4624:Klein
4549:Gukov
4539:Gross
4529:Green
4514:Gates
4494:Dvali
4454:Banks
3658:(PDF)
3634:(PDF)
3391:(PDF)
3323:(PDF)
3287:Notes
3276:(PDF)
3185:(PDF)
2207:is a
2128:is a
2021:over
60:genus
4874:Wess
4854:Vafa
4764:Rohm
4664:Motl
4589:Kaku
4554:Guth
4489:Duff
3717:ISBN
3638:ISBN
3601:ISBN
3563:ISBN
3538:ISBN
3513:ISBN
3476:ISBN
3441:ISBN
3367:ISBN
2770:and
2639:(or
2287:both
2273:and
2261:and
2223:(−,
2162:(−,
2154:(−,
1646:Hilb
1638:Hilb
1633:The
1619:Chow
1539:Chow
1534:The
1041:Sets
565:Spec
507:Spec
392:and
245:The
194:) ≅
38:, a
4884:Yau
4809:Sơn
4789:Sen
3709:doi
3670:doi
3593:doi
3555:doi
3530:doi
3505:doi
3433:doi
3413:doi
3189:AMS
2931:of
2911:or
2887:in
2800:or
2793:.
2536:is
2221:Hom
2195:).
2185:Hom
2160:Hom
2152:Hom
2136:if
2093:of
2077:is
2061:.)
1625:).
1621:(d,
1602:to
1586:in
1561:in
1541:(d,
1033:Sch
217:).
182:~ −
30:In
4931::
4185:,
4178:,
4171:,
4164:,
3715:.
3666:79
3664:.
3660:.
3611:MR
3609:.
3599:.
3591:.
3561:,
3546:MR
3544:,
3536:,
3521:MR
3519:,
3511:,
3486:MR
3484:.
3474:.
3451:MR
3449:.
3439:.
3411:.
3399:36
3397:.
3393:.
3361:MR
3348:MR
3342:.
3338:,
3325:.
3229:.
3205:.
3187:.
3063:.
2863:.
2848:.
2763:.
2689:.
2385:.
2345:→
2305:.
2297:→
2253:→
2219:→
2191:,
2183:∊
2150:→
2101:→
2057:⊂
2049:,
2033:,
2002:∊
1974:.
298:.
278:,
209:→
162:∈
154:⊂
143:.
83:.
66:.
4275:2
4273:G
4242:?
4207:p
4192:)
4189:8
4187:E
4182:7
4180:E
4175:6
4173:E
4168:4
4166:F
4161:2
4159:G
4157:(
3753:e
3746:t
3739:v
3725:.
3711::
3676:.
3672::
3646:.
3617:.
3595::
3569:.
3557::
3532::
3507::
3492:.
3457:.
3435::
3419:.
3415::
3278:.
3239:.
3215:.
3191:.
2980:H
2976:n
2972:H
2968:P
2964:g
2960:d
2952:g
2937:G
2933:T
2929:G
2927:/
2925:T
2921:G
2917:G
2905:T
2838:X
2834:X
2824:n
2820:X
2818:(
2815:n
2720:1
2717:,
2714:1
2704:M
2687:n
2683:g
2667:n
2664:,
2661:g
2651:M
2625:n
2622:,
2619:g
2613:M
2600:n
2596:g
2592:n
2588:g
2581:g
2577:g
2561:1
2555:M
2522:0
2516:M
2503:g
2499:g
2495:g
2476:g
2466:M
2452:g
2448:g
2432:g
2426:M
2371:B
2367:B
2359:B
2355:B
2347:X
2343:S
2339:X
2335:L
2331:L
2327:S
2323:L
2319:L
2303:M
2299:M
2295:U
2291:M
2279:M
2275:W
2271:V
2267:M
2263:W
2259:V
2255:M
2251:B
2246:T
2241:B
2237:T
2233:F
2229:M
2225:M
2217:F
2213:F
2205:M
2193:M
2189:M
2187:(
2180:M
2176:1
2172:M
2168:M
2164:M
2156:M
2148:F
2144:F
2138:M
2134:F
2126:M
2122:B
2118:B
2114:F
2107:M
2103:M
2099:B
2095:U
2087:B
2083:T
2071:U
2063:M
2059:V
2055:L
2051:V
2047:k
2045:(
2043:G
2039:k
2035:V
2031:k
2029:(
2027:G
2023:M
2019:U
2010:m
2008:U
2004:M
2000:m
1996:M
1984:M
1962:f
1942:d
1922:)
1919:f
1916:(
1913:V
1890:}
1887:)
1884:)
1881:d
1878:(
1873:O
1868:(
1859:f
1856::
1853:)
1850:f
1847:,
1844:)
1841:f
1838:(
1835:V
1832:(
1829:{
1826:=
1821:U
1793:)
1790:)
1787:)
1784:d
1781:(
1776:O
1771:(
1765:(
1761:P
1757:=
1754:)
1749:n
1744:P
1739:(
1734:d
1728:b
1725:l
1722:i
1719:H
1691:n
1686:P
1664:d
1654:X
1650:X
1648:(
1642:X
1640:(
1623:P
1615:d
1611:d
1606:C
1604:D
1600:C
1596:C
1592:P
1588:G
1583:C
1581:D
1575:d
1571:C
1567:P
1563:P
1559:d
1555:C
1551:P
1547:d
1543:P
1514:1
1511:+
1508:n
1488:X
1480:L
1456:n
1452:x
1442:i
1438:,
1432:,
1427:0
1423:x
1413:i
1392:)
1389:1
1386:(
1379:n
1373:Z
1367:P
1359:O
1347:i
1324:n
1318:Z
1312:P
1304:X
1301::
1298:i
1271:/
1266:}
1249:)
1244:L
1239:,
1236:X
1233:(
1222:n
1218:s
1214:,
1208:,
1203:0
1199:s
1186:X
1178:L
1169::
1166:)
1161:n
1157:s
1153:,
1147:,
1142:0
1138:s
1134:,
1129:L
1124:(
1120:{
1116:=
1113:)
1110:X
1107:(
1102:n
1096:Z
1090:P
1065:X
1029::
1024:n
1018:Z
1012:P
982:i
978:s
974:=
971:)
966:i
962:s
958:(
929:L
918:L
913::
887:)
884:)
876:n
872:s
868:,
862:,
854:0
850:s
846:(
843:,
834:L
828:(
822:)
819:)
814:n
810:s
806:,
800:,
795:0
791:s
787:(
784:,
779:L
774:(
748:)
745:R
742:(
737:n
731:Z
725:P
717:]
714:)
711:x
708:(
703:n
699:s
695::
689::
686:)
683:x
680:(
675:0
671:s
667:[
664:=
661:x
655:]
650:n
646:s
642::
636::
631:0
627:s
623:[
595:n
589:Z
583:P
575:)
572:R
569:(
561::
552:x
523:X
517:)
514:R
511:(
503::
500:x
477:)
472:L
467:,
464:X
461:(
450:n
446:s
442:,
436:,
431:0
427:s
406:1
403:+
400:n
380:X
372:L
348:n
342:Z
336:P
314:X
296:V
292:k
288:F
284:V
280:V
276:k
274:(
272:G
262:C
254:R
250:P
230:R
226:R
224:(
222:P
215:R
213:(
211:P
207:S
196:S
192:R
190:(
188:P
184:s
180:s
176:s
172:s
170:(
168:L
164:S
160:s
156:R
152:S
148:R
137:R
135:(
133:P
129:L
125:L
121:L
117:R
111:.
109:S
105:R
103:(
101:P
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.