553:
148:
564:
form a lattice in which the lattice's partial ordering is given by set inclusion, the join operation corresponds to set union, and the meet operation corresponds to set intersection, because unions and intersections preserve the property of being a lower set. Because set unions and intersections obey
1223:
In an infinite distributive lattice, it may not be the case that the lower sets of the join-irreducible elements are in one-to-one correspondence with lattice elements. Indeed, there may be no join-irreducibles at all. This happens, for instance, in the lattice of all natural numbers, ordered with
282:
Birkhoff's theorem states that this relation between the operations ∧ and ∨ of the lattice of divisors and the operations ∩ and ∪ of the associated sets of prime powers is not coincidental, and not dependent on the specific properties of prime numbers and divisibility: the elements of any finite
1306:
showed that Stone's representation theorem could be interpreted as an extension of the idea of representing lattice elements by lower sets of a partial order, using
Nachbin's idea of ordered topological spaces. Stone spaces with an additional partial order linked with the topology via
246:
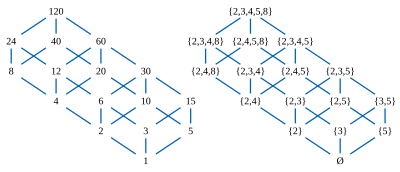
that divide it: thus, 12 is associated with the set {2,3,4}, while 20 is associated with the set {2,4,5}. Then 12 ∧ 20 = 4 is associated with the set {2,3,4} ∩ {2,4,5} = {2,4}, while 12 ∨ 20 = 60 is associated with the set
250:
The prime powers 2, 3, 4, 5, and 8 appearing as elements in these sets may themselves be partially ordered by divisibility; in this smaller partial order, 2 ≤ 4 ≤ 8 and there are no order relations between other pairs. The 16 sets that are associated with divisors of 120 are the
330:
is join-irreducible if it is neither the bottom element of the lattice (the join of zero elements) nor the join of any two smaller elements. For instance, in the lattice of divisors of 120, there is no pair of elements whose join is 4, so 4 is join-irreducible. An element
69:. The union and intersection operations, in a family of sets that is closed under these operations, automatically form a distributive lattice, and Birkhoff's representation theorem states that every finite distributive lattice can be formed in this way. It is named after
127:
Many lattices can be defined in such a way that the elements of the lattice are represented by sets, the join operation of the lattice is represented by set union, and the meet operation of the lattice is represented by set intersection. For instance, the
1490:
809:
Birkhoff's theorem, as stated above, is a correspondence between individual partial orders and distributive lattices. However, it can also be extended to a correspondence between order-preserving functions of partial orders and
1327:
topologies on a set to represent an abstract distributive lattice. Thus, Birkhoff's representation theorem extends to the case of infinite (bounded) distributive lattices in at least three different ways, summed up in
1627:
A minor difference between the 2-SAT and initial stable set formulations is that the latter presupposes the choice of a fixed base point from the median graph that corresponds to the empty initial stable
1531:, one on the positive variables of the instance and the other on the negative variables; the transitive closure of the positive component is the underlying partial order of the distributive lattice.
1210:
between, on the one hand, the category of finite partial orders and order-preserving maps, and on the other hand the category of finite distributive lattices and bounded lattice homomorphisms.
437:
There exist lattices in which the join-prime elements form a proper subset of the join-irreducible elements, but in a distributive lattice the two types of elements coincide. For, suppose that
1346:
167:
12 ∨ 20 = 60; both of these numbers are also divisors of 120. These two operations ∨ and ∧ satisfy the distributive law, in either of two equivalent forms: (
1109:(the meet of all elements mapped to 1), which must be join-irreducible (it cannot be the join of any set of elements mapped to 0), so every lattice homomorphism has the form
1340:
Birkhoff's representation theorem may also be generalized to finite structures other than distributive lattices. In a distributive lattice, the self-dual median operation
556:
Distributive example lattice, with join-irreducible elements a,...,g (shadowed nodes). The lower set a node corresponds to by
Birkhoff's isomorphism is shown in blue.
1832:
1547:, a family of sets closed under unions but in which closure under intersections has been replaced by the property that each nonempty set has a removable element.
144:
finite distributive lattices can be obtained this way, and later generalizations of
Birkhoff's theorem state a similar thing for infinite distributive lattices.
1702:
279:. Thus, the partial order on the five prime powers 2, 3, 4, 5, and 8 carries enough information to recover the entire original 16-element divisibility lattice.
1806:
386:
In any lattice, a join-prime element must be join-irreducible. Equivalently, an element that is not join-irreducible is not join-prime. For, if an element
565:
the distributive law, this is a distributive lattice. Birkhoff's theorem states that any finite distributive lattice can be constructed in this way.
159:
of some composite number, such as (in the figure) 120, partially ordered by divisibility. Any two divisors of 120, such as 12 and 20, have a unique
1329:
247:{2,3,4} ∪ {2,4,5} = {2,3,4,5}, so the join and meet operations of the lattice correspond to union and intersection of sets.
1519:. For a distributive lattice, the corresponding mixed graph has no undirected edges, and the initial stable sets are just the lower sets of the
26:
1791:
100:
1885:
801:. The ring of sets itself is then the family of lower sets of this preorder, and any preorder gives rise to a ring of sets in this way.
1528:
1746:
781:. If the sets in a ring of sets are ordered by inclusion, they form a distributive lattice. The elements of the sets may be given a
1265:
1779:
1539:
Another result analogous to
Birkhoff's representation theorem, but applying to a broader class of lattices, is the theorem of
1644:
1512:
294:-element set, partially ordered by inclusion. Birkhoff's theorem shows this lattice to be produced by the lower sets of the
99:
The name “Birkhoff's representation theorem” has also been applied to two other results of
Birkhoff, one from 1935 on the
65:, the "meet" and "join" operations, which must obey certain axioms; it is distributive if these two operations obey the
1556:
821:
denote the partial order on the two-element set {0, 1}, with the order relation 0 < 1, and (following
Stanley) let
115:
representing algebras as products of irreducible algebras. Birkhoff's representation theorem has also been called the
1672:
1287:
1207:
295:
112:
58:
544:; Birkhoff's theorem states that the lattice itself can be recovered from the lower sets of this partial order.
884:
133:
93:
1485:{\displaystyle m(x,y,z)=(x\vee y)\wedge (x\vee z)\wedge (y\vee z)=(x\wedge y)\vee (x\wedge z)\vee (y\wedge z)}
814:
of the corresponding distributive lattices. The direction of these maps is reversed in this correspondence.
767:
160:
763:
164:
275:, one can recover the associated divisor by computing the least common multiple of the prime powers in
1734:
1320:
811:
236:
46:
576:
is isomorphic to the lattice of lower sets of the partial order of the join-irreducible elements of
140:, any lattice defined in this way is a distributive lattice. Birkhoff's theorem states that in fact
1758:
1316:
552:
1863:
1520:
54:
136:
has a lattice of sets as its family of open sets. Because set unions and intersections obey the
1787:
1742:
1524:
1503:. Finite median algebras and median graphs have a dual structure as the set of solutions of a
1298:), topological spaces in which the compact open sets are closed under intersection and form a
1280:
766:
under the operations of set unions and set intersections; later, motivated by applications in
132:
defined from the family of all subsets of a finite set has this property. More generally any
1870:, Cambridge Studies in Advanced Mathematics 49, Cambridge University Press, pp. 104–112
1849:
1841:
1827:
1815:
1801:
1767:
1711:
1693:
1681:
1667:
1653:
1504:
1303:
163:
12 ∧ 20 = 4, the largest number that divides both of them, and a unique
151:
The distributive lattice of divisors of 120, and its representation as sets of prime powers.
137:
70:
66:
62:
1725:
1264:. However, elements in infinite distributive lattices may still be represented as sets via
283:
distributive lattice may be associated with lower sets of a partial order in the same way.
1721:
1312:
1308:
1299:
1284:
1188:
777:
303:
129:
85:
1496:
1295:
1291:
759:
22:
1830:(1972), "Ordered topological spaces and the representation of distributive lattices",
1311:
can also be used to represent bounded distributive lattices. Such spaces are known as
1879:
1756:
Edelman, Paul H. (1980), "Meet-distributive lattices and the anti-exchange closure",
1658:
1273:
1269:
541:
81:
1804:(1970), "Representation of distributive lattices by means of ordered Stone spaces",
1716:
1642:
Barthélemy, J.-P.; Constantin, J. (1993), "Median graphs, parallelism and posets",
1500:
1261:
584:
That is, there is a one-to-one order-preserving correspondence between elements of
1697:
1685:
731:
is the join of two or more join-irreducible items then they must again belong to
1544:
1516:
1196:
243:
103:
as families of sets closed under union, intersection, and complement (so-called
35:
1845:
588:
and lower sets of the partial order. The lower set corresponding to an element
1854:
50:
43:
561:
252:
77:
1819:
1093:
to 1 and all other lower sets to 0. And, for any lattice homomorphism from
1066:
themselves correspond one-for-one with bounded lattice homomorphisms from
841:. For, if ƒ is such a function, ƒ(0) forms a lower set, and conversely if
1276:
782:
743:. Therefore, the correspondence is one-to-one and the theorem is proved.
635:
be the lower set of the join-irreducible elements less than or equal to
89:
1132:
one may use composition of functions to define an order-preserving map
825:
denote the distributive lattice of lower sets of a finite partial order
659:
must (by join-primality) be less than or equal to one of the members of
540:
The lattice ordering on the subset of join-irreducible elements forms a
493:
is join-irreducible, at least one of the two terms in this join must be
147:
1771:
156:
287:
1543:
that any finite join-distributive lattice may be represented as an
551:
146:
326:
is not the join of a finite set of other elements. Equivalently,
1283:. This generalized representation theorem can be expressed as a
255:
of this smaller partial order, subsets of elements such that if
1511:
formulate this structure equivalently as the family of initial
833:
correspond one-for-one to the order-preserving functions from
1527:
of the 2-satisfiability instance can be partitioned into two
991:
if and only if belongs both to the set of elements mapped to
1523:
of the graph. Equivalently, for a distributive lattice, the
845:
is a lower set one may define an order-preserving function ƒ
302:
generators, the number of elements of which is given by the
1294:(sometimes called coherent spaces, but not the same as the
61:
of sets. Here, a lattice is an abstract structure with two
111:
used by
Birkhoff to represent distributive lattices), and
53:, in such a way that the lattice operations correspond to
42:
for distributive lattices states that the elements of any
655:, and any join-irreducible element less than or equal to
1105:
that are mapped to 1 must have a unique minimal element
683:
be the join-irreducible elements less than or equal to
453:. This inequality is equivalent to the statement that
1559:, also representing every finite distributive lattice
1349:
367:. In the same lattice, 4 is join-prime: whenever lcm(
339:
if it differs from the bottom element, and whenever
16:
Equivalence of distributive lattices and set families
1508:
1323:, generalize Stone's original approach by utilizing
117:
fundamental theorem for finite distributive lattices
1499:, and the covering relation of the lattice forms a
1224:the reverse of the usual divisibility ordering (so
703:. For, as a join of elements less than or equal to
271:must also belong to the subset. From any lower set
1484:
596:is simply the set of join-irreducible elements of
1082:, one may define a bounded lattice homomorphism
1272:in which each lattice element corresponds to a
1120:. Again, from any bounded lattice homomorphism
771:
242:One may associate each divisor with the set of
1833:Proceedings of the London Mathematical Society
1786:, Cambridge University Press, pp. 62–69,
1698:"A ternary operation in distributive lattices"
1535:Finite join-distributive lattices and matroids
76:The theorem can be interpreted as providing a
1703:Bulletin of the American Mathematical Society
855:to 0 and that maps the remaining elements of
663:, and therefore must (by the assumption that
390:is not join-irreducible, there exist smaller
8:
1615:
612:of join-irreducible elements is the join of
286:As another example, consider the lattice of
1807:Bulletin of the London Mathematical Society
1853:
1715:
1657:
1603:
1587:
1585:
1348:
1059:* is a homomorphism of bounded lattices.
25:. For other similarly named results, see
1576:
1330:duality theory for distributive lattices
1244:can be expressed as the join of numbers
1031:(the function that maps all elements of
913:and therefore corresponds to an element
751:
235:. Therefore, the divisors form a finite
1591:
1569:
1540:
1027:). Additionally, the bottom element of
793:whenever some set in the ring contains
73:, who published a proof of it in 1937.
863:is any order-preserving function from
310:The partial order of join-irreducibles
1268:for distributive lattices, a form of
1172:for any bounded lattice homomorphism
434:, showing that it is not join-prime.
375:) is divisible by 4, at least one of
7:
1089:that maps all lower sets containing
671:itself. Conversely, for any element
426:is not less than or equal to either
1868:Enumerative Combinatorics, Volume I
27:Birkhoff's theorem (disambiguation)
1509:Barthélemy & Constantin (1993)
1336:Median algebras and related graphs
1290:between distributive lattices and
995:and the set of elements mapped to
623:of join-irreducible elements, let
572:. Any finite distributive lattice
101:representation of Boolean algebras
80:between distributive lattices and
14:
1782:(1982), "II.3 Coherent locales",
40:Birkhoff's representation theorem
1717:10.1090/S0002-9904-1947-08864-9
1296:coherent spaces in linear logic
905:. This composite function maps
600:that are less than or equal to
469:), and by the distributive law
383:must itself be divisible by 4.
1479:
1467:
1461:
1449:
1443:
1431:
1425:
1413:
1407:
1395:
1389:
1377:
1371:
1353:
1266:Stone's representation theorem
1219:Infinite distributive lattices
441:is join-irreducible, and that
86:quasi-ordinal knowledge spaces
1:
1686:10.1215/S0012-7094-37-00334-X
1152:for any order-preserving map
772:Doignon & Falmagne (1999)
608:corresponding to a lower set
1659:10.1016/0012-365X(93)90140-O
871:, one may define a function
774:called the same structure a
497:itself, showing that either
267:belongs to the subset, then
1557:Lattice of stable matchings
1039:* to the bottom element of
747:Rings of sets and preorders
1902:
1886:Theorems in lattice theory
1616:Birkhoff & Kiss (1947)
1309:Priestley separation axiom
1144:. It may be verified that
667:is a lower set) belong to
560:In any partial order, the
1673:Duke Mathematical Journal
1670:(1937), "Rings of sets",
1197:contravariant hom-functor
1062:However, the elements of
1043:, and the top element of
719:is join-irreducible then
314:In a lattice, an element
296:free distributive lattice
107:, closely related to the
94:finite topological spaces
78:one-to-one correspondence
1846:10.1112/plms/s3-24.3.507
1051:* to the top element of
885:composition of functions
647:. For, every element of
134:finite topological space
829:. Then the elements of
768:mathematical psychology
711:can be no greater than
547:
123:Background and examples
1696:; Kiss, S. A. (1947),
1486:
557:
161:greatest common factor
152:
113:Birkhoff's HSP theorem
49:can be represented as
1487:
1321:pairwise Stone spaces
1208:duality of categories
812:bounded homomorphisms
604:, and the element of
555:
165:least common multiple
150:
1820:10.1112/blms/2.2.186
1645:Discrete Mathematics
1529:connected components
1347:
1317:bitopological spaces
999:) and symmetrically
237:distributive lattice
47:distributive lattice
1759:Algebra Universalis
1741:, Springer-Verlag,
1315:. Further, certain
1202: = Hom(—,
1035:to 0) is mapped by
935:. Further, for any
887:to map any element
651:clearly belongs to
1855:10338.dmlcz/134149
1772:10.1007/BF02482912
1521:transitive closure
1482:
1302:for the topology.
1285:category-theoretic
1189:category theoretic
1101:, the elements of
1078:is any element of
619:For any lower set
558:
548:Birkhoff's theorem
153:
1793:978-0-521-33779-3
1694:Birkhoff, Garrett
1668:Birkhoff, Garrett
1525:implication graph
1281:topological space
1206:) that defines a
983:to the lower set
975:) (an element of
63:binary operations
1893:
1871:
1858:
1857:
1828:Priestley, H. A.
1822:
1802:Priestley, H. A.
1796:
1780:Johnstone, Peter
1774:
1751:
1739:Knowledge Spaces
1735:Falmagne, J.-Cl.
1733:Doignon, J.-P.;
1728:
1719:
1688:
1662:
1661:
1629:
1625:
1619:
1613:
1607:
1604:Johnstone (1982)
1601:
1595:
1589:
1580:
1574:
1505:2-satisfiability
1495:gives rise to a
1491:
1489:
1488:
1483:
1313:Priestley spaces
1304:Hilary Priestley
921:) = (ƒ
320:join-irreducible
304:Dedekind numbers
138:distributive law
71:Garrett Birkhoff
67:distributive law
1901:
1900:
1896:
1895:
1894:
1892:
1891:
1890:
1876:
1875:
1862:
1826:
1800:
1794:
1778:
1755:
1749:
1732:
1692:
1666:
1641:
1638:
1633:
1632:
1626:
1622:
1614:
1610:
1602:
1598:
1590:
1583:
1577:Birkhoff (1937)
1575:
1571:
1566:
1553:
1537:
1345:
1344:
1338:
1292:spectral spaces
1221:
1216:
1214:Generalizations
1168:** =
1148:** =
1114:
1087:
926:
900:
850:
807:
778:knowledge space
752:Birkhoff (1937)
749:
715:itself, but if
691:be the join of
627:be the join of
550:
481:) ∨ (
312:
215:) ∨ (
187:) ∧ (
130:Boolean lattice
125:
96:and preorders.
17:
12:
11:
5:
1899:
1897:
1889:
1888:
1878:
1877:
1874:
1873:
1864:Stanley, R. P.
1860:
1840:(3): 507–530,
1824:
1814:(2): 186–190,
1798:
1792:
1776:
1766:(1): 290–299,
1753:
1747:
1730:
1710:(1): 749–752,
1690:
1680:(3): 443–454,
1664:
1652:(1–3): 49–63,
1637:
1634:
1631:
1630:
1620:
1608:
1596:
1592:Stanley (1997)
1581:
1568:
1567:
1565:
1562:
1561:
1560:
1552:
1549:
1541:Edelman (1980)
1536:
1533:
1497:median algebra
1493:
1492:
1481:
1478:
1475:
1472:
1469:
1466:
1463:
1460:
1457:
1454:
1451:
1448:
1445:
1442:
1439:
1436:
1433:
1430:
1427:
1424:
1421:
1418:
1415:
1412:
1409:
1406:
1403:
1400:
1397:
1394:
1391:
1388:
1385:
1382:
1379:
1376:
1373:
1370:
1367:
1364:
1361:
1358:
1355:
1352:
1337:
1334:
1240:): any number
1220:
1217:
1215:
1212:
1112:
1085:
1019:) ∨
1011:) =
967:) ∧
959:) =
922:
896:
883:that uses the
846:
806:
803:
776:quasi-ordinal
760:family of sets
748:
745:
582:
581:
549:
546:
529:(equivalently
509:(equivalently
473: = (
461: ∧ (
311:
308:
207: = (
203:) ∧
179: = (
175:) ∨
124:
121:
105:fields of sets
82:partial orders
32:
31:
23:lattice theory
21:This is about
15:
13:
10:
9:
6:
4:
3:
2:
1898:
1887:
1884:
1883:
1881:
1869:
1865:
1861:
1856:
1851:
1847:
1843:
1839:
1835:
1834:
1829:
1825:
1821:
1817:
1813:
1809:
1808:
1803:
1799:
1795:
1789:
1785:
1781:
1777:
1773:
1769:
1765:
1761:
1760:
1754:
1750:
1748:3-540-64501-2
1744:
1740:
1736:
1731:
1727:
1723:
1718:
1713:
1709:
1705:
1704:
1699:
1695:
1691:
1687:
1683:
1679:
1675:
1674:
1669:
1665:
1660:
1655:
1651:
1647:
1646:
1640:
1639:
1635:
1624:
1621:
1617:
1612:
1609:
1605:
1600:
1597:
1593:
1588:
1586:
1582:
1578:
1573:
1570:
1563:
1558:
1555:
1554:
1550:
1548:
1546:
1542:
1534:
1532:
1530:
1526:
1522:
1518:
1514:
1510:
1506:
1502:
1498:
1476:
1473:
1470:
1464:
1458:
1455:
1452:
1446:
1440:
1437:
1434:
1428:
1422:
1419:
1416:
1410:
1404:
1401:
1398:
1392:
1386:
1383:
1380:
1374:
1368:
1365:
1362:
1359:
1356:
1350:
1343:
1342:
1341:
1335:
1333:
1331:
1326:
1322:
1318:
1314:
1310:
1305:
1301:
1297:
1293:
1289:
1286:
1282:
1279:in a certain
1278:
1275:
1271:
1270:Stone duality
1267:
1263:
1262:prime numbers
1260:are distinct
1259:
1255:
1251:
1247:
1243:
1239:
1235:
1231:
1228: ≤
1227:
1218:
1213:
1211:
1209:
1205:
1201:
1198:
1194:
1191:terminology,
1190:
1185:
1183:
1179:
1175:
1171:
1167:
1164:and that and
1163:
1159:
1155:
1151:
1147:
1143:
1139:
1135:
1131:
1127:
1123:
1119:
1115:
1108:
1104:
1100:
1096:
1092:
1088:
1081:
1077:
1073:
1069:
1065:
1060:
1058:
1054:
1050:
1047:is mapped by
1046:
1042:
1038:
1034:
1030:
1026:
1022:
1018:
1014:
1010:
1007: ∨
1006:
1002:
998:
994:
990:
987: ∩
986:
982:
979:is mapped by
978:
974:
970:
966:
962:
958:
955: ∧
954:
950:
946:
942:
938:
934:
930:
927: ∘
925:
920:
916:
912:
908:
904:
901: ∘
899:
894:
890:
886:
882:
878:
874:
870:
866:
862:
858:
854:
849:
844:
840:
836:
832:
828:
824:
820:
815:
813:
805:Functoriality
804:
802:
800:
796:
792:
789: ≤
788:
784:
780:
779:
773:
769:
765:
761:
757:
753:
746:
744:
742:
739: ≥
738:
734:
730:
726:
722:
718:
714:
710:
706:
702:
699: =
698:
694:
690:
686:
682:
678:
674:
670:
666:
662:
658:
654:
650:
646:
643: =
642:
638:
634:
630:
626:
622:
617:
615:
611:
607:
603:
599:
595:
591:
587:
579:
575:
571:
568:
567:
566:
563:
554:
545:
543:
542:partial order
538:
536:
533: ≤
532:
528:
525: ∧
524:
521: =
520:
516:
513: ≤
512:
508:
505: ∧
504:
501: =
500:
496:
492:
489:). But since
488:
485: ∧
484:
480:
477: ∧
476:
472:
468:
465: ∨
464:
460:
457: =
456:
452:
449: ∨
448:
445: ≤
444:
440:
435:
433:
429:
425:
421:
418: ∨
417:
414: ≤
413:
409:
406: ∨
405:
402: =
401:
397:
393:
389:
384:
382:
378:
374:
370:
366:
363: ≤
362:
358:
355: ≤
354:
350:
347: ∨
346:
343: ≤
342:
338:
334:
329:
325:
321:
317:
309:
307:
305:
301:
297:
293:
289:
284:
280:
278:
274:
270:
266:
262:
258:
254:
248:
245:
240:
238:
234:
230:
226:
222:
219: ∧
218:
214:
211: ∧
210:
206:
202:
199: ∨
198:
194:
191: ∨
190:
186:
183: ∨
182:
178:
174:
171: ∧
170:
166:
162:
158:
155:Consider the
149:
145:
143:
139:
135:
131:
122:
120:
118:
114:
110:
109:rings of sets
106:
102:
97:
95:
92:, or between
91:
87:
83:
79:
74:
72:
68:
64:
60:
59:intersections
56:
52:
48:
45:
41:
37:
30:
28:
24:
19:
18:
1867:
1837:
1831:
1811:
1805:
1784:Stone Spaces
1783:
1763:
1757:
1738:
1707:
1701:
1677:
1671:
1649:
1643:
1623:
1611:
1599:
1572:
1538:
1501:median graph
1494:
1339:
1324:
1257:
1253:
1249:
1245:
1241:
1237:
1233:
1229:
1225:
1222:
1203:
1199:
1192:
1186:
1181:
1177:
1173:
1169:
1165:
1161:
1157:
1153:
1149:
1145:
1141:
1137:
1133:
1129:
1125:
1121:
1117:
1110:
1106:
1102:
1098:
1094:
1090:
1083:
1079:
1075:
1071:
1067:
1063:
1061:
1056:
1052:
1048:
1044:
1040:
1036:
1032:
1028:
1024:
1020:
1016:
1012:
1008:
1004:
1000:
996:
992:
988:
984:
980:
976:
972:
968:
964:
960:
956:
952:
948:
944:
940:
936:
932:
928:
923:
918:
914:
910:
906:
902:
897:
892:
888:
880:
876:
872:
868:
864:
860:
856:
852:
847:
842:
838:
834:
830:
826:
822:
818:
816:
808:
798:
794:
790:
786:
775:
756:ring of sets
755:
750:
740:
736:
732:
728:
724:
720:
716:
712:
708:
704:
700:
696:
692:
688:
684:
680:
676:
672:
668:
664:
660:
656:
652:
648:
644:
640:
636:
632:
628:
624:
620:
618:
613:
609:
605:
601:
597:
593:
589:
585:
583:
577:
573:
569:
559:
539:
534:
530:
526:
522:
518:
514:
510:
506:
502:
498:
494:
490:
486:
482:
478:
474:
470:
466:
462:
458:
454:
450:
446:
442:
438:
436:
431:
427:
423:
419:
415:
411:
407:
403:
399:
395:
391:
387:
385:
380:
376:
372:
368:
364:
360:
356:
352:
348:
344:
340:
336:
332:
327:
323:
319:
315:
313:
299:
291:
285:
281:
276:
272:
268:
264:
260:
256:
249:
244:prime powers
241:
232:
228:
224:
220:
216:
212:
208:
204:
200:
196:
192:
188:
184:
180:
176:
172:
168:
154:
141:
126:
116:
108:
104:
98:
75:
39:
33:
20:
1545:antimatroid
1517:mixed graph
1513:stable sets
1055:. That is,
723:belongs to
410:. But then
223:), for all
51:finite sets
36:mathematics
1636:References
1507:instance;
1074:. For, if
851:that maps
754:defined a
687:, and let
631:, and let
562:lower sets
398:such that
337:join-prime
253:lower sets
84:, between
1474:∧
1465:∨
1456:∧
1447:∨
1438:∧
1420:∨
1411:∧
1402:∨
1393:∧
1384:∨
1319:, namely
1116:for some
859:to 1. If
785:in which
727:while if
351:, either
90:preorders
1880:Category
1866:(1997),
1737:(1999),
1551:See also
1277:open set
1236:divides
931:)(0) of
797:but not
783:preorder
762:that is
758:to be a
157:divisors
1726:0021540
1288:duality
1274:compact
1136:* from
875:* from
695:. Then
639:. Then
570:Theorem
288:subsets
195:) and (
1790:
1745:
1724:
1252:where
764:closed
679:, let
422:, and
290:of an
231:, and
55:unions
44:finite
1564:Notes
1515:in a
1232:when
1195:is a
1176:from
1156:from
1124:from
895:to ƒ
735:, so
517:) or
1788:ISBN
1743:ISBN
1628:set.
1300:base
1256:and
1248:and
1182:J(Q)
1178:J(P)
1130:J(Q)
1126:J(P)
1103:J(P)
1095:J(P)
1068:J(P)
1053:J(Q)
1045:J(P)
1041:J(Q)
1029:J(P)
945:J(P)
939:and
933:J(Q)
893:J(P)
881:J(Q)
877:J(P)
831:J(P)
823:J(P)
817:Let
394:and
379:and
263:and
88:and
57:and
1850:hdl
1842:doi
1816:doi
1768:doi
1712:doi
1682:doi
1654:doi
1650:111
1325:two
1187:In
1180:to
1160:to
1140:to
1128:to
1097:to
1070:to
943:in
909:to
891:of
879:to
867:to
837:to
675:of
592:of
537:).
430:or
359:or
335:is
322:if
318:is
298:on
142:all
34:In
1882::
1848:,
1838:24
1836:,
1810:,
1764:10
1762:,
1722:MR
1720:,
1708:53
1706:,
1700:,
1676:,
1648:,
1584:^
1332:.
1250:xq
1246:xp
1184:.
1023:*(
1015:*(
1003:*(
971:*(
963:*(
951:*(
947:,
917:*(
770:,
707:,
616:.
306:.
259:≤
239:.
227:,
119:.
38:,
1872:.
1859:.
1852::
1844::
1823:.
1818::
1812:2
1797:.
1775:.
1770::
1752:.
1729:.
1714::
1689:.
1684::
1678:3
1663:.
1656::
1618:.
1606:.
1594:.
1579:.
1480:)
1477:z
1471:y
1468:(
1462:)
1459:z
1453:x
1450:(
1444:)
1441:y
1435:x
1432:(
1429:=
1426:)
1423:z
1417:y
1414:(
1408:)
1405:z
1399:x
1396:(
1390:)
1387:y
1381:x
1378:(
1375:=
1372:)
1369:z
1366:,
1363:y
1360:,
1357:x
1354:(
1351:m
1258:q
1254:p
1242:x
1238:x
1234:y
1230:y
1226:x
1204:2
1200:J
1193:J
1174:h
1170:h
1166:h
1162:P
1158:Q
1154:g
1150:g
1146:g
1142:P
1138:Q
1134:h
1122:h
1118:x
1113:x
1111:j
1107:x
1099:2
1091:x
1086:x
1084:j
1080:P
1076:x
1072:2
1064:P
1057:g
1049:g
1037:g
1033:P
1025:y
1021:g
1017:x
1013:g
1009:y
1005:x
1001:g
997:y
993:x
989:y
985:x
981:g
977:Q
973:y
969:g
965:x
961:g
957:y
953:x
949:g
941:y
937:x
929:g
924:L
919:L
915:g
911:2
907:Q
903:g
898:L
889:L
873:g
869:P
865:Q
861:g
857:P
853:L
848:L
843:L
839:2
835:P
827:P
819:2
799:y
795:x
791:y
787:x
741:x
737:y
733:S
729:x
725:S
721:x
717:x
713:x
709:y
705:x
701:y
697:x
693:S
689:y
685:x
681:S
677:L
673:x
669:S
665:S
661:S
657:x
653:T
649:S
645:T
641:S
637:x
633:T
629:S
625:x
621:S
614:S
610:S
606:L
602:x
598:L
594:L
590:x
586:L
580:.
578:L
574:L
535:z
531:x
527:z
523:x
519:x
515:y
511:x
507:y
503:x
499:x
495:x
491:x
487:z
483:x
479:y
475:x
471:x
467:z
463:y
459:x
455:x
451:z
447:y
443:x
439:x
432:z
428:y
424:x
420:z
416:y
412:x
408:z
404:y
400:x
396:z
392:y
388:x
381:z
377:y
373:z
371:,
369:y
365:z
361:x
357:y
353:x
349:z
345:y
341:x
333:x
328:x
324:x
316:x
300:n
292:n
277:L
273:L
269:x
265:y
261:y
257:x
233:z
229:y
225:x
221:z
217:y
213:z
209:x
205:z
201:y
197:x
193:z
189:y
185:z
181:x
177:z
173:y
169:x
29:.
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.