240:
248:
232:
310:. The evolute will have a cusp at the center of the circle. The sign of the second derivative of curvature determines whether the curve has a local minimum or maximum of curvature. All closed curves will have at least four vertices, two minima and two maxima (the
321:
in a 1-parameter family of curves, at a curve in the family where (as the parameter varies) two vertices (one maximum and one minimum) come together and annihilate. At such points the second derivative of curvature will be zero.
103:
from a given family of curves is a curve that has the highest possible order of contact with a given curve at a given point; for instance a
435:
411:
387:
451:
456:
461:
428:
466:
143:
135:
42:
31:
317:
In general a curve will not have 4th-order contact with any circle. However, 4th-order contact can occur
107:
is an osculating curve from the family of lines, and has first-order contact with the given curve; an
65:
311:
292:
139:
77:
306:) is zero, then the osculating circle will have 3rd-order contact and the curve is said to have a
150:
431:
407:
383:
377:
272:
127:
108:
69:
288:
131:
100:
420:
264:
295:
of the centers of all the osculating circles (also called "centers of curvature") is the
307:
445:
318:
352:
123:
104:
17:
356:
239:
73:
38:
61:
247:
213:
231:
99:. (Here the derivatives are considered with respect to arc length.) An
115:, and has second-order contact (same tangent angle and curvature), etc.
296:
222:
4th-order contact if the second derivatives of the curvature are equal.
206:
179:
96:
30:
This article is about contact of functions. For contact relations, see
76:. Contact is a geometric notion; it can be defined algebraically as a
202:
0th-order contact if the curves have a simple crossing (not tangent).
112:
246:
238:
230:
84:
27:
Two functions having equal values and derivatives at a given point
186:-series where there is a high degree of contact with the sphere.
219:
3rd-order contact if the derivatives of the curvature are equal.
216:
of the curves are equal. Such curves are said to be osculating.
153:, where the type of contact are classified, these include the
291:
on the curve), the osculating circle is a straight line. The
351:
circles. The centers of all bi-tangent circles form the
325:
Ccircles which have two-point contact with two points
251:
A circle with 3rd-order contact at a vertex of a curve
138:
are related changes of coordinates, of importance in
95:(i.e. kissing), generalising the property of being
91:-th order contact at a point: this is also called
68:, whose equivalence classes are generally called
194:Two curves in the plane intersecting at a point
149:Contact between manifolds is often studied in
130:of degree 1 on odd-dimensional manifolds; see
72:. The point of osculation is also called the
8:
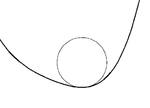
243:A circle with 2nd-order contact (osculating)
57:, they have the same value and their first
111:is an osculating curve from the family of
235:A circle with 1st-order contact (tangent)
205:1st-order contact if the two curves are
368:
275:, whose radius is the reciprocal of κ(
32:heterogeneous relation § Contact
7:
227:Contact between a curve and a circle
402:Bruce, J. W.; P.J. Giblin (1992).
302:If the derivative of curvature κ'(
287:. Where curvature is zero (at an
25:
359:is a subset of the symmetry set.
382:, CRC Press, pp. 174–175,
1:
87:and geometric objects having
178:: osculating, ...) and the
483:
429:Cambridge University Press
29:
425:Geometric Differentiation
212:2nd-order contact if the
404:Curves and Singularities
271:, there is exactly one
144:Legendre transformation
136:Contact transformations
64:are equal. This is an
452:Multivariable calculus
376:Rutter, J. W. (2000),
252:
244:
236:
190:Contact between curves
457:Differential geometry
250:
242:
234:
279:), the curvature of
66:equivalence relation
312:four-vertex theorem
140:classical mechanics
83:One speaks also of
462:Singularity theory
427:, pp 152–7,
379:Geometry of Curves
253:
245:
237:
198:are said to have:
151:singularity theory
128:differential forms
18:Contact (geometry)
347:) on a curve are
273:osculating circle
109:osculating circle
16:(Redirected from
474:
467:Contact geometry
417:
394:
392:
373:
289:inflection point
132:contact geometry
101:osculating curve
90:
60:
56:
52:
21:
482:
481:
477:
476:
475:
473:
472:
471:
442:
441:
421:Ian R. Porteous
414:
401:
398:
397:
390:
375:
374:
370:
365:
346:
335:
255:For each point
229:
192:
177:
170:
163:
126:are particular
121:
88:
58:
54:
53:if, at a point
50:
35:
28:
23:
22:
15:
12:
11:
5:
480:
478:
470:
469:
464:
459:
454:
444:
443:
440:
439:
418:
412:
396:
395:
388:
367:
366:
364:
361:
344:
333:
299:of the curve.
228:
225:
224:
223:
220:
217:
210:
203:
191:
188:
175:
168:
161:
120:
117:
26:
24:
14:
13:
10:
9:
6:
4:
3:
2:
479:
468:
465:
463:
460:
458:
455:
453:
450:
449:
447:
437:
436:0-521-00264-8
433:
430:
426:
422:
419:
415:
413:0-521-42999-4
409:
406:. Cambridge.
405:
400:
399:
391:
389:9781584881667
385:
381:
380:
372:
369:
362:
360:
358:
354:
350:
343:
339:
332:
328:
323:
320:
315:
313:
309:
305:
300:
298:
294:
290:
286:
282:
278:
274:
270:
266:
262:
258:
249:
241:
233:
226:
221:
218:
215:
211:
208:
204:
201:
200:
199:
197:
189:
187:
185:
181:
174:
167:
160:
156:
152:
147:
145:
141:
137:
133:
129:
125:
124:Contact forms
118:
116:
114:
110:
106:
102:
98:
94:
86:
81:
79:
75:
71:
67:
63:
48:
44:
40:
33:
19:
424:
403:
378:
371:
353:symmetry set
348:
341:
337:
330:
326:
324:
316:
303:
301:
284:
280:
276:
268:
267:plane curve
260:
256:
254:
195:
193:
183:
172:
165:
164:: crossing,
158:
154:
148:
122:
119:Applications
105:tangent line
92:
82:
46:
36:
357:medial axis
319:generically
171:: tangent,
142:. See also
74:double cusp
62:derivatives
39:mathematics
446:Categories
363:References
349:bi-tangent
214:curvatures
93:osculation
78:valuation
49:of order
43:functions
157:series (
423:(2001)
297:evolute
263:) on a
207:tangent
180:umbilic
113:circles
97:tangent
47:contact
45:have a
434:
410:
386:
355:. The
308:vertex
265:smooth
85:curves
41:, two
293:locus
432:ISBN
408:ISBN
384:ISBN
70:jets
336:),
314:).
283:at
182:or
37:In
448::
146:.
134:.
80:.
438:.
416:.
393:.
345:2
342:t
340:(
338:S
334:1
331:t
329:(
327:S
304:t
285:t
281:S
277:t
269:S
261:t
259:(
257:S
209:.
196:p
184:D
176:2
173:A
169:1
166:A
162:0
159:A
155:A
89:k
59:k
55:P
51:k
34:.
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.