17:
71:
More generally, every planar graph of minimum degree at least three either has an edge of total degree at most 12, or at least 60 edges that (like the edges in the triakis icosahedron) connect vertices of degrees 3 and 10. If all triangular faces of a polyhedron are vertex-disjoint, there exists an
168:
have edges with unbounded total degree. However, for planar graphs with vertices of degree lower than three, variants of the theorem have been proven, showing that either there is an edge of bounded total degree or some other special kind of subgraph.
166:
127:
427:
326:
372:
Cole, Richard; Kowalik, Łukasz; Škrekovski, Riste (2007), "A generalization of Kotzig's theorem and its application",
64:
has two adjacent faces with a total of at most 13 sides. It was named and popularized in the west in the 1970s by
88:
33:
256:
Borodin, O. V. (1990), "A generalization of Kotzig's theorem and prescribed edge coloring of planar graphs",
298:
Borodin, Oleg V. (1992), "An extension of Kotzig's theorem on the minimum weight of edges in 3-polytopes",
422:
381:
45:
386:
77:
49:
21:
281:
72:
edge with smaller total degree, at most eight. Generalizations of the theorem are also known for
65:
132:
93:
61:
391:
345:
335:
265:
41:
403:
359:
311:
277:
243:
221:
199:
399:
355:
307:
273:
239:
217:
195:
73:
57:
234:
Grünbaum, Branko (1976), "New views on some old questions of combinatorial geometry",
416:
285:
84:
53:
29:
16:
350:
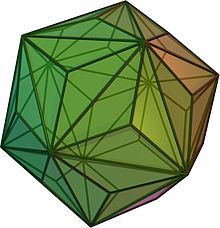
24:, a polyhedron in which every edge has endpoints with total degree at least 13
186:
Kotzig, Anton (1955), "Contribution to the theory of
Eulerian polyhedra",
340:
269:
236:
Colloquio
Internazionale sulle Teorie Combinatorie (Rome, 1973), Tomo I
395:
52:, where no edge has smaller total degree. The result is named after
15:
216:, MAA Studies in Mathematics, vol. 12, pp. 201–224,
238:, Atti dei Convegni Lincei, vol. 17, pp. 451–468,
135:
96:
324:Zaks, Joseph (1983), "Extending Kotzig's theorem",
160:
121:
212:Grünbaum, Branko (1975), "Polytopal graphs",
8:
44:has an edge whose two endpoints have total
385:
349:
339:
140:
134:
101:
95:
83:The theorem cannot be generalized to all
178:
7:
374:SIAM Journal on Discrete Mathematics
48:at most 13. An extreme case is the
56:, who published it in 1955 in the
14:
214:Studies in graph theory, Part II
1:
327:Israel Journal of Mathematics
188:Matematicko-Fyzikálny Časopis
40:is the statement that every
444:
76:onto surfaces with higher
161:{\displaystyle K_{2,n-2}}
122:{\displaystyle K_{1,n-1}}
89:complete bipartite graphs
428:Theorems in graph theory
36:, areas of mathematics,
34:polyhedral combinatorics
258:Matematicheskie Zametki
162:
123:
25:
163:
124:
19:
133:
94:
300:Mathematica Slovaca
50:triakis icosahedron
22:triakis icosahedron
351:10338.dmlcz/127504
341:10.1007/BF02804013
270:10.1007/BF01240258
158:
119:
26:
396:10.1137/050646196
264:(6): 22–28, 160,
62:convex polyhedron
435:
407:
406:
389:
369:
363:
362:
353:
343:
321:
315:
314:
295:
289:
288:
253:
247:
246:
231:
225:
224:
209:
203:
202:
183:
167:
165:
164:
159:
157:
156:
128:
126:
125:
120:
118:
117:
74:graph embeddings
60:form that every
42:polyhedral graph
38:Kotzig's theorem
443:
442:
438:
437:
436:
434:
433:
432:
413:
412:
411:
410:
387:10.1.1.227.3878
371:
370:
366:
323:
322:
318:
297:
296:
292:
255:
254:
250:
233:
232:
228:
211:
210:
206:
185:
184:
180:
175:
136:
131:
130:
97:
92:
91:
66:Branko Grünbaum
12:
11:
5:
441:
439:
431:
430:
425:
415:
414:
409:
408:
364:
334:(4): 281–296,
316:
306:(4): 385–389,
290:
248:
226:
204:
177:
176:
174:
171:
155:
152:
149:
146:
143:
139:
116:
113:
110:
107:
104:
100:
13:
10:
9:
6:
4:
3:
2:
440:
429:
426:
424:
423:Planar graphs
421:
420:
418:
405:
401:
397:
393:
388:
383:
380:(1): 93–106,
379:
375:
368:
365:
361:
357:
352:
347:
342:
337:
333:
329:
328:
320:
317:
313:
309:
305:
301:
294:
291:
287:
283:
279:
275:
271:
267:
263:
259:
252:
249:
245:
241:
237:
230:
227:
223:
219:
215:
208:
205:
201:
197:
193:
189:
182:
179:
172:
170:
153:
150:
147:
144:
141:
137:
114:
111:
108:
105:
102:
98:
90:
86:
85:planar graphs
81:
79:
75:
69:
67:
63:
59:
55:
51:
47:
43:
39:
35:
31:
23:
18:
377:
373:
367:
331:
325:
319:
303:
299:
293:
261:
257:
251:
235:
229:
213:
207:
191:
187:
181:
82:
70:
54:Anton Kotzig
37:
30:graph theory
27:
194:: 101–113,
417:Categories
173:References
382:CiteSeerX
286:120940639
151:−
112:−
87:, as the
404:2299697
360:0720304
312:1195032
278:1102617
244:0470861
222:0406868
200:0074837
402:
384:
358:
310:
284:
276:
242:
220:
198:
46:degree
282:S2CID
78:genus
129:and
58:dual
32:and
20:The
392:doi
346:hdl
336:doi
266:doi
28:In
419::
400:MR
398:,
390:,
378:21
376:,
356:MR
354:,
344:,
332:45
330:,
308:MR
304:42
302:,
280:,
274:MR
272:,
262:48
260:,
240:MR
218:MR
196:MR
190:,
80:.
68:.
394::
348::
338::
268::
192:5
154:2
148:n
145:,
142:2
138:K
115:1
109:n
106:,
103:1
99:K
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.