132:
another segment is drawn upwards by the magnitude of the second coefficient, then left by the magnitude of the third, and down by the magnitude of the fourth, and so on. The sequence of directions (not turns) is always rightward, upward, leftward, downward, then repeating itself. Thus, each turn is counterclockwise. The process continues for every coefficient of the polynomial, including zeros, with negative coefficients "walking backwards." The final point reached, at the end of the segment corresponding to the equation's constant term, is the terminus.
589:
642:
20:
98:
131:
To employ the method, a diagram is drawn starting at the origin. A line segment is drawn rightwards by the magnitude of the first coefficient (the coefficient of the highest-power term) (so that with a negative coefficient, the segment will end left of the origin). From the end of the first segment,
672:
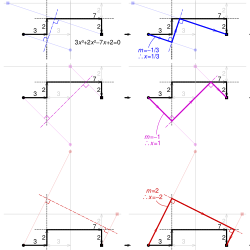
For each root, the paper is folded until the start point (black circle) and end point (black square) are reflected onto these lines. The axis of reflection (dash-dot line) defines the angled path corresponding to the root (blue, purple and red). The negative of the gradients of their first segments,
143:
at a right angle through the line through each segment (including a line for the zero coefficients) when the angled path does not hit the line segment on that line. The vertical and horizontal lines are reflected off or refracted through in the following sequence: the line containing the segment
668:
In this example with 3x+2x−7x+2, the polynomial's line segments are first drawn on a sheet of paper (black). Lines passing through reflections of the start and end points in the second and third segments, respectively (faint circle and square), and parallel to them (grey lines) are drawn.
224:
is a root of this polynomial. For every real zero of the polynomial there will be one unique initial angle and path that will land on the terminus. A quadratic with two real roots, for example, will have exactly two angles that satisfy the above conditions.
575:
The construction can also be done using clockwise turns instead of counterclockwise turns. When a path is interpreted using the other convention, it corresponds to the mirrored polynomial (every odd coefficient sign changed) and the roots are negated.
540:
are successively generated as distances between the vertices of the polynomial and root paths. For a root of the polynomial the final value is zero, so the last vertex coincides with the polynomial path terminus.
579:
When the right-angle path is traversed in the other direction but the same direction convention, it corresponds to the reversed mirrored polynomial and the roots are the negative reciprocals of the original roots.
355:
538:
232:
triangles, but with the vertices of the root path displaced from the polynomial path by a distance equal to the imaginary part of the root. In this case the root path will not be rectangular.
978:
127:−1 showing how negative coefficients and extended segments are handled. Each number shown on a colored line is the negative of its slope and hence a real root of the polynomial.
443:
619:−2, the polynomial's line segments are first drawn in black, as above. A circle is drawn with the straight line segment joining the start and end points forming a diameter.
214:
178:
385:
626:. Intersects of this circle with the middle segment of Lill's method, extended if needed, thus define the two angled paths in Lill's method, coloured blue and red.
549:
A solution line giving a root is similar to the Lill's construction for the polynomial with that root removed, because the visual construction is analogous to the
971:
39:+2 using Lill's method. Black segments are labeled with their lengths (coefficients in the equation), while each colored line with initial slope
964:
780:
749:
724:
1213:
1234:
742:"Résolution graphique des équations numériques de tous degrés à une seule inconnue, et description d'un instrument inventé dans ce but"
1134:
247:
803:
1275:
1345:
1041:
448:
1072:
89:
of other right-angle paths, also connecting the start to the terminus, but with vertices on the lines of the first path.
1220:
987:
1376:
1270:
650:
85:, with lengths equal to the coefficients of the polynomial. The roots of the polynomial can then be found as the
1011:
1381:
1305:
1241:
139:, reflected off of each line segment at a right angle (not necessarily the "natural" angle of reflection), and
1147:
622:
According to Thales's theorem, the triangle containing these points and any other point on the circle is a
1391:
1031:
880:
569:
67:
565:
229:
1016:
390:
1396:
1191:
1021:
1001:
1158:
1139:
605:
716:
1320:
1143:
1118:
903:
861:
550:
59:
588:
241:
1386:
1340:
1227:
1098:
853:
720:
641:
558:
183:
147:
19:
1300:
1265:
1168:
1153:
1036:
895:
845:
804:"Visualizing solutions to n-th degree algebraic equations using right-angle geometric paths"
772:
741:
708:
554:
360:
1280:
1108:
1093:
830:
75:
1067:
899:
709:
689:, which is based on a slightly modified version of Lill's method for a normed quadratic.
1350:
1325:
1315:
1310:
1295:
1290:
1173:
1006:
686:
623:
1370:
1103:
865:
807:
654:
922:
1355:
1285:
1057:
907:
1335:
1026:
773:"Résolution graphique des équations algébriques qui ont des racines imaginaires"
82:
71:
56:
48:
956:
1330:
1163:
1088:
951:
849:
564:
From the symmetry of the diagram, it can easily be seen that the roots of the
140:
63:
857:
1248:
1062:
653:
showed how Lill's method could be adapted to solve cubic equations using
97:
220:
so that the path lands on the terminus, the negative of the tangent of
81:
Lill's method involves drawing a path of straight line segments making
1113:
952:
Mathologer video: "Solving equations by shooting turtles with lasers"
587:
96:
86:
18:
946:
240:
The construction in effect evaluates the polynomial according to
350:{\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\cdots }
960:
23:
Finding roots −2, −1 (repeated root), and −1/3 of the quartic 3
711:
Uncommon
Mathematical Excursions: Polynomia and Related Realms
881:"Solving Cubics With Creases: The Work of Beloch and Lill"
74:
in 1867. A later paper by Lill dealt with the problem of
661:
th degree equation with a real root can be solved using
629:
The negative of the gradients of their first segments,
228:
For complex roots, one also needs to find a series of
135:
A line is then launched from the origin at some angle
533:{\displaystyle ((a_{n}x+a_{n-1})x+a_{n-2})x,\ \dots }
451:
393:
363:
250:
186:
150:
1258:
1205:
1184:
1127:
1081:
1050:
994:
16:
Graphical method for the real roots of a polynomial
608:to find the real roots of a quadratic polynomial.
532:
437:
379:
349:
208:
172:
43:and the same endpoint corresponds to a real root.
584:Finding quadratic roots using Thales's theorem
972:
657:. If simultaneous folds are allowed then any
8:
677:, yield the real roots 1/3, 1 and −2.
923:"One-, Two-, and Multi-Fold Origami Axioms"
979:
965:
957:
921:Roger C. Alperin; Robert J. Lang (2009).
503:
478:
462:
450:
417:
401:
392:
368:
362:
329:
313:
294:
278:
265:
255:
249:
191:
185:
155:
149:
640:
633:, yield the real roots 1/3 and −2.
70:. It was developed by Austrian engineer
699:
553:of the polynomial by a linear (root)
7:
1214:Geometric Exercises in Paper Folding
900:10.4169/amer.math.monthly.118.04.307
806:. www.concentric.net. Archived from
797:
795:
766:
764:
144:corresponding to the coefficient of
1235:A History of Folding in Mathematics
781:Nouvelles Annales de Mathématiques
750:Nouvelles Annales de Mathématiques
55:is a visual method of finding the
14:
829:Tabachnikov, Serge (2017-03-01).
637:Finding roots using paper folding
438:{\displaystyle (a_{n}x+a_{n-1})x}
1135:Alexandrov's uniqueness theorem
604:Lill's method can be used with
838:The Mathematical Intelligencer
515:
490:
455:
452:
429:
394:
1:
1073:Regular paperfolding sequence
888:American Mathematical Monthly
879:Thomas C. Hull (April 2011).
1221:Geometric Folding Algorithms
988:Mathematics of paper folding
947:Animation for Lill's Method
802:Bradford, Phillips Verner.
1413:
1271:Margherita Piazzola Beloch
651:Margherita Piazzola Beloch
1042:Yoshizawa–Randlett system
850:10.1007/s00283-016-9681-y
831:"Polynomials as Polygons"
93:Description of the method
1242:Origami Polyhedra Design
645:Find roots of 3x+2x−7x+2
572:of the original roots.
209:{\displaystyle x^{n-2},}
173:{\displaystyle x^{n-1},}
665:–2 simultaneous folds.
583:
101:Finding roots −1/2, −1/
1032:Napkin folding problem
646:
611:In this example with 3
601:
534:
439:
381:
380:{\displaystyle a_{n}x}
351:
210:
174:
128:
44:
644:
591:
545:Additional properties
535:
440:
382:
352:
244:. For the polynomial
211:
175:
100:
22:
1192:Fold-and-cut theorem
1148:Steffen's polyhedron
1012:Huzita–Hatori axioms
1002:Big-little-big lemma
449:
391:
361:
248:
184:
148:
1140:Flexible polyhedron
771:M. E. Lill (1868).
740:M. E. Lill (1867).
707:Dan Kalman (2009).
566:reversed polynomial
1377:1867 introductions
1321:Toshikazu Kawasaki
1144:Bricard octahedron
1119:Yoshimura buckling
1017:Kawasaki's theorem
647:
602:
592:Finding roots of 3
551:synthetic division
530:
435:
377:
347:
206:
170:
129:
45:
1364:
1363:
1228:Geometric Origami
1099:Paper bag problem
1022:Maekawa's theorem
726:978-0-88385-341-2
526:
1404:
1301:David A. Huffman
1266:Roger C. Alperin
1169:Source unfolding
1037:Pureland origami
981:
974:
967:
958:
934:
933:
927:
918:
912:
911:
885:
876:
870:
869:
835:
826:
820:
819:
817:
815:
799:
790:
789:
777:
768:
759:
758:
746:
737:
731:
730:
715:. AMS. pp.
714:
704:
606:Thales's theorem
539:
537:
536:
531:
524:
514:
513:
489:
488:
467:
466:
444:
442:
441:
436:
428:
427:
406:
405:
386:
384:
383:
378:
373:
372:
356:
354:
353:
348:
340:
339:
324:
323:
305:
304:
289:
288:
270:
269:
260:
259:
223:
219:
215:
213:
212:
207:
202:
201:
179:
177:
176:
171:
166:
165:
138:
114:
113:
107:
106:
62:of a univariate
1412:
1411:
1407:
1406:
1405:
1403:
1402:
1401:
1382:1867 in science
1367:
1366:
1365:
1360:
1346:Joseph O'Rourke
1281:Robert Connelly
1254:
1201:
1180:
1123:
1109:Schwarz lantern
1094:Modular origami
1077:
1046:
990:
985:
943:
938:
937:
925:
920:
919:
915:
883:
878:
877:
873:
833:
828:
827:
823:
813:
811:
801:
800:
793:
775:
770:
769:
762:
744:
739:
738:
734:
727:
706:
705:
701:
696:
683:
639:
586:
547:
499:
474:
458:
447:
446:
413:
397:
389:
388:
364:
359:
358:
325:
309:
290:
274:
261:
251:
246:
245:
242:Horner's method
238:
221:
217:
187:
182:
181:
151:
146:
145:
136:
111:
109:
104:
102:
95:
17:
12:
11:
5:
1410:
1408:
1400:
1399:
1394:
1389:
1384:
1379:
1369:
1368:
1362:
1361:
1359:
1358:
1353:
1351:Tomohiro Tachi
1348:
1343:
1338:
1333:
1328:
1326:Robert J. Lang
1323:
1318:
1316:Humiaki Huzita
1313:
1308:
1303:
1298:
1296:Rona Gurkewitz
1293:
1291:Martin Demaine
1288:
1283:
1278:
1273:
1268:
1262:
1260:
1256:
1255:
1253:
1252:
1245:
1238:
1231:
1224:
1217:
1209:
1207:
1203:
1202:
1200:
1199:
1194:
1188:
1186:
1182:
1181:
1179:
1178:
1177:
1176:
1174:Star unfolding
1171:
1166:
1161:
1151:
1137:
1131:
1129:
1125:
1124:
1122:
1121:
1116:
1111:
1106:
1101:
1096:
1091:
1085:
1083:
1079:
1078:
1076:
1075:
1070:
1065:
1060:
1054:
1052:
1048:
1047:
1045:
1044:
1039:
1034:
1029:
1024:
1019:
1014:
1009:
1007:Crease pattern
1004:
998:
996:
992:
991:
986:
984:
983:
976:
969:
961:
955:
954:
949:
942:
941:External links
939:
936:
935:
913:
894:(4): 307–315.
871:
821:
791:
760:
732:
725:
698:
697:
695:
692:
691:
690:
687:Carlyle circle
682:
679:
638:
635:
624:right triangle
585:
582:
559:Ruffini's rule
546:
543:
529:
523:
520:
517:
512:
509:
506:
502:
498:
495:
492:
487:
484:
481:
477:
473:
470:
465:
461:
457:
454:
434:
431:
426:
423:
420:
416:
412:
409:
404:
400:
396:
376:
371:
367:
357:the values of
346:
343:
338:
335:
332:
328:
322:
319:
316:
312:
308:
303:
300:
297:
293:
287:
284:
281:
277:
273:
268:
264:
258:
254:
237:
234:
216:etc. Choosing
205:
200:
197:
194:
190:
169:
164:
161:
158:
154:
115:of the cubic 4
94:
91:
15:
13:
10:
9:
6:
4:
3:
2:
1409:
1398:
1395:
1393:
1392:Paper folding
1390:
1388:
1385:
1383:
1380:
1378:
1375:
1374:
1372:
1357:
1354:
1352:
1349:
1347:
1344:
1342:
1339:
1337:
1334:
1332:
1329:
1327:
1324:
1322:
1319:
1317:
1314:
1312:
1309:
1307:
1304:
1302:
1299:
1297:
1294:
1292:
1289:
1287:
1284:
1282:
1279:
1277:
1274:
1272:
1269:
1267:
1264:
1263:
1261:
1257:
1251:
1250:
1246:
1244:
1243:
1239:
1237:
1236:
1232:
1230:
1229:
1225:
1223:
1222:
1218:
1216:
1215:
1211:
1210:
1208:
1204:
1198:
1197:Lill's method
1195:
1193:
1190:
1189:
1187:
1185:Miscellaneous
1183:
1175:
1172:
1170:
1167:
1165:
1162:
1160:
1157:
1156:
1155:
1152:
1149:
1145:
1141:
1138:
1136:
1133:
1132:
1130:
1126:
1120:
1117:
1115:
1112:
1110:
1107:
1105:
1104:Rigid origami
1102:
1100:
1097:
1095:
1092:
1090:
1087:
1086:
1084:
1082:3d structures
1080:
1074:
1071:
1069:
1066:
1064:
1061:
1059:
1056:
1055:
1053:
1051:Strip folding
1049:
1043:
1040:
1038:
1035:
1033:
1030:
1028:
1025:
1023:
1020:
1018:
1015:
1013:
1010:
1008:
1005:
1003:
1000:
999:
997:
993:
989:
982:
977:
975:
970:
968:
963:
962:
959:
953:
950:
948:
945:
944:
940:
932:. A K Peters.
931:
924:
917:
914:
909:
905:
901:
897:
893:
889:
882:
875:
872:
867:
863:
859:
855:
851:
847:
843:
839:
832:
825:
822:
810:on 2 May 2010
809:
805:
798:
796:
792:
787:
783:
782:
774:
767:
765:
761:
756:
752:
751:
743:
736:
733:
728:
722:
718:
713:
712:
703:
700:
693:
688:
685:
684:
680:
678:
676:
670:
666:
664:
660:
656:
655:paper folding
652:
643:
636:
634:
632:
627:
625:
620:
618:
614:
609:
607:
599:
595:
590:
581:
577:
573:
571:
567:
562:
560:
556:
552:
544:
542:
527:
521:
518:
510:
507:
504:
500:
496:
493:
485:
482:
479:
475:
471:
468:
463:
459:
432:
424:
421:
418:
414:
410:
407:
402:
398:
374:
369:
365:
344:
341:
336:
333:
330:
326:
320:
317:
314:
310:
306:
301:
298:
295:
291:
285:
282:
279:
275:
271:
266:
262:
256:
252:
243:
235:
233:
231:
226:
203:
198:
195:
192:
188:
167:
162:
159:
156:
152:
142:
133:
126:
122:
118:
99:
92:
90:
88:
84:
79:
77:
73:
69:
65:
61:
58:
54:
53:Lill's method
50:
42:
38:
34:
30:
26:
21:
1356:Eve Torrence
1286:Erik Demaine
1247:
1240:
1233:
1226:
1219:
1212:
1206:Publications
1196:
1068:Möbius strip
1058:Dragon curve
995:Flat folding
929:
916:
891:
887:
874:
844:(1): 41–43.
841:
837:
824:
812:. Retrieved
808:the original
785:
779:
754:
748:
735:
710:
702:
674:
671:
667:
662:
658:
648:
630:
628:
621:
616:
612:
610:
603:
597:
593:
578:
574:
563:
548:
239:
227:
134:
130:
124:
120:
116:
83:right angles
80:
52:
46:
40:
36:
32:
28:
24:
1397:Polynomials
1341:Kōryō Miura
1336:Jun Maekawa
1311:Kôdi Husimi
1027:Map folding
570:reciprocals
236:Explanation
72:Eduard Lill
49:mathematics
1371:Categories
1331:Anna Lubiw
1164:Common net
1089:Miura fold
814:3 February
788:: 363–367.
757:: 359–362.
694:References
64:polynomial
1249:Origamics
1128:Polyhedra
866:126072703
858:1866-7414
528:…
508:−
483:−
422:−
345:⋯
334:−
318:−
299:−
283:−
196:−
160:−
141:refracted
1387:Geometry
1306:Tom Hull
1276:Yan Chen
1159:Blooming
1063:Flexagon
681:See also
649:In 1936
568:are the
180:then of
108:, and 1/
908:2540978
230:similar
110:√
103:√
78:roots.
76:complex
66:of any
1259:People
1114:Sonobe
906:
864:
856:
723:
525:
87:slopes
68:degree
930:4OSME
926:(PDF)
904:S2CID
884:(PDF)
862:S2CID
834:(PDF)
784:. 2.
776:(PDF)
753:. 2.
745:(PDF)
719:–22.
555:monic
60:roots
854:ISSN
816:2012
721:ISBN
57:real
1154:Net
896:doi
892:118
846:doi
561:).
47:In
35:+11
31:+19
27:+13
1373::
1146:,
928:.
902:.
890:.
886:.
860:.
852:.
842:39
840:.
836:.
794:^
778:.
763:^
747:.
717:13
615:+5
600:−2
596:+5
445:,
387:,
123:−2
119:+2
51:,
1150:)
1142:(
980:e
973:t
966:v
910:.
898::
868:.
848::
818:.
786:7
755:6
729:.
675:m
663:n
659:n
631:m
617:x
613:x
598:x
594:x
557:(
522:,
519:x
516:)
511:2
505:n
501:a
497:+
494:x
491:)
486:1
480:n
476:a
472:+
469:x
464:n
460:a
456:(
453:(
433:x
430:)
425:1
419:n
415:a
411:+
408:x
403:n
399:a
395:(
375:x
370:n
366:a
342:+
337:2
331:n
327:x
321:2
315:n
311:a
307:+
302:1
296:n
292:x
286:1
280:n
276:a
272:+
267:n
263:x
257:n
253:a
222:θ
218:θ
204:,
199:2
193:n
189:x
168:,
163:1
157:n
153:x
137:θ
125:x
121:x
117:x
112:2
105:2
41:m
37:x
33:x
29:x
25:x
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.