84:
234:
20:
304:
A planar power diagram may also be interpreted as a planar cross-section of an unweighted three-dimensional
Voronoi diagram. In this interpretation, the set of circle centers in the cross-section plane are the perpendicular projections of the three-dimensional Voronoi sites, and the squared radius of
295:
include the additively weighted
Voronoi diagram, in which each site has a weight that is added to its distance before comparing it to the distances to the other sites, and the multiplicatively weighted Voronoi diagram, in which the weight of a site is multiplied by its distance before comparing it to
409:
The power diagram may be used as part of an efficient algorithm for computing the volume of a union of spheres. Intersecting each sphere with its power diagram cell gives its contribution to the total union, from which the volume may be computed in time proportional to the complexity of the power
417:
for testing whether a point belongs to a union of disks, algorithms for constructing the boundary of a union of disks, and algorithms for finding the closest two balls in a set of balls. It is also used for solving the semi-discrete
453:
point light sources. Power diagrams have appeared in the literature under other names including the "Laguerre–Voronoi diagram", "Dirichlet cell complex", "radical
Voronoi tesselation" and "sectional Dirichlet tesselation".
300:
before comparing it to other squared distances. In the case that all the circle radii are equal, this subtraction makes no difference to the comparison, and the power diagram coincides with the
Voronoi diagram.
296:
the distances to the other sites. In contrast, in the power diagram, we may view each circle center as a site, and each circle's squared radius as a weight that is subtracted from the
404:
237:
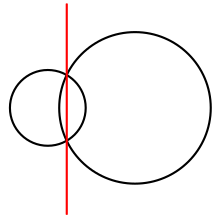
The radical axis of two intersecting circles. The power diagram of the two circles is the partition of the plane into two halfplanes formed by this line.
851:
291:
of a set of point sites, a partition of the plane into cells within which one of the sites is closer than all the other sites. Other forms of
419:
253:
or chordale of the two circles. Along the radical axis, both circles have equal power. More generally, in any power diagram, each cell
1013:
316:
Like the
Voronoi diagram, the power diagram may be generalized to Euclidean spaces of any dimension. The power diagram of
83:
927:
297:
922:
529:
Imai, Hiroshi; Iri, Masao; Murota, Kazuo (1985), "Voronoĭ diagram in the
Laguerre geometry and its applications",
75:, and coincides with the Voronoi diagram of the circle centers in the case that all the circles have equal radii.
588:
531:
292:
359:
422:
problem which in turn has numerous applications, such as early universe reconstruction or fluid dynamics.
28:
845:
233:
888:
632:
739:
71:
is smaller than the power distance to the other circles. The power diagram is a form of generalized
972:
804:"A fast semidiscrete optimal transport algorithm for a unique reconstruction of the early Universe"
653:
639:, EATCS Monographs on Theoretical Computer Science, vol. 10, Springer-Verlag, pp. 327–328
473:
279:
of the diagram, which are the radical centers of the three circles whose cells meet at the vertex.
144:
952:
904:
878:
866:
815:
784:
735:
678:
498:
163:
may be extended to all points in the plane, regardless of whether they are inside or outside of
348:). More generally, because of the equivalence with higher-dimensional halfspace intersections,
1018:
833:
776:
583:
276:
981:
936:
896:
825:
803:
768:
715:
662:
597:
540:
482:
108:
64:
993:
948:
674:
609:
552:
494:
989:
944:
670:
605:
548:
490:
434:
288:
72:
52:
309:
minus the squared distance of the corresponding site from the cross-section plane, where
892:
438:
433:
traces the definition of the power distance to the work of 19th-century mathematicians
414:
263:
867:"Partial optimal transport for a constant-volume Lagrangian mesh with free boundaries"
340:
Two-dimensional power diagrams may be constructed by an algorithm that runs in time O(
1007:
956:
908:
682:
502:
700:
788:
250:
970:
Aurenhammer, F.; Imai, H. (1988), "Geometric relations among Voronoĭ diagrams",
651:
Ash, Peter F.; Bolker, Ethan D. (1986), "Generalized
Dirichlet tessellations",
900:
756:
696:
837:
829:
780:
445:
defined power diagrams and used them to show that the boundary of a union of
471:
Linhart, J. (1981), "Dirichletsche
Zellenkomplexe mit maximaler Eckenzahl",
246:
266:, the intersection of the halfspaces bounded by the radical axes of circle
19:
324:
dimensions is combinatorially equivalent to the intersection of a set of
356: > 2) may be constructed by an algorithm that runs in time
985:
940:
772:
720:
666:
486:
56:
802:
Levy, Bruno; Mohayaee, Roya; von
Hausegger, Sebastian (2021-07-13).
601:
544:
883:
820:
586:(1987), "Power diagrams: properties, algorithms and applications",
232:
82:
59:
cells defined from a set of circles. The cell for a given circle
738:; Zhang, Li (1998), "Euclidean proximity and power diagrams",
755:
Aurenhammer, F.; Hoffmann, F.; Aronov, B. (January 1998).
313:
is chosen large enough to make all these radii positive.
139:
from the center of the circle, and the circle has radius
287:
The power diagram may be seen as a weighted form of the
449:
circular disks can always be illuminated from at most 2
757:"Minkowski-Type Theorems and Least-Squares Clustering"
362:
119:is the square of the length of a line segment from
741:10th Canadian Conference on Computational Geometry
398:
245: = 2, the power diagram consists of two
928:Acta Mathematica Academiae Scientiarum Hungaricae
808:Monthly Notices of the Royal Astronomical Society
275:with each other circle. Triples of cells meet at
699:; Bhattacharya, Binay K.; Imai, Hiroshi (1988),
701:"Computing the volume of the union of spheres"
413:Other applications of power diagrams include
8:
388:
374:
430:
332: + 1 dimensions, and vice versa.
442:
882:
819:
719:
380:
373:
361:
63:consists of all the points for which the
925:(1977), "Illumination of convex discs",
399:{\displaystyle O(n^{\lceil d/2\rceil })}
18:
524:
522:
520:
518:
516:
514:
512:
463:
843:
226:is the circle minimizing the power of
627:
625:
623:
621:
619:
578:
576:
574:
572:
570:
568:
566:
564:
562:
7:
637:Algorithms in Combinatorial Geometry
171:have zero power, and points inside
850:: CS1 maint: unflagged free DOI (
204:(called cells), such that a point
14:
352:-dimensional power diagrams (for
249:, separated by a line called the
191:is a partition of the plane into
871:Journal of Computational Physics
16:Partition of the Euclidean plane
635:(1987), "13.6 Power Diagrams",
49:sectional Dirichlet tesselation
23:A power diagram of four circles
393:
366:
178:The power diagram of a set of
1:
865:Lévy, Bruno (February 2022).
328:upward-facing halfspaces in
336:Algorithms and applications
45:radical Voronoi tesselation
1035:
305:each circle is a constant
298:squared Euclidean distance
901:10.1016/j.jcp.2021.110838
589:SIAM Journal on Computing
532:SIAM Journal on Computing
91:outside of a given circle
293:weighted Voronoi diagram
51:, is a partition of the
37:Laguerre–Voronoi diagram
1014:Computational geometry
830:10.1093/mnras/stab1676
420:optimal transportation
400:
238:
92:
41:Dirichlet cell complex
29:computational geometry
24:
633:Edelsbrunner, Herbert
401:
283:Related constructions
236:
175:have negative power.
87:The power of a point
86:
22:
360:
973:Geometriae Dedicata
893:2022JCoPh.45110838L
708:The Visual Computer
654:Geometriae Dedicata
474:Geometriae Dedicata
159: −
155:. The same formula
151: −
145:Pythagorean theorem
131:. Equivalently, if
103:is a point outside
986:10.1007/BF00181613
941:10.1007/BF01895856
773:10.1007/PL00009187
721:10.1007/BF01901190
667:10.1007/BF00164401
487:10.1007/BF00149360
431:Aurenhammer (1987)
396:
239:
93:
25:
443:Fejes Tóth (1977)
127:of tangency with
1026:
998:
996:
967:
961:
959:
935:(3–4): 355–360,
919:
913:
912:
886:
862:
856:
855:
849:
841:
823:
814:(1): 1165–1185.
799:
793:
792:
752:
746:
744:
736:Guibas, Leonidas
732:
726:
724:
723:
705:
693:
687:
685:
648:
642:
640:
629:
614:
612:
580:
557:
555:
526:
507:
505:
468:
405:
403:
402:
397:
392:
391:
384:
217:whenever circle
115:with respect to
99:is a circle and
35:, also called a
1034:
1033:
1029:
1028:
1027:
1025:
1024:
1023:
1004:
1003:
1002:
1001:
969:
968:
964:
921:
920:
916:
864:
863:
859:
842:
801:
800:
796:
754:
753:
749:
734:
733:
729:
703:
695:
694:
690:
650:
649:
645:
631:
630:
617:
602:10.1137/0216006
584:Aurenhammer, F.
582:
581:
560:
545:10.1137/0214006
528:
527:
510:
470:
469:
465:
460:
435:Edmond Laguerre
428:
415:data structures
369:
358:
357:
344: log
338:
289:Voronoi diagram
285:
274:
261:
225:
216:
203:
190:
147:) the power is
143:, then (by the
81:
73:Voronoi diagram
53:Euclidean plane
17:
12:
11:
5:
1032:
1030:
1022:
1021:
1016:
1006:
1005:
1000:
999:
962:
923:Fejes Tóth, L.
914:
857:
794:
747:
727:
714:(6): 323–328,
688:
661:(2): 209–243,
643:
615:
558:
508:
481:(3): 363–367,
462:
461:
459:
456:
439:Georgy Voronoy
427:
424:
395:
390:
387:
383:
379:
376:
372:
368:
365:
337:
334:
284:
281:
270:
264:convex polygon
257:
221:
212:
199:
186:
80:
77:
65:power distance
15:
13:
10:
9:
6:
4:
3:
2:
1031:
1020:
1017:
1015:
1012:
1011:
1009:
995:
991:
987:
983:
979:
975:
974:
966:
963:
958:
954:
950:
946:
942:
938:
934:
930:
929:
924:
918:
915:
910:
906:
902:
898:
894:
890:
885:
880:
876:
872:
868:
861:
858:
853:
847:
839:
835:
831:
827:
822:
817:
813:
809:
805:
798:
795:
790:
786:
782:
778:
774:
770:
766:
762:
758:
751:
748:
743:
742:
737:
731:
728:
722:
717:
713:
709:
702:
698:
692:
689:
684:
680:
676:
672:
668:
664:
660:
656:
655:
647:
644:
638:
634:
628:
626:
624:
622:
620:
616:
611:
607:
603:
599:
595:
591:
590:
585:
579:
577:
575:
573:
571:
569:
567:
565:
563:
559:
554:
550:
546:
542:
539:(1): 93–105,
538:
534:
533:
525:
523:
521:
519:
517:
515:
513:
509:
504:
500:
496:
492:
488:
484:
480:
476:
475:
467:
464:
457:
455:
452:
448:
444:
440:
436:
432:
425:
423:
421:
416:
411:
407:
385:
381:
377:
370:
363:
355:
351:
347:
343:
335:
333:
331:
327:
323:
319:
314:
312:
308:
302:
299:
294:
290:
282:
280:
278:
273:
269:
265:
260:
256:
252:
248:
244:
235:
231:
229:
224:
220:
215:
211:
207:
202:
198:
194:
189:
185:
181:
176:
174:
170:
166:
162:
158:
154:
150:
146:
142:
138:
135:has distance
134:
130:
126:
122:
118:
114:
110:
106:
102:
98:
90:
85:
78:
76:
74:
70:
66:
62:
58:
54:
50:
46:
42:
38:
34:
33:power diagram
30:
21:
980:(1): 65–75,
977:
971:
965:
932:
926:
917:
874:
870:
860:
846:cite journal
811:
807:
797:
767:(1): 61–76.
764:
761:Algorithmica
760:
750:
740:
730:
711:
707:
691:
658:
652:
646:
636:
596:(1): 78–96,
593:
587:
536:
530:
478:
472:
466:
450:
446:
429:
412:
408:
353:
349:
345:
341:
339:
329:
325:
321:
317:
315:
310:
306:
303:
286:
271:
267:
258:
254:
251:radical axis
242:
241:In the case
240:
227:
222:
218:
213:
209:
205:
200:
196:
192:
187:
183:
179:
177:
172:
168:
167:: points on
164:
160:
156:
152:
148:
140:
136:
132:
128:
124:
120:
116:
112:
104:
100:
96:
94:
88:
68:
60:
48:
44:
40:
36:
32:
26:
697:Avis, David
320:spheres in
208:belongs to
123:to a point
107:, then the
1008:Categories
884:2106.03936
877:: 110838.
821:2012.09074
458:References
247:halfplanes
79:Definition
957:122510545
909:235406800
838:0035-8711
781:0178-4617
683:120383767
503:120072781
410:diagram.
389:⌉
375:⌈
57:polygonal
1019:Diagrams
277:vertices
195:regions
182:circles
994:0950323
949:0464065
889:Bibcode
789:5409198
675:0833848
610:0873251
553:0774929
495:0627538
426:History
992:
955:
947:
907:
836:
787:
779:
681:
673:
608:
551:
501:
493:
953:S2CID
905:S2CID
879:arXiv
816:arXiv
785:S2CID
704:(PDF)
679:S2CID
499:S2CID
262:is a
109:power
55:into
47:or a
852:link
834:ISSN
777:ISSN
437:and
31:, a
982:doi
937:doi
897:doi
875:451
826:doi
812:506
769:doi
716:doi
663:doi
598:doi
541:doi
483:doi
111:of
95:If
67:to
27:In
1010::
990:MR
988:,
978:27
976:,
951:,
945:MR
943:,
933:29
931:,
903:.
895:.
887:.
873:.
869:.
848:}}
844:{{
832:.
824:.
810:.
806:.
783:.
775:.
765:20
763:.
759:.
710:,
706:,
677:,
671:MR
669:,
659:20
657:,
618:^
606:MR
604:,
594:16
592:,
561:^
549:MR
547:,
537:14
535:,
511:^
497:,
491:MR
489:,
479:11
477:,
441:.
406:.
230:.
43:,
39:,
997:.
984::
960:.
939::
911:.
899::
891::
881::
854:)
840:.
828::
818::
791:.
771::
745:.
725:.
718::
712:3
686:.
665::
641:.
613:.
600::
556:.
543::
506:.
485::
451:n
447:n
394:)
386:2
382:/
378:d
371:n
367:(
364:O
354:d
350:d
346:n
342:n
330:d
326:n
322:d
318:n
311:K
307:K
272:i
268:C
259:i
255:R
243:n
228:P
223:i
219:C
214:i
210:R
206:P
201:i
197:R
193:n
188:i
184:C
180:n
173:C
169:C
165:C
161:r
157:d
153:r
149:d
141:r
137:d
133:P
129:C
125:T
121:P
117:C
113:P
105:C
101:P
97:C
89:P
69:C
61:C
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.