441:
135:
1361:
102:. The case when the sets are affine spaces is special, since the iterates not only converge to a point in the intersection (assuming the intersection is non-empty) but to the orthogonal projection of the point onto the intersection. For general closed convex sets, the limit point need not be the projection. Classical work on the case of two closed convex sets shows that the
22:
1002:
1356:{\displaystyle (x_{k+1},y_{k+1})={\mathcal {P}}_{F}({\mathcal {P}}_{E}((x_{k},y_{k})))={\mathcal {P}}_{F}(({\mathcal {P}}_{C}x_{k},{\mathcal {P}}_{D}y_{k}))={\frac {1}{2}}({\mathcal {P}}_{C}(x_{k})+{\mathcal {P}}_{D}(y_{k}),({\mathcal {P}}_{C}(x_{k})+{\mathcal {P}}_{D}(y_{k})).}
1637:
580:
206:
392:
822:
716:
666:
266:
118:
of the original point. These questions are largely known for simple cases, but a topic of active research for the extensions. There are also variants of the algorithm, such as
1416:
1496:
1456:
994:
1522:
906:
877:
851:
938:
296:
1729:
J. von
Neumann. Functional Operators, volume II. Princeton University Press, Princeton, NJ, 1950. Reprint of mimeographed lecture notes first distributed in 1933.
585:
It has long been known to converge globally. Furthermore, the method is easy to generalize to more than two sets; some convergence results for this case are in.
1527:
470:
148:
304:
724:
126:
section for an overview of the variants, extensions and applications of the POCS method; a good historical background can be found in section III of.
1887:
A. Auslender. Methodes
Numeriques pour la Resolution des Problems d’Optimisation avec Constraintes. PhD thesis, Faculte des Sciences, Grenoble, 1969
110:, or that give faster convergence rates. Analysis of POCS and related methods attempt to show that the algorithm converges (and if so, find the
1803:
106:
of the iterates is linear. There are now extensions that consider cases when there are more than two sets, or when the sets are not
62:
44:
421:
119:
677:
1766:
Bauschke, H.H.; Borwein, J.M. (1993). "On the convergence of von
Neumann's alternating projection algorithm for two sets".
1739:
Gubin, L.G.; Polyak, B.T.; Raik, E.V. (1967). "The method of projections for finding the common point of convex sets".
1897:
Lewis, A. S.; Luke, D. R.; Malick, J. (2009). "Local convergence for alternating and averaged nonconvex projections".
115:
1841:
40:
602:
398:
1954:
440:
94:
sets. It is a very simple algorithm and has been rediscovered many times. The simplest case, when the sets are
1812:
1665:
1656:
Bauschke, H.H.; Borwein, J.M. (1996). "On projection algorithms for solving convex feasibility problems".
134:
32:
240:
1369:
1817:
1670:
111:
103:
1906:
1783:
1711:
1461:
1421:
947:
414:
1501:
885:
856:
830:
1916:
1856:
1822:
1775:
1748:
1703:
1675:
99:
1632:{\displaystyle x_{k+1}={\frac {1}{2}}({\mathcal {P}}_{C}(x_{k})+{\mathcal {P}}_{D}(x_{k}))}
911:
575:{\displaystyle x_{k+1}={\frac {1}{2}}({\mathcal {P}}_{C}(x_{k})+{\mathcal {P}}_{D}(x_{k}))}
274:
201:{\displaystyle {\text{find}}\;x\in \mathbb {R} ^{n}\quad {\text{such that}}\;x\in C\cap D}
672:
1948:
1787:
1752:
95:
1801:
Lewis, Adrian S.; Malick, Jérôme (2008). "Alternating
Projections on Manifolds".
387:{\displaystyle x_{k+1}={\mathcal {P}}_{C}\left({\mathcal {P}}_{D}(x_{k})\right).}
817:{\displaystyle F=\{(x,y):x\in \mathbb {R} ^{n},\,y\in \mathbb {R} ^{n},\;x=y\}.}
1920:
1679:
223:
220:
107:
91:
88:
1938:
1826:
1864:
410:
397:
The simplicity of the algorithm explains some of its popularity. If the
1779:
1715:
229:
To use the POCS algorithm, one must know how to project onto the sets
1860:
1694:
Neumann, John Von (1949). "On rings of operators. Reduction theory".
1707:
908:, use the alternating projection method. The projection of a vector
1911:
87:
method, is a method to find a point in the intersection of two
1941:
by René Escalante and Marcos Raydan (2011), published by SIAM.
424:, the solution need not be a projection onto the intersection
15:
1599:
1566:
1320:
1287:
1251:
1218:
1172:
1145:
1125:
1070:
1053:
596:
projections method using a standard trick. Consider the set
542:
509:
349:
330:
247:
1741:
U.S.S.R. Computational
Mathematics and Mathematical Physics
456:
is quite similar. For the case of two closed convex sets
711:{\displaystyle \mathbb {R} ^{n}\times \mathbb {R} ^{n}}
1720:(a reprint of lecture notes first distributed in 1933)
718:. Then define another set, also in the product space:
1530:
1504:
1464:
1424:
1372:
1005:
950:
914:
888:
859:
833:
727:
680:
605:
473:
307:
277:
243:
151:
1631:
1516:
1490:
1450:
1410:
1355:
988:
932:
900:
871:
845:
816:
710:
660:
574:
386:
290:
260:
200:
271:The algorithm starts with an arbitrary value for
142:The POCS algorithm solves the following problem:
1842:"The foundations of set theoretic estimation"
1524:, and hence we can simplify the iteration to
8:
808:
734:
655:
612:
43:. There might be a discussion about this on
661:{\displaystyle E=\{(x,y):x\in C,\;y\in D\}}
798:
645:
592:projections method can be reformulated as
182:
157:
1910:
1816:
1669:
1617:
1604:
1598:
1597:
1584:
1571:
1565:
1564:
1550:
1535:
1529:
1503:
1482:
1469:
1463:
1442:
1429:
1423:
1396:
1377:
1371:
1338:
1325:
1319:
1318:
1305:
1292:
1286:
1285:
1269:
1256:
1250:
1249:
1236:
1223:
1217:
1216:
1202:
1187:
1177:
1171:
1170:
1160:
1150:
1144:
1143:
1130:
1124:
1123:
1104:
1091:
1075:
1069:
1068:
1058:
1052:
1051:
1032:
1013:
1004:
978:
949:
913:
887:
858:
832:
789:
785:
784:
776:
767:
763:
762:
726:
702:
698:
697:
687:
683:
682:
679:
604:
560:
547:
541:
540:
527:
514:
508:
507:
493:
478:
472:
367:
354:
348:
347:
335:
329:
328:
312:
306:
282:
276:
252:
246:
245:
242:
177:
170:
166:
165:
152:
150:
63:Learn how and when to remove this message
1899:Foundations of Computational Mathematics
439:
133:
1648:
7:
417:to some point in this intersection.
123:
114:), and whether it converges to the
1804:Mathematics of Operations Research
261:{\displaystyle {\mathcal {P}}_{i}}
14:
413:generated by the algorithm will
298:and then generates the sequence
237:separately, via the projections
20:
1411:{\displaystyle x_{k+1}=y_{k+1}}
176:
1939:Alternating Projection Methods
1626:
1623:
1610:
1590:
1577:
1560:
1347:
1344:
1331:
1311:
1298:
1281:
1275:
1262:
1242:
1229:
1212:
1196:
1193:
1139:
1136:
1116:
1113:
1110:
1084:
1081:
1064:
1044:
1006:
975:
951:
927:
915:
749:
737:
627:
615:
569:
566:
553:
533:
520:
503:
422:Dykstra's projection algorithm
373:
360:
120:Dykstra's projection algorithm
1:
122:. See the references in the
1753:10.1016/0041-5553(67)90113-9
77:projections onto convex sets
1491:{\displaystyle x_{j}=y_{j}}
1451:{\displaystyle x_{0}=y_{0}}
989:{\displaystyle (x+y,x+y)/2}
1971:
83:), sometimes known as the
1921:10.1007/s10208-008-9036-y
1840:Combettes, P. L. (1993).
1680:10.1137/S0036144593251710
853:is equivalent to finding
671:which is defined in the
1849:Proceedings of the IEEE
1517:{\displaystyle j\geq 0}
901:{\displaystyle E\cap F}
872:{\displaystyle E\cap F}
846:{\displaystyle C\cap D}
409:is non-empty, then the
1827:10.1287/moor.1070.0291
1633:
1518:
1492:
1452:
1412:
1357:
990:
934:
902:
873:
847:
818:
712:
662:
576:
449:
388:
292:
262:
202:
139:
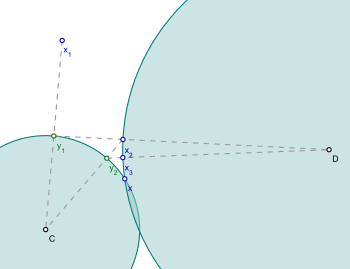
138:Example on two circles
85:alternating projection
1634:
1519:
1493:
1453:
1413:
1358:
991:
935:
933:{\displaystyle (x,y)}
903:
874:
848:
819:
713:
663:
577:
443:
389:
293:
291:{\displaystyle x_{0}}
263:
203:
137:
1528:
1502:
1462:
1422:
1370:
1003:
948:
912:
886:
857:
831:
725:
678:
603:
471:
454:averaged projections
446:averaged projections
305:
275:
241:
149:
33:confusing or unclear
1768:Set-Valued Analysis
882:To find a point in
112:rate of convergence
104:rate of convergence
41:clarify the article
1780:10.1007/bf01027691
1629:
1514:
1488:
1448:
1408:
1353:
986:
930:
898:
869:
843:
814:
708:
658:
572:
450:
436:Related algorithms
384:
288:
258:
198:
140:
98:, was analyzed by
1558:
1210:
501:
464:, it proceeds by
180:
155:
73:
72:
65:
1962:
1937:Book from 2011:
1925:
1924:
1914:
1894:
1888:
1885:
1879:
1878:
1876:
1875:
1869:
1863:. Archived from
1861:10.1109/5.214546
1846:
1837:
1831:
1830:
1820:
1798:
1792:
1791:
1763:
1757:
1756:
1736:
1730:
1727:
1721:
1719:
1690:
1684:
1683:
1673:
1653:
1638:
1636:
1635:
1630:
1622:
1621:
1609:
1608:
1603:
1602:
1589:
1588:
1576:
1575:
1570:
1569:
1559:
1551:
1546:
1545:
1523:
1521:
1520:
1515:
1497:
1495:
1494:
1489:
1487:
1486:
1474:
1473:
1457:
1455:
1454:
1449:
1447:
1446:
1434:
1433:
1417:
1415:
1414:
1409:
1407:
1406:
1388:
1387:
1362:
1360:
1359:
1354:
1343:
1342:
1330:
1329:
1324:
1323:
1310:
1309:
1297:
1296:
1291:
1290:
1274:
1273:
1261:
1260:
1255:
1254:
1241:
1240:
1228:
1227:
1222:
1221:
1211:
1203:
1192:
1191:
1182:
1181:
1176:
1175:
1165:
1164:
1155:
1154:
1149:
1148:
1135:
1134:
1129:
1128:
1109:
1108:
1096:
1095:
1080:
1079:
1074:
1073:
1063:
1062:
1057:
1056:
1043:
1042:
1024:
1023:
995:
993:
992:
987:
982:
939:
937:
936:
931:
907:
905:
904:
899:
878:
876:
875:
870:
852:
850:
849:
844:
823:
821:
820:
815:
794:
793:
788:
772:
771:
766:
717:
715:
714:
709:
707:
706:
701:
692:
691:
686:
667:
665:
664:
659:
581:
579:
578:
573:
565:
564:
552:
551:
546:
545:
532:
531:
519:
518:
513:
512:
502:
494:
489:
488:
393:
391:
390:
385:
380:
376:
372:
371:
359:
358:
353:
352:
340:
339:
334:
333:
323:
322:
297:
295:
294:
289:
287:
286:
267:
265:
264:
259:
257:
256:
251:
250:
207:
205:
204:
199:
181:
178:
175:
174:
169:
156:
153:
100:John von Neumann
75:In mathematics,
68:
61:
57:
54:
48:
24:
23:
16:
1970:
1969:
1965:
1964:
1963:
1961:
1960:
1959:
1955:Convex geometry
1945:
1944:
1934:
1932:Further reading
1929:
1928:
1896:
1895:
1891:
1886:
1882:
1873:
1871:
1867:
1844:
1839:
1838:
1834:
1818:10.1.1.416.6182
1800:
1799:
1795:
1765:
1764:
1760:
1738:
1737:
1733:
1728:
1724:
1708:10.2307/1969463
1693:
1692:J. von Neumann,
1691:
1687:
1655:
1654:
1650:
1645:
1613:
1596:
1580:
1563:
1531:
1526:
1525:
1500:
1499:
1478:
1465:
1460:
1459:
1438:
1425:
1420:
1419:
1392:
1373:
1368:
1367:
1334:
1317:
1301:
1284:
1265:
1248:
1232:
1215:
1183:
1169:
1156:
1142:
1122:
1100:
1087:
1067:
1050:
1028:
1009:
1001:
1000:
946:
945:
910:
909:
884:
883:
855:
854:
829:
828:
783:
761:
723:
722:
696:
681:
676:
675:
601:
600:
556:
539:
523:
506:
474:
469:
468:
438:
363:
346:
345:
341:
327:
308:
303:
302:
278:
273:
272:
244:
239:
238:
164:
147:
146:
132:
124:further reading
69:
58:
52:
49:
38:
25:
21:
12:
11:
5:
1968:
1966:
1958:
1957:
1947:
1946:
1943:
1942:
1933:
1930:
1927:
1926:
1905:(4): 485–513.
1889:
1880:
1855:(2): 182–208.
1832:
1793:
1774:(2): 185–212.
1758:
1731:
1722:
1702:(2): 401–485.
1685:
1671:10.1.1.49.4940
1664:(3): 367–426.
1647:
1646:
1644:
1641:
1628:
1625:
1620:
1616:
1612:
1607:
1601:
1595:
1592:
1587:
1583:
1579:
1574:
1568:
1562:
1557:
1554:
1549:
1544:
1541:
1538:
1534:
1513:
1510:
1507:
1485:
1481:
1477:
1472:
1468:
1445:
1441:
1437:
1432:
1428:
1405:
1402:
1399:
1395:
1391:
1386:
1383:
1380:
1376:
1364:
1363:
1352:
1349:
1346:
1341:
1337:
1333:
1328:
1322:
1316:
1313:
1308:
1304:
1300:
1295:
1289:
1283:
1280:
1277:
1272:
1268:
1264:
1259:
1253:
1247:
1244:
1239:
1235:
1231:
1226:
1220:
1214:
1209:
1206:
1201:
1198:
1195:
1190:
1186:
1180:
1174:
1168:
1163:
1159:
1153:
1147:
1141:
1138:
1133:
1127:
1121:
1118:
1115:
1112:
1107:
1103:
1099:
1094:
1090:
1086:
1083:
1078:
1072:
1066:
1061:
1055:
1049:
1046:
1041:
1038:
1035:
1031:
1027:
1022:
1019:
1016:
1012:
1008:
985:
981:
977:
974:
971:
968:
965:
962:
959:
956:
953:
929:
926:
923:
920:
917:
897:
894:
891:
868:
865:
862:
842:
839:
836:
825:
824:
813:
810:
807:
804:
801:
797:
792:
787:
782:
779:
775:
770:
765:
760:
757:
754:
751:
748:
745:
742:
739:
736:
733:
730:
705:
700:
695:
690:
685:
669:
668:
657:
654:
651:
648:
644:
641:
638:
635:
632:
629:
626:
623:
620:
617:
614:
611:
608:
583:
582:
571:
568:
563:
559:
555:
550:
544:
538:
535:
530:
526:
522:
517:
511:
505:
500:
497:
492:
487:
484:
481:
477:
452:The method of
437:
434:
395:
394:
383:
379:
375:
370:
366:
362:
357:
351:
344:
338:
332:
326:
321:
318:
315:
311:
285:
281:
255:
249:
209:
208:
197:
194:
191:
188:
185:
173:
168:
163:
160:
131:
128:
71:
70:
28:
26:
19:
13:
10:
9:
6:
4:
3:
2:
1967:
1956:
1953:
1952:
1950:
1940:
1936:
1935:
1931:
1922:
1918:
1913:
1908:
1904:
1900:
1893:
1890:
1884:
1881:
1870:on 2015-06-14
1866:
1862:
1858:
1854:
1850:
1843:
1836:
1833:
1828:
1824:
1819:
1814:
1810:
1806:
1805:
1797:
1794:
1789:
1785:
1781:
1777:
1773:
1769:
1762:
1759:
1754:
1750:
1746:
1742:
1735:
1732:
1726:
1723:
1717:
1713:
1709:
1705:
1701:
1697:
1689:
1686:
1681:
1677:
1672:
1667:
1663:
1659:
1652:
1649:
1642:
1640:
1618:
1614:
1605:
1593:
1585:
1581:
1572:
1555:
1552:
1547:
1542:
1539:
1536:
1532:
1511:
1508:
1505:
1483:
1479:
1475:
1470:
1466:
1443:
1439:
1435:
1430:
1426:
1418:and assuming
1403:
1400:
1397:
1393:
1389:
1384:
1381:
1378:
1374:
1350:
1339:
1335:
1326:
1314:
1306:
1302:
1293:
1278:
1270:
1266:
1257:
1245:
1237:
1233:
1224:
1207:
1204:
1199:
1188:
1184:
1178:
1166:
1161:
1157:
1151:
1131:
1119:
1105:
1101:
1097:
1092:
1088:
1076:
1059:
1047:
1039:
1036:
1033:
1029:
1025:
1020:
1017:
1014:
1010:
999:
998:
997:
983:
979:
972:
969:
966:
963:
960:
957:
954:
943:
940:onto the set
924:
921:
918:
895:
892:
889:
880:
866:
863:
860:
840:
837:
834:
827:Thus finding
811:
805:
802:
799:
795:
790:
780:
777:
773:
768:
758:
755:
752:
746:
743:
740:
731:
728:
721:
720:
719:
703:
693:
688:
674:
673:product space
652:
649:
646:
642:
639:
636:
633:
630:
624:
621:
618:
609:
606:
599:
598:
597:
595:
591:
586:
561:
557:
548:
536:
528:
524:
515:
498:
495:
490:
485:
482:
479:
475:
467:
466:
465:
463:
459:
455:
447:
442:
435:
433:
431:
427:
423:
418:
416:
412:
408:
404:
400:
381:
377:
368:
364:
355:
342:
336:
324:
319:
316:
313:
309:
301:
300:
299:
283:
279:
269:
253:
236:
232:
227:
225:
222:
218:
214:
195:
192:
189:
186:
183:
171:
161:
158:
145:
144:
143:
136:
129:
127:
125:
121:
117:
113:
109:
105:
101:
97:
96:affine spaces
93:
90:
86:
82:
78:
67:
64:
56:
46:
45:the talk page
42:
36:
34:
29:This article
27:
18:
17:
1902:
1898:
1892:
1883:
1872:. Retrieved
1865:the original
1852:
1848:
1835:
1808:
1802:
1796:
1771:
1767:
1761:
1744:
1740:
1734:
1725:
1699:
1696:Ann. of Math
1695:
1688:
1661:
1657:
1651:
1365:
944:is given by
941:
881:
826:
670:
593:
589:
587:
584:
461:
457:
453:
451:
445:
429:
425:
419:
406:
402:
399:intersection
396:
270:
234:
230:
228:
216:
212:
210:
141:
84:
80:
76:
74:
59:
50:
39:Please help
30:
1811:: 216–234.
1747:(6): 1–24.
1658:SIAM Review
594:alternating
444:Example of
224:convex sets
1874:2012-10-09
1643:References
116:projection
53:April 2018
35:to readers
1912:0709.0109
1813:CiteSeerX
1788:121602545
1666:CiteSeerX
1509:≥
893:∩
864:∩
838:∩
781:∈
759:∈
694:×
650:∈
637:∈
193:∩
187:∈
179:such that
162:∈
130:Algorithm
1949:Category
1498:for all
996:. Hence
590:averaged
415:converge
411:sequence
1716:1969463
1458:, then
448:variant
420:Unlike
31:may be
1815:
1786:
1714:
1668:
1366:Since
221:closed
211:where
108:convex
92:convex
89:closed
1907:arXiv
1868:(PDF)
1845:(PDF)
1784:S2CID
1712:JSTOR
588:The
460:and
428:and
405:and
233:and
219:are
215:and
154:find
81:POCS
1917:doi
1857:doi
1823:doi
1776:doi
1749:doi
1704:doi
1676:doi
401:of
1951::
1915:.
1901:.
1853:81
1851:.
1847:.
1821:.
1809:33
1807:.
1782:.
1770:.
1743:.
1710:.
1700:50
1698:.
1674:.
1662:38
1660:.
1639:.
879:.
432:.
268:.
226:.
1923:.
1919::
1909::
1903:9
1877:.
1859::
1829:.
1825::
1790:.
1778::
1772:1
1755:.
1751::
1745:7
1718:.
1706::
1682:.
1678::
1627:)
1624:)
1619:k
1615:x
1611:(
1606:D
1600:P
1594:+
1591:)
1586:k
1582:x
1578:(
1573:C
1567:P
1561:(
1556:2
1553:1
1548:=
1543:1
1540:+
1537:k
1533:x
1512:0
1506:j
1484:j
1480:y
1476:=
1471:j
1467:x
1444:0
1440:y
1436:=
1431:0
1427:x
1404:1
1401:+
1398:k
1394:y
1390:=
1385:1
1382:+
1379:k
1375:x
1351:.
1348:)
1345:)
1340:k
1336:y
1332:(
1327:D
1321:P
1315:+
1312:)
1307:k
1303:x
1299:(
1294:C
1288:P
1282:(
1279:,
1276:)
1271:k
1267:y
1263:(
1258:D
1252:P
1246:+
1243:)
1238:k
1234:x
1230:(
1225:C
1219:P
1213:(
1208:2
1205:1
1200:=
1197:)
1194:)
1189:k
1185:y
1179:D
1173:P
1167:,
1162:k
1158:x
1152:C
1146:P
1140:(
1137:(
1132:F
1126:P
1120:=
1117:)
1114:)
1111:)
1106:k
1102:y
1098:,
1093:k
1089:x
1085:(
1082:(
1077:E
1071:P
1065:(
1060:F
1054:P
1048:=
1045:)
1040:1
1037:+
1034:k
1030:y
1026:,
1021:1
1018:+
1015:k
1011:x
1007:(
984:2
980:/
976:)
973:y
970:+
967:x
964:,
961:y
958:+
955:x
952:(
942:F
928:)
925:y
922:,
919:x
916:(
896:F
890:E
867:F
861:E
841:D
835:C
812:.
809:}
806:y
803:=
800:x
796:,
791:n
786:R
778:y
774:,
769:n
764:R
756:x
753::
750:)
747:y
744:,
741:x
738:(
735:{
732:=
729:F
704:n
699:R
689:n
684:R
656:}
653:D
647:y
643:,
640:C
634:x
631::
628:)
625:y
622:,
619:x
616:(
613:{
610:=
607:E
570:)
567:)
562:k
558:x
554:(
549:D
543:P
537:+
534:)
529:k
525:x
521:(
516:C
510:P
504:(
499:2
496:1
491:=
486:1
483:+
480:k
476:x
462:D
458:C
430:D
426:C
407:D
403:C
382:.
378:)
374:)
369:k
365:x
361:(
356:D
350:P
343:(
337:C
331:P
325:=
320:1
317:+
314:k
310:x
284:0
280:x
254:i
248:P
235:D
231:C
217:D
213:C
196:D
190:C
184:x
172:n
167:R
159:x
79:(
66:)
60:(
55:)
51:(
47:.
37:.
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.