308:
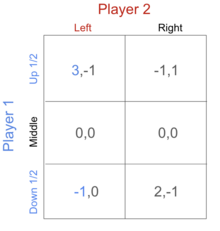
368:). When player 2 plays left, then the payoff for player 1 playing the mixed strategy of up and down is 1, when player 2 plays right, the payoff for player 1 playing the mixed strategy is 0.5. Thus regardless of whether player 2 chooses left or right, player 1 gets more from playing this mixed strategy between up and down than if the player were to play the middle strategy. In this case, we should eliminate the middle strategy for player 1 since it's been dominated by the mixed strategy of playing up and down with probability (
1014:. Consider the game on the right with payoffs of the column player omitted for simplicity. Notice that "b" is not strictly dominated by either "t" or "m" in the pure strategy sense, but it is still dominated by a strategy that would mix "t" and "m" with probability of each equal to 1/2. This is due to the fact that given any belief about the action of the column player, the mixed strategy will always yield higher expected payoff. This implies that "b" is not rationalizable.
415:
215:
262:
210:
205:
220:
277:
197:
177:
removing dominated strategies. In the first step, at most one dominated strategy is removed from the strategy space of each of the players since no rational player would ever play these strategies. This results in a new, smaller game. Some strategies—that were not dominated before—may be dominated in
185:
There are two versions of this process. One version involves only eliminating strictly dominated strategies. If, after completing this process, there is only one strategy for each player remaining, that strategy set is the unique Nash equilibrium. Moreover, iterated elimination of strictly dominated
1021:
to either "L" or "R" or any mix of the two. This is because an action that is not rationalizable can never be a best response to any opponent's strategy (pure or mixed). This would imply another version of the previous method of finding rationalizable strategies as those that survive the iterated
302:
There are instances when there is no pure strategy that dominates another pure strategy, but a mixture of two or more pure strategies can dominate another strategy. This is called
Strictly Dominant Mixed Strategies. Some authors allow for elimination of strategies dominated by a mixed strategy in
124:. Both require players to respond optimally to some belief about their opponents' actions, but Nash equilibrium requires these beliefs to be correct, while rationalizability does not. Rationalizability was first defined, independently, by Bernheim (1984) and Pearce (1984).
1025:
In games with more than two players, however, there may be strategies that are not strictly dominated, but which can never be the best response. By the iterated elimination of all such strategies one can find the rationalizable strategies for a multiplayer game.
1034:
It can be easily proved that a Nash equilibrium is a rationalizable equilibrium; however, the converse is not true. Some rationalizable equilibria are not Nash equilibria. This makes the rationalizability concept a generalization of Nash equilibrium concept.
178:
the smaller game. The first step is repeated, creating a new even smaller game, and so on. The process stops when no dominated strategy is found for any player. This process is valid since it is assumed that rationality among players is
182:, that is, each player knows that the rest of the players are rational, and each player knows that the rest of the players know that he knows that the rest of the players are rational, and so on ad infinitum (see Aumann, 1976).
1009:
Conversely, for two-player games, the set of all rationalizable strategies can be found by iterated elimination of strictly dominated strategies. For this method to hold however, one also needs to consider strict domination by
246:. However, unlike the first process, elimination of weakly dominated strategies may eliminate some Nash equilibria. As a result, the Nash equilibrium found by eliminating weakly dominated strategies may not be the
186:
strategies is path independent. That is, if at any point in the process there are multiple strictly dominated strategies, then it doesn't matter for the end result which strategies we remove first.
411:
We can demonstrate the same methods on a more complex game and solve for the rational strategies. In this scenario, the blue coloring represents the dominating numbers in the particular strategy.
147:, i.e. strategies that "never make sense" (are never a best reply to any belief about the opponents' actions). The motivation for this step is no rational player would ever choose such actions.
242:
Another version involves eliminating both strictly and weakly dominated strategies. If, at the end of the process, there is a single strategy for each player, this strategy set is also a
117:. A strategy is rationalizable if there exists some possible set of beliefs both players could have about each other's actions, that would still result in the strategy being played.
173:
The iterated elimination (or deletion, or removal) of dominated strategies (also denominated as IESDS, or IDSDS, or IRSDS) is one common technique for solving games that involves
229:
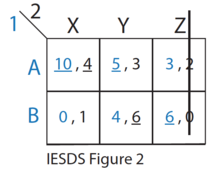
Of the remaining strategies (see IESDS Figure 2), Z is strictly dominated by Y and X for Player 2. Therefore, Player 2 will never play strategy Z. Player 1 knows this.
320:
In this scenario, for player 1, there is no pure strategy that dominates another pure strategy. Let's define the probability of player 1 playing up as p, and let p =
165:
In a game with finitely many actions, this process always terminates and leaves a non-empty set of actions for each player. These are the rationalizable actions.
235:
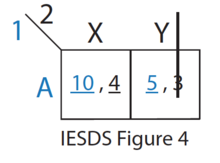
Of the remaining strategies (see IESDS Figure 4), Y is strictly dominated by X for Player 2. Therefore, Player 2 will never play Y. Player 1 knows this.
232:
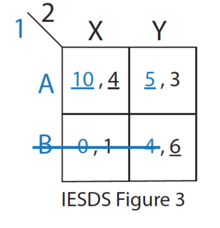
Of the remaining strategies (see IESDS Figure 3), B is strictly dominated by A for Player 1. Therefore, Player 1 will never play B. Player 2 knows this.
250:
Nash equilibrium. (In some games, if we remove weakly dominated strategies in a different order, we may end up with a different Nash equilibrium.)
1318:
539:
as tester values. The argument for mixed strategy dominance can be made if there is at least one mixed strategy that allows for dominance.
2217:
2034:
1569:
1367:
290:
In any case, if by iterated elimination of dominated strategies there is only one strategy left for each player, the game is called a
238:
Only one rationalizable strategy is left {A,X} which results in a payoff of (10,4). This is the single Nash
Equilibrium for this game.
1853:
1672:
1200:
283:
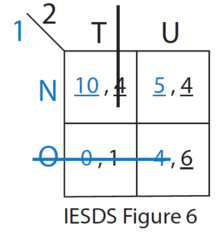
O is strictly dominated by N for Player 1. Therefore, Player 1 will never play strategy O. Player 2 knows this. (see IESDS Figure 6)
268:
O is strictly dominated by N for Player 1. Therefore, Player 1 will never play strategy O. Player 2 knows this. (see IESDS Figure 5)
226:
C is strictly dominated by A for Player 1. Therefore, Player 1 will never play strategy C. Player 2 knows this. (see IESDS Figure 1)
1474:
1943:
1484:
1813:
1994:
1412:
1387:
651:
Set up the inequality to determine whether the mixed strategy will dominate the pure strategy based on expected payoffs.
57:
2344:
1770:
1524:
1514:
1449:
307:
1564:
1544:
1171:
733:
Z will dominate pure strategy X for Player 2, and thus X can be eliminated from the rationalizable strategies for P2.
2029:
2278:
1999:
1657:
1499:
1494:
2314:
2237:
1973:
1529:
1454:
1311:
2329:
2062:
1948:
1745:
1539:
1357:
179:
2132:
1146:(beginning the cycle again). This provides an infinite set of consistent beliefs that results in row playing
2334:
1933:
1903:
1559:
1347:
2268:
2359:
2339:
2319:
1938:
1843:
1702:
1652:
1647:
1579:
1549:
1469:
1397:
1011:
1377:
1818:
1803:
934:
857:
109:. It is the most permissive possible solution concept that still requires both players to be at least
2380:
2152:
2137:
2024:
2019:
1923:
1908:
1873:
1838:
1437:
1382:
1304:
114:
2309:
1928:
1878:
1715:
1642:
1622:
1479:
1362:
1214:
1176:
286:
T is weakly dominated by U for Player 2. If Player 2 chooses U, then the final equilibrium is (N,U)
271:
U is weakly dominated by T for Player 2. If Player 2 chooses T, then the final equilibrium is (N,T)
144:
2288:
2147:
1978:
1958:
1808:
1687:
1592:
1519:
1464:
2273:
2242:
2197:
2092:
1963:
1918:
1893:
1823:
1697:
1627:
1617:
1509:
1459:
1407:
1291:
1196:
809:
759:
746:
2354:
2349:
2283:
2247:
2227:
2187:
2157:
2112:
2067:
2052:
2009:
1863:
1504:
1441:
1427:
1392:
1229:
1088:
243:
133:
121:
102:
90:
67:
38:
414:
2252:
2212:
2167:
2082:
2077:
1798:
1750:
1637:
1402:
1372:
1342:
906:
This provides an infinite chain of consistent beliefs that result in the players playing (
2117:
2192:
2182:
2172:
2107:
2097:
2087:
2072:
1868:
1848:
1833:
1828:
1788:
1755:
1740:
1735:
1725:
1534:
1195:
Joel., Watson,. Strategy : an introduction to game theory (Second ed.). New York.
2374:
2232:
2222:
2177:
2162:
2142:
1968:
1913:
1888:
1760:
1730:
1720:
1707:
1612:
1554:
1489:
1422:
1233:
1108:
1018:
829:
813:
840:
if it is reasonable for the column player to believe that the row player could play
2207:
2202:
2057:
1632:
1283:
Pearce, D. (1984) Rationalizable
Strategic Behavior and the Problem of Perfection.
1022:
elimination of strategies that are never a best response (in pure or mixed sense).
336:. We can set a mixed strategy where player 1 plays up and down with probabilities (
150:
Remove all actions which are never a best reply to any belief about the opponents'
507:
Z must be greater than the expected payoff for playing pure strategy X, assigning
113:
and know the other players are also somewhat rational, i.e. that they do not play
17:
2324:
2127:
2122:
2102:
1898:
1883:
1692:
1662:
1597:
1587:
1417:
1352:
1328:
1273:
219:
214:
106:
42:
1953:
1607:
945:
is not a best response to any strategy by the column player. For this reason,
1091:
pictured to the right. In this game the only Nash equilibrium is row playing
1858:
1778:
1602:
276:
261:
209:
204:
174:
922:) a rationalizable pair of actions. A similar process can be repeated for (
2293:
1793:
1037:
951:
756:
110:
1296:
854:
2014:
2004:
1682:
933:
As an example where not all strategies are rationalizable, consider a
413:
195:
196:
1783:
136:, the rationalizable set of actions can be computed as follows:
161:
Continue the process until no further actions can be eliminated.
1300:
820:
if he can reasonably believe that the column player could play
1290:
Ratcliff, J. (1992–1997) lecture notes on game theory, §2.2:
1134:
if it is reasonable for her to believe that column will play
1118:
if it is reasonable for her to believe that column will play
169:
Iterated elimination of strictly dominated strategies (IESDS)
836:. He can reasonably believe that the column player can play
1142:
if it is reasonable for him to believe that row will play
848:
if it is reasonable for her to believe that he could play
154:
actions—this second step is justified because each player
647:
Expected average payoff of pure strategy X: (1+1+3) = 5
1126:
if its reasonable for him to believe that row will play
1265:
Bernheim, D. (1984) Rationalizable
Strategic Behavior.
749:
strategy for
Players 1 and 2 is then (M,Z) or (3,5).
739:
For player 2, Y is dominated by the pure strategy Z.
736:
For Player 1, U is dominated by the pure strategy D.
2302:
2261:
2043:
1987:
1769:
1671:
1578:
1436:
1335:
440:For Player 2, X is dominated by the mixed strategy
86:
78:
73:
63:
53:
48:
32:
1215:"On the order of eliminating dominated strategies"
1150:. A similar argument can be given for row playing
937:pictured to the left. Row player would never play
1114:Consider the following reasoning: row can play
191:Strict Dominance Deletion Step-by-Step Example:
140:Start with the full action set for each player.
120:Rationalizability is a broader concept than a
1312:
255:Weak Dominance Deletion Step-by-Step Example:
8:
1319:
1305:
1297:
1292:"Iterated Dominance and Rationalizability"
1099:with equal probability and column playing
816:is to the right). The row player can play
306:
275:
260:
218:
213:
208:
203:
1213:Gilboa, I.; Kalai, E.; Zemel, E. (1990).
742:This leaves M dominating D for Player 1.
475:The expected payoff for playing strategy
1188:
298:Iterated elimination by mixed strategy
29:
1107:with equal probability. However, all
1030:Rationalizability and Nash equilibria
7:
844:. She can believe that he will play
158:that the other players are rational.
1368:First-player and second-player win
25:
1111:in this game are rationalizable.
1087:As an example, consider the game
1038:
855:
757:
1475:Coalition-proof Nash equilibrium
1154:, and for column playing either
27:Solution concept in game theory
1485:Evolutionarily stable strategy
1:
1413:Simultaneous action selection
58:Dominant strategy equilibrium
2345:List of games in game theory
1525:Quantal response equilibrium
1515:Perfect Bayesian equilibrium
1450:Bayes correlated equilibrium
1234:10.1016/0167-6377(90)90046-8
1814:Optional prisoner's dilemma
1545:Self-confirming equilibrium
1222:Operations Research Letters
1172:Self-confirming equilibrium
612:Expected average payoff of
577:Expected average payoff of
2397:
2279:Principal variation search
1995:Aumann's agreement theorem
1658:Strategy-stealing argument
1570:Trembling hand equilibrium
1500:Markov perfect equilibrium
1495:Mertens-stable equilibrium
2315:Combinatorial game theory
1974:Princess and monster game
1530:Quasi-perfect equilibrium
1455:Bayesian Nash equilibrium
82:D. Bernheim and D. Pearce
37:
2330:Evolutionary game theory
2063:Antoine Augustin Cournot
1949:Guess 2/3 of the average
1746:Strictly determined game
1540:Satisfaction equilibrium
1358:Escalation of commitment
1247:Gibbons, Robert (1992).
2335:Glossary of game theory
1934:Stackelberg competition
1560:Strong Nash equilibrium
1249:A Primer in Game Theory
1017:Moreover, "b" is not a
949:is not rationalizable.
2360:Tragedy of the commons
2340:List of game theorists
2320:Confrontation analysis
2030:Sprague–Grundy theorem
1550:Sequential equilibrium
1470:Correlated equilibrium
753:Constraints on beliefs
437:Step-by-step solving:
418:
200:
2133:Jean-François Mertens
1280:Cambridge: MIT Press.
574:gets the following:
417:
199:
2262:Search optimizations
2138:Jennifer Tour Chayes
2025:Revelation principle
2020:Purification theorem
1959:Nash bargaining game
1924:Bertrand competition
1909:El Farol Bar problem
1874:Electronic mail game
1839:Lewis signaling game
1383:Hierarchy of beliefs
1272:Fudenberg, Drew and
145:dominated strategies
115:dominated strategies
2310:Bounded rationality
1929:Cournot competition
1879:Rock paper scissors
1854:Battle of the sexes
1844:Volunteer's dilemma
1716:Perfect information
1643:Dominant strategies
1480:Epsilon-equilibrium
1363:Extensive-form game
1177:Strategic dominance
1042:
861:
763:
2289:Paranoid algorithm
2269:Alpha–beta pruning
2148:John Maynard Smith
1979:Rendezvous problem
1819:Traveler's dilemma
1809:Gift-exchange game
1804:Prisoner's dilemma
1721:Large Poisson game
1688:Bargaining problem
1593:Backward induction
1565:Subgame perfection
1520:Proper equilibrium
1138:. Column can play
1122:. Column can play
935:prisoner's dilemma
858:Prisoner's Dilemma
808:Consider a simple
419:
292:dominance-solvable
201:
2368:
2367:
2274:Aspiration window
2243:Suzanne Scotchmer
2198:Oskar Morgenstern
2093:Donald B. Gillies
2035:Zermelo's theorem
1964:Induction puzzles
1919:Fair cake-cutting
1894:Public goods game
1824:Coordination game
1698:Intransitive game
1628:Forward induction
1510:Pareto efficiency
1490:Gibbs equilibrium
1460:Berge equilibrium
1408:Simultaneous game
1251:. pp. 32–33.
1085:
1084:
1007:
1006:
904:
903:
810:coordination game
806:
805:
760:Coordination game
111:somewhat rational
99:Rationalizability
96:
95:
33:Rationalizability
18:Rationalizability
16:(Redirected from
2388:
2355:Topological game
2350:No-win situation
2248:Thomas Schelling
2228:Robert B. Wilson
2188:Merrill M. Flood
2158:John von Neumann
2068:Ariel Rubinstein
2053:Albert W. Tucker
1904:War of attrition
1864:Matching pennies
1505:Nash equilibrium
1428:Mechanism design
1393:Normal-form game
1348:Cooperative game
1321:
1314:
1307:
1298:
1253:
1252:
1244:
1238:
1237:
1219:
1210:
1204:
1193:
1089:matching pennies
1043:
1040:Matching pennies
1012:mixed strategies
952:
862:
764:
732:
730:
729:
726:
723:
716:
714:
713:
710:
707:
689:
687:
686:
683:
680:
670:
668:
667:
664:
661:
643:
641:
640:
637:
634:
627:
625:
624:
621:
618:
608:
606:
605:
602:
599:
592:
590:
589:
586:
583:
573:
571:
570:
567:
564:
557:
555:
554:
551:
548:
538:
536:
535:
532:
529:
522:
520:
519:
516:
513:
506:
504:
503:
500:
497:
490:
488:
487:
484:
481:
471:
469:
468:
465:
462:
455:
453:
452:
449:
446:
399:
397:
396:
393:
390:
383:
381:
380:
377:
374:
367:
365:
364:
361:
358:
351:
349:
348:
345:
342:
335:
333:
332:
329:
326:
310:
279:
264:
244:Nash equilibrium
222:
217:
212:
207:
180:common knowledge
134:normal-form game
132:Starting with a
122:Nash equilibrium
103:solution concept
91:Matching pennies
68:Nash equilibrium
39:Solution concept
30:
21:
2396:
2395:
2391:
2390:
2389:
2387:
2386:
2385:
2371:
2370:
2369:
2364:
2298:
2284:max^n algorithm
2257:
2253:William Vickrey
2213:Reinhard Selten
2168:Kenneth Binmore
2083:David K. Levine
2078:Daniel Kahneman
2045:
2039:
2015:Negamax theorem
2005:Minimax theorem
1983:
1944:Diner's dilemma
1799:All-pay auction
1765:
1751:Stochastic game
1703:Mean-field game
1674:
1667:
1638:Markov strategy
1574:
1440:
1432:
1403:Sequential game
1388:Information set
1373:Game complexity
1343:Congestion game
1331:
1325:
1262:
1257:
1256:
1246:
1245:
1241:
1217:
1212:
1211:
1207:
1194:
1190:
1185:
1168:
1130:. Row can play
1109:pure strategies
1032:
914:). This makes (
755:
727:
724:
721:
720:
718:
711:
708:
705:
704:
702:
701:Mixed strategy
695:
691:
684:
681:
678:
677:
675:
672:
665:
662:
659:
658:
656:
650:
638:
635:
632:
631:
629:
622:
619:
616:
615:
613:
603:
600:
597:
596:
594:
587:
584:
581:
580:
578:
568:
565:
562:
561:
559:
552:
549:
546:
545:
543:
533:
530:
527:
526:
524:
517:
514:
511:
510:
508:
501:
498:
495:
494:
492:
485:
482:
479:
478:
476:
466:
463:
460:
459:
457:
450:
447:
444:
443:
441:
436:
433:
430:
427:
424:
421:
403:
394:
391:
388:
387:
385:
378:
375:
372:
371:
369:
362:
359:
356:
355:
353:
346:
343:
340:
339:
337:
330:
327:
324:
323:
321:
300:
171:
130:
28:
23:
22:
15:
12:
11:
5:
2394:
2392:
2384:
2383:
2373:
2372:
2366:
2365:
2363:
2362:
2357:
2352:
2347:
2342:
2337:
2332:
2327:
2322:
2317:
2312:
2306:
2304:
2300:
2299:
2297:
2296:
2291:
2286:
2281:
2276:
2271:
2265:
2263:
2259:
2258:
2256:
2255:
2250:
2245:
2240:
2235:
2230:
2225:
2220:
2218:Robert Axelrod
2215:
2210:
2205:
2200:
2195:
2193:Olga Bondareva
2190:
2185:
2183:Melvin Dresher
2180:
2175:
2173:Leonid Hurwicz
2170:
2165:
2160:
2155:
2150:
2145:
2140:
2135:
2130:
2125:
2120:
2115:
2110:
2108:Harold W. Kuhn
2105:
2100:
2098:Drew Fudenberg
2095:
2090:
2088:David M. Kreps
2085:
2080:
2075:
2073:Claude Shannon
2070:
2065:
2060:
2055:
2049:
2047:
2041:
2040:
2038:
2037:
2032:
2027:
2022:
2017:
2012:
2010:Nash's theorem
2007:
2002:
1997:
1991:
1989:
1985:
1984:
1982:
1981:
1976:
1971:
1966:
1961:
1956:
1951:
1946:
1941:
1936:
1931:
1926:
1921:
1916:
1911:
1906:
1901:
1896:
1891:
1886:
1881:
1876:
1871:
1869:Ultimatum game
1866:
1861:
1856:
1851:
1849:Dollar auction
1846:
1841:
1836:
1834:Centipede game
1831:
1826:
1821:
1816:
1811:
1806:
1801:
1796:
1791:
1789:Infinite chess
1786:
1781:
1775:
1773:
1767:
1766:
1764:
1763:
1758:
1756:Symmetric game
1753:
1748:
1743:
1741:Signaling game
1738:
1736:Screening game
1733:
1728:
1726:Potential game
1723:
1718:
1713:
1705:
1700:
1695:
1690:
1685:
1679:
1677:
1669:
1668:
1666:
1665:
1660:
1655:
1653:Mixed strategy
1650:
1645:
1640:
1635:
1630:
1625:
1620:
1615:
1610:
1605:
1600:
1595:
1590:
1584:
1582:
1576:
1575:
1573:
1572:
1567:
1562:
1557:
1552:
1547:
1542:
1537:
1535:Risk dominance
1532:
1527:
1522:
1517:
1512:
1507:
1502:
1497:
1492:
1487:
1482:
1477:
1472:
1467:
1462:
1457:
1452:
1446:
1444:
1434:
1433:
1431:
1430:
1425:
1420:
1415:
1410:
1405:
1400:
1395:
1390:
1385:
1380:
1378:Graphical game
1375:
1370:
1365:
1360:
1355:
1350:
1345:
1339:
1337:
1333:
1332:
1326:
1324:
1323:
1316:
1309:
1301:
1295:
1294:
1288:
1287:52: 1029–1050.
1281:
1270:
1269:52: 1007–1028.
1261:
1258:
1255:
1254:
1239:
1205:
1187:
1186:
1184:
1181:
1180:
1179:
1174:
1167:
1164:
1083:
1082:
1079:
1076:
1070:
1069:
1066:
1063:
1057:
1056:
1051:
1046:
1031:
1028:
1005:
1004:
1001:
998:
992:
991:
988:
985:
979:
978:
975:
972:
966:
965:
960:
955:
902:
901:
898:
895:
889:
888:
885:
882:
876:
875:
870:
865:
804:
803:
800:
797:
791:
790:
787:
784:
778:
777:
772:
767:
754:
751:
747:rationalizable
698:4 + 5 > 5
693:
674:
655:
299:
296:
288:
287:
284:
273:
272:
269:
240:
239:
236:
233:
230:
227:
170:
167:
163:
162:
159:
148:
141:
129:
126:
94:
93:
88:
84:
83:
80:
76:
75:
71:
70:
65:
61:
60:
55:
51:
50:
46:
45:
35:
34:
26:
24:
14:
13:
10:
9:
6:
4:
3:
2:
2393:
2382:
2379:
2378:
2376:
2361:
2358:
2356:
2353:
2351:
2348:
2346:
2343:
2341:
2338:
2336:
2333:
2331:
2328:
2326:
2323:
2321:
2318:
2316:
2313:
2311:
2308:
2307:
2305:
2303:Miscellaneous
2301:
2295:
2292:
2290:
2287:
2285:
2282:
2280:
2277:
2275:
2272:
2270:
2267:
2266:
2264:
2260:
2254:
2251:
2249:
2246:
2244:
2241:
2239:
2238:Samuel Bowles
2236:
2234:
2233:Roger Myerson
2231:
2229:
2226:
2224:
2223:Robert Aumann
2221:
2219:
2216:
2214:
2211:
2209:
2206:
2204:
2201:
2199:
2196:
2194:
2191:
2189:
2186:
2184:
2181:
2179:
2178:Lloyd Shapley
2176:
2174:
2171:
2169:
2166:
2164:
2163:Kenneth Arrow
2161:
2159:
2156:
2154:
2151:
2149:
2146:
2144:
2143:John Harsanyi
2141:
2139:
2136:
2134:
2131:
2129:
2126:
2124:
2121:
2119:
2116:
2114:
2113:Herbert Simon
2111:
2109:
2106:
2104:
2101:
2099:
2096:
2094:
2091:
2089:
2086:
2084:
2081:
2079:
2076:
2074:
2071:
2069:
2066:
2064:
2061:
2059:
2056:
2054:
2051:
2050:
2048:
2042:
2036:
2033:
2031:
2028:
2026:
2023:
2021:
2018:
2016:
2013:
2011:
2008:
2006:
2003:
2001:
1998:
1996:
1993:
1992:
1990:
1986:
1980:
1977:
1975:
1972:
1970:
1967:
1965:
1962:
1960:
1957:
1955:
1952:
1950:
1947:
1945:
1942:
1940:
1937:
1935:
1932:
1930:
1927:
1925:
1922:
1920:
1917:
1915:
1914:Fair division
1912:
1910:
1907:
1905:
1902:
1900:
1897:
1895:
1892:
1890:
1889:Dictator game
1887:
1885:
1882:
1880:
1877:
1875:
1872:
1870:
1867:
1865:
1862:
1860:
1857:
1855:
1852:
1850:
1847:
1845:
1842:
1840:
1837:
1835:
1832:
1830:
1827:
1825:
1822:
1820:
1817:
1815:
1812:
1810:
1807:
1805:
1802:
1800:
1797:
1795:
1792:
1790:
1787:
1785:
1782:
1780:
1777:
1776:
1774:
1772:
1768:
1762:
1761:Zero-sum game
1759:
1757:
1754:
1752:
1749:
1747:
1744:
1742:
1739:
1737:
1734:
1732:
1731:Repeated game
1729:
1727:
1724:
1722:
1719:
1717:
1714:
1712:
1710:
1706:
1704:
1701:
1699:
1696:
1694:
1691:
1689:
1686:
1684:
1681:
1680:
1678:
1676:
1670:
1664:
1661:
1659:
1656:
1654:
1651:
1649:
1648:Pure strategy
1646:
1644:
1641:
1639:
1636:
1634:
1631:
1629:
1626:
1624:
1621:
1619:
1616:
1614:
1613:De-escalation
1611:
1609:
1606:
1604:
1601:
1599:
1596:
1594:
1591:
1589:
1586:
1585:
1583:
1581:
1577:
1571:
1568:
1566:
1563:
1561:
1558:
1556:
1555:Shapley value
1553:
1551:
1548:
1546:
1543:
1541:
1538:
1536:
1533:
1531:
1528:
1526:
1523:
1521:
1518:
1516:
1513:
1511:
1508:
1506:
1503:
1501:
1498:
1496:
1493:
1491:
1488:
1486:
1483:
1481:
1478:
1476:
1473:
1471:
1468:
1466:
1463:
1461:
1458:
1456:
1453:
1451:
1448:
1447:
1445:
1443:
1439:
1435:
1429:
1426:
1424:
1423:Succinct game
1421:
1419:
1416:
1414:
1411:
1409:
1406:
1404:
1401:
1399:
1396:
1394:
1391:
1389:
1386:
1384:
1381:
1379:
1376:
1374:
1371:
1369:
1366:
1364:
1361:
1359:
1356:
1354:
1351:
1349:
1346:
1344:
1341:
1340:
1338:
1334:
1330:
1322:
1317:
1315:
1310:
1308:
1303:
1302:
1299:
1293:
1289:
1286:
1282:
1279:
1275:
1271:
1268:
1264:
1263:
1259:
1250:
1243:
1240:
1235:
1231:
1227:
1223:
1216:
1209:
1206:
1202:
1201:9780393929348
1198:
1192:
1189:
1182:
1178:
1175:
1173:
1170:
1169:
1165:
1163:
1161:
1157:
1153:
1149:
1145:
1141:
1137:
1133:
1129:
1125:
1121:
1117:
1112:
1110:
1106:
1102:
1098:
1094:
1090:
1080:
1077:
1075:
1072:
1071:
1067:
1064:
1062:
1059:
1058:
1055:
1052:
1050:
1047:
1045:
1044:
1041:
1036:
1029:
1027:
1023:
1020:
1019:best response
1015:
1013:
1002:
999:
997:
994:
993:
989:
986:
984:
981:
980:
976:
973:
971:
968:
967:
964:
961:
959:
956:
954:
953:
950:
948:
944:
940:
936:
931:
929:
925:
921:
917:
913:
909:
899:
896:
894:
891:
890:
886:
883:
881:
878:
877:
874:
871:
869:
866:
864:
863:
860:
859:
853:
851:
847:
843:
839:
835:
831:
830:best response
827:
823:
819:
815:
814:payoff matrix
811:
801:
798:
796:
793:
792:
788:
785:
783:
780:
779:
776:
773:
771:
768:
766:
765:
762:
761:
752:
750:
748:
743:
740:
737:
734:
699:
696:
652:
648:
645:
644:(0+5+5) = 5
610:
609:(4+0+4) = 4
575:
542:Testing with
540:
473:
438:
434:
431:
428:
425:
422:
416:
412:
409:
408:
407:
401:
318:
317:
316:
311:
309:
304:
297:
295:
293:
285:
282:
281:
280:
278:
270:
267:
266:
265:
263:
258:
257:
256:
251:
249:
245:
237:
234:
231:
228:
225:
224:
223:
221:
216:
211:
206:
198:
194:
193:
192:
187:
183:
181:
176:
168:
166:
160:
157:
153:
149:
146:
142:
139:
138:
137:
135:
127:
125:
123:
118:
116:
112:
108:
104:
100:
92:
89:
85:
81:
77:
72:
69:
66:
62:
59:
56:
52:
47:
44:
40:
36:
31:
19:
2208:Peyton Young
2203:Paul Milgrom
2118:Hervé Moulin
2058:Amos Tversky
2000:Folk theorem
1711:-player game
1708:
1633:Grim trigger
1285:Econometrica
1284:
1278:Game Theory.
1277:
1267:Econometrica
1266:
1248:
1242:
1228:(2): 85–89.
1225:
1221:
1208:
1191:
1159:
1155:
1151:
1147:
1143:
1139:
1135:
1131:
1127:
1123:
1119:
1115:
1113:
1104:
1100:
1096:
1092:
1086:
1073:
1060:
1053:
1048:
1039:
1033:
1024:
1016:
1008:
995:
982:
969:
962:
957:
946:
942:
938:
932:
927:
923:
919:
915:
911:
907:
905:
892:
879:
872:
867:
856:
849:
845:
841:
837:
833:
825:
821:
817:
807:
794:
781:
774:
769:
758:
744:
741:
738:
735:
700:
697:
653:
649:
646:
628:Strategy Z:
611:
593:Strategy Y:
576:
541:
474:
439:
435:
432:
429:
426:
423:
420:
410:
405:
404:
402:
319:
314:
313:
312:
305:
301:
291:
289:
274:
259:
254:
253:
252:
247:
241:
202:
190:
189:
188:
184:
172:
164:
155:
151:
131:
119:
98:
97:
74:Significance
49:Relationship
2381:Game theory
2325:Coopetition
2128:Jean Tirole
2123:John Conway
2103:Eric Maskin
1899:Blotto game
1884:Pirate game
1693:Global game
1663:Tit for tat
1598:Bid shading
1588:Appeasement
1438:Equilibrium
1418:Solved game
1353:Determinacy
1336:Definitions
1329:game theory
1274:Jean Tirole
175:iteratively
143:Remove all
107:game theory
79:Proposed by
64:Superset of
43:game theory
1969:Trust game
1954:Kuhn poker
1623:Escalation
1618:Deterrence
1608:Cheap talk
1580:Strategies
1398:Preference
1327:Topics of
1260:References
406:Example 2:
315:Example 1:
303:this way.
128:Definition
2153:John Nash
1859:Stag hunt
1603:Collusion
1183:Footnotes
745:The only
152:remaining
54:Subset of
2375:Category
2294:Lazy SMP
1988:Theorems
1939:Deadlock
1794:Checkers
1675:of games
1442:concepts
1166:See also
941:, since
824:, since
2046:figures
1829:Chicken
1683:Auction
1673:Classes
1276:(1993)
852:, etc.
731:
719:
715:
703:
688:
676:
669:
657:
642:
630:
626:
614:
607:
595:
591:
579:
572:
560:
556:
544:
537:
525:
521:
509:
505:
493:
489:
477:
470:
458:
454:
442:
398:
386:
382:
370:
366:
354:
350:
338:
334:
322:
87:Example
1199:
1081:1, -1
1078:-1, 1
1068:-1, 1
1065:1, -1
717:Y and
456:Y and
294:game.
1784:Chess
1771:Games
1218:(PDF)
1003:1, -
1000:1, -
990:3, -
987:0, -
977:0, -
974:3, -
900:1, 1
897:3, 0
887:0, 3
884:2, 2
828:is a
812:(the
802:1, 1
799:0, 0
789:0, 0
786:1, 1
156:knows
101:is a
1465:Core
1197:ISBN
1103:and
1095:and
558:and
523:and
491:Y +
472:Z.
248:only
2044:Key
1230:doi
1158:or
930:).
832:to
692:⩼ u
673:+ u
400:).
105:in
41:in
2377::
1779:Go
1224:.
1220:.
1162:.
926:,
918:,
910:,
1709:n
1320:e
1313:t
1306:v
1236:.
1232::
1226:9
1203:.
1160:T
1156:H
1152:t
1148:h
1144:h
1140:T
1136:T
1132:t
1128:t
1124:H
1120:H
1116:h
1105:T
1101:H
1097:t
1093:h
1074:t
1061:h
1054:T
1049:H
996:b
983:m
970:t
963:R
958:L
947:c
943:c
939:c
928:B
924:b
920:A
916:a
912:A
908:a
893:d
880:c
873:D
868:C
850:a
846:a
842:a
838:A
834:A
826:a
822:A
818:a
795:b
782:a
775:B
770:A
728:2
725:/
722:1
712:2
709:/
706:1
694:X
690:Z
685:2
682:/
679:1
671:Y
666:2
663:/
660:1
654:u
639:2
636:/
633:1
623:2
620:/
617:1
604:2
601:/
598:1
588:2
585:/
582:1
569:2
566:/
563:1
553:2
550:/
547:1
534:2
531:/
528:1
518:2
515:/
512:1
502:2
499:/
496:1
486:2
483:/
480:1
467:2
464:/
461:1
451:2
448:/
445:1
395:2
392:/
389:1
384:,
379:2
376:/
373:1
363:2
360:/
357:1
352:,
347:2
344:/
341:1
331:2
328:/
325:1
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.