42:
31:
220:, if the points are on adjacent faces one candidate for the shortest path is the path crossing the common edge; the shortest path of this kind is found using a net where the two faces are also adjacent. Other candidates for the shortest path are through the surface of a third face adjacent to both (of which there are two), and corresponding nets can be used to find the shortest path in each category.
117:
186:
239:
142:. However, the polyhedron formed in this way may have different faces than the ones specified as part of the net: some of the net polygons may have folds across them, and some of the edges between net polygons may remain unfolded. Additionally, the same net may have multiple valid gluing patterns, leading to different folded polyhedra.
129:
of the polyhedron, but cutting some spanning trees may cause the polyhedron to self-overlap when unfolded, rather than forming a net. Conversely, a given net may fold into more than one different convex polyhedron, depending on the angles at which its edges are folded and the choice of which edges to
215:
over the surface between two points on the surface of a polyhedron corresponds to a straight line on a suitable net for the subset of faces touched by the path. The net has to be such that the straight line is fully within it, and one may have to consider several nets to see which gives the shortest
165:
asked whether every convex polyhedron has at least one net, or simple edge-unfolding. This question, which is also known as Dürer's conjecture, or Dürer's unfolding problem, remains unanswered. There exist non-convex polyhedra that do not have nets, and it is possible to subdivide the faces of every
265:
that are connected by their faces and all occupy the same three-dimensional space, just as the polygon faces of a net of a polyhedron are connected by their edges and all occupy the same plane. The net of the tesseract, the four-dimensional
346:
of the tree describing the pairs of faces that are opposite each other on the folded hypercube. Using this representation, the number of different unfoldings for hypercubes of dimensions 2, 3, 4, ... have been counted as
124:
Many different nets can exist for a given polyhedron, depending on the choices of which edges are joined and which are separated. The edges that are cut from a convex polyhedron to form a net must form a
1161:
120:
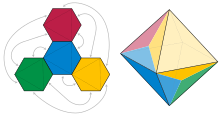
Four hexagons that, when glued to form a regular octahedron as depicted, produce folds across three of the diagonals of each hexagon. The edges between the hexagons remain unfolded.
281:
452:
336:
309:
1154:
358:
155:
130:
glue together. If a net is given together with a pattern for gluing its edges together, such that each vertex of the resulting shape has positive
1147:
1050:
546:
1396:
919:
865:
1417:
528:
1317:
139:
966:
276:
203:, a continuous non-self-intersecting motion from its flat to its folded state that keeps each face flat throughout the motion.
1458:
223:
1528:
1224:
628:
568:
1255:
597:
1403:
1170:
572:
338:
nodes describing the pattern by which pairs of faces of the hypercube are glued together to form a net, together with a
1106:
981:
493:; Sternath, Maria Luise (July 2008), "New light on the rediscovery of the Archimedean solids during the Renaissance",
917:
Miller, Ezra; Pak, Igor (2008), "Metric combinatorics of convex polyhedra: Cut loci and nonoverlapping unfoldings",
1559:
1453:
81:
in general, as they allow for physical models of polyhedra to be constructed from material such as thin cardboard.
1030:
1194:
1488:
1424:
633:
227:
1330:
1130:
685:
182:, i.e., a network of geodesics which connect vertices of the polyhedron and form a graph with convex faces.
162:
1574:
1214:
811:
428:
175:
1199:
178:. Furthermore, in 2019 Barvinok and Ghomi showed that a generalization of Dürer's conjecture fails for
1569:
1374:
1204:
1184:
995:
830:
697:
193:
105:
35:
171:
1341:
1322:
1111:
200:
189:
1564:
1503:
1326:
1301:
1125:
1013:
900:
874:
846:
820:
721:
668:
642:
510:
475:
371:
285:
863:
Barvinok, Nicholas; Ghomi, Mohammad (2019-04-03), "Pseudo-Edge
Unfoldings of Convex Polyhedra",
1523:
1410:
1281:
1089:
1070:
1046:
962:
956:
892:
739:
542:
466:
446:
424:
101:
85:
1483:
1448:
1379:
1351:
1219:
1038:
1033:(November 2014), "Science Fiction, Art, and the Fourth Dimension", in Emmer, Michele (ed.),
1003:
986:
928:
884:
838:
790:
705:
652:
534:
502:
406:
343:
339:
271:
70:
942:
717:
664:
138:, then there necessarily exists exactly one polyhedron that can be folded from it; this is
1463:
1291:
1276:
938:
713:
660:
262:
74:
62:
17:
1250:
764:
743:
999:
834:
701:
484:
318:
1533:
1508:
1498:
1493:
1478:
1473:
1356:
1189:
620:
490:
294:
131:
97:
78:
589:
1553:
1286:
725:
480:
126:
904:
850:
1538:
1468:
1240:
1017:
616:
564:
470:
185:
479:, including a net for the regular dodecahedron. However, these cannot be found in
77:
of the polyhedron. Polyhedral nets are a useful aid to the study of polyhedra and
1518:
1209:
1134:
1042:
781:
Ghomi, Mohammad (2018-01-01), "Dürer's
Unfolding Problem for Convex Polyhedra",
672:
381:
230:
puzzle which involves finding the shortest path between two points on a cuboid.
41:
30:
1139:
1093:
888:
116:
1513:
1346:
1271:
933:
709:
631:(2002), "Enumerating foldings and unfoldings between polygons and polytopes",
624:
538:
506:
386:
376:
254:
58:
896:
533:, Science Networks. Historical Studies, vol. 59, Birkhäuser, p. 8,
1431:
1098:
1079:
842:
748:
312:
267:
247:
199:
A related open question asks whether every net of a convex polyhedron has a
167:
656:
1245:
1074:
280:(1954). The same tesseract net is central to the plot of the short story
258:
243:
212:
50:
514:
238:
144:
66:
647:
1296:
795:
879:
1008:
958:
How to Fold It: The
Mathematics of Linkages, Origami and Polyhedra
825:
237:
184:
115:
40:
29:
809:
Ghomi, Mohammad (2014), "Affine unfoldings of convex polyhedra",
465:
Schreiber, Fischer, and
Sternath claim that, earlier than Dürer,
1121:
1116:
217:
1143:
690:
Mathematical
Proceedings of the Cambridge Philosophical Society
1112:
Editable
Printable Polyhedral Nets with an Interactive 3D View
530:
A History of
Folding in Mathematics: Mathematizing the Margins
351:
1, 11, 261, 9694, 502110, 33064966, 2642657228, ... (sequence
433:, Nürnberg: München, Süddeutsche Monatsheft, pp. 139–152
84:
An early instance of polyhedral nets appears in the works of
481:
online copies of the 1509 first printed edition of this work
590:"Nets: A Tool for Representing Polyhedra in Two Dimensions"
353:
574:
Geometric
Folding Algorithms: Linkages, Origami, Polyhedra
174:
showed that every convex polyhedron admits a net after an
152:
Does every convex polyhedron have a simple edge unfolding?
170:) so that the set of subdivided faces has a net. In 2014
90:
A Course in the Art of
Measurement with Compass and Ruler
104:. These constructions were first called nets in 1543 by
94:
Unterweysung der
Messung mit dem Zyrkel und Rychtscheyd
487:, so this claim should be regarded as unverified. See:
430:
Unterweysung der Messung mit dem Zyrkel und Rychtscheyd
1037:, Springer International Publishing, pp. 69–84,
321:
315:
can be found by representing these nets as a tree on
297:
1441:
1388:
1367:
1310:
1264:
1233:
1177:
571:(2007), "Chapter 22. Edge Unfolding of Polyhedra",
134:
and such that the sum of these defects is exactly 4
330:
303:
27:Edge-joined polygons which fold into a polyhedron
961:, Cambridge University Press, pp. 115–116,
73:which can be folded (along edges) to become the
1035:Imagine Math 3: Between Culture and Mathematics
291:The number of combinatorially distinct nets of
577:, Cambridge University Press, pp. 306–338
1155:
688:(1975), "Convex polytopes with convex nets",
8:
783:Notices of the American Mathematical Society
1162:
1148:
1140:
451:: CS1 maint: location missing publisher (
1007:
932:
878:
824:
794:
646:
435:. English translation with commentary in
320:
296:
166:convex polyhedron (for instance along a
984:(1 January 1998), "Dali's dimensions",
398:
270:, is used prominently in a painting by
156:(more unsolved problems in mathematics)
444:
920:Discrete & Computational Geometry
866:Discrete & Computational Geometry
559:
557:
495:Archive for History of Exact Sciences
61:is an arrangement of non-overlapping
7:
1397:Geometric Exercises in Paper Folding
216:path. For example, in the case of a
1418:A History of Folding in Mathematics
25:
282:"—And He Built a Crooked House—"
234:Higher-dimensional polytope nets
1318:Alexandrov's uniqueness theorem
277:Crucifixion (Corpus Hypercubus)
147:Unsolved problem in mathematics
140:Alexandrov's uniqueness theorem
763:Moskovich, D. (June 4, 2012),
224:The spider and the fly problem
1:
1256:Regular paperfolding sequence
598:American Mathematical Society
246:, one of the 261 nets of the
1404:Geometric Folding Algorithms
1171:Mathematics of paper folding
1107:Regular 4d Polytope Foldouts
413:, Cambridge University Press
261:, is composed of polyhedral
1043:10.1007/978-3-319-01231-5_7
437:Strauss, Walter L. (1977),
1591:
1454:Margherita Piazzola Beloch
1031:Henderson, Linda Dalrymple
889:10.1007/s00454-019-00082-1
527:Friedman, Michael (2018),
18:Shephard's conjecture
1225:Yoshizawa–Randlett system
1117:Paper Models of Polyhedra
955:O’Rourke, Joseph (2011),
934:10.1007/s00454-008-9052-3
710:10.1017/s0305004100051860
539:10.1007/978-3-319-72487-4
507:10.1007/s00407-008-0024-z
45:The eleven nets of a cube
1425:Origami Polyhedra Design
634:Graphs and Combinatorics
228:recreational mathematics
112:Existence and uniqueness
96:) included nets for the
843:10.2140/gt.2014.18.3055
744:"Shephard's Conjecture"
1215:Napkin folding problem
469:drew several nets for
332:
305:
250:
196:
121:
46:
38:
657:10.1007/s003730200005
333:
306:
257:, a four-dimensional
241:
188:
176:affine transformation
119:
44:
33:
1375:Fold-and-cut theorem
1331:Steffen's polyhedron
1195:Huzita–Hatori axioms
1185:Big-little-big lemma
765:"Dürer's conjecture"
588:Malkevitch, Joseph,
439:The Painter's Manual
407:Wenninger, Magnus J.
319:
295:
194:regular dodecahedron
106:Augustin Hirschvogel
36:regular dodecahedron
1323:Flexible polyhedron
1000:1998Natur.391...27K
835:2013arXiv1305.3231G
769:Open Problem Garden
702:1975MPCPS..78..389S
100:and several of the
1504:Toshikazu Kawasaki
1327:Bricard octahedron
1302:Yoshimura buckling
1200:Kawasaki's theorem
1090:Weisstein, Eric W.
1071:Weisstein, Eric W.
740:Weisstein, Eric W.
621:Demaine, Martin L.
489:Schreiber, Peter;
476:Divina proportione
372:Cardboard modeling
331:{\displaystyle 2n}
328:
301:
286:Robert A. Heinlein
251:
197:
122:
102:Archimedean solids
88:, whose 1525 book
47:
39:
1560:Types of polygons
1547:
1546:
1411:Geometric Origami
1282:Paper bag problem
1205:Maekawa's theorem
1052:978-3-319-01230-8
548:978-3-319-72486-7
467:Leonardo da Vinci
411:Polyhedron Models
304:{\displaystyle n}
16:(Redirected from
1582:
1484:David A. Huffman
1449:Roger C. Alperin
1352:Source unfolding
1220:Pureland origami
1164:
1157:
1150:
1141:
1103:
1102:
1084:
1083:
1056:
1055:
1027:
1021:
1020:
1011:
978:
972:
971:
952:
946:
945:
936:
927:(1–3): 339–388,
914:
908:
907:
882:
860:
854:
853:
828:
819:(5): 3055–3090,
806:
800:
799:
798:
796:10.1090/noti1609
778:
772:
771:
760:
754:
753:
752:
735:
729:
728:
682:
676:
675:
650:
629:O'Rourke, Joseph
617:Demaine, Erik D.
613:
607:
606:
605:
604:
585:
579:
578:
569:O'Rourke, Joseph
565:Demaine, Erik D.
561:
552:
551:
524:
518:
517:
483:nor in the 1498
463:
457:
456:
450:
442:
434:
421:
415:
414:
403:
356:
344:complement graph
340:perfect matching
337:
335:
334:
329:
310:
308:
307:
302:
148:
137:
21:
1590:
1589:
1585:
1584:
1583:
1581:
1580:
1579:
1550:
1549:
1548:
1543:
1529:Joseph O'Rourke
1464:Robert Connelly
1437:
1384:
1363:
1306:
1292:Schwarz lantern
1277:Modular origami
1260:
1229:
1173:
1168:
1088:
1087:
1069:
1068:
1065:
1060:
1059:
1053:
1029:
1028:
1024:
980:
979:
975:
969:
954:
953:
949:
916:
915:
911:
862:
861:
857:
808:
807:
803:
780:
779:
775:
762:
761:
757:
738:
737:
736:
732:
686:Shephard, G. C.
684:
683:
679:
615:
614:
610:
602:
600:
594:Feature Columns
587:
586:
582:
563:
562:
555:
549:
526:
525:
521:
491:Fischer, Gisela
488:
464:
460:
443:
436:
425:Dürer, Albrecht
423:
422:
418:
405:
404:
400:
395:
368:
352:
317:
316:
293:
292:
236:
209:
159:
158:
153:
150:
146:
135:
114:
98:Platonic solids
28:
23:
22:
15:
12:
11:
5:
1588:
1586:
1578:
1577:
1572:
1567:
1562:
1552:
1551:
1545:
1544:
1542:
1541:
1536:
1534:Tomohiro Tachi
1531:
1526:
1521:
1516:
1511:
1509:Robert J. Lang
1506:
1501:
1499:Humiaki Huzita
1496:
1491:
1486:
1481:
1479:Rona Gurkewitz
1476:
1474:Martin Demaine
1471:
1466:
1461:
1456:
1451:
1445:
1443:
1439:
1438:
1436:
1435:
1428:
1421:
1414:
1407:
1400:
1392:
1390:
1386:
1385:
1383:
1382:
1377:
1371:
1369:
1365:
1364:
1362:
1361:
1360:
1359:
1357:Star unfolding
1354:
1349:
1344:
1334:
1320:
1314:
1312:
1308:
1307:
1305:
1304:
1299:
1294:
1289:
1284:
1279:
1274:
1268:
1266:
1262:
1261:
1259:
1258:
1253:
1248:
1243:
1237:
1235:
1231:
1230:
1228:
1227:
1222:
1217:
1212:
1207:
1202:
1197:
1192:
1190:Crease pattern
1187:
1181:
1179:
1175:
1174:
1169:
1167:
1166:
1159:
1152:
1144:
1138:
1137:
1128:
1119:
1114:
1109:
1104:
1085:
1064:
1063:External links
1061:
1058:
1057:
1051:
1022:
973:
967:
947:
909:
873:(3): 671–689,
855:
801:
773:
755:
730:
696:(3): 389–403,
677:
608:
580:
553:
547:
519:
501:(4): 457–467,
458:
416:
397:
396:
394:
391:
390:
389:
384:
379:
374:
367:
364:
363:
362:
327:
324:
300:
235:
232:
208:
205:
172:Mohammad Ghomi
163:G. C. Shephard
154:
151:
145:
132:angular defect
113:
110:
86:Albrecht Dürer
79:solid geometry
26:
24:
14:
13:
10:
9:
6:
4:
3:
2:
1587:
1576:
1575:Spanning tree
1573:
1571:
1568:
1566:
1563:
1561:
1558:
1557:
1555:
1540:
1537:
1535:
1532:
1530:
1527:
1525:
1522:
1520:
1517:
1515:
1512:
1510:
1507:
1505:
1502:
1500:
1497:
1495:
1492:
1490:
1487:
1485:
1482:
1480:
1477:
1475:
1472:
1470:
1467:
1465:
1462:
1460:
1457:
1455:
1452:
1450:
1447:
1446:
1444:
1440:
1434:
1433:
1429:
1427:
1426:
1422:
1420:
1419:
1415:
1413:
1412:
1408:
1406:
1405:
1401:
1399:
1398:
1394:
1393:
1391:
1387:
1381:
1380:Lill's method
1378:
1376:
1373:
1372:
1370:
1368:Miscellaneous
1366:
1358:
1355:
1353:
1350:
1348:
1345:
1343:
1340:
1339:
1338:
1335:
1332:
1328:
1324:
1321:
1319:
1316:
1315:
1313:
1309:
1303:
1300:
1298:
1295:
1293:
1290:
1288:
1287:Rigid origami
1285:
1283:
1280:
1278:
1275:
1273:
1270:
1269:
1267:
1265:3d structures
1263:
1257:
1254:
1252:
1249:
1247:
1244:
1242:
1239:
1238:
1236:
1234:Strip folding
1232:
1226:
1223:
1221:
1218:
1216:
1213:
1211:
1208:
1206:
1203:
1201:
1198:
1196:
1193:
1191:
1188:
1186:
1183:
1182:
1180:
1176:
1172:
1165:
1160:
1158:
1153:
1151:
1146:
1145:
1142:
1136:
1132:
1129:
1127:
1123:
1120:
1118:
1115:
1113:
1110:
1108:
1105:
1101:
1100:
1095:
1091:
1086:
1082:
1081:
1076:
1072:
1067:
1066:
1062:
1054:
1048:
1044:
1040:
1036:
1032:
1026:
1023:
1019:
1015:
1010:
1009:10.1038/34063
1005:
1001:
997:
993:
989:
988:
983:
977:
974:
970:
968:9781139498548
964:
960:
959:
951:
948:
944:
940:
935:
930:
926:
922:
921:
913:
910:
906:
902:
898:
894:
890:
886:
881:
876:
872:
868:
867:
859:
856:
852:
848:
844:
840:
836:
832:
827:
822:
818:
814:
813:
805:
802:
797:
792:
788:
784:
777:
774:
770:
766:
759:
756:
751:
750:
745:
741:
734:
731:
727:
723:
719:
715:
711:
707:
703:
699:
695:
691:
687:
681:
678:
674:
670:
666:
662:
658:
654:
649:
648:cs.CG/0107024
644:
641:(1): 93–104,
640:
636:
635:
630:
626:
622:
618:
612:
609:
599:
595:
591:
584:
581:
576:
575:
570:
566:
560:
558:
554:
550:
544:
540:
536:
532:
531:
523:
520:
516:
512:
508:
504:
500:
496:
492:
486:
485:Geneva ms 210
482:
478:
477:
472:
468:
462:
459:
454:
448:
440:
432:
431:
426:
420:
417:
412:
408:
402:
399:
392:
388:
385:
383:
380:
378:
375:
373:
370:
369:
365:
360:
355:
350:
349:
348:
345:
341:
325:
322:
314:
311:-dimensional
298:
289:
287:
283:
279:
278:
273:
272:Salvador Dalí
269:
264:
260:
256:
249:
245:
240:
233:
231:
229:
225:
221:
219:
214:
213:shortest path
207:Shortest path
206:
204:
202:
195:
191:
187:
183:
181:
177:
173:
169:
164:
157:
143:
141:
133:
128:
127:spanning tree
118:
111:
109:
107:
103:
99:
95:
91:
87:
82:
80:
76:
72:
68:
64:
60:
56:
52:
43:
37:
32:
19:
1539:Eve Torrence
1469:Erik Demaine
1430:
1423:
1416:
1409:
1402:
1395:
1389:Publications
1336:
1251:Möbius strip
1241:Dragon curve
1178:Flat folding
1133:package for
1097:
1078:
1034:
1025:
994:(6662): 27,
991:
985:
982:Kemp, Martin
976:
957:
950:
924:
918:
912:
870:
864:
858:
816:
812:Geom. Topol.
810:
804:
789:(1): 25–27,
786:
782:
776:
768:
758:
747:
733:
693:
689:
680:
638:
632:
611:
601:, retrieved
593:
583:
573:
529:
522:
498:
494:
474:
471:Luca Pacioli
461:
438:
429:
419:
410:
401:
290:
275:
252:
222:
210:
198:
180:pseudo edges
179:
160:
123:
93:
89:
83:
54:
48:
1570:4-polytopes
1524:Kōryō Miura
1519:Jun Maekawa
1494:Kôdi Husimi
1210:Map folding
1135:Mathematica
1094:"Unfolding"
625:Lubiw, Anna
382:Paper model
253:A net of a
34:A net of a
1554:Categories
1514:Anna Lubiw
1347:Common net
1272:Miura fold
880:1709.04944
603:2014-05-14
441:, New York
393:References
387:UV mapping
377:Common net
313:hypercubes
255:4-polytope
244:Dalí cross
59:polyhedron
1565:Polyhedra
1432:Origamics
1311:Polyhedra
1131:Unfolding
1099:MathWorld
1080:MathWorld
897:0179-5376
826:1305.3231
749:MathWorld
726:122287769
268:hypercube
248:tesseract
168:cut locus
161:In 1975,
1489:Tom Hull
1459:Yan Chen
1342:Blooming
1246:Flexagon
1122:Unfolder
905:37547025
851:16827957
515:41134285
447:citation
427:(1525),
409:(1971),
366:See also
259:polytope
201:blooming
190:Blooming
67:polygons
65:-joined
51:geometry
1126:Blender
1018:5317132
996:Bibcode
943:2383765
831:Bibcode
718:0390915
698:Bibcode
665:1892436
357:in the
354:A091159
342:on the
69:in the
1442:People
1297:Sonobe
1049:
1016:
987:Nature
965:
941:
903:
895:
849:
724:
716:
671:
663:
545:
513:
1075:"Net"
1014:S2CID
901:S2CID
875:arXiv
847:S2CID
821:arXiv
722:S2CID
669:S2CID
643:arXiv
511:JSTOR
263:cells
226:is a
75:faces
71:plane
57:of a
1124:for
1047:ISBN
963:ISBN
893:ISSN
673:1489
543:ISBN
453:link
359:OEIS
242:The
218:cube
211:The
63:edge
53:, a
1337:Net
1039:doi
1004:doi
992:391
929:doi
885:doi
839:doi
791:doi
706:doi
653:doi
535:doi
503:doi
473:'s
284:by
55:net
49:In
1556::
1329:,
1096:,
1092:,
1077:,
1073:,
1045:,
1012:,
1002:,
990:,
939:MR
937:,
925:39
923:,
899:,
891:,
883:,
871:64
869:,
845:,
837:,
829:,
817:18
815:,
787:65
785:,
767:,
746:,
742:,
720:,
714:MR
712:,
704:,
694:78
692:,
667:,
661:MR
659:,
651:,
639:18
637:,
627:;
623:;
619:;
596:,
592:,
567:;
556:^
541:,
509:,
499:62
497:,
449:}}
445:{{
288:.
274:,
192:a
108:.
1333:)
1325:(
1163:e
1156:t
1149:v
1041::
1006::
998::
931::
887::
877::
841::
833::
823::
793::
708::
700::
655::
645::
537::
505::
455:)
361:)
326:n
323:2
299:n
149::
136:π
92:(
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.