1033:
609:
1028:{\displaystyle {\begin{aligned}w(x)={}&x^{20}-210x^{19}+20615x^{18}-1256850x^{17}+53327946x^{16}\\&{}-1672280820x^{15}+40171771630x^{14}-756111184500x^{13}\\&{}+11310276995381x^{12}-135585182899530x^{11}\\&{}+1307535010540395x^{10}-10142299865511450x^{9}\\&{}+63030812099294896x^{8}-311333643161390640x^{7}\\&{}+1206647803780373360x^{6}-3599979517947607200x^{5}\\&{}+8037811822645051776x^{4}-12870931245150988800x^{3}\\&{}+13803759753640704000x^{2}-8752948036761600000x\\&{}+2432902008176640000.\end{aligned}}}
1257:
38:
24:
1093:
1929:
1252:{\displaystyle {\begin{array}{rrrrr}1.00000&2.00000&3.00000&4.00000&5.00000\\6.00001&6.99970&8.00727&8.91725&20.84691\\10.09527\pm {}&11.79363\pm {}&13.99236\pm {}&16.73074\pm {}&19.50244\pm {}\\0.64350i&1.65233i&2.51883i&2.81262i&1.94033i\end{array}}}
2891:
2602:
1261:
Some of the roots are greatly displaced, even though the change to the coefficient is tiny and the original roots seem widely spaced. Wilkinson showed by the stability analysis discussed in the next section that this behavior is related to the fact that some roots
1752:
2096:| ≈ 0.000000119 is greater than the radius of convergence of the power series mentioned above (which is about 0.0000000029, somewhat smaller than the value 0.00000001 given by the crude estimate) so the linearized theory does not apply. For a value such as
2117:= 20 of Wilkinson's polynomial appear to be similar, as they are on opposite ends of a symmetric line of roots, and have the same set of distances 1, 2, 3, ..., 19 from other roots. However the analysis above shows that this is grossly misleading: the root
436:
It is therefore natural to expect that ill-conditioning also occurs when the polynomial has zeros which are very close. However, the problem may also be extremely ill-conditioned for polynomials with well-separated zeros. Wilkinson used the polynomial
1677:
1300:, so for numbers around 210, 2 was an error in the first bit position not represented in the computer. The two real numbers, −210 and −210 − 2, are represented by the same floating point number, which means that 2 is the
2310:
1492:
2696:
2460:
expresses the polynomial in a particular basis, namely that of the monomials. If the polynomial is expressed in another basis, then the problem of finding its roots may cease to be ill-conditioned. For example, in a
2468:
273:
594:
2364:
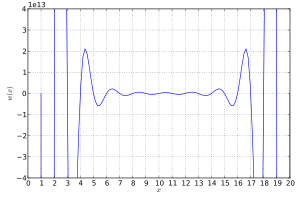
2689:
122:
1550:
614:
2092:
where the perturbed root has a large imaginary part but the first-order approximation (and for that matter all higher-order approximations) are real. The reason for this discrepancy is that |
361:
2458:
2146:
1391:
2922:. However, a perturbation in the other coefficients (all equal to zero) will slightly change the roots. Therefore, Wilkinson's polynomial is well-conditioned in this basis.
469:
and then finding its roots, since using the coefficients as an intermediate step may introduce an extreme ill-conditioning even if the original problem was well conditioned.
1924:{\displaystyle {d\alpha _{j} \over dt}=-{\alpha _{j}^{19} \over \prod _{k\neq j}(\alpha _{j}-\alpha _{k})}=-\prod _{k\neq j}{\alpha _{j} \over \alpha _{j}-\alpha _{k}}.\,\!}
2465:, a small change in one (or several) coefficients need not change the roots too much. Indeed, the basis polynomials for interpolation at the points 0, 1, 2, ..., 20 are
1304:
error in representing a real coefficient close to −210 by a floating point number on that computer. The perturbation analysis shows that 30-bit coefficient
2100:= 0.000000001 that is significantly smaller than this radius of convergence, the first-order approximation 19.9569... is reasonably close to the root 19.9509...
156:
480:
384:. That is, we hope that a small change in the coefficients will lead to a small change in the roots. Unfortunately, this is not the case here.
2315:
3017:
2950:
2609:
2886:{\displaystyle w(x)=(20!)\ell _{0}(x)=\sum _{i=0}^{20}d_{i}\ell _{i}(x)\quad {\text{with}}\quad d_{0}=(20!),\,d_{1}=d_{2}=\cdots =d_{20}=0.}
2044: = 20, the derivative is equal to −20/19! which is huge (about 43000000), so this root is very sensitive to small changes in
290:
2390:
3045:, ed. by G. H. Golub, pp. 1–28. (Studies in Mathematics, vol. 24). Washington, D.C.: Mathematical Association of America.
2597:{\displaystyle \ell _{k}(x)=\prod _{i=0,\ldots ,20 \atop i\neq k}{\frac {x-i}{k-i}},\qquad {\text{for}}\quad k=0,\ldots ,20.}
46:
150:
of a polynomial: the location of the roots can be very sensitive to perturbations in the coefficients of the polynomial.
2027:/19! ≈ 0.99999991779365). Similarly, the other small roots of Wilkinson's polynomial are insensitive to changes in
3039:
3074:
1098:
2023:
only changes from 1 to about 0.99999991779380 (which is very close to the first order approximation 1 +
466:
2312:
The twenty zeros of this polynomial are in a geometric progression with common ratio 2, and hence the quotient
1986: = 1, the derivative is equal to 1/19! which is very small; this root is stable even for large changes in
1672:{\displaystyle \alpha _{j}+{d\alpha _{j} \over dt}t+{d^{2}\alpha _{j} \over dt^{2}}{t^{2} \over 2!}+\cdots }
1683:| is larger than the radius of convergence of this power series, which is given by the smallest value of |
1305:
147:
2085:·20/19! = 25.137... to the perturbed root 20.84... is terrible; this is even more obvious for the root
3079:
456:
Speaking for myself I regard it as the most traumatic experience in my career as a numerical analyst.
387:
The problem is ill-conditioned when the polynomial has a multiple root. For instance, the polynomial
2462:
363:
It is a natural question in numerical analysis to ask whether the problem of finding the roots of
2938:
143:
131:
3013:
2946:
287:
Wilkinson's polynomial arose in the study of algorithms for finding the roots of a polynomial
2986:
J. H. Wilkinson (1959). The evaluation of the zeros of ill-conditioned polynomials. Part I.
2305:{\displaystyle w_{2}(x)=\prod _{i=1}^{20}(x-2^{-i})=(x-2^{-1})(x-2^{-2})\cdots (x-2^{-20}).}
381:
1500:, and conversely if this derivative is small the roots will be unstable. In particular, if
461:
Wilkinson's polynomial is often used to illustrate the undesirability of naively computing
37:
1487:{\displaystyle {d\alpha _{j} \over dt}=-{c(\alpha _{j}) \over p^{\prime }(\alpha _{j})}.}
1294:
3068:
3054:
1698:
becomes multiple. A very crude estimate for this radius takes half the distance from
279:
is also used to refer to some other polynomials appearing in
Wilkinson's discussion.
603:. These roots are far apart. However, the polynomial is still very ill-conditioned.
23:
1539:
1494:
When the derivative is large, the roots will be more stable under variations of
1297:
1045:(20) decreases from 0 to −220 = −6.25×10, and the root at
1388:. To first order, the change in the roots will be controlled by the derivative
1712:
In the example of
Wilkinson's polynomial of degree 20, the roots are given by
462:
139:
1290:
1090:
as the perturbation increases further. The 20 roots become (to 5 decimals)
1041:
is decreased from −210 by 2 to −210.0000001192, then the polynomial value
2606:
Every polynomial (of degree 20 or less) can be expressed in this basis:
1529:
happens to vanish there), and the roots will be extremely unstable.
1308:
is insufficient for separating the roots of
Wilkinson's polynomial.
268:{\displaystyle w(x)=\prod _{i=1}^{20}(x-i)=(x-1)(x-2)\cdots (x-20).}
3004:
It is mentioned in standard text books in numerical analysis, like
589:{\displaystyle w(x)=\prod _{i=1}^{20}(x-i)=(x-1)(x-2)\cdots (x-20)}
3028:
Ronald G. Mosier (July 1986). Root neighborhoods of a polynomial.
1511:
is a multiple root, then the denominator vanishes. In this case, α
465:
of a matrix by first calculating the coefficients of the matrix's
2081:= −2 the first-order approximation 20 −
2941:(1984). "The perfidious polynomial". In Gene H. Golub (ed.).
451:
In 1984, he described the personal impact of this discovery:
1457:
1709:
to the nearest root, and divides by the derivative above.
2359:{\displaystyle \alpha _{j} \over \alpha _{j}-\alpha _{k}}
3049:
A high-precision numerical computation is presented in:
2684:{\displaystyle p(x)=\sum _{i=0}^{20}d_{i}\ell _{i}(x).}
2895:
Given the definition of the
Lagrange basis polynomial
1080:
which turns into a pair of complex conjugate roots at
117:{\displaystyle \operatorname {sgn}(w(x))\ln(1+|w(x)|)}
2699:
2612:
2471:
2393:
2319:
2149:
1755:
1553:
1394:
1096:
612:
483:
293:
159:
49:
2945:. Mathematical Association of America. p. 3.
2885:
2683:
2596:
2452:
2358:
2304:
2131:= 1 (to small perturbations in the coefficient of
1923:
1671:
1486:
1289:Wilkinson chose the perturbation of 2 because his
1251:
1027:
588:
355:
267:
116:
2135:) by a factor of 20 = 5242880000000000000000000.
1920:
3000:. Englewood Cliffs, New Jersey: Prentice Hall.
356:{\displaystyle p(x)=\sum _{i=0}^{n}c_{i}x^{i}.}
2453:{\displaystyle p(x)=\sum _{i=0}^{n}c_{i}x^{i}}
2143:The second example considered by Wilkinson is
1517:is usually not differentiable with respect to
8:
1940:will be less stable if there are many roots
1994:are a long way from it, in the sense that |
448:to illustrate this point (Wilkinson 1963).
2871:
2852:
2839:
2834:
2810:
2800:
2784:
2774:
2764:
2753:
2731:
2698:
2663:
2653:
2643:
2632:
2611:
2567:
2537:
2498:
2476:
2470:
2444:
2434:
2424:
2413:
2392:
2349:
2336:
2324:
2317:
2287:
2259:
2234:
2206:
2187:
2176:
2154:
2148:
1919:
1907:
1894:
1883:
1877:
1865:
1843:
1830:
1811:
1800:
1795:
1789:
1766:
1756:
1754:
1647:
1641:
1632:
1617:
1607:
1600:
1577:
1567:
1558:
1552:
1469:
1456:
1441:
1428:
1405:
1395:
1393:
1201:
1191:
1181:
1171:
1161:
1097:
1095:
1013:
991:
979:
966:
950:
938:
925:
909:
897:
884:
868:
856:
843:
827:
815:
802:
786:
774:
761:
745:
729:
717:
704:
688:
672:
656:
640:
632:
613:
611:
514:
503:
482:
344:
334:
324:
313:
292:
190:
179:
158:
106:
89:
48:
3061:(for Python), retrieved on 29 July 2006.
2982:Wilkinson discussed "his" polynomial in
2966:Trefethen, Lloyd N.; Bau, David (1997),
146:in 1963 to illustrate a difficulty when
2930:
2916:will produce no change in the roots of
2998:Rounding Errors in Algebraic Processes
2366:cannot be large. Indeed, the zeros of
2016:is as large as –10000000000, the root
1990:. This is because all the other roots
473:Conditioning of Wilkinson's polynomial
2005:| = 1, 2, 3, ..., 19 is larger than |
1377:, and ask how this affects the roots
1316:Suppose that we perturb a polynomial
7:
2693:For Wilkinson's polynomial, we find
1274:that are "close" in the sense that |
606:Expanding the polynomial, one finds
2070:| = 1, 2, 3, ..., 19 is less than |
1958:, in the sense that the distance |α
1538:the perturbed root is given by the
3055:Polynomials And Rational Functions
2499:
2037:. On the other hand, for the root
14:
2012:| = 1. For example, even if
1970:| between them is smaller than |α
596:clearly has 20 roots, located at
1749:. So the derivative is given by
36:
22:
2805:
2799:
2572:
2566:
1679:and one expects problems when |
2907:, a change in the coefficient
2828:
2819:
2796:
2790:
2743:
2737:
2724:
2715:
2709:
2703:
2675:
2669:
2622:
2616:
2488:
2482:
2403:
2397:
2296:
2274:
2268:
2246:
2243:
2221:
2215:
2193:
2166:
2160:
2138:
1849:
1823:
1475:
1462:
1447:
1434:
1073:collide into a double root at
626:
620:
583:
571:
565:
553:
550:
538:
532:
520:
493:
487:
303:
297:
259:
247:
241:
229:
226:
214:
208:
196:
169:
163:
111:
107:
103:
97:
90:
80:
71:
68:
62:
56:
29:Plot of Wilkinson's polynomial
1:
3043:Studies in Numerical Analysis
2943:Studies in Numerical Analysis
2379:changes in the coefficients.
410:(a perturbation of size
1270: = 15) have many roots
421:, which is much bigger than
3010:Numerical methods that work
1351:by adding a small multiple
3096:
3059:RPN Calculator User Manual
3040:The perfidious polynomial.
3030:Mathematics of Computation
2375:are quite stable to large
2139:Wilkinson's second example
472:
400:. However, the polynomial
393:has a double root at
2124:= 20 is less stable than
2103:At first sight the roots
1931:This shows that the root
467:characteristic polynomial
3038:J. H. Wilkinson (1984).
2996:J. H. Wilkinson (1963).
2968:Numerical Linear Algebra
1282:| is smaller than |
2383:The effect of the basis
477:Wilkinson's polynomial
2887:
2769:
2685:
2648:
2598:
2454:
2429:
2360:
2306:
2192:
1925:
1673:
1488:
1253:
1037:If the coefficient of
1029:
590:
519:
459:
369:from the coefficients
357:
329:
277:Wilkinson's polynomial
269:
195:
136:Wilkinson's polynomial
118:
2988:Numerische Mathematik
2888:
2749:
2686:
2628:
2599:
2455:
2409:
2361:
2307:
2172:
2059:, in the sense that |
1926:
1687:| such that the root
1674:
1489:
1254:
1030:
591:
499:
453:
358:
309:
270:
175:
119:
2697:
2610:
2469:
2391:
2316:
2147:
1964: − α
1753:
1551:
1532:For small values of
1392:
1293:computer had 30-bit
1094:
1019:2432902008176640000.
985:13803759753640704000
960:12870931245150988800
610:
481:
291:
275:Sometimes, the term
157:
47:
2939:Wilkinson, James H.
2063: −
2001: −
1805:
1001:8752948036761600000
944:8037811822645051776
919:3599979517947607200
903:1206647803780373360
3075:Numerical analysis
3024:Other references:
2883:
2681:
2594:
2536:
2450:
2330:
2302:
2048:. The other roots
1921:
1876:
1822:
1791:
1669:
1484:
1312:Stability analysis
1249:
1247:
1025:
1023:
878:311333643161390640
586:
353:
265:
153:The polynomial is
144:James H. Wilkinson
142:which was used by
132:numerical analysis
114:
3018:978-0-88385-450-1
2952:978-0-88385-126-5
2803:
2570:
2561:
2534:
2494:
2356:
1914:
1861:
1853:
1807:
1781:
1661:
1639:
1592:
1479:
1420:
862:63030812099294896
837:10142299865511450
3087:
2972:
2971:
2963:
2957:
2956:
2935:
2921:
2915:
2906:
2892:
2890:
2889:
2884:
2876:
2875:
2857:
2856:
2844:
2843:
2815:
2814:
2804:
2801:
2789:
2788:
2779:
2778:
2768:
2763:
2736:
2735:
2690:
2688:
2687:
2682:
2668:
2667:
2658:
2657:
2647:
2642:
2603:
2601:
2600:
2595:
2571:
2568:
2562:
2560:
2549:
2538:
2535:
2533:
2522:
2481:
2480:
2459:
2457:
2456:
2451:
2449:
2448:
2439:
2438:
2428:
2423:
2374:
2365:
2363:
2362:
2357:
2355:
2354:
2353:
2341:
2340:
2329:
2328:
2318:
2311:
2309:
2308:
2303:
2295:
2294:
2267:
2266:
2242:
2241:
2214:
2213:
2191:
2186:
2159:
2158:
1982:. For the root α
1957:
1948:
1939:
1930:
1928:
1927:
1922:
1915:
1913:
1912:
1911:
1899:
1898:
1888:
1887:
1878:
1875:
1854:
1852:
1848:
1847:
1835:
1834:
1821:
1804:
1799:
1790:
1782:
1780:
1772:
1771:
1770:
1757:
1744:
1733:
1726:
1708:
1697:
1678:
1676:
1675:
1670:
1662:
1660:
1652:
1651:
1642:
1640:
1638:
1637:
1636:
1623:
1622:
1621:
1612:
1611:
1601:
1593:
1591:
1583:
1582:
1581:
1568:
1563:
1562:
1547:
1537:
1528:
1522:
1510:
1499:
1493:
1491:
1490:
1485:
1480:
1478:
1474:
1473:
1461:
1460:
1450:
1446:
1445:
1429:
1421:
1419:
1411:
1410:
1409:
1396:
1387:
1376:
1366:of a polynomial
1365:
1350:
1339:
1258:
1256:
1255:
1250:
1248:
1202:
1192:
1182:
1172:
1162:
1089:
1079:
1072:
1065:
1058:
1051:
1034:
1032:
1031:
1026:
1024:
1014:
1009:
996:
995:
980:
975:
971:
970:
955:
954:
939:
934:
930:
929:
914:
913:
898:
893:
889:
888:
873:
872:
857:
852:
848:
847:
832:
831:
821:1307535010540395
816:
811:
807:
806:
791:
790:
775:
770:
766:
765:
750:
749:
734:
733:
718:
713:
709:
708:
693:
692:
677:
676:
661:
660:
645:
644:
633:
602:
595:
593:
592:
587:
518:
513:
447:
432:
426:
420:
409:
399:
392:
382:well-conditioned
379:
368:
362:
360:
359:
354:
349:
348:
339:
338:
328:
323:
274:
272:
271:
266:
194:
189:
148:finding the root
123:
121:
120:
115:
110:
93:
40:
26:
3095:
3094:
3090:
3089:
3088:
3086:
3085:
3084:
3065:
3064:
2980:
2975:
2965:
2964:
2960:
2953:
2937:
2936:
2932:
2928:
2917:
2914:
2908:
2900:
2896:
2867:
2848:
2835:
2806:
2780:
2770:
2727:
2695:
2694:
2659:
2649:
2608:
2607:
2550:
2539:
2523:
2500:
2472:
2467:
2466:
2440:
2430:
2389:
2388:
2385:
2373:
2367:
2345:
2332:
2331:
2320:
2314:
2313:
2283:
2255:
2230:
2202:
2150:
2145:
2144:
2141:
2130:
2123:
2116:
2109:
2091:
2076:
2069:
2058:
2043:
2022:
2011:
2000:
1985:
1975:
1969:
1963:
1956:
1950:
1947:
1941:
1938:
1932:
1903:
1890:
1889:
1879:
1839:
1826:
1806:
1773:
1762:
1758:
1751:
1750:
1735:
1728:
1721:
1713:
1707:
1699:
1696:
1688:
1653:
1643:
1628:
1624:
1613:
1603:
1602:
1584:
1573:
1569:
1554:
1549:
1548:
1543:
1533:
1524:
1518:
1516:
1509:
1501:
1495:
1465:
1452:
1451:
1437:
1430:
1412:
1401:
1397:
1390:
1389:
1386:
1378:
1367:
1352:
1349:
1341:
1337:
1317:
1314:
1246:
1245:
1237:
1229:
1221:
1213:
1204:
1203:
1193:
1183:
1173:
1163:
1152:
1151:
1146:
1141:
1136:
1131:
1125:
1124:
1119:
1114:
1109:
1104:
1092:
1091:
1081:
1074:
1067:
1060:
1059:. The roots at
1053:
1046:
1022:
1021:
1007:
1006:
987:
973:
972:
962:
946:
932:
931:
921:
905:
891:
890:
880:
864:
850:
849:
839:
823:
809:
808:
798:
796:135585182899530
782:
768:
767:
757:
741:
725:
711:
710:
700:
684:
668:
652:
636:
634:
608:
607:
601:= 1, 2, ..., 20
597:
479:
478:
475:
438:
428:
422:
415:
414:) has roots at
401:
394:
388:
378:
370:
364:
340:
330:
289:
288:
285:
155:
154:
128:
127:
126:
125:
124:
45:
44:
41:
32:
31:
30:
27:
12:
11:
5:
3093:
3091:
3083:
3082:
3077:
3067:
3066:
3063:
3062:
3057:, part of the
3047:
3046:
3036:
3035:(175):265–273.
3022:
3021:
3020:, p. 201.
3002:
3001:
2994:
2979:
2976:
2974:
2973:
2958:
2951:
2929:
2927:
2924:
2912:
2898:
2882:
2879:
2874:
2870:
2866:
2863:
2860:
2855:
2851:
2847:
2842:
2838:
2833:
2830:
2827:
2824:
2821:
2818:
2813:
2809:
2798:
2795:
2792:
2787:
2783:
2777:
2773:
2767:
2762:
2759:
2756:
2752:
2748:
2745:
2742:
2739:
2734:
2730:
2726:
2723:
2720:
2717:
2714:
2711:
2708:
2705:
2702:
2680:
2677:
2674:
2671:
2666:
2662:
2656:
2652:
2646:
2641:
2638:
2635:
2631:
2627:
2624:
2621:
2618:
2615:
2593:
2590:
2587:
2584:
2581:
2578:
2575:
2565:
2559:
2556:
2553:
2548:
2545:
2542:
2532:
2529:
2526:
2521:
2518:
2515:
2512:
2509:
2506:
2503:
2497:
2493:
2490:
2487:
2484:
2479:
2475:
2447:
2443:
2437:
2433:
2427:
2422:
2419:
2416:
2412:
2408:
2405:
2402:
2399:
2396:
2387:The expansion
2384:
2381:
2371:
2352:
2348:
2344:
2339:
2335:
2327:
2323:
2301:
2298:
2293:
2290:
2286:
2282:
2279:
2276:
2273:
2270:
2265:
2262:
2258:
2254:
2251:
2248:
2245:
2240:
2237:
2233:
2229:
2226:
2223:
2220:
2217:
2212:
2209:
2205:
2201:
2198:
2195:
2190:
2185:
2182:
2179:
2175:
2171:
2168:
2165:
2162:
2157:
2153:
2140:
2137:
2128:
2121:
2114:
2107:
2089:
2074:
2067:
2056:
2041:
2020:
2009:
1998:
1983:
1971:
1965:
1959:
1952:
1943:
1934:
1918:
1910:
1906:
1902:
1897:
1893:
1886:
1882:
1874:
1871:
1868:
1864:
1860:
1857:
1851:
1846:
1842:
1838:
1833:
1829:
1825:
1820:
1817:
1814:
1810:
1803:
1798:
1794:
1788:
1785:
1779:
1776:
1769:
1765:
1761:
1717:
1703:
1692:
1668:
1665:
1659:
1656:
1650:
1646:
1635:
1631:
1627:
1620:
1616:
1610:
1606:
1599:
1596:
1590:
1587:
1580:
1576:
1572:
1566:
1561:
1557:
1512:
1505:
1483:
1477:
1472:
1468:
1464:
1459:
1455:
1449:
1444:
1440:
1436:
1433:
1427:
1424:
1418:
1415:
1408:
1404:
1400:
1382:
1345:
1333:
1313:
1310:
1295:floating point
1244:
1241:
1238:
1236:
1233:
1230:
1228:
1225:
1222:
1220:
1217:
1214:
1212:
1209:
1206:
1205:
1200:
1197:
1194:
1190:
1187:
1184:
1180:
1177:
1174:
1170:
1167:
1164:
1160:
1157:
1154:
1153:
1150:
1147:
1145:
1142:
1140:
1137:
1135:
1132:
1130:
1127:
1126:
1123:
1120:
1118:
1115:
1113:
1110:
1108:
1105:
1103:
1100:
1099:
1020:
1017:
1012:
1010:
1008:
1005:
1002:
999:
994:
990:
986:
983:
978:
976:
974:
969:
965:
961:
958:
953:
949:
945:
942:
937:
935:
933:
928:
924:
920:
917:
912:
908:
904:
901:
896:
894:
892:
887:
883:
879:
876:
871:
867:
863:
860:
855:
853:
851:
846:
842:
838:
835:
830:
826:
822:
819:
814:
812:
810:
805:
801:
797:
794:
789:
785:
781:
780:11310276995381
778:
773:
771:
769:
764:
760:
756:
753:
748:
744:
740:
737:
732:
728:
724:
721:
716:
714:
712:
707:
703:
699:
696:
691:
687:
683:
680:
675:
671:
667:
664:
659:
655:
651:
648:
643:
639:
635:
631:
628:
625:
622:
619:
616:
615:
585:
582:
579:
576:
573:
570:
567:
564:
561:
558:
555:
552:
549:
546:
543:
540:
537:
534:
531:
528:
525:
522:
517:
512:
509:
506:
502:
498:
495:
492:
489:
486:
474:
471:
374:
352:
347:
343:
337:
333:
327:
322:
319:
316:
312:
308:
305:
302:
299:
296:
284:
281:
264:
261:
258:
255:
252:
249:
246:
243:
240:
237:
234:
231:
228:
225:
222:
219:
216:
213:
210:
207:
204:
201:
198:
193:
188:
185:
182:
178:
174:
171:
168:
165:
162:
138:is a specific
113:
109:
105:
102:
99:
96:
92:
88:
85:
82:
79:
76:
73:
70:
67:
64:
61:
58:
55:
52:
42:
35:
34:
33:
28:
21:
20:
19:
18:
17:
13:
10:
9:
6:
4:
3:
2:
3092:
3081:
3078:
3076:
3073:
3072:
3070:
3060:
3056:
3052:
3051:
3050:
3044:
3041:
3037:
3034:
3031:
3027:
3026:
3025:
3019:
3015:
3011:
3008:F. S. Acton,
3007:
3006:
3005:
2999:
2995:
2992:
2989:
2985:
2984:
2983:
2977:
2969:
2962:
2959:
2954:
2948:
2944:
2940:
2934:
2931:
2925:
2923:
2920:
2911:
2904:
2893:
2880:
2877:
2872:
2868:
2864:
2861:
2858:
2853:
2849:
2845:
2840:
2836:
2831:
2825:
2822:
2816:
2811:
2807:
2793:
2785:
2781:
2775:
2771:
2765:
2760:
2757:
2754:
2750:
2746:
2740:
2732:
2728:
2721:
2718:
2712:
2706:
2700:
2691:
2678:
2672:
2664:
2660:
2654:
2650:
2644:
2639:
2636:
2633:
2629:
2625:
2619:
2613:
2604:
2591:
2588:
2585:
2582:
2579:
2576:
2573:
2563:
2557:
2554:
2551:
2546:
2543:
2540:
2530:
2527:
2524:
2519:
2516:
2513:
2510:
2507:
2504:
2501:
2495:
2491:
2485:
2477:
2473:
2464:
2463:Lagrange form
2445:
2441:
2435:
2431:
2425:
2420:
2417:
2414:
2410:
2406:
2400:
2394:
2382:
2380:
2378:
2370:
2350:
2346:
2342:
2337:
2333:
2325:
2321:
2299:
2291:
2288:
2284:
2280:
2277:
2271:
2263:
2260:
2256:
2252:
2249:
2238:
2235:
2231:
2227:
2224:
2218:
2210:
2207:
2203:
2199:
2196:
2188:
2183:
2180:
2177:
2173:
2169:
2163:
2155:
2151:
2136:
2134:
2127:
2120:
2113:
2106:
2101:
2099:
2095:
2088:
2084:
2080:
2073:
2066:
2062:
2055:
2052:are close to
2051:
2047:
2040:
2036:
2032:
2030:
2026:
2019:
2015:
2008:
2004:
1997:
1993:
1989:
1981:
1977:
1974:
1968:
1962:
1955:
1946:
1937:
1916:
1908:
1904:
1900:
1895:
1891:
1884:
1880:
1872:
1869:
1866:
1862:
1858:
1855:
1844:
1840:
1836:
1831:
1827:
1818:
1815:
1812:
1808:
1801:
1796:
1792:
1786:
1783:
1777:
1774:
1767:
1763:
1759:
1748:
1742:
1738:
1731:
1725:
1720:
1716:
1710:
1706:
1702:
1695:
1691:
1686:
1682:
1666:
1663:
1657:
1654:
1648:
1644:
1633:
1629:
1625:
1618:
1614:
1608:
1604:
1597:
1594:
1588:
1585:
1578:
1574:
1570:
1564:
1559:
1555:
1546:
1542:expansion in
1541:
1536:
1530:
1527:
1521:
1515:
1508:
1504:
1498:
1481:
1470:
1466:
1453:
1442:
1438:
1431:
1425:
1422:
1416:
1413:
1406:
1402:
1398:
1385:
1381:
1374:
1370:
1363:
1359:
1355:
1348:
1344:
1336:
1332:
1328:
1324:
1320:
1311:
1309:
1307:
1303:
1299:
1296:
1292:
1287:
1285:
1281:
1278: −
1277:
1273:
1269:
1265:
1259:
1242:
1239:
1234:
1231:
1226:
1223:
1218:
1215:
1210:
1207:
1198:
1195:
1188:
1185:
1178:
1175:
1168:
1165:
1158:
1155:
1148:
1143:
1138:
1133:
1128:
1121:
1116:
1111:
1106:
1101:
1088:
1084:
1077:
1070:
1063:
1056:
1049:
1044:
1040:
1035:
1018:
1015:
1011:
1003:
1000:
997:
992:
988:
984:
981:
977:
967:
963:
959:
956:
951:
947:
943:
940:
936:
926:
922:
918:
915:
910:
906:
902:
899:
895:
885:
881:
877:
874:
869:
865:
861:
858:
854:
844:
840:
836:
833:
828:
824:
820:
817:
813:
803:
799:
795:
792:
787:
783:
779:
776:
772:
762:
758:
754:
751:
746:
742:
738:
735:
730:
726:
722:
719:
715:
705:
701:
697:
694:
689:
685:
681:
678:
673:
669:
665:
662:
657:
653:
649:
646:
641:
637:
629:
623:
617:
604:
600:
580:
577:
574:
568:
562:
559:
556:
547:
544:
541:
535:
529:
526:
523:
515:
510:
507:
504:
500:
496:
490:
484:
470:
468:
464:
458:
457:
452:
449:
445:
441:
434:
431:
425:
419:
413:
408:
404:
397:
391:
385:
383:
377:
373:
367:
350:
345:
341:
335:
331:
325:
320:
317:
314:
310:
306:
300:
294:
282:
280:
278:
262:
256:
253:
250:
244:
238:
235:
232:
223:
220:
217:
211:
205:
202:
199:
191:
186:
183:
180:
176:
172:
166:
160:
151:
149:
145:
141:
137:
133:
100:
94:
86:
83:
77:
74:
65:
59:
53:
50:
39:
25:
16:
3058:
3048:
3042:
3032:
3029:
3023:
3009:
3003:
2997:
2990:
2987:
2981:
2967:
2961:
2942:
2933:
2918:
2909:
2902:
2894:
2692:
2605:
2386:
2376:
2368:
2142:
2132:
2125:
2118:
2111:
2104:
2102:
2097:
2093:
2086:
2082:
2078:
2077:| = 20. For
2071:
2064:
2060:
2053:
2049:
2045:
2038:
2034:
2033:
2028:
2024:
2017:
2013:
2006:
2002:
1995:
1991:
1987:
1979:
1978:
1972:
1966:
1960:
1953:
1944:
1935:
1746:
1745:is equal to
1740:
1736:
1732:= 1, ..., 20
1729:
1723:
1718:
1714:
1711:
1704:
1700:
1693:
1689:
1684:
1680:
1544:
1540:power series
1534:
1531:
1525:
1519:
1513:
1506:
1502:
1496:
1383:
1379:
1372:
1368:
1361:
1357:
1353:
1346:
1342:
1334:
1330:
1326:
1322:
1318:
1315:
1301:
1298:significands
1288:
1283:
1279:
1275:
1271:
1267:
1263:
1260:
1086:
1085:≈ 19.5 ± 1.9
1082:
1075:
1068:
1061:
1054:
1047:
1042:
1038:
1036:
755:756111184500
605:
598:
476:
460:
455:
454:
450:
443:
439:
435:
429:
423:
417:
411:
406:
402:
395:
389:
386:
375:
371:
365:
286:
276:
152:
135:
129:
15:
3080:Polynomials
3053:Ray Buvel,
1340:with roots
1302:unavoidable
739:40171771630
463:eigenvalues
3069:Categories
2978:References
723:1672280820
433:is small.
283:Background
140:polynomial
2993::150–166.
2862:⋯
2782:ℓ
2751:∑
2729:ℓ
2661:ℓ
2630:∑
2586:…
2555:−
2544:−
2528:≠
2514:…
2496:∏
2474:ℓ
2411:∑
2347:α
2343:−
2334:α
2322:α
2289:−
2281:−
2272:⋯
2261:−
2253:−
2236:−
2228:−
2208:−
2200:−
2174:∏
1949:close to
1905:α
1901:−
1892:α
1881:α
1870:≠
1863:∏
1859:−
1841:α
1837:−
1828:α
1816:≠
1809:∏
1793:α
1787:−
1764:α
1667:⋯
1615:α
1575:α
1556:α
1467:α
1458:′
1439:α
1426:−
1403:α
1306:precision
1291:Pilot ACE
1266:(such as
1199:±
1189:±
1179:±
1169:±
1159:±
1052:grows to
998:−
957:−
916:−
875:−
834:−
793:−
752:−
720:−
679:−
647:−
578:−
569:⋯
560:−
545:−
527:−
501:∏
311:∑
254:−
245:⋯
236:−
221:−
203:−
177:∏
78:
54:
2377:relative
2110:= 1 and
1523:(unless
1329:−
1196:19.50244
1186:16.73074
1176:13.99236
1166:11.79363
1156:10.09527
1149:20.84691
698:53327946
405:−
43:Plot of
2035:Example
1980:Example
1325:) = Π (
1240:1.94033
1232:2.81262
1224:2.51883
1216:1.65233
1208:0.64350
1144:8.91725
1139:8.00727
1134:6.99970
1129:6.00001
1122:5.00000
1117:4.00000
1112:3.00000
1107:2.00000
1102:1.00000
1078:≈ 18.62
682:1256850
3016:
2970:, SIAM
2949:
1734:, and
1057:≈ 20.8
2926:Notes
666:20615
427:when
3014:ISBN
2947:ISBN
2802:with
1727:for
1071:= 19
1066:and
1064:= 18
1050:= 20
2592:20.
2569:for
1976:|.
1286:|.
650:210
398:= 0
380:is
130:In
51:sgn
3071::
3033:47
3012:,
2881:0.
2873:20
2823:20
2766:20
2719:20
2645:20
2520:20
2292:20
2189:20
2122:20
2115:20
2090:19
2075:20
2068:20
2057:20
2042:20
2031:.
1802:19
1722:=
829:10
804:11
788:12
763:13
747:14
731:15
706:16
690:17
674:18
658:19
642:20
581:20
516:20
416:±√
257:20
192:20
134:,
75:ln
2991:1
2955:.
2919:w
2913:0
2910:d
2905:)
2903:x
2901:(
2899:0
2897:ℓ
2878:=
2869:d
2865:=
2859:=
2854:2
2850:d
2846:=
2841:1
2837:d
2832:,
2829:)
2826:!
2820:(
2817:=
2812:0
2808:d
2797:)
2794:x
2791:(
2786:i
2776:i
2772:d
2761:0
2758:=
2755:i
2747:=
2744:)
2741:x
2738:(
2733:0
2725:)
2722:!
2716:(
2713:=
2710:)
2707:x
2704:(
2701:w
2679:.
2676:)
2673:x
2670:(
2665:i
2655:i
2651:d
2640:0
2637:=
2634:i
2626:=
2623:)
2620:x
2617:(
2614:p
2589:,
2583:,
2580:0
2577:=
2574:k
2564:,
2558:i
2552:k
2547:i
2541:x
2531:k
2525:i
2517:,
2511:,
2508:0
2505:=
2502:i
2492:=
2489:)
2486:x
2483:(
2478:k
2446:i
2442:x
2436:i
2432:c
2426:n
2421:0
2418:=
2415:i
2407:=
2404:)
2401:x
2398:(
2395:p
2372:2
2369:w
2351:k
2338:j
2326:j
2300:.
2297:)
2285:2
2278:x
2275:(
2269:)
2264:2
2257:2
2250:x
2247:(
2244:)
2239:1
2232:2
2225:x
2222:(
2219:=
2216:)
2211:i
2204:2
2197:x
2194:(
2184:1
2181:=
2178:i
2170:=
2167:)
2164:x
2161:(
2156:2
2152:w
2133:x
2129:1
2126:α
2119:α
2112:α
2108:1
2105:α
2098:t
2094:t
2087:α
2083:t
2079:t
2072:α
2065:α
2061:β
2054:α
2050:β
2046:t
2039:α
2029:t
2025:t
2021:1
2018:α
2014:t
2010:1
2007:α
2003:β
1999:1
1996:α
1992:β
1988:t
1984:1
1973:j
1967:k
1961:j
1954:j
1951:α
1945:k
1942:α
1936:j
1933:α
1917:.
1909:k
1896:j
1885:j
1873:j
1867:k
1856:=
1850:)
1845:k
1832:j
1824:(
1819:j
1813:k
1797:j
1784:=
1778:t
1775:d
1768:j
1760:d
1747:x
1743:)
1741:x
1739:(
1737:c
1730:j
1724:j
1719:j
1715:α
1705:j
1701:α
1694:j
1690:α
1685:t
1681:t
1664:+
1658:!
1655:2
1649:2
1645:t
1634:2
1630:t
1626:d
1619:j
1609:2
1605:d
1598:+
1595:t
1589:t
1586:d
1579:j
1571:d
1565:+
1560:j
1545:t
1535:t
1526:c
1520:t
1514:j
1507:j
1503:α
1497:t
1482:.
1476:)
1471:j
1463:(
1454:p
1448:)
1443:j
1435:(
1432:c
1423:=
1417:t
1414:d
1407:j
1399:d
1384:j
1380:α
1375:)
1373:x
1371:(
1369:c
1364:)
1362:x
1360:(
1358:c
1356:·
1354:t
1347:j
1343:α
1338:)
1335:j
1331:α
1327:x
1323:x
1321:(
1319:p
1284:α
1280:β
1276:α
1272:β
1268:α
1264:α
1243:i
1235:i
1227:i
1219:i
1211:i
1087:i
1083:x
1076:x
1069:x
1062:x
1055:x
1048:x
1043:w
1039:x
1016:+
1004:x
993:2
989:x
982:+
968:3
964:x
952:4
948:x
941:+
927:5
923:x
911:6
907:x
900:+
886:7
882:x
870:8
866:x
859:+
845:9
841:x
825:x
818:+
800:x
784:x
777:+
759:x
743:x
736:+
727:x
702:x
695:+
686:x
670:x
663:+
654:x
638:x
630:=
627:)
624:x
621:(
618:w
599:x
584:)
575:x
572:(
566:)
563:2
557:x
554:(
551:)
548:1
542:x
539:(
536:=
533:)
530:i
524:x
521:(
511:1
508:=
505:i
497:=
494:)
491:x
488:(
485:w
446:)
444:x
442:(
440:w
430:ε
424:ε
418:ε
412:ε
407:ε
403:x
396:x
390:x
376:i
372:c
366:p
351:.
346:i
342:x
336:i
332:c
326:n
321:0
318:=
315:i
307:=
304:)
301:x
298:(
295:p
263:.
260:)
251:x
248:(
242:)
239:2
233:x
230:(
227:)
224:1
218:x
215:(
212:=
209:)
206:i
200:x
197:(
187:1
184:=
181:i
173:=
170:)
167:x
164:(
161:w
112:)
108:|
104:)
101:x
98:(
95:w
91:|
87:+
84:1
81:(
72:)
69:)
66:x
63:(
60:w
57:(
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.