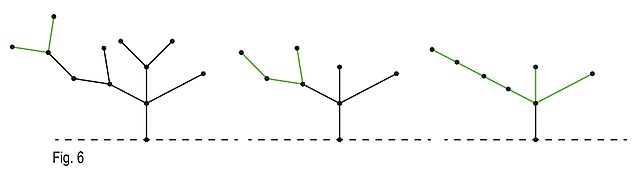
237:. This principle changes the representation of the game to the more basic version of the bamboo stalks. The last possible set of graphs that can be made are convergent ones, also known as arbitrarily rooted graphs. By using the fusion principle, we can state that all vertices on any cycle may be fused together without changing the value of the graph. Therefore, any convergent graph can also be interpreted as a simple bamboo stalk graph. By combining all three types of graphs we can add complexity to the game, without ever changing the nim sum of the game, thereby allowing the game to take the strategies of Nim.
477:
93:
38:
224:
In the impartial version of
Hackenbush (the one without player specified colors), it can be thought of using nim heaps by breaking the game up into several cases: vertical, convergent, and divergent. Played exclusively with vertical stacks of line segments, also referred to as bamboo stalks, the game
83:
assumption that the game can be finished in a finite amount of time, provided that there are only finitely many line segments directly "touching" the ground. On an infinite board, based on the layout of the board the game can continue on forever, assuming there are infinitely many points touching
64:
The game starts with the players drawing a "ground" line (conventionally, but not necessarily, a horizontal line at the bottom of the paper or other playing area) and several line segments such that each line segment is connected to the ground, either directly at an endpoint, or indirectly, via a
135:: Each line segment is colored either red or blue. One player (usually the first, or left, player) is only allowed to cut blue line segments, while the other player (usually the second, or right, player) is only allowed to cut red line segments.
126:
All line segments are the same color and may be cut by either player. This means payoffs are symmetric and each player has the same operations based on position on board (in this case structure of drawing). This is also called Green
117:, meaning that the options (moves) available to one player would not necessarily be the ones available to the other player if it were their turn to move given the same position. This is achieved in one of two ways:
220:
to each vertex that lies on the ground (which should be considered as a distinguished vertex — it does no harm to identify all the ground points together — rather than as a line on the graph).
147:
Blue-Red
Hackenbush is merely a special case of Blue-Red-Green Hackenbush, but it is worth noting separately, as its analysis is often much simpler. This is because Blue-Red Hackenbush is a so-called
245:
The Colon
Principle states that when branches come together at a vertex, one may replace the branches by a non-branching stalk of length equal to their nim sum. Consider a fixed but arbitrary graph,
143:: Each line segment is colored red, blue, or green. The rules are the same as for Blue-Red Hackenbush, with the additional stipulation that green line segments can be cut by either player.
79:
many (in the case of a "finite board") or infinitely many (in the case of an "infinite board") line segments. The existence of an infinite number of line segments does not violate the
68:
On their turn, a player "cuts" (erases) any line segment of their choice. Every line segment no longer connected to the ground by any path "falls" (i.e., gets erased). According to the
596:
193:, and many more general values that are neither. Blue-Red-Green Hackenbush allows for the construction of additional games whose values are not real numbers, such as
470:
that keeps the
Sprague-Grundy values the same. In this way you will always have a reply to every move he may make. This means you will make the last move and so win.
364:
have the same
Sprague-Grundy value is equivalent to the claim that the sum of the two games has Sprague-Grundy value 0. In other words, we are to show that the sum
476:
173:
98:
527:
65:
chain of other segments connected by endpoints. Any number of segments may meet at a point and thus there may be multiple paths to ground.
675:
233:
stating that when branches come together at a vertex, one may replace the branches by a non-branching stalk of length equal to their
572:
539:
670:
229:
and can be directly analyzed as such. Divergent segments, or trees, add an additional wrinkle to the game and require use of the
680:
645:
685:
665:
110:
534:. Mathematical Sciences Research Institute Publications. Vol. 29. Cambridge University Press. pp. 61–78.
162:
80:
31:
614:
69:
209:
532:
Games of No Chance: Papers from the
Combinatorial Games Workshop held in Berkeley, CA, July 11–21, 1994
631:
167:
105:
In the original folklore version of
Hackenbush, any player is allowed to cut any edge: as this is an
161:
Hackenbush has often been used as an example game for demonstrating the definitions and concepts in
217:
213:
177:
by some of the founders of the field. In particular Blue-Red
Hackenbush can be used to construct
610:
590:
194:
49:
271:
be arbitrary trees (or graphs) that have the same
Sprague-Grundy value. Consider the two graphs
578:
568:
535:
567:. Conway, John H. (John Horton), Guy, Richard K. (2nd ed.). Natick, Mass.: A.K. Peters.
113:. Thus the versions of Hackenbush of interest in combinatorial game theory are more complex
549:
545:
182:
378:
is a P-position. A player is guaranteed to win if they are the second player to move in
350:
have the same
Sprague-Grundy value. Consider the sum of the two games. The claim that
190:
178:
106:
153:, which means, essentially, that it can never be an advantage to have the first move.
659:
114:
205:
53:
186:
92:
76:
37:
17:
582:
502:
149:
72:
of combinatorial game theory, the first player who is unable to move loses.
109:
it is comparatively straightforward to give a complete analysis using the
482:
An instance in which the game can be reduced using the Colon Principle
185:, while the values of infinite Blue-Red Hackenbush boards account for
428:
are not disturbed.) If the first player moves by chopping an edge in
234:
198:
56:
connected to one another by their endpoints and to a "ground" line.
396:
in one of the games, then the second player chops the same edge in
650:
91:
36:
226:
392:. If the first player moves by chopping one of the edges in
30:
For the Groucho Marx character, Hugo Z. Hackenbush, see
327:
represents the graph constructed by attaching the tree
456:
are no longer equal, so that there exists a move in
400:
in the other game. (Such a pair of moves may delete
181:: finite Blue-Red Hackenbush boards can construct
96:A blue-red Hackenbush girl, introduced in the book
52:. It may be played on any configuration of colored
342:. The colon principle states that the two graphs
204:Further analysis of the game can be made using
48:is a two-player game invented by mathematician
8:
595:: CS1 maint: multiple names: authors list (
208:by considering the board as a collection of
41:A starting setup for the game of Hackenbush
565:Winning ways for your mathematical plays
174:Winning Ways for Your Mathematical Plays
99:Winning Ways for your Mathematical Plays
493:
472:
588:
165:, beginning with its use in the books
7:
651:Hackenbush on Pencil and Paper Games
442:, then the Sprague-Grundy values of
530:. In Nowakowski, Richard J. (ed.).
563:R., Berlekamp, Elwyn (2001–2004).
249:, and select an arbitrary vertex,
25:
646:Hackenstrings, and 0.999... vs. 1
75:Hackenbush boards can consist of
635:, 2nd edition, A K Peters, 2000.
475:
27:Mathematical pen-and-paper game
414:from the games, but otherwise
1:
702:
29:
676:Combinatorial game theory
163:combinatorial game theory
140:Blue-Red-Green Hackenbush
32:A Day at the Races (film)
526:Guy, Richard K. (1996).
241:Proof of Colon Principle
671:Abstract strategy games
183:dyadic rational numbers
681:Paper-and-pencil games
111:Sprague–Grundy theorem
102:
70:normal play convention
42:
503:"What is Hackenbush?"
95:
40:
632:On Numbers and Games
168:On Numbers and Games
123:Original Hackenbush:
611:Ferguson, Thomas S.
132:Blue-Red Hackenbush
686:John Horton Conway
666:Mathematical games
216:and examining the
103:
50:John Horton Conway
43:
528:"Impartial games"
225:directly becomes
16:(Redirected from
693:
629:John H. Conway,
622:
621:
619:
607:
601:
600:
594:
586:
560:
554:
553:
523:
517:
516:
514:
513:
498:
479:
21:
701:
700:
696:
695:
694:
692:
691:
690:
656:
655:
642:
626:
625:
617:
609:
608:
604:
587:
575:
562:
561:
557:
542:
525:
524:
520:
511:
509:
500:
499:
495:
490:
483:
480:
468:
461:
454:
447:
440:
433:
426:
419:
412:
405:
390:
383:
376:
369:
362:
355:
332:
325:
318:
311:
304:
297:
290:
283:
276:
269:
262:
243:
231:colon principle
179:surreal numbers
159:
90:
62:
35:
28:
23:
22:
15:
12:
11:
5:
699:
697:
689:
688:
683:
678:
673:
668:
658:
657:
654:
653:
648:
641:
640:External links
638:
637:
636:
624:
623:
602:
573:
555:
540:
518:
492:
491:
489:
486:
485:
484:
481:
474:
466:
459:
452:
445:
438:
431:
424:
417:
410:
403:
388:
381:
374:
367:
360:
353:
334:to the vertex
330:
323:
316:
309:
302:
295:
288:
281:
274:
267:
260:
242:
239:
197:and all other
158:
155:
145:
144:
136:
128:
115:partisan games
107:impartial game
89:
86:
61:
58:
26:
24:
14:
13:
10:
9:
6:
4:
3:
2:
698:
687:
684:
682:
679:
677:
674:
672:
669:
667:
664:
663:
661:
652:
649:
647:
644:
643:
639:
634:
633:
628:
627:
616:
615:"Game Theory"
613:(Fall 2000).
612:
606:
603:
598:
592:
584:
580:
576:
574:9781568811420
570:
566:
559:
556:
551:
547:
543:
541:0-521-57411-0
537:
533:
529:
522:
519:
508:
504:
497:
494:
487:
478:
473:
471:
469:
462:
455:
448:
441:
434:
427:
420:
413:
406:
399:
395:
391:
384:
377:
370:
363:
356:
349:
345:
341:
338:of the graph
337:
333:
326:
319:
312:
305:
298:
291:
284:
277:
270:
263:
256:
252:
248:
240:
238:
236:
232:
228:
222:
219:
215:
211:
207:
202:
200:
196:
192:
188:
184:
180:
176:
175:
170:
169:
164:
156:
154:
152:
151:
142:
141:
137:
134:
133:
129:
125:
124:
120:
119:
118:
116:
112:
108:
101:
100:
94:
87:
85:
82:
78:
73:
71:
66:
59:
57:
55:
54:line segments
51:
47:
39:
33:
19:
18:Hackenstrings
630:
605:
564:
558:
531:
521:
510:. Retrieved
507:geometer.org
506:
501:Davis, Tom.
496:
464:
457:
450:
443:
436:
429:
422:
415:
408:
401:
397:
393:
386:
379:
372:
365:
358:
351:
347:
343:
339:
335:
328:
321:
314:
307:
300:
293:
286:
279:
272:
265:
258:
254:
250:
246:
244:
230:
223:
206:graph theory
203:
187:real numbers
172:
166:
160:
148:
146:
139:
138:
131:
130:
122:
121:
104:
97:
84:the ground.
74:
67:
63:
45:
44:
127:Hackenbush.
81:game theory
660:Categories
512:2023-02-12
488:References
46:Hackenbush
591:cite book
150:cold game
583:45102937
320: :
313:, where
306: :
285: :
210:vertices
191:ordinals
157:Analysis
88:Variants
77:finitely
60:Gameplay
550:1427953
235:nim sum
199:nimbers
581:
571:
548:
538:
257:. Let
618:(PDF)
253:, in
218:paths
214:edges
597:link
579:OCLC
569:ISBN
536:ISBN
449:and
421:and
407:and
357:and
346:and
292:and
264:and
212:and
195:star
171:and
463:or
435:or
227:Nim
662::
593:}}
589:{{
577:.
546:MR
544:.
505:.
385:+
371:+
348:G2
344:G1
299:=
278:=
201:.
189:,
620:.
599:)
585:.
552:.
515:.
467:2
465:H
460:1
458:H
453:2
451:H
446:1
444:H
439:2
437:H
432:1
430:H
425:2
423:H
418:1
416:H
411:2
409:H
404:1
402:H
398:G
394:G
389:2
387:G
382:1
380:G
375:2
373:G
368:1
366:G
361:2
359:G
354:1
352:G
340:G
336:x
331:i
329:H
324:i
322:H
317:x
315:G
310:2
308:H
303:x
301:G
296:2
294:G
289:1
287:H
282:x
280:G
275:1
273:G
268:2
266:H
261:1
259:H
255:G
251:x
247:G
34:.
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.