58:
419:: a decomposition into triangles such that each edge on a triangle is glued to at most one other edge. Each triangle is oriented by choosing a direction around the perimeter of the triangle, associating a direction to each edge of the triangle. If this is done in such a way that, when glued together, neighboring edges are pointing in the opposite direction, then this determines an orientation of the surface. Such a choice is only possible if the surface is orientable, and in this case there are exactly two different orientations.
3559:
3342:
3580:
3548:
3617:
3590:
3570:
236:) is orientable if a consistent concept of clockwise rotation can be defined on the surface in a continuous manner. That is to say that a loop going around one way on the surface can never be continuously deformed (without overlapping itself) to a loop going around the opposite way. This turns out to be equivalent to the question of whether the surface contains no subset that is
425:
217:
140:
223:
149:
46:
852:
At the heart of all the above definitions of orientability of a differentiable manifold is the notion of an orientation preserving transition function. This raises the question of what exactly such transition functions are preserving. They cannot be preserving an orientation of the manifold because
2670:
manifold is space orientable if, whenever two right-handed observers head off in rocket ships starting at the same spacetime point, and then meet again at another point, they remain right-handed with respect to one another. If a spacetime is time-orientable then the two observers will always agree
2415:
428:
can be consistently positioned at all points of the surface without turning into its mirror image, then this will induce an orientation in the above sense on each of the triangles of the triangulation by selecting the direction of each of the triangles based on the order red-green-blue of colors of
326:
Note that locally an embedded surface always has two sides, so a near-sighted ant crawling on a one-sided surface would think there is an "other side". The essence of one-sidedness is that the ant can crawl from one side of the surface to the "other" without going through the surface or flipping
188:
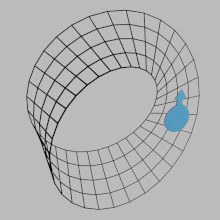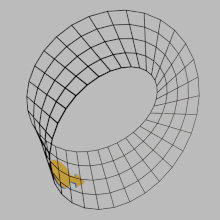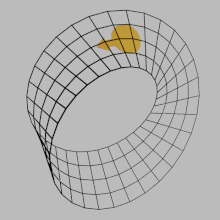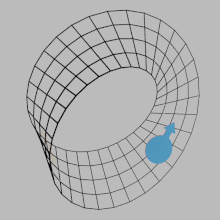
In this animation, a simple analogy is made using a gear that rotates according to the right-hand rule on a surface's normal vector. The orientation of the curves given by the boundaries is given by the direction in which the dots move as they are pushed by the moving gear. On a non-orientable
74:
860:
corresponds to a choice of left and right near that point. On a two-dimensional manifold, it corresponds to a choice of clockwise and counter-clockwise. These two situations share the common feature that they are described in terms of top-dimensional behavior near
282:
surface is subtle and frequently blurred. An orientable surface is an abstract surface that admits an orientation, while an oriented surface is a surface that is abstractly orientable, and has the additional datum of a choice of one of the two possible orientations.
2509:
Another way to construct this cover is to divide the loops based at a basepoint into either orientation-preserving or orientation-reversing loops. The orientation preserving loops generate a subgroup of the fundamental group which is either the whole group or of
2186:
185:
2082:
824:. A transition function is orientation preserving if and only if it sends right-handed bases to right-handed bases. The existence of a volume form implies a reduction of the structure group of the tangent bundle or the frame bundle to
2514:
two. In the latter case (which means there is an orientation-reversing path), the subgroup corresponds to a connected double covering; this cover is orientable by construction. In the former case, one can simply take two copies of
2422:
2420:
2417:
2416:
2421:
1230:
2951:
2777:
2868:
959:
1496:
1384:
1114:
1048:
159:
Various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds often employ methods of
2419:
710:
of positive determinant matrices, or equivalently if there exists an atlas whose transition functions determine an orientation preserving linear transformation on each tangent space, then the manifold
1307:
698:. That is, the transition functions of the manifold induce transition functions on the tangent bundle which are fiberwise linear transformations. If the structure group can be reduced to the group
1629:
pushes forward to the fixed generator. Conversely, an oriented atlas determines such a generator as compatible local orientations can be glued together to give a generator for the homology group
1760:
1962:
2094:
2671:
on the direction of time at both points of their meeting. In fact, a spacetime is time-orientable if and only if any two observers can agree which of the two meetings preceded the other.
1827:
1671:
1623:
1563:
844:
is orientable, then local volume forms can be patched together to create a global volume form, orientability being necessary to ensure that the global form is nowhere vanishing.
375:
1502:
is related to the first chart by an orientation preserving transition function, and this implies that the two charts yield the same generator, whence the generator is unique.
1979:
2603:
853:
an orientation of the manifold is an atlas, and it makes no sense to say that a transition function preserves or does not preserve an atlas of which it is a member.
4475:
405:
3666:
3620:
2617:, this reduction is always possible if the underlying base manifold is orientable and in fact this provides a convenient way to define the orientability of a
4470:
718:
is orientable if and only if the structure group of the tangent bundle can be reduced in this way. Similar observations can be made for the frame bundle.
3757:
2418:
3781:
3976:
315:
are non-orientable. They, as visualized in 3-dimensions, all have just one side. The real projective plane and Klein bottle cannot be embedded in
3123:
172:. A generalization of the notion of orientability of a space is that of orientability of a family of spaces parameterized by some other space (a
1160:
3150:
3846:
3019:
176:) for which an orientation must be selected in each of the spaces which varies continuously with respect to changes in the parameter values.
4072:
2883:
2704:
2803:
4125:
3653:
895:
2394:
is positively oriented if and only if it, when combined with the inward pointing normal vector, defines a positively oriented basis of
1435:
1323:
1053:
987:
330:
In general, the property of being orientable is not equivalent to being two-sided; however, this holds when the ambient space (such as
4409:
3254:
3051:
3226:
2790:
is the determinant, which gives the orientation character. A space-orientation of a pseudo-Riemannian manifold is identified with a
3608:
3603:
3133:
3099:
4174:
2563:
856:
This question can be resolved by defining local orientations. On a one-dimensional manifold, a local orientation around a point
3766:
4157:
3598:
3219:
1245:
4518:
2528:
1830:
4369:
3500:
3158:
117:
if such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is an
1691:
4354:
4077:
3851:
2181:{\displaystyle \{{\text{Image of }}\alpha {\text{ in }}H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)\colon p\in U\}}
1911:
39:
4399:
3119:
189:
surface, such as the Möbius strip, the boundary would have to move in both directions at once, which is not possible.
30:"Orientation (mathematics)" and "Orientation (space)" redirect here. For the orientation of a shape in a space, see
4404:
4374:
4082:
4038:
4019:
3786:
3730:
3508:
3091:
3043:
1309:, so the geometric significance of the choice of generator is that it distinguishes charts from their reflections.
35:
2877:) is the bundle of pseudo-orthogonal frames. Similarly, a time orientation is a section of the associated bundle
1686:
3941:
3806:
259:. For surfaces embedded in Euclidean space, an orientation is specified by the choice of a continuously varying
1885:. The set of local orientations can therefore be given a topology, and this topology makes it into a manifold.
775:
is an oriented atlas. The existence of a volume form is therefore equivalent to orientability of the manifold.
4326:
4191:
3883:
3725:
3579:
3307:
1581:
of this group. This generator determines an oriented atlas by fixing a generator of the infinite cyclic group
416:
274:. More generally, an orientable surface admits exactly two orientations, and the distinction between an orient
165:
675:
Orientability and orientations can also be expressed in terms of the tangent bundle. The tangent bundle is a
436:-manifold having a triangulation. However, some 4-manifolds do not have a triangulation, and in general for
220:) cannot be moved around the surface and back to where it started so that it looks like its own mirror image (
1780:
1232:. A choice of generator therefore corresponds to a decision of whether, in the given chart, a sphere around
247:
For an orientable surface, a consistent choice of "clockwise" (as opposed to counter-clockwise) is called an
4023:
3993:
3917:
3907:
3863:
3693:
3646:
3593:
3083:
2675:
320:
211:
3791:
1849:
there are two local orientations. Intuitively, there is a way to move from a local orientation at a point
1632:
1584:
1524:
4364:
3983:
3878:
3698:
3528:
3523:
3449:
3326:
3314:
3287:
3247:
3177:
2791:
569:
464:
31:
2987:
2651:
4013:
4008:
3370:
3297:
2655:
308:
3558:
2077:{\displaystyle H_{n}(M,M\setminus U;\mathbf {Z} )\to H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}
778:
Volume forms and tangent vectors can be combined to give yet another description of orientability. If
340:
4344:
4282:
4130:
3834:
3824:
3796:
3771:
3681:
3518:
3470:
3444:
3292:
2629:
is orientable (as a vector bundle). Note that as a manifold in its own right, the tangent bundle is
2606:
616:
3182:
4482:
4455:
4164:
4042:
4027:
3956:
3715:
3569:
3365:
2647:
2511:
2084:. The codomain of this group has two generators, and α maps to one of them. The topology on
1150:
296:
4424:
4379:
4276:
4147:
3951:
3776:
3639:
3563:
3513:
3434:
3424:
3302:
3282:
3167:
2663:
2281:
is defined to be an orientation of its interior. Such an orientation induces an orientation of ∂
506:
106:
66:
3961:
3533:
57:
2569:
244:. Thus, for surfaces, the Möbius strip may be considered the source of all non-orientability.
4523:
4359:
4339:
4334:
4241:
4152:
3966:
3946:
3801:
3740:
3551:
3417:
3375:
3240:
3129:
3095:
3047:
3015:
2967:
2962:
2795:
2471:
1154:
266:
at every point. If such a normal exists at all, then there are always two ways to select it:
169:
98:
94:
4497:
4291:
4246:
4169:
4140:
3998:
3931:
3926:
3921:
3911:
3703:
3686:
3331:
3277:
3187:
3079:
2687:
2659:
1829:
parametrizes the choices of orientations. This characterization of orientability extends to
981:
487:
3207:
2470:
is either smooth so we can choose an orientation on the tangent space at a point or we use
1424:
at each point. This is made precise by noting that any chart in the oriented atlas around
383:
73:
4440:
4349:
4179:
4135:
3901:
3390:
3385:
3115:
2618:
2559:
2551:
684:
198:
161:
134:
130:
102:
2427:
304:
241:
153:
62:
607:
be a differentiable manifold. This means that the transition functions in the atlas of
4306:
4231:
4201:
4099:
4092:
4032:
4003:
3873:
3868:
3829:
3480:
3412:
3213:
3003:
2626:
2614:
2435:
1386:. From here, the relevant definitions are the same as in the differentiable case. An
545:
260:
3191:
587:
must be made into a special case. When more than one of these definitions applies to
4512:
4492:
4316:
4311:
4296:
4286:
4236:
4213:
4087:
4047:
3936:
3735:
3400:
3380:
3035:
3011:
2540:
676:
595:
is orientable under one definition if and only if it is orientable under the others.
78:
3583:
1120:
is contractible, so its homology groups vanish except in degree zero, and the space
619:. When the Jacobian determinant is positive, the transition function is said to be
4419:
4414:
4256:
4223:
4196:
4104:
3745:
3475:
3395:
3341:
680:
312:
237:
184:
173:
144:
113:
that allows a consistent definition of "clockwise" and "anticlockwise". A space is
4262:
4251:
4208:
4109:
3710:
3573:
3485:
2610:
2534:
2478:
we consider the corresponding set of pairs and define that to be an open set of
722:
86:
4487:
4445:
4271:
4184:
3816:
3720:
3429:
3360:
3319:
380:
can be one-sided, and a Klein bottle in the same space can be two-sided; here
129:
if "clockwise" is changed into "counterclockwise" after running through some
27:
Possibility of a consistent definition of "clockwise" in a mathematical space
4301:
4266:
3971:
3858:
3454:
2667:
631:
is an atlas for which all transition functions are orientation preserving.
721:
Another way to define orientations on a differentiable manifold is through
1225:{\displaystyle H_{n-1}\left(S^{n-1};\mathbf {Z} \right)\cong \mathbf {Z} }
17:
4465:
4460:
4450:
3841:
3662:
3439:
3407:
3356:
3263:
2622:
233:
110:
3172:
2229:
mentioned above are homeomorphic to the disjoint union of two copies of
771:
for which the standard volume form pulls back to a positive multiple of
3631:
2368:
is described by the inward pointing normal vector. The orientation of
1766:/2 coefficients is zero, then the manifold is orientable. Moreover, if
964:
To see the geometric significance of this group, choose a chart around
2310:, is in the chosen oriented atlas. The restriction of this chart to ∂
2225:
is even a local homeomorphism, because the preimages of the open sets
1390:
is one for which all transition functions are orientation preserving,
424:
216:
139:
4057:
292:
122:
2946:{\displaystyle \operatorname {O} (M)\times _{\sigma _{-}}\{-1,+1\}.}
2772:{\displaystyle \sigma _{\pm }:\operatorname {O} (p,q)\to \{-1,+1\}.}
143:, that moves continuously along such a loop is changed into its own
2863:{\displaystyle \operatorname {O} (M)\times _{\sigma _{+}}\{-1,+1\}}
2548:
2494:
is then a 2-to-1 covering map. This covering space is called the
2413:
954:{\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right).}
300:
183:
72:
56:
50:
44:
1872:, that coordinate chart defines compatible local orientations at
1505:
Purely homological definitions are also possible. Assuming that
1491:{\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}
1379:{\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}
1109:{\displaystyle H_{n}\left(B,B\setminus \{O\};\mathbf {Z} \right)}
1043:{\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}
291:
Most surfaces encountered in the physical world are orientable.
2474:
to define orientation. Then for every open, oriented subset of
222:
148:
133:
in it, and coming back to the starting point. This means that a
45:
3635:
3236:
580:
has extra structure, like being differentiable. Occasionally,
572:. There are several possible definitions of what it means for
1968:. Assume that α is a generator of this group. For each
168:
more structure is present, allowing a formulation in terms of
1762:
vanishes. In particular, if the first cohomology group with
3232:
3220:
Orientation of manifolds in generalized cohomology theories
576:
to be orientable. Some of these definitions require that
1138:-sphere, so its homology groups vanish except in degrees
2519:, each of which corresponds to a different orientation.
1302:{\displaystyle H_{n-1}\left(S^{n-1};\mathbf {Z} \right)}
334:
above) is orientable. For example, a torus embedded in
121:
of the space. Real vector spaces, Euclidean spaces, and
2625:: a smooth manifold is defined to be orientable if its
1862:: when the two points lie in the same coordinate chart
444:-manifolds have triangulations that are inequivalent.
2886:
2806:
2707:
2572:
2097:
1982:
1914:
1783:
1694:
1635:
1625:
and taking the oriented charts to be those for which
1587:
1527:
1438:
1326:
1248:
1163:
1157:
shows that the above homology group is isomorphic to
1056:
990:
898:
386:
343:
2277:
is a manifold with boundary, then an orientation of
1312:
On a topological manifold, a transition function is
739:, the top exterior power of the cotangent bundle of
429:
any of the figures in the interior of the triangle.
4433:
4392:
4325:
4222:
4118:
4065:
4056:
3892:
3815:
3754:
3674:
3499:
3463:
3349:
3270:
1755:{\displaystyle w_{1}(M)\in H^{1}(M;\mathbf {Z} /2)}
848:
Homology and the orientability of general manifolds
2945:
2862:
2771:
2597:
2180:
2076:
1957:{\displaystyle H_{n}(M,M\setminus U;\mathbf {Z} )}
1956:
1821:
1754:
1665:
1617:
1557:
1490:
1378:
1301:
1224:
1108:
1042:
953:
399:
369:
1900:we will specify a subbase for its topology. Let
327:over an edge, but simply by crawling far enough.
2426:Animation of the orientable double cover of the
836:. As before, this implies the orientability of
725:. A volume form is a nowhere vanishing section
232:. An abstract surface (i.e., a two-dimensional
2633:orientable, even over nonorientable manifolds.
1420:ought to define a unique local orientation of
3647:
3248:
544:factor is generated by the middle curve in a
34:. For the orientation of a vector space, see
8:
2937:
2919:
2857:
2839:
2763:
2745:
2381:is defined by the condition that a basis of
2175:
2147:
2141:
2098:
2058:
2052:
1472:
1466:
1432:, and this sphere determines a generator of
1360:
1354:
1090:
1084:
1024:
1018:
968:. In that chart there is a neighborhood of
932:
926:
603:The most intuitive definitions require that
3225:The Encyclopedia of Mathematics article on
2337:, the restriction of the tangent bundle of
2318:. Such charts form an oriented atlas for ∂
2257:is connected and orientable. The manifold
4062:
3654:
3640:
3632:
3616:
3589:
3255:
3241:
3233:
2434:A closely related notion uses the idea of
2306:which, when restricted to the interior of
2285:. Indeed, suppose that an orientation of
1320:in its domain, it fixes the generators of
1236:is positive or negative. A reflection of
65:is a non-orientable surface. Note how the
3181:
3171:
2911:
2906:
2885:
2831:
2826:
2805:
2712:
2706:
2694:and the time orientation character σ
2580:
2571:
2153:
2118:
2109:
2101:
2096:
2064:
2029:
2014:
1987:
1981:
1946:
1919:
1913:
1855:to a local orientation at a nearby point
1808:
1803:
1788:
1782:
1741:
1736:
1721:
1699:
1693:
1655:
1640:
1634:
1607:
1592:
1586:
1547:
1532:
1526:
1478:
1443:
1437:
1428:can be used to determine a sphere around
1398:if it admits an oriented atlas, and when
1366:
1331:
1325:
1289:
1274:
1253:
1247:
1217:
1204:
1189:
1168:
1162:
1096:
1061:
1055:
1030:
995:
989:
938:
903:
897:
796:is a basis of tangent vectors at a point
599:Orientability of differentiable manifolds
391:
385:
361:
348:
342:
156:is an example of a non-orientable space.
2690:: the space orientation character σ
2650:, there are two kinds of orientability:
1892:be the set of all local orientations of
3125:The Large Scale Structure of Space-Time
3066:
2978:
2782:Their product σ = σ
2486:a topology and the projection sending (
2245:is the disjoint union of two copies of
2138:
2049:
2005:
1937:
1831:orientability of general vector bundles
1822:{\displaystyle H^{0}(M;\mathbf {Z} /2)}
1685:is orientable if and only if the first
1463:
1351:
1242:through the origin acts by negation on
1081:
1015:
923:
889:is a choice of generator of the group
639:if it admits an oriented atlas. When
615:-functions. Such a function admits a
2241:itself is one of these open sets, so
1666:{\displaystyle H_{n}(M;\mathbf {Z} )}
1618:{\displaystyle H_{n}(M;\mathbf {Z} )}
1558:{\displaystyle H_{n}(M;\mathbf {Z} )}
214:two-dimensional figure (for example,
7:
1498:. Moreover, any other chart around
747:has a standard volume form given by
654:is a maximal oriented atlas. (When
2213:. It is clear that every point of
2887:
2807:
2721:
2302:be a chart at a boundary point of
2217:has precisely two preimages under
2205:that sends a local orientation at
1976:, there is a pushforward function
303:are orientable, for example. But
25:
2662:of spacetime. In the context of
2253:is non-orientable, however, then
432:This approach generalizes to any
370:{\displaystyle K^{2}\times S^{1}}
3615:
3588:
3578:
3568:
3557:
3547:
3546:
3340:
3151:"The Orientability of Spacetime"
2989:Modern multidimensional calculus
2154:
2065:
2015:
1947:
1804:
1737:
1656:
1608:
1548:
1479:
1367:
1290:
1218:
1205:
1097:
1031:
939:
423:
221:
215:
147:
138:
2986:Munroe, Marshall Evans (1963).
1837:, not just the tangent bundle.
1416:Intuitively, an orientation of
800:, then the basis is said to be
761:, the collection of all charts
3694:Differentiable/Smooth manifold
3128:. Cambridge University Press.
2992:. Addison-Wesley. p. 263.
2899:
2893:
2819:
2813:
2742:
2739:
2727:
2592:
2586:
2529:Orientation of a vector bundle
2022:
2019:
1993:
1951:
1925:
1816:
1794:
1749:
1727:
1711:
1705:
1660:
1646:
1612:
1598:
1565:is isomorphic to the integers
1552:
1538:
1:
3159:Classical and Quantum Gravity
3069:, p. 236 Theorem 3.26(a)
2523:Orientation of vector bundles
1413:is a maximal oriented atlas.
869:. For the general case, let
475:is orientable if and only if
2658:. These play a role in the
2502:is connected if and only if
1841:The orientation double cover
714:is orientable. Conversely,
411:Orientation by triangulation
407:refers to the Klein bottle.
253:, and the surface is called
226:). Otherwise the surface is
40:Orientation (disambiguation)
4400:Classification of manifolds
3192:10.1088/0264-9381/19/17/308
2438:. For a connected manifold
564:be a connected topological
125:are orientable. A space is
4540:
3509:Banach fixed-point theorem
3094:. p. 79 Theorem 1.2.
3092:Princeton University Press
3044:Cambridge University Press
2532:
2526:
1677:Orientation and cohomology
1149:. A computation with the
757:. Given a volume form on
556:Orientability of manifolds
467:group of a closed surface
448:Orientability and homology
36:Orientation (vector space)
29:
4476:over commutative algebras
3542:
3338:
2598:{\displaystyle GL^{+}(n)}
2329:is smooth, at each point
2194:There is a canonical map
1577:is a choice of generator
1509:is closed and connected,
536:is free abelian, and the
323:with nice intersections.
4192:Riemann curvature tensor
3208:Orientation of manifolds
3149:Hadley, Mark J. (2002).
3084:Michelsohn, Marie-Louise
2498:, as it is orientable.
2263:orientation double cover
166:differentiable manifolds
53:is an orientable surface
2676:pseudo-orthogonal group
2496:orientable double cover
2410:Orientable double cover
2269:Manifolds with boundary
3984:Manifold with boundary
3699:Differential structure
3564:Mathematics portal
3464:Metrics and properties
3450:Second-countable space
3222:at the Manifold Atlas.
3216:at the Manifold Atlas.
3210:at the Manifold Atlas.
2947:
2864:
2773:
2599:
2431:
2364:, where the factor of
2182:
2078:
1958:
1823:
1756:
1667:
1619:
1559:
1492:
1380:
1314:orientation preserving
1303:
1226:
1110:
1044:
972:which is an open ball
955:
621:orientation preserving
401:
371:
309:real projective planes
190:
93:is a property of some
82:
70:
69:flips with every loop.
54:
38:. For other uses, see
32:Orientation (geometry)
4519:Differential topology
3008:Calculus on Manifolds
2948:
2865:
2774:
2600:
2462:is an orientation at
2425:
2183:
2079:
1959:
1904:be an open subset of
1845:Around each point of
1824:
1757:
1687:Stiefel–Whitney class
1668:
1620:
1560:
1493:
1381:
1304:
1227:
1111:
1045:
956:
490:. More precisely, if
402:
400:{\displaystyle K^{2}}
372:
278:surface and an orient
187:
109:, and more generally
76:
60:
48:
4131:Covariant derivative
3682:Topological manifold
3519:Invariance of domain
3471:Euler characteristic
3445:Bundle (mathematics)
3214:Orientation covering
2884:
2804:
2705:
2570:
2446:, the set of pairs (
2237:is orientable, then
2095:
1980:
1912:
1888:More precisely, let
1781:
1692:
1633:
1585:
1525:
1436:
1324:
1246:
1161:
1054:
988:
896:
661:, an orientation of
617:Jacobian determinant
463:) denotes the first
384:
341:
4165:Exterior derivative
3767:Atiyah–Singer index
3716:Riemannian manifold
3529:Tychonoff's theorem
3524:Poincaré conjecture
3278:General (point-set)
2652:space orientability
2648:Lorentzian geometry
2642:Lorentzian geometry
2506:is not orientable.
2088:is defined so that
1517:if and only if the
1151:long exact sequence
494:is orientable then
180:Orientable surfaces
4471:Secondary calculus
4425:Singularity theory
4380:Parallel transport
4148:De Rham cohomology
3787:Generalized Stokes
3514:De Rham cohomology
3435:Polyhedral complex
3425:Simplicial complex
3040:Algebraic Topology
2943:
2860:
2769:
2664:general relativity
2656:time orientability
2595:
2432:
2178:
2074:
1954:
1819:
1770:is orientable and
1752:
1663:
1615:
1555:
1521:th homology group
1488:
1376:
1316:if, at each point
1299:
1222:
1106:
1040:
976:around the origin
951:
840:. Conversely, if
509:, and if not then
507:free abelian group
415:Any surface has a
397:
367:
191:
170:differential forms
99:real vector spaces
95:topological spaces
83:
81:is non-orientable.
71:
55:
4506:
4505:
4388:
4387:
4153:Differential form
3807:Whitney embedding
3741:Differential form
3629:
3628:
3418:fundamental group
3080:Lawson, H. Blaine
3021:978-0-8053-9021-6
2968:Orientation sheaf
2963:Curve orientation
2796:associated bundle
2472:singular homology
2466:; here we assume
2450:, o) where
2423:
2345:is isomorphic to
2112:
2104:
1964:is isomorphic to
1908:chosen such that
1896:. To topologize
1155:relative homology
1050:is isomorphic to
879:local orientation
873:be a topological
16:(Redirected from
4531:
4498:Stratified space
4456:Fréchet manifold
4170:Interior product
4063:
3760:
3656:
3649:
3642:
3633:
3619:
3618:
3592:
3591:
3582:
3572:
3562:
3561:
3550:
3549:
3344:
3257:
3250:
3243:
3234:
3196:
3195:
3185:
3175:
3155:
3146:
3140:
3139:
3112:
3106:
3105:
3076:
3070:
3064:
3058:
3057:
3032:
3026:
3025:
3000:
2994:
2993:
2983:
2952:
2950:
2949:
2944:
2918:
2917:
2916:
2915:
2869:
2867:
2866:
2861:
2838:
2837:
2836:
2835:
2778:
2776:
2775:
2770:
2717:
2716:
2686:) has a pair of
2660:causal structure
2637:Related concepts
2604:
2602:
2601:
2596:
2585:
2584:
2424:
2363:
2301:
2224:
2220:
2204:
2187:
2185:
2184:
2179:
2162:
2158:
2157:
2123:
2122:
2113:
2110:
2105:
2102:
2083:
2081:
2080:
2075:
2073:
2069:
2068:
2034:
2033:
2018:
1992:
1991:
1963:
1961:
1960:
1955:
1950:
1924:
1923:
1884:
1877:
1871:
1861:
1854:
1828:
1826:
1825:
1820:
1812:
1807:
1793:
1792:
1761:
1759:
1758:
1753:
1745:
1740:
1726:
1725:
1704:
1703:
1672:
1670:
1669:
1664:
1659:
1645:
1644:
1628:
1624:
1622:
1621:
1616:
1611:
1597:
1596:
1580:
1564:
1562:
1561:
1556:
1551:
1537:
1536:
1497:
1495:
1494:
1489:
1487:
1483:
1482:
1448:
1447:
1404:
1385:
1383:
1382:
1377:
1375:
1371:
1370:
1336:
1335:
1308:
1306:
1305:
1300:
1298:
1294:
1293:
1285:
1284:
1264:
1263:
1241:
1231:
1229:
1228:
1223:
1221:
1213:
1209:
1208:
1200:
1199:
1179:
1178:
1148:
1144:
1137:
1129:
1115:
1113:
1112:
1107:
1105:
1101:
1100:
1066:
1065:
1049:
1047:
1046:
1041:
1039:
1035:
1034:
1000:
999:
982:excision theorem
960:
958:
957:
952:
947:
943:
942:
908:
907:
835:
823:
795:
770:
756:
743:. For example,
738:
709:
697:
671:
660:
645:
586:
488:torsion subgroup
486:) has a trivial
427:
406:
404:
403:
398:
396:
395:
376:
374:
373:
368:
366:
365:
353:
352:
225:
219:
151:
142:
103:Euclidean spaces
21:
4539:
4538:
4534:
4533:
4532:
4530:
4529:
4528:
4509:
4508:
4507:
4502:
4441:Banach manifold
4434:Generalizations
4429:
4384:
4321:
4218:
4180:Ricci curvature
4136:Cotangent space
4114:
4052:
3894:
3888:
3847:Exponential map
3811:
3756:
3750:
3670:
3660:
3630:
3625:
3556:
3538:
3534:Urysohn's lemma
3495:
3459:
3345:
3336:
3308:low-dimensional
3266:
3261:
3204:
3199:
3183:10.1.1.340.8125
3173:gr-qc/0202031v4
3166:(17): 4565–71.
3153:
3148:
3147:
3143:
3136:
3114:
3113:
3109:
3102:
3078:
3077:
3073:
3065:
3061:
3054:
3034:
3033:
3029:
3022:
3004:Spivak, Michael
3002:
3001:
2997:
2985:
2984:
2980:
2976:
2959:
2907:
2902:
2882:
2881:
2827:
2822:
2802:
2801:
2789:
2785:
2708:
2703:
2702:
2697:
2693:
2644:
2639:
2605:, the group of
2576:
2568:
2567:
2560:structure group
2552:structure group
2537:
2531:
2525:
2414:
2412:
2402:
2389:
2376:
2354:
2346:
2314:is a chart of ∂
2300:
2290:
2289:is fixed. Let
2271:
2222:
2218:
2195:
2128:
2124:
2114:
2093:
2092:
2039:
2035:
2025:
1983:
1978:
1977:
1915:
1910:
1909:
1879:
1873:
1863:
1856:
1850:
1843:
1784:
1779:
1778:
1777:vanishes, then
1776:
1717:
1695:
1690:
1689:
1679:
1636:
1631:
1630:
1626:
1588:
1583:
1582:
1578:
1528:
1523:
1522:
1453:
1449:
1439:
1434:
1433:
1399:
1341:
1337:
1327:
1322:
1321:
1270:
1269:
1265:
1249:
1244:
1243:
1237:
1185:
1184:
1180:
1164:
1159:
1158:
1146:
1139:
1131:
1121:
1071:
1067:
1057:
1052:
1051:
1005:
1001:
991:
986:
985:
913:
909:
899:
894:
893:
885:around a point
850:
825:
821:
812:
805:
794:
785:
779:
762:
748:
730:
699:
687:
685:structure group
666:
655:
640:
601:
581:
558:
515:
500:
481:
458:
450:
413:
387:
382:
381:
357:
344:
339:
338:
289:
199:Euclidean space
182:
162:homology theory
135:geometric shape
43:
28:
23:
22:
15:
12:
11:
5:
4537:
4535:
4527:
4526:
4521:
4511:
4510:
4504:
4503:
4501:
4500:
4495:
4490:
4485:
4480:
4479:
4478:
4468:
4463:
4458:
4453:
4448:
4443:
4437:
4435:
4431:
4430:
4428:
4427:
4422:
4417:
4412:
4407:
4402:
4396:
4394:
4390:
4389:
4386:
4385:
4383:
4382:
4377:
4372:
4367:
4362:
4357:
4352:
4347:
4342:
4337:
4331:
4329:
4323:
4322:
4320:
4319:
4314:
4309:
4304:
4299:
4294:
4289:
4279:
4274:
4269:
4259:
4254:
4249:
4244:
4239:
4234:
4228:
4226:
4220:
4219:
4217:
4216:
4211:
4206:
4205:
4204:
4194:
4189:
4188:
4187:
4177:
4172:
4167:
4162:
4161:
4160:
4150:
4145:
4144:
4143:
4133:
4128:
4122:
4120:
4116:
4115:
4113:
4112:
4107:
4102:
4097:
4096:
4095:
4085:
4080:
4075:
4069:
4067:
4060:
4054:
4053:
4051:
4050:
4045:
4035:
4030:
4016:
4011:
4006:
4001:
3996:
3994:Parallelizable
3991:
3986:
3981:
3980:
3979:
3969:
3964:
3959:
3954:
3949:
3944:
3939:
3934:
3929:
3924:
3914:
3904:
3898:
3896:
3890:
3889:
3887:
3886:
3881:
3876:
3874:Lie derivative
3871:
3869:Integral curve
3866:
3861:
3856:
3855:
3854:
3844:
3839:
3838:
3837:
3830:Diffeomorphism
3827:
3821:
3819:
3813:
3812:
3810:
3809:
3804:
3799:
3794:
3789:
3784:
3779:
3774:
3769:
3763:
3761:
3752:
3751:
3749:
3748:
3743:
3738:
3733:
3728:
3723:
3718:
3713:
3708:
3707:
3706:
3701:
3691:
3690:
3689:
3678:
3676:
3675:Basic concepts
3672:
3671:
3661:
3659:
3658:
3651:
3644:
3636:
3627:
3626:
3624:
3623:
3613:
3612:
3611:
3606:
3601:
3586:
3576:
3566:
3554:
3543:
3540:
3539:
3537:
3536:
3531:
3526:
3521:
3516:
3511:
3505:
3503:
3497:
3496:
3494:
3493:
3488:
3483:
3481:Winding number
3478:
3473:
3467:
3465:
3461:
3460:
3458:
3457:
3452:
3447:
3442:
3437:
3432:
3427:
3422:
3421:
3420:
3415:
3413:homotopy group
3405:
3404:
3403:
3398:
3393:
3388:
3383:
3373:
3368:
3363:
3353:
3351:
3347:
3346:
3339:
3337:
3335:
3334:
3329:
3324:
3323:
3322:
3312:
3311:
3310:
3300:
3295:
3290:
3285:
3280:
3274:
3272:
3268:
3267:
3262:
3260:
3259:
3252:
3245:
3237:
3231:
3230:
3223:
3217:
3211:
3203:
3202:External links
3200:
3198:
3197:
3141:
3134:
3107:
3100:
3071:
3059:
3053:978-0521795401
3052:
3036:Hatcher, Allen
3027:
3020:
2995:
2977:
2975:
2972:
2971:
2970:
2965:
2958:
2955:
2954:
2953:
2942:
2939:
2936:
2933:
2930:
2927:
2924:
2921:
2914:
2910:
2905:
2901:
2898:
2895:
2892:
2889:
2871:
2870:
2859:
2856:
2853:
2850:
2847:
2844:
2841:
2834:
2830:
2825:
2821:
2818:
2815:
2812:
2809:
2787:
2783:
2780:
2779:
2768:
2765:
2762:
2759:
2756:
2753:
2750:
2747:
2744:
2741:
2738:
2735:
2732:
2729:
2726:
2723:
2720:
2715:
2711:
2695:
2691:
2674:Formally, the
2643:
2640:
2638:
2635:
2627:tangent bundle
2615:tangent bundle
2609:with positive
2594:
2591:
2588:
2583:
2579:
2575:
2527:Main article:
2524:
2521:
2482:. This gives
2454:is a point of
2436:covering space
2411:
2408:
2398:
2385:
2372:
2350:
2298:
2270:
2267:
2261:is called the
2196:π :
2189:
2188:
2177:
2174:
2171:
2168:
2165:
2161:
2156:
2152:
2149:
2146:
2143:
2140:
2137:
2134:
2131:
2127:
2121:
2117:
2111: in
2108:
2103:Image of
2100:
2072:
2067:
2063:
2060:
2057:
2054:
2051:
2048:
2045:
2042:
2038:
2032:
2028:
2024:
2021:
2017:
2013:
2010:
2007:
2004:
2001:
1998:
1995:
1990:
1986:
1953:
1949:
1945:
1942:
1939:
1936:
1933:
1930:
1927:
1922:
1918:
1842:
1839:
1818:
1815:
1811:
1806:
1802:
1799:
1796:
1791:
1787:
1774:
1751:
1748:
1744:
1739:
1735:
1732:
1729:
1724:
1720:
1716:
1713:
1710:
1707:
1702:
1698:
1678:
1675:
1662:
1658:
1654:
1651:
1648:
1643:
1639:
1614:
1610:
1606:
1603:
1600:
1595:
1591:
1554:
1550:
1546:
1543:
1540:
1535:
1531:
1486:
1481:
1477:
1474:
1471:
1468:
1465:
1462:
1459:
1456:
1452:
1446:
1442:
1388:oriented atlas
1374:
1369:
1365:
1362:
1359:
1356:
1353:
1350:
1347:
1344:
1340:
1334:
1330:
1297:
1292:
1288:
1283:
1280:
1277:
1273:
1268:
1262:
1259:
1256:
1252:
1220:
1216:
1212:
1207:
1203:
1198:
1195:
1192:
1188:
1183:
1177:
1174:
1171:
1167:
1104:
1099:
1095:
1092:
1089:
1086:
1083:
1080:
1077:
1074:
1070:
1064:
1060:
1038:
1033:
1029:
1026:
1023:
1020:
1017:
1014:
1011:
1008:
1004:
998:
994:
962:
961:
950:
946:
941:
937:
934:
931:
928:
925:
922:
919:
916:
912:
906:
902:
877:-manifold. A
849:
846:
817:
810:
790:
783:
665:is a function
625:oriented atlas
600:
597:
557:
554:
513:
498:
479:
456:
449:
446:
422:If the figure
412:
409:
394:
390:
378:
377:
364:
360:
356:
351:
347:
288:
285:
261:surface normal
229:non-orientable
181:
178:
164:, whereas for
127:non-orientable
26:
24:
14:
13:
10:
9:
6:
4:
3:
2:
4536:
4525:
4522:
4520:
4517:
4516:
4514:
4499:
4496:
4494:
4493:Supermanifold
4491:
4489:
4486:
4484:
4481:
4477:
4474:
4473:
4472:
4469:
4467:
4464:
4462:
4459:
4457:
4454:
4452:
4449:
4447:
4444:
4442:
4439:
4438:
4436:
4432:
4426:
4423:
4421:
4418:
4416:
4413:
4411:
4408:
4406:
4403:
4401:
4398:
4397:
4395:
4391:
4381:
4378:
4376:
4373:
4371:
4368:
4366:
4363:
4361:
4358:
4356:
4353:
4351:
4348:
4346:
4343:
4341:
4338:
4336:
4333:
4332:
4330:
4328:
4324:
4318:
4315:
4313:
4310:
4308:
4305:
4303:
4300:
4298:
4295:
4293:
4290:
4288:
4284:
4280:
4278:
4275:
4273:
4270:
4268:
4264:
4260:
4258:
4255:
4253:
4250:
4248:
4245:
4243:
4240:
4238:
4235:
4233:
4230:
4229:
4227:
4225:
4221:
4215:
4214:Wedge product
4212:
4210:
4207:
4203:
4200:
4199:
4198:
4195:
4193:
4190:
4186:
4183:
4182:
4181:
4178:
4176:
4173:
4171:
4168:
4166:
4163:
4159:
4158:Vector-valued
4156:
4155:
4154:
4151:
4149:
4146:
4142:
4139:
4138:
4137:
4134:
4132:
4129:
4127:
4124:
4123:
4121:
4117:
4111:
4108:
4106:
4103:
4101:
4098:
4094:
4091:
4090:
4089:
4088:Tangent space
4086:
4084:
4081:
4079:
4076:
4074:
4071:
4070:
4068:
4064:
4061:
4059:
4055:
4049:
4046:
4044:
4040:
4036:
4034:
4031:
4029:
4025:
4021:
4017:
4015:
4012:
4010:
4007:
4005:
4002:
4000:
3997:
3995:
3992:
3990:
3987:
3985:
3982:
3978:
3975:
3974:
3973:
3970:
3968:
3965:
3963:
3960:
3958:
3955:
3953:
3950:
3948:
3945:
3943:
3940:
3938:
3935:
3933:
3930:
3928:
3925:
3923:
3919:
3915:
3913:
3909:
3905:
3903:
3900:
3899:
3897:
3891:
3885:
3882:
3880:
3877:
3875:
3872:
3870:
3867:
3865:
3862:
3860:
3857:
3853:
3852:in Lie theory
3850:
3849:
3848:
3845:
3843:
3840:
3836:
3833:
3832:
3831:
3828:
3826:
3823:
3822:
3820:
3818:
3814:
3808:
3805:
3803:
3800:
3798:
3795:
3793:
3790:
3788:
3785:
3783:
3780:
3778:
3775:
3773:
3770:
3768:
3765:
3764:
3762:
3759:
3755:Main results
3753:
3747:
3744:
3742:
3739:
3737:
3736:Tangent space
3734:
3732:
3729:
3727:
3724:
3722:
3719:
3717:
3714:
3712:
3709:
3705:
3702:
3700:
3697:
3696:
3695:
3692:
3688:
3685:
3684:
3683:
3680:
3679:
3677:
3673:
3668:
3664:
3657:
3652:
3650:
3645:
3643:
3638:
3637:
3634:
3622:
3614:
3610:
3607:
3605:
3602:
3600:
3597:
3596:
3595:
3587:
3585:
3581:
3577:
3575:
3571:
3567:
3565:
3560:
3555:
3553:
3545:
3544:
3541:
3535:
3532:
3530:
3527:
3525:
3522:
3520:
3517:
3515:
3512:
3510:
3507:
3506:
3504:
3502:
3498:
3492:
3491:Orientability
3489:
3487:
3484:
3482:
3479:
3477:
3474:
3472:
3469:
3468:
3466:
3462:
3456:
3453:
3451:
3448:
3446:
3443:
3441:
3438:
3436:
3433:
3431:
3428:
3426:
3423:
3419:
3416:
3414:
3411:
3410:
3409:
3406:
3402:
3399:
3397:
3394:
3392:
3389:
3387:
3384:
3382:
3379:
3378:
3377:
3374:
3372:
3369:
3367:
3364:
3362:
3358:
3355:
3354:
3352:
3348:
3343:
3333:
3330:
3328:
3327:Set-theoretic
3325:
3321:
3318:
3317:
3316:
3313:
3309:
3306:
3305:
3304:
3301:
3299:
3296:
3294:
3291:
3289:
3288:Combinatorial
3286:
3284:
3281:
3279:
3276:
3275:
3273:
3269:
3265:
3258:
3253:
3251:
3246:
3244:
3239:
3238:
3235:
3228:
3224:
3221:
3218:
3215:
3212:
3209:
3206:
3205:
3201:
3193:
3189:
3184:
3179:
3174:
3169:
3165:
3161:
3160:
3152:
3145:
3142:
3137:
3135:0-521-20016-4
3131:
3127:
3126:
3121:
3120:Ellis, G.F.R.
3117:
3116:Hawking, S.W.
3111:
3108:
3103:
3101:0-691-08542-0
3097:
3093:
3089:
3088:Spin Geometry
3085:
3081:
3075:
3072:
3068:
3063:
3060:
3055:
3049:
3045:
3041:
3037:
3031:
3028:
3023:
3017:
3013:
3012:HarperCollins
3009:
3005:
2999:
2996:
2991:
2990:
2982:
2979:
2973:
2969:
2966:
2964:
2961:
2960:
2956:
2940:
2934:
2931:
2928:
2925:
2922:
2912:
2908:
2903:
2896:
2890:
2880:
2879:
2878:
2876:
2854:
2851:
2848:
2845:
2842:
2832:
2828:
2823:
2816:
2810:
2800:
2799:
2798:
2797:
2793:
2766:
2760:
2757:
2754:
2751:
2748:
2736:
2733:
2730:
2724:
2718:
2713:
2709:
2701:
2700:
2699:
2689:
2685:
2681:
2677:
2672:
2669:
2665:
2661:
2657:
2653:
2649:
2641:
2636:
2634:
2632:
2628:
2624:
2620:
2616:
2612:
2608:
2589:
2581:
2577:
2573:
2565:
2561:
2557:
2553:
2550:
2546:
2542:
2541:vector bundle
2536:
2530:
2522:
2520:
2518:
2513:
2507:
2505:
2501:
2497:
2493:
2490:, o) to
2489:
2485:
2481:
2477:
2473:
2469:
2465:
2461:
2457:
2453:
2449:
2445:
2441:
2437:
2429:
2409:
2407:
2405:
2401:
2397:
2393:
2388:
2384:
2380:
2375:
2371:
2367:
2362:
2358:
2353:
2349:
2344:
2340:
2336:
2332:
2328:
2323:
2321:
2317:
2313:
2309:
2305:
2297:
2293:
2288:
2284:
2280:
2276:
2268:
2266:
2264:
2260:
2256:
2252:
2248:
2244:
2240:
2236:
2232:
2228:
2216:
2212:
2208:
2203:
2199:
2192:
2172:
2169:
2166:
2163:
2159:
2150:
2144:
2135:
2132:
2129:
2125:
2119:
2115:
2106:
2091:
2090:
2089:
2087:
2070:
2061:
2055:
2046:
2043:
2040:
2036:
2030:
2026:
2011:
2008:
2002:
1999:
1996:
1988:
1984:
1975:
1971:
1967:
1943:
1940:
1934:
1931:
1928:
1920:
1916:
1907:
1903:
1899:
1895:
1891:
1886:
1882:
1876:
1870:
1866:
1859:
1853:
1848:
1840:
1838:
1836:
1832:
1813:
1809:
1800:
1797:
1789:
1785:
1773:
1769:
1765:
1746:
1742:
1733:
1730:
1722:
1718:
1714:
1708:
1700:
1696:
1688:
1684:
1676:
1674:
1652:
1649:
1641:
1637:
1604:
1601:
1593:
1589:
1576:
1572:
1568:
1544:
1541:
1533:
1529:
1520:
1516:
1512:
1508:
1503:
1501:
1484:
1475:
1469:
1460:
1457:
1454:
1450:
1444:
1440:
1431:
1427:
1423:
1419:
1414:
1412:
1408:
1402:
1397:
1393:
1389:
1372:
1363:
1357:
1348:
1345:
1342:
1338:
1332:
1328:
1319:
1315:
1310:
1295:
1286:
1281:
1278:
1275:
1271:
1266:
1260:
1257:
1254:
1250:
1240:
1235:
1214:
1210:
1201:
1196:
1193:
1190:
1186:
1181:
1175:
1172:
1169:
1165:
1156:
1152:
1142:
1135:
1128:
1124:
1119:
1102:
1093:
1087:
1078:
1075:
1072:
1068:
1062:
1058:
1036:
1027:
1021:
1012:
1009:
1006:
1002:
996:
992:
983:
979:
975:
971:
967:
948:
944:
935:
929:
920:
917:
914:
910:
904:
900:
892:
891:
890:
888:
884:
880:
876:
872:
868:
864:
859:
854:
847:
845:
843:
839:
833:
829:
820:
816:
809:
803:
799:
793:
789:
782:
776:
774:
769:
765:
760:
755:
751:
746:
742:
737:
734:
728:
724:
719:
717:
713:
707:
703:
695:
691:
686:
682:
679:, so it is a
678:
677:vector bundle
673:
669:
664:
658:
653:
649:
643:
638:
634:
630:
626:
622:
618:
614:
610:
606:
598:
596:
594:
590:
584:
579:
575:
571:
567:
563:
555:
553:
551:
547:
543:
539:
535:
531:
527:
523:
519:
512:
508:
504:
497:
493:
489:
485:
478:
474:
470:
466:
462:
455:
447:
445:
443:
440:> 4 some
439:
435:
430:
426:
420:
418:
417:triangulation
410:
408:
392:
388:
362:
358:
354:
349:
345:
337:
336:
335:
333:
328:
324:
322:
318:
314:
313:Klein bottles
310:
306:
305:Möbius strips
302:
298:
294:
286:
284:
281:
277:
273:
269:
265:
262:
258:
257:
252:
251:
245:
243:
239:
235:
231:
230:
224:
218:
213:
209:
208:
203:
200:
196:
186:
179:
177:
175:
171:
167:
163:
157:
155:
150:
146:
141:
136:
132:
128:
124:
120:
116:
112:
108:
104:
100:
96:
92:
91:orientability
88:
80:
79:Roman surface
75:
68:
64:
59:
52:
47:
41:
37:
33:
19:
4420:Moving frame
4415:Morse theory
4405:Gauge theory
4197:Tensor field
4126:Closed/Exact
4105:Vector field
4073:Distribution
4014:Hypercomplex
4009:Quaternionic
3988:
3746:Vector field
3704:Smooth atlas
3621:Publications
3490:
3486:Chern number
3476:Betti number
3359: /
3350:Key concepts
3298:Differential
3163:
3157:
3144:
3124:
3110:
3087:
3074:
3067:Hatcher 2001
3062:
3039:
3030:
3007:
2998:
2988:
2981:
2874:
2872:
2781:
2683:
2679:
2673:
2645:
2630:
2555:
2554:, is called
2544:
2538:
2516:
2508:
2503:
2499:
2495:
2491:
2487:
2483:
2479:
2475:
2467:
2463:
2459:
2455:
2451:
2447:
2443:
2439:
2433:
2428:Möbius strip
2403:
2399:
2395:
2391:
2386:
2382:
2378:
2373:
2369:
2365:
2360:
2356:
2351:
2347:
2342:
2338:
2334:
2330:
2326:
2324:
2319:
2315:
2311:
2307:
2303:
2295:
2291:
2286:
2282:
2278:
2274:
2272:
2262:
2258:
2254:
2250:
2246:
2242:
2238:
2234:
2230:
2226:
2221:. In fact,
2214:
2210:
2206:
2201:
2197:
2193:
2190:
2085:
1973:
1969:
1965:
1905:
1901:
1897:
1893:
1889:
1887:
1880:
1874:
1868:
1864:
1857:
1851:
1846:
1844:
1834:
1771:
1767:
1763:
1682:
1680:
1574:
1570:
1566:
1518:
1514:
1510:
1506:
1504:
1499:
1429:
1425:
1421:
1417:
1415:
1410:
1406:
1400:
1395:
1391:
1387:
1317:
1313:
1311:
1238:
1233:
1140:
1133:
1126:
1122:
1117:
1116:. The ball
977:
973:
969:
965:
963:
886:
882:
878:
874:
870:
866:
862:
857:
855:
851:
841:
837:
831:
827:
818:
814:
807:
802:right-handed
801:
797:
791:
787:
780:
777:
772:
767:
763:
758:
753:
749:
744:
740:
735:
732:
726:
723:volume forms
720:
715:
711:
705:
701:
693:
689:
681:fiber bundle
674:
667:
662:
656:
651:
647:
641:
636:
632:
628:
624:
620:
612:
608:
604:
602:
592:
588:
582:
577:
573:
565:
561:
559:
549:
548:embedded in
541:
537:
533:
529:
525:
521:
517:
510:
502:
495:
491:
483:
476:
472:
468:
460:
453:
451:
441:
437:
433:
431:
421:
414:
379:
331:
329:
325:
316:
290:
279:
275:
271:
267:
263:
255:
254:
249:
248:
246:
242:Möbius strip
238:homeomorphic
228:
227:
206:
205:
201:
194:
192:
174:fiber bundle
158:
154:Möbius strip
145:mirror image
126:
118:
114:
90:
84:
63:Möbius strip
4365:Levi-Civita
4355:Generalized
4327:Connections
4277:Lie algebra
4209:Volume form
4110:Vector flow
4083:Pushforward
4078:Lie bracket
3977:Lie algebra
3942:G-structure
3731:Pushforward
3711:Submanifold
3584:Wikiversity
3501:Key results
3227:Orientation
2613:. For the
2611:determinant
2535:Euler class
1681:A manifold
1571:orientation
1407:orientation
865:but not at
648:orientation
546:Möbius band
250:orientation
119:orientation
87:mathematics
4513:Categories
4488:Stratifold
4446:Diffeology
4242:Associated
4043:Symplectic
4028:Riemannian
3957:Hyperbolic
3884:Submersion
3792:Hopf–Rinow
3726:Submersion
3721:Smooth map
3430:CW complex
3371:Continuity
3361:Closed set
3320:cohomology
2974:References
2688:characters
2556:orientable
2533:See also:
1515:orientable
1396:orientable
980:. By the
637:orientable
270:or −
207:orientable
193:A surface
137:, such as
115:orientable
18:Orientable
4370:Principal
4345:Ehresmann
4302:Subbundle
4292:Principal
4267:Fibration
4247:Cotangent
4119:Covectors
3972:Lie group
3952:Hermitian
3895:manifolds
3864:Immersion
3859:Foliation
3797:Noether's
3782:Frobenius
3777:De Rham's
3772:Darboux's
3663:Manifolds
3609:geometric
3604:algebraic
3455:Cobordism
3391:Hausdorff
3386:connected
3303:Geometric
3293:Continuum
3283:Algebraic
3178:CiteSeerX
2923:−
2913:−
2909:σ
2904:×
2891:
2843:−
2829:σ
2824:×
2811:
2749:−
2743:→
2725:
2714:±
2710:σ
2668:spacetime
2558:when the
2191:is open.
2170:∈
2164::
2139:∖
2107:α
2050:∖
2023:→
2006:∖
1938:∖
1715:∈
1464:∖
1352:∖
1279:−
1258:−
1215:≅
1194:−
1173:−
1082:∖
1016:∖
924:∖
355:×
111:manifolds
4524:Surfaces
4466:Orbifold
4461:K-theory
4451:Diffiety
4175:Pullback
3989:Oriented
3967:Kenmotsu
3947:Hadamard
3893:Types of
3842:Geodesic
3667:Glossary
3574:Wikibook
3552:Category
3440:Manifold
3408:Homotopy
3366:Interior
3357:Open set
3315:Homology
3264:Topology
3122:(1973).
3086:(1989).
3038:(2001).
3006:(1965).
2957:See also
2873:where O(
2623:manifold
2607:matrices
2545:a priori
2543:, which
822:) > 0
570:manifold
465:homology
321:immersed
287:Examples
256:oriented
234:manifold
107:surfaces
97:such as
4410:History
4393:Related
4307:Tangent
4285:)
4265:)
4232:Adjoint
4224:Bundles
4202:density
4100:Torsion
4066:Vectors
4058:Tensors
4041:)
4026:)
4022:,
4020:Pseudo−
3999:Poisson
3932:Finsler
3927:Fibered
3922:Contact
3920:)
3912:Complex
3910:)
3879:Section
3599:general
3401:uniform
3381:compact
3332:Digital
2794:of the
2792:section
2788:−
2696:−
2564:reduced
2562:may be
2539:A real
1883:′
1860:′
806:ω(
591:, then
505:) is a
471:, then
319:, only
293:Spheres
240:to the
197:in the
123:spheres
4375:Vector
4360:Koszul
4340:Cartan
4335:Affine
4317:Vector
4312:Tensor
4297:Spinor
4287:Normal
4283:Stable
4237:Affine
4141:bundle
4093:bundle
4039:Almost
3962:Kähler
3918:Almost
3908:Almost
3902:Closed
3802:Sard's
3758:(list)
3594:Topics
3396:metric
3271:Fields
3180:
3132:
3098:
3050:
3018:
2786:σ
2631:always
2619:smooth
2547:has a
2249:. If
2233:. If
2223:π
2219:π
1627:α
1579:α
1569:. An
1403:> 0
1130:is an
773:ω
752:∧ ⋯ ∧
727:ω
670:→ {±1}
644:> 0
623:. An
532:where
311:, and
299:, and
297:planes
212:chiral
4483:Sheaf
4257:Fiber
4033:Rizza
4004:Prime
3835:Local
3825:Curve
3687:Atlas
3376:Space
3168:arXiv
3154:(PDF)
2621:real
2549:GL(n)
2512:index
2442:take
2325:When
1833:over
1405:, an
813:, …,
786:, …,
683:with
646:, an
210:if a
131:loops
51:torus
4350:Form
4252:Dual
4185:flow
4048:Tame
4024:Sub−
3937:Flat
3817:Maps
3130:ISBN
3096:ISBN
3048:ISBN
3016:ISBN
2666:, a
2654:and
2458:and
2341:to ∂
2333:of ∂
1878:and
1145:and
1136:− 1)
611:are
560:Let
520:) =
301:tori
280:able
152:. A
77:The
67:disk
61:The
4272:Jet
3188:doi
2646:In
2566:to
2273:If
2209:to
1972:in
1573:of
1513:is
1409:of
1394:is
1153:in
1143:− 1
881:of
826:GL(
804:if
729:of
700:GL(
688:GL(
672:.)
659:= 0
650:of
635:is
627:on
585:= 0
452:If
204:is
85:In
4515::
4263:Co
3186:.
3176:.
3164:19
3162:.
3156:.
3118:;
3090:.
3082:;
3046:.
3042:.
3014:.
3010:.
2698:,
2678:O(
2406:.
2359:⊕
2322:.
2294:→
2265:.
2200:→
1867:→
1673:.
1125:\
984:,
830:,
766:→
754:dx
750:dx
731:⋀
704:,
692:,
552:.
540:/2
528:/2
524:+
307:,
295:,
276:ed
105:,
101:,
89:,
49:A
4281:(
4261:(
4037:(
4018:(
3916:(
3906:(
3669:)
3665:(
3655:e
3648:t
3641:v
3256:e
3249:t
3242:v
3229:.
3194:.
3190::
3170::
3138:.
3104:.
3056:.
3024:.
2941:.
2938:}
2935:1
2932:+
2929:,
2926:1
2920:{
2900:)
2897:M
2894:(
2888:O
2875:M
2858:}
2855:1
2852:+
2849:,
2846:1
2840:{
2833:+
2820:)
2817:M
2814:(
2808:O
2784:+
2767:.
2764:}
2761:1
2758:+
2755:,
2752:1
2746:{
2740:)
2737:q
2734:,
2731:p
2728:(
2722:O
2719::
2692:+
2684:q
2682:,
2680:p
2593:)
2590:n
2587:(
2582:+
2578:L
2574:G
2517:M
2504:M
2500:M
2492:x
2488:x
2484:M
2480:M
2476:M
2468:M
2464:x
2460:o
2456:M
2452:x
2448:x
2444:M
2440:M
2430:.
2404:M
2400:p
2396:T
2392:M
2390:∂
2387:p
2383:T
2379:M
2377:∂
2374:p
2370:T
2366:R
2361:R
2357:M
2355:∂
2352:p
2348:T
2343:M
2339:M
2335:M
2331:p
2327:M
2320:M
2316:M
2312:M
2308:M
2304:M
2299:+
2296:R
2292:U
2287:M
2283:M
2279:M
2275:M
2259:O
2255:O
2251:M
2247:M
2243:O
2239:M
2235:M
2231:U
2227:U
2215:M
2211:p
2207:p
2202:M
2198:O
2176:}
2173:U
2167:p
2160:)
2155:Z
2151:;
2148:}
2145:p
2142:{
2136:M
2133:,
2130:M
2126:(
2120:n
2116:H
2099:{
2086:O
2071:)
2066:Z
2062:;
2059:}
2056:p
2053:{
2047:M
2044:,
2041:M
2037:(
2031:n
2027:H
2020:)
2016:Z
2012:;
2009:U
2003:M
2000:,
1997:M
1994:(
1989:n
1985:H
1974:U
1970:p
1966:Z
1952:)
1948:Z
1944:;
1941:U
1935:M
1932:,
1929:M
1926:(
1921:n
1917:H
1906:M
1902:U
1898:O
1894:M
1890:O
1881:p
1875:p
1869:R
1865:U
1858:p
1852:p
1847:M
1835:M
1817:)
1814:2
1810:/
1805:Z
1801:;
1798:M
1795:(
1790:0
1786:H
1775:1
1772:w
1768:M
1764:Z
1750:)
1747:2
1743:/
1738:Z
1734:;
1731:M
1728:(
1723:1
1719:H
1712:)
1709:M
1706:(
1701:1
1697:w
1683:M
1661:)
1657:Z
1653:;
1650:M
1647:(
1642:n
1638:H
1613:)
1609:Z
1605:;
1602:M
1599:(
1594:n
1590:H
1575:M
1567:Z
1553:)
1549:Z
1545:;
1542:M
1539:(
1534:n
1530:H
1519:n
1511:M
1507:M
1500:p
1485:)
1480:Z
1476:;
1473:}
1470:p
1467:{
1461:M
1458:,
1455:M
1451:(
1445:n
1441:H
1430:p
1426:p
1422:M
1418:M
1411:M
1401:n
1392:M
1373:)
1368:Z
1364:;
1361:}
1358:p
1355:{
1349:M
1346:,
1343:M
1339:(
1333:n
1329:H
1318:p
1296:)
1291:Z
1287:;
1282:1
1276:n
1272:S
1267:(
1261:1
1255:n
1251:H
1239:R
1234:p
1219:Z
1211:)
1206:Z
1202:;
1197:1
1191:n
1187:S
1182:(
1176:1
1170:n
1166:H
1147:0
1141:n
1134:n
1132:(
1127:O
1123:B
1118:B
1103:)
1098:Z
1094:;
1091:}
1088:O
1085:{
1079:B
1076:,
1073:B
1069:(
1063:n
1059:H
1037:)
1032:Z
1028:;
1025:}
1022:p
1019:{
1013:M
1010:,
1007:M
1003:(
997:n
993:H
978:O
974:B
970:p
966:p
949:.
945:)
940:Z
936:;
933:}
930:p
927:{
921:M
918:,
915:M
911:(
905:n
901:H
887:p
883:M
875:n
871:M
867:p
863:p
858:p
842:M
838:M
834:)
832:R
828:n
819:n
815:X
811:1
808:X
798:p
792:n
788:X
784:1
781:X
768:R
764:U
759:M
745:R
741:M
736:M
733:T
716:M
712:M
708:)
706:R
702:n
696:)
694:R
690:n
668:M
663:M
657:n
652:M
642:n
633:M
629:M
613:C
609:M
605:M
593:M
589:M
583:n
578:M
574:M
568:-
566:n
562:M
550:S
542:Z
538:Z
534:F
530:Z
526:Z
522:F
518:S
516:(
514:1
511:H
503:S
501:(
499:1
496:H
492:S
484:S
482:(
480:1
477:H
473:S
469:S
461:S
459:(
457:1
454:H
442:n
438:n
434:n
393:2
389:K
363:1
359:S
350:2
346:K
332:R
317:R
272:n
268:n
264:n
202:R
195:S
42:.
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.