28:
20:
94:. In that problem, the original sheet is a plain rectangle without holes. The challenge comes from the fact that the dimensions of the small rectangles are fixed in advance. The optimization goals are usually to maximize the area of the produced rectangles or their value, or minimize the waste or the number of required sheets.
221:
In the special case in which all holes are degenerate (single points), the minimum-length guillotine rectangular partition is at most 2 times the minimum-length rectangular partition. By a more careful analysis, it can be proved that the approximation factor is in fact at most 1.75. It is not known
343:
Besides the computational problems, guillotine partitions were also studied from a combinatorial perspective. Suppose a given rectangle should be partitioned into smaller rectangles using guillotine cuts only. Obviously, there are infinitely many ways to do this, since even a single cut can take
549:
634:
222:
if the 1.75 is tight, but there is an instance in which the approximation factor is 1.5. Therefore, the guillotine partition provides a constant-factor approximation to the general problem, which is NP-hard.
427:
275:
322:
216:
143:
180:
1260:
926:"Guillotine Subdivisions Approximate Polygonal Subdivisions: A Simple Polynomial-Time Approximation Scheme for Geometric TSP, k-MST, and Related Problems"
449:
23:
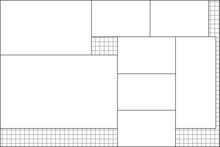
A guillotine cutting: an optimised sheet of smaller rectangles which can be divided intact through the correct series of bisecting end-to-end cuts.
558:
1195:
779:
744:
332:
1270:
900:
151:
there exists a minimum-length guillotine rectangular partition in which every maximal line segment contains a vertex of the boundary
842:
355:
81:
related to guillotine partition, such as: minimizing the number of rectangles or the total length of cuts. These are variants of
1217:
1055:
672:-coloring always exists. An important special case is when the graph represents a partition of a rectangle into rectangles.
106:, the goal is to partition the original rectilinear polygon into rectangles, such that the total edge length is a minimum.
62:
774:. Springer Optimization and Its Applications. New York: Springer-Verlag. pp. 165–209, chapter 5 "guillotine cut".
1265:
703:
74:
693:
Dimitrov, Aigner-Horev and
Krakovski finally proved that there always exists a strong polychromatic 4-coloring.
679:
Aigner-Horev, Katz, Krakovski and
Loffler proved that, in the special sub-case in which the graph represents a
54:) is a straight bisecting line going from one edge of an existing polygon to the opposite edge, similarly to a
653:
446:
dimensions, Ackerman, Barequet, Pinter and Romik give an exact summation formula, and prove that it is in
1132:
1011:
78:
1093:
664:
of the graph, each color appears at least once. Several researchers have tried to find the largest
661:
146:
43:
232:
1171:
992:
906:
90:
434:
1236:
1191:
1152:
1113:
1074:
1031:
984:
945:
896:
861:
818:
775:
740:
284:
185:
112:
82:
1226:
1183:
1144:
1105:
1064:
1023:
976:
937:
888:
851:
808:
732:
55:
925:
27:
836:
Gonzalez, Teofilo F.; Razzazi, Mohammadreza; Shing, Man-Tak; Zheng, Si-Qing (1994-05-01).
156:
229:-dimensional box: a guillotine-partition with minimum edge-length can be found in time
19:
881:"Polynomial time approximation schemes for Euclidean TSP and other geometric problems"
813:
796:
676:
Dinitz, Katz and
Krakovski proved that there always exists a polychromatic 3-coloring.
1254:
856:
837:
996:
910:
657:
544:{\displaystyle \Theta \left({\frac {(2d-1+2{\sqrt {d(d-1)}})^{n}}{n^{3/2}}}\right)}
430:
1187:
1049:
Asinowski, Andrei; Barequet, Gill; Mansour, Toufik; Pinter, Ron Y. (2014-09-28).
769:
724:
690:-dimensional guillotine partitions, and provided an efficient coloring algorithm.
46:, possibly containing some holes, into rectangles, using only guillotine-cuts. A
736:
1231:
1212:
1069:
1050:
1148:
1131:
Horev, Elad; Katz, Matthew J.; Krakovski, Roi; Löffler, Maarten (2009-06-15).
1109:
1027:
941:
880:
1240:
1156:
1117:
1078:
1035:
988:
949:
892:
865:
822:
629:{\displaystyle \Theta \left({\frac {(3+2{\sqrt {2}})^{n}}{n^{3/2}}}\right)}
980:
1010:
Ackerman, Eyal; Barequet, Gill; Pinter, Ron Y.; Romik, Dan (2006-05-31).
838:"On optimal guillotine partitions approximating optimal d-box partitions"
331:
Arora and
Mitchell used the guillotine-partitioning technique to develop
964:
963:
Yao, Bo; Chen, Hongyu; Cheng, Chung-Kuan; Graham, Ronald (2003-01-01).
182:
possible choices for the next guillotine cut, and there are altogether
65:. An alternative term for a guillotine-partition in this context is a
1098:
International
Journal of Computational Geometry & Applications
26:
18:
885:
Proceedings of 37th
Conference on Foundations of Computer Science
639:
Asinowski, Barequet, Mansour and Pinter also study the number of
1172:"Polychromatic Colorings of n-Dimensional Guillotine-Partitions"
85:
problems, where the cuts are constrained to be guillotine cuts.
1092:
Dinitz, Yefim; Katz, Matthew J.; Krakovski, Roi (2009-12-01).
35:
be separated by making single bisecting cuts across the plane.
73:. Guillotine partitions are also the underlying structure of
98:
Computing a guillotine partition with a smallest edge-length
1211:
Dimitrov, Darko; Horev, Elad; Krakovski, Roi (2009-05-06).
969:
ACM Transactions on Design
Automation of Electronic Systems
797:"Improved bounds for rectangular and guillotine partitions"
422:{\displaystyle O\left({\frac {n!2^{5n-3}}{n^{3/2}}}\right)}
281:-1)-volume in the optimal guillotine-partition is at most
61:
Guillotine partition is particularly common in designing
1170:
Keszegh, Balázs (2008). Hu, Xiaodong; Wang, Jie (eds.).
1051:"Cut equivalence of d-dimensional guillotine partitions"
965:"Floorplan representations: Complexity and connections"
731:, Wiesbaden: Vieweg+Teubner Verlag, pp. 251–301,
729:
Combinatorial
Algorithms for Integrated Circuit Layout
145:
even if the raw polygon has holes. The algorithm uses
1133:"Polychromatic 4-coloring of guillotine subdivisions"
1012:"The number of guillotine partitions in d dimensions"
561:
452:
358:
287:
235:
188:
159:
115:
1213:"Polychromatic colorings of rectangular partitions"
683:, a strong polychromatic 4-coloring always exists.
628:
543:
421:
316:
269:
210:
174:
137:
660:is a coloring of its vertices such that, in each
104:minimum edge-length rectangular-partition problem
795:Gonzalez, Teofilo; Zheng, Si-Qing (1989-06-01).
771:Design and Analysis of Approximation Algorithms
768:Du, Ding-Zhu; Ko, Ker-I.; Hu, Xiaodong (2012).
344:infinitely many values. However, the number of
352:In two dimensions, there is an upper bound in
335:for various geometric optimization problems.
16:Process of partitioning a rectilinear polygon
8:
31:A non-guillotine cutting: these rectangles
153:. Therefore, in each iteration, there are
1230:
1182:. Berlin, Heidelberg: Springer: 110–118.
1068:
855:
812:
610:
606:
595:
584:
569:
560:
525:
521:
510:
484:
460:
451:
403:
399:
379:
366:
357:
306:
286:
249:
234:
199:
187:
158:
126:
114:
715:
1178:. Lecture Notes in Computer Science.
924:Mitchell, Joseph S. B. (1999-01-01).
333:polynomial-time approximation schemes
7:
763:
761:
149:based on the following observation:
1261:Optimization algorithms and methods
225:These results can be extended to a
109:This problem can be solved in time
88:A related but different problem is
562:
453:
348:guillotine partitions is bounded.
14:
1094:"Guarding rectangular partitions"
42:is the process of partitioning a
686:Keszegh extended this result to
801:Journal of Symbolic Computation
339:Number of guillotine partitions
1137:Information Processing Letters
1016:Information Processing Letters
648:Coloring guillotine partitions
592:
572:
507:
501:
489:
463:
264:
239:
205:
192:
169:
163:
132:
119:
63:floorplans in microelectronics
1:
814:10.1016/S0747-7171(89)80042-2
1188:10.1007/978-3-540-69733-6_12
857:10.1016/0925-7721(94)90013-2
270:{\displaystyle O(dn^{2d+1})}
1176:Computing and Combinatorics
737:10.1007/978-3-322-92106-2_6
1287:
1232:10.1016/j.disc.2008.07.035
1070:10.1016/j.disc.2014.05.014
879:Arora, S. (October 1996).
668:such that a polychromatic
433:. the exact number is the
1149:10.1016/j.ipl.2009.03.006
1110:10.1142/S0218195909003131
1028:10.1016/j.ipl.2006.01.011
942:10.1137/S0097539796309764
930:SIAM Journal on Computing
723:Lengauer, Thomas (1990),
704:Binary space partitioning
643:of guillotine partitions.
324:times that of an optimal
1271:Rectangular subdivisions
893:10.1109/SFCS.1996.548458
317:{\displaystyle 2d-4+4/d}
211:{\displaystyle O(n^{4})}
138:{\displaystyle O(n^{5})}
641:cut-equivalence classes
75:binary space partitions
843:Computational Geometry
725:"Circuit Partitioning"
654:polychromatic coloring
630:
555:=2 this bound becomes
545:
423:
346:structurally-different
318:
271:
212:
176:
139:
36:
24:
981:10.1145/606603.606607
631:
546:
424:
319:
272:
213:
177:
140:
79:optimization problems
30:
22:
1218:Discrete Mathematics
1056:Discrete Mathematics
681:guillotine partition
559:
450:
356:
285:
233:
186:
175:{\displaystyle O(n)}
157:
113:
83:polygon partitioning
77:. There are various
40:Guillotine partition
147:dynamic programming
44:rectilinear polygon
626:
541:
419:
314:
267:
208:
172:
135:
91:guillotine cutting
37:
25:
1266:Discrete geometry
1197:978-3-540-69733-6
887:. pp. 2–11.
781:978-1-4614-1700-2
746:978-3-322-92108-6
620:
589:
535:
504:
413:
277:, and the total (
71:slicing floorplan
67:slicing partition
1278:
1245:
1244:
1234:
1225:(9): 2957–2960.
1208:
1202:
1201:
1167:
1161:
1160:
1128:
1122:
1121:
1089:
1083:
1082:
1072:
1046:
1040:
1039:
1007:
1001:
1000:
960:
954:
953:
936:(4): 1298–1309.
921:
915:
914:
876:
870:
869:
859:
833:
827:
826:
816:
792:
786:
785:
765:
756:
755:
754:
753:
720:
635:
633:
632:
627:
625:
621:
619:
618:
614:
601:
600:
599:
590:
585:
570:
550:
548:
547:
542:
540:
536:
534:
533:
529:
516:
515:
514:
505:
485:
461:
428:
426:
425:
420:
418:
414:
412:
411:
407:
394:
393:
392:
367:
328:-box partition.
323:
321:
320:
315:
310:
276:
274:
273:
268:
263:
262:
217:
215:
214:
209:
204:
203:
181:
179:
178:
173:
144:
142:
141:
136:
131:
130:
56:paper guillotine
52:edge-to-edge cut
50:(also called an
1286:
1285:
1281:
1280:
1279:
1277:
1276:
1275:
1251:
1250:
1249:
1248:
1210:
1209:
1205:
1198:
1169:
1168:
1164:
1143:(13): 690–694.
1130:
1129:
1125:
1091:
1090:
1086:
1048:
1047:
1043:
1009:
1008:
1004:
962:
961:
957:
923:
922:
918:
903:
878:
877:
873:
835:
834:
830:
794:
793:
789:
782:
767:
766:
759:
751:
749:
747:
722:
721:
717:
712:
700:
650:
602:
591:
571:
565:
557:
556:
517:
506:
462:
456:
448:
447:
435:Schröder number
395:
375:
368:
362:
354:
353:
341:
283:
282:
245:
231:
230:
195:
184:
183:
155:
154:
122:
111:
110:
100:
17:
12:
11:
5:
1284:
1282:
1274:
1273:
1268:
1263:
1253:
1252:
1247:
1246:
1203:
1196:
1162:
1123:
1104:(6): 579–594.
1084:
1041:
1022:(4): 162–167.
1002:
955:
916:
901:
871:
828:
807:(6): 591–610.
787:
780:
757:
745:
714:
713:
711:
708:
707:
706:
699:
696:
695:
694:
691:
684:
677:
649:
646:
645:
644:
637:
624:
617:
613:
609:
605:
598:
594:
588:
583:
580:
577:
574:
568:
564:
539:
532:
528:
524:
520:
513:
509:
503:
500:
497:
494:
491:
488:
483:
480:
477:
474:
471:
468:
465:
459:
455:
440:
438:
429:attributed to
417:
410:
406:
402:
398:
391:
388:
385:
382:
378:
374:
371:
365:
361:
340:
337:
313:
309:
305:
302:
299:
296:
293:
290:
266:
261:
258:
255:
252:
248:
244:
241:
238:
207:
202:
198:
194:
191:
171:
168:
165:
162:
134:
129:
125:
121:
118:
99:
96:
48:guillotine-cut
15:
13:
10:
9:
6:
4:
3:
2:
1283:
1272:
1269:
1267:
1264:
1262:
1259:
1258:
1256:
1242:
1238:
1233:
1228:
1224:
1220:
1219:
1214:
1207:
1204:
1199:
1193:
1189:
1185:
1181:
1177:
1173:
1166:
1163:
1158:
1154:
1150:
1146:
1142:
1138:
1134:
1127:
1124:
1119:
1115:
1111:
1107:
1103:
1099:
1095:
1088:
1085:
1080:
1076:
1071:
1066:
1062:
1058:
1057:
1052:
1045:
1042:
1037:
1033:
1029:
1025:
1021:
1017:
1013:
1006:
1003:
998:
994:
990:
986:
982:
978:
974:
970:
966:
959:
956:
951:
947:
943:
939:
935:
931:
927:
920:
917:
912:
908:
904:
902:0-8186-7594-2
898:
894:
890:
886:
882:
875:
872:
867:
863:
858:
853:
849:
845:
844:
839:
832:
829:
824:
820:
815:
810:
806:
802:
798:
791:
788:
783:
777:
773:
772:
764:
762:
758:
748:
742:
738:
734:
730:
726:
719:
716:
709:
705:
702:
701:
697:
692:
689:
685:
682:
678:
675:
674:
673:
671:
667:
663:
659:
655:
647:
642:
638:
622:
615:
611:
607:
603:
596:
586:
581:
578:
575:
566:
554:
537:
530:
526:
522:
518:
511:
498:
495:
492:
486:
481:
478:
475:
472:
469:
466:
457:
445:
441:
439:
436:
432:
415:
408:
404:
400:
396:
389:
386:
383:
380:
376:
372:
369:
363:
359:
351:
350:
349:
347:
338:
336:
334:
329:
327:
311:
307:
303:
300:
297:
294:
291:
288:
280:
259:
256:
253:
250:
246:
242:
236:
228:
223:
219:
218:subproblems.
200:
196:
189:
166:
160:
152:
148:
127:
123:
116:
107:
105:
97:
95:
93:
92:
86:
84:
80:
76:
72:
68:
64:
59:
57:
53:
49:
45:
41:
34:
29:
21:
1222:
1216:
1206:
1179:
1175:
1165:
1140:
1136:
1126:
1101:
1097:
1087:
1060:
1054:
1044:
1019:
1015:
1005:
975:(1): 55–80.
972:
968:
958:
933:
929:
919:
884:
874:
847:
841:
831:
804:
800:
790:
770:
750:, retrieved
728:
718:
687:
680:
669:
665:
658:planar graph
651:
640:
552:
443:
345:
342:
330:
325:
278:
226:
224:
220:
150:
108:
103:
101:
89:
87:
70:
66:
60:
51:
47:
39:
38:
32:
1063:: 165–174.
850:(1): 1–11.
1255:Categories
752:2021-01-16
710:References
1241:0012-365X
1157:0020-0190
1118:0218-1959
1079:0012-365X
1036:0020-0190
989:1084-4309
950:0097-5397
866:0925-7721
823:0747-7171
563:Θ
496:−
473:−
454:Θ
387:−
295:−
698:See also
997:1645358
911:1499391
551:. When
102:In the
1239:
1194:
1155:
1116:
1077:
1034:
995:
987:
948:
909:
899:
864:
821:
778:
743:
33:cannot
993:S2CID
907:S2CID
656:of a
431:Knuth
69:or a
1237:ISSN
1192:ISBN
1180:5092
1153:ISSN
1114:ISSN
1075:ISSN
1032:ISSN
985:ISSN
946:ISSN
897:ISBN
862:ISSN
819:ISSN
776:ISBN
741:ISBN
662:face
1227:doi
1223:309
1184:doi
1145:doi
1141:109
1106:doi
1065:doi
1061:331
1024:doi
977:doi
938:doi
889:doi
852:doi
809:doi
733:doi
442:In
1257::
1235:.
1221:.
1215:.
1190:.
1174:.
1151:.
1139:.
1135:.
1112:.
1102:19
1100:.
1096:.
1073:.
1059:.
1053:.
1030:.
1020:98
1018:.
1014:.
991:.
983:.
971:.
967:.
944:.
934:28
932:.
928:.
905:.
895:.
883:.
860:.
846:.
840:.
817:.
803:.
799:.
760:^
739:,
727:,
652:A
58:.
1243:.
1229::
1200:.
1186::
1159:.
1147::
1120:.
1108::
1081:.
1067::
1038:.
1026::
999:.
979::
973:8
952:.
940::
913:.
891::
868:.
854::
848:4
825:.
811::
805:7
784:.
735::
688:d
670:k
666:k
636:.
623:)
616:2
612:/
608:3
604:n
597:n
593:)
587:2
582:2
579:+
576:3
573:(
567:(
553:d
538:)
531:2
527:/
523:3
519:n
512:n
508:)
502:)
499:1
493:d
490:(
487:d
482:2
479:+
476:1
470:d
467:2
464:(
458:(
444:d
437:.
416:)
409:2
405:/
401:3
397:n
390:3
384:n
381:5
377:2
373:!
370:n
364:(
360:O
326:d
312:d
308:/
304:4
301:+
298:4
292:d
289:2
279:d
265:)
260:1
257:+
254:d
251:2
247:n
243:d
240:(
237:O
227:d
206:)
201:4
197:n
193:(
190:O
170:)
167:n
164:(
161:O
133:)
128:5
124:n
120:(
117:O
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.