176:
2077:- an assignment of a weight in to each edge, such that the sum of weights near each vertex is at most 1 (an integral matching is a special case of a fractional matching in which the weights are in {0,1}). Similarly we define a fractional vertex-cover - an assignment of a non-negative weight to each vertex, such that the sum of weights in each edge is at least 1 (an integral vertex-cover is a special case of a fractional vertex-cover in which the weights are in {0,1}).
42:
2711:, so a minimum vertex cover is complementary to a maximum independent set; finding maximum independent sets is another NP-complete problem. The equivalence between matching and covering articulated in Kőnig's theorem allows minimum vertex covers and maximum independent sets to be computed in polynomial time for bipartite graphs, despite the NP-completeness of these problems for more general graph families.
162:
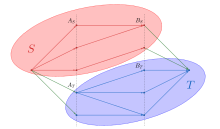
of every other edge), so this is a minimum vertex cover. Similarly, there can be no larger matching, because any matched edge has to include at least one endpoint in the vertex cover, so this is a maximum matching. Kőnig's theorem states that the equality between the sizes of the matching and the cover (in this example, both numbers are six) applies more generally to any bipartite graph.
2004:
must also be matched, for if there existed an alternating path to an unmatched vertex then changing the matching by removing the matched edges from this path and adding the unmatched edges in their place would increase the size of the matching. However, no matched edge can have both of its endpoints
161:
The bipartite graph shown in the above illustration has 14 vertices; a matching with six edges is shown in blue, and a vertex cover with six vertices is shown in red. There can be no smaller vertex cover, because any vertex cover has to include at least one endpoint of each matched edge (as well as
2817:
A graph is perfect if and only if its complement is perfect, and Kőnig's theorem can be seen as equivalent to the statement that the complement of a bipartite graph is perfect. For, each color class in a coloring of the complement of a bipartite graph is of size at most 2 and the classes of size 2
2348:
is a vector of size |V| in which each element represents the weight of a vertex in the fractional cover. Here, the first line is the size of the cover, the second line represents the non-negativity of the weights, and the third line represents the requirement that the sum of weights near each edge
2814:. Any bipartite graph is perfect, because each of its subgraphs is either bipartite or independent; in a bipartite graph that is not independent the chromatic number and the size of the largest clique are both two while in an independent set the chromatic number and clique number are both one.
3183:
As in the proof of Konig's theorem, the LP duality theorem implies that the optimal values are equal (for any graph), and the fact that the graph is bipartite implies that these programs have optimal solutions in which all values are integers.
2937:
sharing a common endpoint. Now Kőnig's line coloring theorem, stating that the chromatic index equals the maximum vertex degree in any bipartite graph, can be interpreted as stating that the line graph of a bipartite graph is perfect.
2445:
to be the set of vertices in the top layer of the diagram. From left to right label the vertices in the bottom layer with the numbers 1, …, 7 and label the vertices in the top layer with the numbers 8, …, 14. The set
116:
It is obvious from the definition that any vertex-cover set must be at least as large as any matching set (since for every edge in the matching, at least one vertex is needed in the cover). In particular, the
2363:
What makes bipartite graphs special is that, in bipartite graphs, both these linear programs have optimal solutions in which all variable values are integers. This follows from the fact that in the
2696:
For graphs that are not bipartite, the minimum vertex cover may be larger than the maximum matching. Moreover, the two problems are very different in complexity: maximum matchings can be found in
1698:
2353:
of the maximum fractional matching LP. Therefore, by the LP duality theorem, both programs have the same solution. This fact is true not only in bipartite graphs but in arbitrary graphs:
2574:
2686:
2624:
979:
933:
887:
841:
756:
722:
402:
239:
1435:
1230:
1190:
2367:
of a bipartite graph, all extreme points have only integer coordinates, and the same is true for the fractional vertex-cover polytope. Therefore the above theorem implies:
1936:
1827:
1803:
is matched but not in an alternating path, then its left endpoint cannot be in an alternating path (because two matched edges can not share a vertex) and thus belongs to
635:
2941:
Since line graphs of bipartite graphs are perfect, the complements of line graphs of bipartite graphs are also perfect. A clique in the complement of the line graph of
557:
2280:
2116:
2002:
280:
514:
488:
1392:
1365:
1338:
1311:
1284:
1257:
1127:
1100:
1053:
1026:
795:
209:
3449:
in Berlin and again at the Bled'07 International
Conference on Graph Theory, Harald Gropp has pointed out that the same result already appears in the language of
1533:
668:
306:
2524:
2504:
2484:
2464:
2443:
2423:
2063:
2043:
2023:
1976:
1956:
1910:
1887:
1867:
1847:
1801:
1781:
1761:
1741:
1721:
1636:
1616:
1596:
1576:
1556:
1503:
1483:
1455:
1073:
999:
688:
597:
577:
534:
462:
442:
422:
366:
346:
326:
2244:
so the third line indicates the constraint that the sum of weights near each vertex is at most 1. Similarly, the minimum fractional vertex-cover size in
3446:
1849:
is unmatched but not in an alternating path, then its left endpoint cannot be in an alternating path, for such a path could be extended by adding
2878:
vertices. Conversely, Kőnig's theorem proves the perfection of the complements of bipartite graphs, a result proven in a more explicit form by
35:
3832:
2965:. Therefore, Kőnig's theorem itself can also be interpreted as stating that the complements of line graphs of bipartite graphs are perfect.
2382:
The constructive proof described above provides an algorithm for producing a minimum vertex cover given a maximum matching. Thus, the
3911:
3892:
3866:
3654:
3624:
3576:
2386:
for finding maximum matchings in bipartite graphs may also be used to solve the vertex cover problem efficiently in these graphs.
3921:
1638:
by alternating paths (paths that alternate between edges that are in the matching and edges that are not in the matching). Let
3232:
is an assignment of a non-negative integral weight to each edge, such that the sum of weights of edges adjacent to any vertex
3783:
2708:
3566:
2961:
into subsets of edges sharing a common endpoint; the endpoints shared by each of these subsets form a vertex cover for
2383:
2506:
are 1–10–3–13–7, 1–10–3–11–5–13–7, 1–11–5–13–7, 1–11–5–10–3–13–7, and all subpaths of these starting from 1. The set
1644:
3669:
2775:
2389:
Despite the equivalence of the two problems from the point of view of exact solutions, they are not equivalent for
3926:
45:
An example of a bipartite graph, with a maximum matching (blue) and minimum vertex cover (red) both of size six.
3817:
Hypergraph
Seminar (Proc. First Working Sem., Ohio State Univ., Columbus, Ohio, 1972; dedicated to Arnold Ross)
3450:
2787:
2397:; in contrast, approximating the minimum vertex cover of a bipartite graph requires at least logarithmic time.
759:
3619:, Wiley Series in Discrete Mathematics and Optimization, vol. 33, John Wiley & Sons, pp. 48–49,
2735:
of any bipartite graph (that is, the minimum number of matchings into which it can be partitioned) equals its
2358:
In any graph, the largest size of a fractional matching equals the smallest size of a fractional vertex cover.
3698:
Göös, Mika; Suomela, Jukka (2014), "No sublogarithmic-time approximation scheme for bipartite vertex cover",
3916:
3283:
2529:
2390:
106:
3020:
is a multiset of vertices ("multiset" means that each vertex may appear several times), in which each edge
3606:
3586:
2858:| colors, which by the perfection of complements of bipartite graphs corresponds to an independent set in
2629:
2579:
938:
892:
3850:
3812:
3778:
101:
in a graph is a set of vertices that includes at least one endpoint of every edge, and a vertex cover is
3516:
2811:
2774:
Kőnig's theorem is equivalent to many other min-max theorems in graph theory and combinatorics, such as
2736:
2394:
2779:
846:
800:
244:
The following proof provides a way of constructing a minimum vertex cover from a maximum matching. Let
3243:. Egerváry's theorem can be extended, using a similar argument, to graphs that have both edge-weights
2783:
1400:
1195:
1135:
691:
148:
118:
74:
175:
3610:
3590:
2759:
2754:, Kőnig attributed the idea of studying matchings in bipartite graphs to his father, mathematician
2350:
2074:
17:
3032:
2988:
2981:
2372:
In any bipartite graph, the largest size of a matching equals the smallest size of a vertex cover.
1915:
1806:
731:
697:
377:
214:
82:
31:
27:
Theorem showing that maximum matching and minimum vertex cover are equivalent for bipartite graphs
3854:
3733:
3707:
2763:
602:
2885:
One can also connect Kőnig's line coloring theorem to a different class of perfect graphs, the
3888:
3862:
3828:
3761:
3744:
3650:
3620:
3572:
3433:
2720:
2364:
539:
62:
3614:
2393:. Bipartite maximum matchings can be approximated arbitrarily accurately in constant time by
2247:
2083:
1981:
247:
3820:
3792:
3717:
3678:
2807:
2803:
2728:
2237:
493:
467:
144:
122:
70:
3876:
3842:
3804:
3729:
3690:
1370:
1343:
1316:
1289:
1262:
1235:
1105:
1078:
1031:
1004:
768:
182:
3872:
3838:
3800:
3725:
3686:
3602:
2732:
2697:
140:
126:
78:
1508:
643:
285:
2216:| zeros, so the second line indicates the constraint that the weights are non-negative.
129:, the minimum vertex cover set and the maximum matching set have in fact the same size.
3643:
3638:
3454:
2974:
2755:
2509:
2489:
2469:
2449:
2428:
2408:
2119:
2048:
2028:
2008:
1961:
1941:
1895:
1872:
1852:
1832:
1786:
1766:
1746:
1726:
1706:
1621:
1601:
1581:
1561:
1541:
1488:
1468:
1440:
1058:
984:
673:
582:
562:
519:
447:
427:
407:
351:
331:
311:
86:
2192:| in which each element represents the weight of an edge in the fractional matching.
41:
3905:
3796:
2799:
2724:
2073:
To explain this proof, we first have to extend the notion of a matching to that of a
3737:
3819:, Lecture Notes in Mathematics, vol. 411, Berlin: Springer, pp. 111–126,
3664:
2762:, but his theorem is sometimes spelled (incorrectly) in German characters, with an
372:
98:
54:
109:
in a graph is a set of edges no two of which share an endpoint, and a matching is
3634:
2701:
725:
50:
3721:
2886:
3747:(1916), "Gráfok és alkalmazásuk a determinánsok és a halmazok elméletére",
2826:, and as we have already described an independent set in a bipartite graph
2723:. Kőnig had announced in 1914 and published in 1916 the results that every
2349:
must be at least 1. Now, the minimum fractional cover LP is exactly the
3824:
3682:
3408:, p 319, and for the connection to vertex cover see p. 342.
1505:
from being a matching in the first place), so if a vertex cover with
1232:
is a vertex cover, as any edge that is not incident to vertices from
3013:
is the sum of weights of the edges participating in the matching. A
3887:, Progress in Computer Science and Applied Logic Series, Springer,
2747:
attribute Kőnig's theorem itself to a later paper of Kőnig (1931).
1743:
either belongs to an alternating path (and has a right endpoint in
3712:
3490:
3341:
3256:
In any edge-weighted vertex-weighted bipartite graph, the maximum
1340:, which would contradict the fact that there are no edges between
174:
40:
3044:
weight of a matching equals the smallest number of vertices in a
2425:
to be the set of vertices in the bottom layer of the diagram and
3861:, Annals of Discrete Mathematics, vol. 29, North-Holland,
3781:(1972), "Normal hypergraphs and the perfect graph conjecture",
3545:
3543:
2203:| ones, so the first line indicates the size of the matching.
1465:
No vertex in a vertex cover can cover more than one edge of
981:. Then the minimum cut is composed only of edges going from
2719:
Kőnig's theorem is named after the
Hungarian mathematician
1978:, the set of unmatched left vertices. And every vertex in
1535:
vertices can be constructed, it must be a minimum cover.
2949:. And a coloring in the complement of the line graph of
2846:
vertices corresponds to a coloring of the complement of
2818:
form a matching, a clique in the complement of a graph
1912:
is an endpoint of a matched edge. For, every vertex in
3530:
3528:
2632:
2582:
2532:
2512:
2492:
2472:
2452:
2431:
2411:
2250:
2086:
2051:
2031:
2011:
1984:
1964:
1944:
1918:
1898:
1875:
1855:
1835:
1809:
1789:
1769:
1749:
1729:
1709:
1647:
1624:
1604:
1584:
1564:
1544:
1511:
1491:
1471:
1443:
1403:
1373:
1346:
1319:
1292:
1265:
1238:
1198:
1138:
1108:
1081:
1061:
1034:
1007:
987:
941:
895:
849:
803:
771:
734:
700:
676:
646:
605:
585:
565:
542:
522:
496:
470:
450:
430:
410:
380:
354:
334:
314:
288:
250:
217:
185:
3059:
weight of a fractional matching is given by the LP:
2707:
The complement of a vertex cover in any graph is an
81:. It was discovered independently, also in 1931, by
3118:And the minimum number of vertices in a fractional
2870:| vertices, which corresponds to a vertex cover of
1132:Therefore, the size of the minimum cut is equal to
3642:
3040:In any edge-weighted bipartite graph, the maximum
2680:
2618:
2568:
2518:
2498:
2478:
2458:
2437:
2417:
2274:
2110:
2057:
2037:
2017:
1996:
1970:
1950:
1930:
1904:
1881:
1861:
1841:
1821:
1795:
1775:
1755:
1735:
1715:
1692:
1630:
1610:
1590:
1570:
1550:
1527:
1497:
1477:
1449:
1429:
1386:
1359:
1332:
1305:
1278:
1251:
1224:
1184:
1121:
1094:
1067:
1047:
1020:
993:
973:
927:
881:
835:
789:
750:
716:
682:
662:
629:
591:
571:
551:
528:
508:
482:
456:
436:
416:
396:
360:
340:
320:
300:
274:
233:
203:
3885:An Introduction to Data Structures and Algorithms
3670:Acta Mathematica Academiae Scientiarum Hungaricae
2905:, and an edge for each pair of adjacent edges in
3466:
2980:
2782:. Since bipartite matching is a special case of
2751:
2080:The maximum fractional matching size in a graph
1693:{\displaystyle K=(A\setminus Z)\cup (B\cap Z).}
105:if no other vertex cover has fewer vertices. A
3667:(1958), "Maximum-minimum Sätze über Graphen",
3192:One can consider a graph in which each vertex
2526:is therefore {1,3,5,7,10,11,13}, resulting in
3571:, Oxford University Press, pp. 203–207,
3549:
3478:
3392:
2957:is bipartite, is a partition of the edges of
2700:for any graph, while minimum vertex cover is
1485:(because the edge half-overlap would prevent
424:in such way that there are edges of capacity
8:
3815:(1974), "Minimax theorems for hypergraphs",
3353:
2991:(1931) considered graphs in which each edge
2675:
2639:
2613:
2595:
2563:
2545:
2486:is {1}. The alternating paths starting from
2405:In the graph shown in the introduction take
1286:must be incident to a pair of vertices from
3565:Biggs, E. K.; Lloyd; Wilson, R. J. (1976),
3417:
30:For the theorem about infinite graphs, see
3749:Matematikai és Természettudományi Értesítő
3592:Matchings and the max-flow min-cut theorem
3380:
3376:
3374:
3365:
3337:
3333:
3331:
3322:
3310:
2744:
2045:is a vertex cover of cardinality equal to
1598:be the set of vertices that are either in
3711:
2631:
2581:
2531:
2511:
2491:
2471:
2451:
2430:
2410:
2249:
2085:
2050:
2030:
2010:
1983:
1963:
1943:
1917:
1897:
1874:
1854:
1834:
1808:
1788:
1768:
1748:
1728:
1708:
1646:
1623:
1603:
1583:
1563:
1543:
1520:
1512:
1510:
1490:
1470:
1442:
1421:
1408:
1402:
1378:
1372:
1351:
1345:
1324:
1318:
1297:
1291:
1270:
1264:
1243:
1237:
1216:
1203:
1197:
1177:
1171:
1162:
1154:
1148:
1139:
1137:
1129:would make the size of the cut infinite.
1113:
1107:
1086:
1080:
1060:
1039:
1033:
1012:
1006:
986:
959:
946:
940:
913:
900:
894:
873:
860:
848:
827:
814:
802:
770:
739:
733:
705:
699:
675:
655:
647:
645:
604:
584:
564:
541:
521:
495:
469:
449:
429:
409:
385:
379:
353:
333:
313:
287:
249:
222:
216:
184:
125:set. Kőnig's theorem states that, in any
3447:International Congress of Mathematicians
1461:Constructive proof without flow concepts
69:), describes an equivalence between the
3294:
2536:
1922:
1813:
1660:
3534:
3520:
3503:
3429:
3405:
2879:
2569:{\displaystyle L\setminus Z=\{2,4,6\}}
2069:Proof using linear programming duality
2065:, and must be a minimum vertex cover.
3124:vertex-cover is given by the dual LP:
2830:is a complement of a vertex cover in
113:if no other matching has more edges.
66:
7:
2786:, the theorem also results from the
2681:{\displaystyle K=\{2,4,6,10,11,13\}}
2619:{\displaystyle R\cap Z=\{10,11,13\}}
2282:is the solution of the following LP:
1558:be the set of unmatched vertices in
974:{\displaystyle A_{T},B_{T}\subset T}
928:{\displaystyle A_{S},B_{S}\subset S}
2984:'s theorem for edge-weighted graphs
2973:Konig's theorem can be extended to
2933:) are exactly the sets of edges in
2758:. In Hungarian, Kőnig's name has a
2739:– the latter statement is known as
724:, which, in turn, is the size of a
308:be the two parts of the vertex set
147:equals the number of vertices in a
18:König's theorem (graph theory)
3445:In a poster displayed at the 1998
3203:. The weight vector is denoted by
3196:has a non-negative integer weight
3188:Theorem for vertex-weighted graphs
3002:. The weight vector is denoted by
2995:has a non-negative integer weight
740:
706:
546:
386:
223:
25:
2118:is the solution of the following
882:{\displaystyle B=B_{S}\cup B_{T}}
836:{\displaystyle A=A_{S}\cup A_{T}}
3467:Biggs, Lloyd & Wilson (1976)
3340:, Theorem 5.3, p. 74;
3214:of a vertex-cover is the sum of
2917:) equals the chromatic index of
2909:. Thus, the chromatic number of
2901:) has a vertex for each edge of
2752:Biggs, Lloyd & Wilson (1976)
1763:), or it has a left endpoint in
121:set is at least as large as the
36:König's theorem (disambiguation)
3284:Kőnig's property in hypergraphs
2810:equals the size of the largest
2794:Connections with perfect graphs
1538:To construct such a cover, let
1430:{\displaystyle A_{T}\cup B_{S}}
1225:{\displaystyle A_{T}\cup B_{S}}
1185:{\displaystyle |A_{T}|+|B_{S}|}
3764:(1931), "Gráfok és mátrixok",
3645:Graph Theory with Applications
3434:Exercise 261, p. 342
2731:, and more generally that the
2626:and the minimum vertex cover
2269:
2257:
2105:
2093:
1892:Additionally, every vertex in
1684:
1672:
1666:
1654:
1521:
1513:
1178:
1163:
1155:
1140:
784:
772:
656:
648:
618:
606:
269:
257:
198:
186:
1:
3264:-matching equals the minimum
2925:is bipartite, the cliques in
2741:Kőnig's line coloring theorem
1437:is a minimum vertex cover of
282:be a bipartite graph and let
3797:10.1016/0012-365X(72)90006-4
3766:Matematikai és Fizikai Lapok
3481:, Theorem 1.4.17, pp. 37ff..
2365:fractional matching polytope
1931:{\displaystyle A\setminus Z}
1822:{\displaystyle A\setminus Z}
751:{\displaystyle G'_{\infty }}
717:{\displaystyle G'_{\infty }}
397:{\displaystyle G'_{\infty }}
234:{\displaystyle G'_{\infty }}
85:in the more general case of
3550:Lovász & Plummer (1986)
3479:Lovász & Plummer (1986)
3393:Lovász & Plummer (1986)
2893:is a graph, the line graph
2466:of unmatched vertices from
670:of the maximum matching in
143:, the number of edges in a
3943:
3616:Combinatorial Optimization
3605:; Cunningham, William H.;
3502:"Trivially", according to
1578:(possibly empty), and let
630:{\displaystyle (a,b)\in E}
348:is a maximum matching for
29:
3722:10.1007/s00446-013-0194-z
3418:Göös & Suomela (2014)
3268:-weight of vertices in a
2822:is an independent set in
3912:Theorems in graph theory
3404:For this algorithm, see
3381:Bondy & Murty (1976)
3368:, Lemma 5.3, p. 74.
3366:Bondy & Murty (1976)
3338:Bondy & Murty (1976)
3323:Bondy & Murty (1976)
3311:Bondy & Murty (1976)
3024:is adjacent to at least
2889:of bipartite graphs. If
2788:max-flow min-cut theorem
2745:Bondy & Murty (1976)
2391:approximation algorithms
760:max-flow min-cut theorem
552:{\displaystyle +\infty }
133:Statement of the theorem
73:problem and the minimum
3922:Matching (graph theory)
3607:Pulleyblank, William R.
2776:Hall's marriage theorem
2384:Hopcroft–Karp algorithm
2275:{\displaystyle G=(V,E)}
2111:{\displaystyle G=(V,E)}
1997:{\displaystyle B\cap Z}
275:{\displaystyle G=(V,E)}
3883:Storer, J. A. (2001),
3568:Graph Theory 1736–1936
3453:in the 1894 thesis of
3275:
3181:
3116:
3051:
2945:is just a matching in
2798:A graph is said to be
2727:bipartite graph has a
2682:
2620:
2570:
2520:
2500:
2480:
2460:
2439:
2419:
2395:distributed algorithms
2375:
2361:
2342:
2276:
2182:
2112:
2059:
2039:
2019:
1998:
1972:
1952:
1932:
1906:
1889:forms a vertex cover.
1883:
1863:
1843:
1823:
1797:
1777:
1757:
1737:
1717:
1694:
1632:
1612:
1592:
1572:
1552:
1529:
1499:
1479:
1451:
1431:
1388:
1361:
1334:
1307:
1280:
1253:
1226:
1186:
1123:
1096:
1069:
1049:
1022:
995:
975:
929:
883:
837:
797:be a minimum cut. Let
791:
758:, as follows from the
752:
718:
684:
664:
631:
593:
573:
553:
530:
510:
509:{\displaystyle b\in B}
490:and from every vertex
484:
483:{\displaystyle a\in A}
458:
438:
418:
398:
362:
342:
322:
302:
276:
241:
235:
205:
154:
46:
34:. For other uses, see
3700:Distributed Computing
3517:perfect graph theorem
3253:
3126:
3061:
3037:
2838:in a bipartite graph
2834:. Thus, any matching
2683:
2621:
2571:
2521:
2501:
2481:
2461:
2440:
2420:
2369:
2355:
2284:
2277:
2188:is a vector of size |
2124:
2113:
2060:
2040:
2020:
1999:
1973:
1953:
1933:
1907:
1884:
1864:
1844:
1824:
1798:
1778:
1758:
1738:
1718:
1695:
1633:
1613:
1593:
1573:
1553:
1530:
1500:
1480:
1452:
1432:
1389:
1387:{\displaystyle B_{T}}
1362:
1360:{\displaystyle A_{S}}
1335:
1333:{\displaystyle B_{T}}
1308:
1306:{\displaystyle A_{S}}
1281:
1279:{\displaystyle B_{S}}
1254:
1252:{\displaystyle A_{T}}
1227:
1192:. On the other hand,
1187:
1124:
1122:{\displaystyle B_{T}}
1097:
1095:{\displaystyle A_{S}}
1070:
1050:
1048:{\displaystyle B_{S}}
1023:
1021:{\displaystyle A_{T}}
996:
976:
930:
884:
838:
792:
790:{\displaystyle (S,T)}
753:
719:
685:
665:
632:
594:
574:
554:
531:
511:
485:
459:
439:
419:
399:
363:
343:
323:
303:
277:
236:
206:
204:{\displaystyle (S,T)}
178:
136:
44:
3784:Discrete Mathematics
3611:Schrijver, Alexander
3587:Cesa-Bianchi, Nicolò
3011:weight of a matching
2692:Non-bipartite graphs
2630:
2580:
2530:
2510:
2490:
2470:
2450:
2429:
2409:
2248:
2084:
2049:
2029:
2009:
1982:
1962:
1942:
1916:
1896:
1873:
1853:
1833:
1829:. Alternatively, if
1807:
1787:
1767:
1747:
1727:
1707:
1645:
1622:
1618:or are connected to
1602:
1582:
1562:
1542:
1509:
1489:
1469:
1441:
1401:
1371:
1344:
1317:
1290:
1263:
1236:
1196:
1136:
1106:
1079:
1059:
1032:
1005:
985:
939:
893:
847:
801:
769:
732:
698:
674:
644:
603:
583:
563:
540:
520:
494:
468:
448:
428:
408:
378:
352:
332:
312:
286:
248:
215:
211:in the flow network
183:
149:minimum vertex cover
119:minimum vertex cover
75:vertex cover problem
3354:Cesa-Bianchi (2020)
3247:and vertex-weights
2760:double acute accent
2351:dual linear program
2075:fractional matching
1938:is matched because
1528:{\displaystyle |M|}
1075:, as any edge from
747:
713:
663:{\displaystyle |M|}
393:
301:{\displaystyle A,B}
230:
3825:10.1007/BFb0066186
3683:10.1007/BF02020271
3589:(April 11, 2020),
3491:Cook et al. (2011)
3342:Cook et al. (2011)
2780:Dilworth's theorem
2678:
2616:
2566:
2516:
2496:
2476:
2456:
2435:
2415:
2272:
2108:
2055:
2035:
2015:
1994:
1968:
1948:
1928:
1902:
1879:
1859:
1839:
1819:
1793:
1773:
1753:
1733:
1713:
1690:
1628:
1608:
1588:
1568:
1548:
1525:
1495:
1475:
1447:
1427:
1384:
1357:
1330:
1303:
1276:
1249:
1222:
1182:
1119:
1092:
1065:
1045:
1018:
991:
971:
925:
879:
833:
787:
748:
735:
714:
701:
680:
660:
627:
589:
569:
549:
536:, and of capacity
526:
506:
480:
454:
434:
414:
394:
381:
358:
338:
318:
298:
272:
242:
231:
218:
201:
171:Constructive proof
47:
3834:978-3-540-06846-4
3649:, North Holland,
3383:, pp. 74–75.
2969:Weighted variants
2519:{\displaystyle Z}
2499:{\displaystyle U}
2479:{\displaystyle L}
2459:{\displaystyle U}
2438:{\displaystyle R}
2418:{\displaystyle L}
2058:{\displaystyle M}
2038:{\displaystyle K}
2018:{\displaystyle K}
1971:{\displaystyle U}
1958:is a superset of
1951:{\displaystyle Z}
1905:{\displaystyle K}
1882:{\displaystyle K}
1862:{\displaystyle e}
1842:{\displaystyle e}
1796:{\displaystyle e}
1776:{\displaystyle K}
1756:{\displaystyle K}
1736:{\displaystyle E}
1716:{\displaystyle e}
1631:{\displaystyle U}
1611:{\displaystyle U}
1591:{\displaystyle Z}
1571:{\displaystyle A}
1551:{\displaystyle U}
1498:{\displaystyle M}
1478:{\displaystyle M}
1450:{\displaystyle G}
1068:{\displaystyle t}
994:{\displaystyle s}
690:is the size of a
683:{\displaystyle G}
592:{\displaystyle b}
572:{\displaystyle a}
529:{\displaystyle t}
457:{\displaystyle s}
437:{\displaystyle 1}
417:{\displaystyle G}
361:{\displaystyle G}
341:{\displaystyle M}
321:{\displaystyle V}
16:(Redirected from
3934:
3927:Bipartite graphs
3897:
3879:
3845:
3807:
3773:
3756:
3740:
3715:
3693:
3677:(3–4): 395–434,
3659:
3648:
3629:
3603:Cook, William J.
3598:
3597:
3581:
3553:
3547:
3538:
3532:
3523:
3513:
3507:
3500:
3494:
3488:
3482:
3476:
3470:
3464:
3458:
3443:
3437:
3427:
3421:
3415:
3409:
3402:
3396:
3390:
3384:
3378:
3369:
3363:
3357:
3351:
3345:
3335:
3326:
3320:
3314:
3309:respectively by
3307:minimum covering
3299:
3225:in the cover. A
3145:Subject to:
3077:Subject to:
3035:'s theorem says:
2808:chromatic number
2804:induced subgraph
2770:Related theorems
2729:perfect matching
2687:
2685:
2684:
2679:
2625:
2623:
2622:
2617:
2575:
2573:
2572:
2567:
2525:
2523:
2522:
2517:
2505:
2503:
2502:
2497:
2485:
2483:
2482:
2477:
2465:
2463:
2462:
2457:
2444:
2442:
2441:
2436:
2424:
2422:
2421:
2416:
2303:Subject to:
2281:
2279:
2278:
2273:
2238:incidence matrix
2223:is a vector of |
2212:is a vector of |
2199:is a vector of |
2143:Subject to:
2117:
2115:
2114:
2109:
2064:
2062:
2061:
2056:
2044:
2042:
2041:
2036:
2024:
2022:
2021:
2016:
2003:
2001:
2000:
1995:
1977:
1975:
1974:
1969:
1957:
1955:
1954:
1949:
1937:
1935:
1934:
1929:
1911:
1909:
1908:
1903:
1888:
1886:
1885:
1880:
1868:
1866:
1865:
1860:
1848:
1846:
1845:
1840:
1828:
1826:
1825:
1820:
1802:
1800:
1799:
1794:
1782:
1780:
1779:
1774:
1762:
1760:
1759:
1754:
1742:
1740:
1739:
1734:
1722:
1720:
1719:
1714:
1699:
1697:
1696:
1691:
1637:
1635:
1634:
1629:
1617:
1615:
1614:
1609:
1597:
1595:
1594:
1589:
1577:
1575:
1574:
1569:
1557:
1555:
1554:
1549:
1534:
1532:
1531:
1526:
1524:
1516:
1504:
1502:
1501:
1496:
1484:
1482:
1481:
1476:
1456:
1454:
1453:
1448:
1436:
1434:
1433:
1428:
1426:
1425:
1413:
1412:
1393:
1391:
1390:
1385:
1383:
1382:
1366:
1364:
1363:
1358:
1356:
1355:
1339:
1337:
1336:
1331:
1329:
1328:
1312:
1310:
1309:
1304:
1302:
1301:
1285:
1283:
1282:
1277:
1275:
1274:
1258:
1256:
1255:
1250:
1248:
1247:
1231:
1229:
1228:
1223:
1221:
1220:
1208:
1207:
1191:
1189:
1188:
1183:
1181:
1176:
1175:
1166:
1158:
1153:
1152:
1143:
1128:
1126:
1125:
1120:
1118:
1117:
1101:
1099:
1098:
1093:
1091:
1090:
1074:
1072:
1071:
1066:
1054:
1052:
1051:
1046:
1044:
1043:
1027:
1025:
1024:
1019:
1017:
1016:
1000:
998:
997:
992:
980:
978:
977:
972:
964:
963:
951:
950:
934:
932:
931:
926:
918:
917:
905:
904:
888:
886:
885:
880:
878:
877:
865:
864:
842:
840:
839:
834:
832:
831:
819:
818:
796:
794:
793:
788:
757:
755:
754:
749:
743:
723:
721:
720:
715:
709:
689:
687:
686:
681:
669:
667:
666:
661:
659:
651:
636:
634:
633:
628:
598:
596:
595:
590:
578:
576:
575:
570:
558:
556:
555:
550:
535:
533:
532:
527:
515:
513:
512:
507:
489:
487:
486:
481:
464:to every vertex
463:
461:
460:
455:
444:from the source
443:
441:
440:
435:
423:
421:
420:
415:
403:
401:
400:
395:
389:
367:
365:
364:
359:
347:
345:
344:
339:
328:. Suppose that
327:
325:
324:
319:
307:
305:
304:
299:
281:
279:
278:
273:
240:
238:
237:
232:
226:
210:
208:
207:
202:
145:maximum matching
123:maximum matching
79:bipartite graphs
71:maximum matching
21:
3942:
3941:
3937:
3936:
3935:
3933:
3932:
3931:
3902:
3901:
3895:
3882:
3869:
3859:Matching Theory
3849:
3835:
3811:
3777:
3760:
3743:
3697:
3663:
3657:
3639:Murty, U. S. R.
3633:
3627:
3601:
3595:
3585:
3579:
3564:
3561:
3556:
3548:
3541:
3533:
3526:
3514:
3510:
3501:
3497:
3489:
3485:
3477:
3473:
3465:
3461:
3444:
3440:
3428:
3424:
3416:
3412:
3403:
3399:
3391:
3387:
3379:
3372:
3364:
3360:
3352:
3348:
3336:
3329:
3321:
3317:
3300:
3296:
3292:
3280:
3241:
3219:
3201:
3190:
3168:
3156:
3136:
3112:
3100:
3088:
3029:
3000:
2986:
2975:weighted graphs
2971:
2796:
2772:
2733:chromatic index
2717:
2709:independent set
2698:polynomial time
2694:
2628:
2627:
2578:
2577:
2528:
2527:
2508:
2507:
2488:
2487:
2468:
2467:
2448:
2447:
2427:
2426:
2407:
2406:
2403:
2380:
2338:
2326:
2314:
2294:
2246:
2245:
2235:
2222:
2210:
2198:
2178:
2166:
2154:
2134:
2082:
2081:
2071:
2047:
2046:
2027:
2026:
2007:
2006:
1980:
1979:
1960:
1959:
1940:
1939:
1914:
1913:
1894:
1893:
1871:
1870:
1851:
1850:
1831:
1830:
1805:
1804:
1785:
1784:
1765:
1764:
1745:
1744:
1725:
1724:
1705:
1704:
1643:
1642:
1620:
1619:
1600:
1599:
1580:
1579:
1560:
1559:
1540:
1539:
1507:
1506:
1487:
1486:
1467:
1466:
1463:
1439:
1438:
1417:
1404:
1399:
1398:
1374:
1369:
1368:
1347:
1342:
1341:
1320:
1315:
1314:
1293:
1288:
1287:
1266:
1261:
1260:
1239:
1234:
1233:
1212:
1199:
1194:
1193:
1167:
1144:
1134:
1133:
1109:
1104:
1103:
1082:
1077:
1076:
1057:
1056:
1035:
1030:
1029:
1008:
1003:
1002:
983:
982:
955:
942:
937:
936:
909:
896:
891:
890:
869:
856:
845:
844:
823:
810:
799:
798:
767:
766:
730:
729:
728:in the network
696:
695:
672:
671:
642:
641:
601:
600:
581:
580:
561:
560:
538:
537:
518:
517:
492:
491:
466:
465:
446:
445:
426:
425:
406:
405:
376:
375:
350:
349:
330:
329:
310:
309:
284:
283:
246:
245:
213:
212:
181:
180:
173:
168:
159:
141:bipartite graph
135:
127:bipartite graph
95:
87:weighted graphs
63:Dénes Kőnig
59:Kőnig's theorem
39:
28:
23:
22:
15:
12:
11:
5:
3940:
3938:
3930:
3929:
3924:
3919:
3917:Perfect graphs
3914:
3904:
3903:
3900:
3899:
3893:
3880:
3867:
3855:Plummer, M. D.
3851:Lovász, László
3847:
3833:
3813:Lovász, László
3809:
3791:(3): 253–267,
3779:Lovász, László
3775:
3758:
3741:
3706:(6): 435–443,
3695:
3661:
3655:
3631:
3625:
3599:
3583:
3577:
3560:
3557:
3555:
3554:
3552:, p. 271.
3539:
3524:
3508:
3495:
3483:
3471:
3459:
3455:Ernst Steinitz
3451:configurations
3438:
3422:
3410:
3397:
3395:, p. 270.
3385:
3370:
3358:
3346:
3327:
3315:
3293:
3291:
3288:
3287:
3286:
3279:
3276:
3239:
3217:
3199:
3189:
3186:
3164:
3154:
3132:
3128:Minimize
3110:
3096:
3086:
3063:Maximize
3027:
2998:
2985:
2979:
2970:
2967:
2795:
2792:
2771:
2768:
2737:maximum degree
2716:
2713:
2693:
2690:
2677:
2674:
2671:
2668:
2665:
2662:
2659:
2656:
2653:
2650:
2647:
2644:
2641:
2638:
2635:
2615:
2612:
2609:
2606:
2603:
2600:
2597:
2594:
2591:
2588:
2585:
2565:
2562:
2559:
2556:
2553:
2550:
2547:
2544:
2541:
2538:
2535:
2515:
2495:
2475:
2455:
2434:
2414:
2402:
2399:
2379:
2376:
2336:
2322:
2312:
2290:
2286:Minimize
2271:
2268:
2265:
2262:
2259:
2256:
2253:
2231:
2220:
2208:
2196:
2176:
2162:
2152:
2130:
2126:Maximize
2120:linear program
2107:
2104:
2101:
2098:
2095:
2092:
2089:
2070:
2067:
2054:
2034:
2014:
1993:
1990:
1987:
1967:
1947:
1927:
1924:
1921:
1901:
1878:
1858:
1838:
1818:
1815:
1812:
1792:
1772:
1752:
1732:
1712:
1701:
1700:
1689:
1686:
1683:
1680:
1677:
1674:
1671:
1668:
1665:
1662:
1659:
1656:
1653:
1650:
1627:
1607:
1587:
1567:
1547:
1523:
1519:
1515:
1494:
1474:
1462:
1459:
1446:
1424:
1420:
1416:
1411:
1407:
1381:
1377:
1354:
1350:
1327:
1323:
1300:
1296:
1273:
1269:
1246:
1242:
1219:
1215:
1211:
1206:
1202:
1180:
1174:
1170:
1165:
1161:
1157:
1151:
1147:
1142:
1116:
1112:
1089:
1085:
1064:
1042:
1038:
1015:
1011:
990:
970:
967:
962:
958:
954:
949:
945:
924:
921:
916:
912:
908:
903:
899:
876:
872:
868:
863:
859:
855:
852:
830:
826:
822:
817:
813:
809:
806:
786:
783:
780:
777:
774:
746:
742:
738:
712:
708:
704:
679:
658:
654:
650:
626:
623:
620:
617:
614:
611:
608:
588:
568:
548:
545:
525:
505:
502:
499:
479:
476:
473:
453:
433:
413:
392:
388:
384:
371:Construct the
357:
337:
317:
297:
294:
291:
271:
268:
265:
262:
259:
256:
253:
229:
225:
221:
200:
197:
194:
191:
188:
172:
169:
167:
164:
158:
155:
134:
131:
94:
91:
26:
24:
14:
13:
10:
9:
6:
4:
3:
2:
3939:
3928:
3925:
3923:
3920:
3918:
3915:
3913:
3910:
3909:
3907:
3896:
3894:9780817642532
3890:
3886:
3881:
3878:
3874:
3870:
3868:0-444-87916-1
3864:
3860:
3856:
3852:
3848:
3844:
3840:
3836:
3830:
3826:
3822:
3818:
3814:
3810:
3806:
3802:
3798:
3794:
3790:
3786:
3785:
3780:
3776:
3771:
3767:
3763:
3759:
3754:
3750:
3746:
3742:
3739:
3735:
3731:
3727:
3723:
3719:
3714:
3709:
3705:
3701:
3696:
3692:
3688:
3684:
3680:
3676:
3672:
3671:
3666:
3665:Gallai, Tibor
3662:
3658:
3656:0-444-19451-7
3652:
3647:
3646:
3640:
3636:
3632:
3628:
3626:9781118031391
3622:
3618:
3617:
3612:
3608:
3604:
3600:
3594:
3593:
3588:
3584:
3580:
3578:0-19-853916-9
3574:
3570:
3569:
3563:
3562:
3558:
3551:
3546:
3544:
3540:
3536:
3535:Lovász (1974)
3531:
3529:
3525:
3522:
3521:Lovász (1972)
3518:
3512:
3509:
3505:
3504:Lovász (1974)
3499:
3496:
3492:
3487:
3484:
3480:
3475:
3472:
3468:
3463:
3460:
3456:
3452:
3448:
3442:
3439:
3435:
3431:
3430:Storer (2001)
3426:
3423:
3419:
3414:
3411:
3407:
3406:Storer (2001)
3401:
3398:
3394:
3389:
3386:
3382:
3377:
3375:
3371:
3367:
3362:
3359:
3355:
3350:
3347:
3343:
3339:
3334:
3332:
3328:
3325:, p. 70.
3324:
3319:
3316:
3313:, p. 73.
3312:
3308:
3304:
3298:
3295:
3289:
3285:
3282:
3281:
3277:
3274:
3273:
3272:vertex-cover.
3271:
3267:
3263:
3259:
3252:
3250:
3246:
3242:
3235:
3231:
3229:
3224:
3220:
3213:
3211:
3206:
3202:
3195:
3187:
3185:
3180:
3179:
3177:
3172:
3167:
3163:
3158:
3157:
3152:
3148:
3143:
3142:
3139:
3135:
3131:
3125:
3123:
3122:
3115:
3114:
3109:
3104:
3099:
3095:
3090:
3089:
3084:
3080:
3075:
3074:
3071:
3068:
3067:
3060:
3058:
3057:
3050:
3049:
3048:vertex-cover.
3047:
3043:
3036:
3034:
3030:
3023:
3019:
3017:
3012:
3009:
3005:
3001:
2994:
2990:
2989:Jenő Egerváry
2983:
2978:
2976:
2968:
2966:
2964:
2960:
2956:
2952:
2948:
2944:
2939:
2936:
2932:
2928:
2924:
2920:
2916:
2912:
2908:
2904:
2900:
2896:
2892:
2888:
2883:
2881:
2880:Gallai (1958)
2877:
2873:
2869:
2865:
2861:
2857:
2853:
2849:
2845:
2841:
2837:
2833:
2829:
2825:
2821:
2815:
2813:
2809:
2805:
2802:if, in every
2801:
2793:
2791:
2789:
2785:
2781:
2777:
2769:
2767:
2765:
2761:
2757:
2753:
2750:According to
2748:
2746:
2742:
2738:
2734:
2730:
2726:
2722:
2714:
2712:
2710:
2705:
2703:
2699:
2691:
2689:
2672:
2669:
2666:
2663:
2660:
2657:
2654:
2651:
2648:
2645:
2642:
2636:
2633:
2610:
2607:
2604:
2601:
2598:
2592:
2589:
2586:
2583:
2560:
2557:
2554:
2551:
2548:
2542:
2539:
2533:
2513:
2493:
2473:
2453:
2432:
2412:
2400:
2398:
2396:
2392:
2387:
2385:
2377:
2374:
2373:
2368:
2366:
2360:
2359:
2354:
2352:
2347:
2341:
2340:
2335:
2330:
2325:
2321:
2316:
2315:
2310:
2306:
2301:
2300:
2297:
2293:
2289:
2283:
2266:
2263:
2260:
2254:
2251:
2243:
2239:
2234:
2230:
2226:
2219:
2215:
2211:
2206:
2202:
2195:
2191:
2187:
2181:
2180:
2175:
2170:
2165:
2161:
2156:
2155:
2150:
2146:
2141:
2140:
2137:
2133:
2129:
2123:
2121:
2102:
2099:
2096:
2090:
2087:
2078:
2076:
2068:
2066:
2052:
2032:
2012:
1991:
1988:
1985:
1965:
1945:
1925:
1919:
1899:
1890:
1876:
1869:to it. Thus,
1856:
1836:
1816:
1810:
1790:
1770:
1750:
1730:
1710:
1687:
1681:
1678:
1675:
1669:
1663:
1657:
1651:
1648:
1641:
1640:
1639:
1625:
1605:
1585:
1565:
1545:
1536:
1517:
1492:
1472:
1460:
1458:
1444:
1422:
1418:
1414:
1409:
1405:
1395:
1379:
1375:
1352:
1348:
1325:
1321:
1298:
1294:
1271:
1267:
1244:
1240:
1217:
1213:
1209:
1204:
1200:
1172:
1168:
1159:
1149:
1145:
1130:
1114:
1110:
1087:
1083:
1062:
1040:
1036:
1013:
1009:
988:
968:
965:
960:
956:
952:
947:
943:
922:
919:
914:
910:
906:
901:
897:
874:
870:
866:
861:
857:
853:
850:
828:
824:
820:
815:
811:
807:
804:
781:
778:
775:
763:
761:
744:
736:
727:
710:
702:
693:
677:
652:
638:
624:
621:
615:
612:
609:
586:
566:
543:
523:
503:
500:
497:
477:
474:
471:
451:
431:
411:
404:derived from
390:
382:
374:
369:
355:
335:
315:
295:
292:
289:
266:
263:
260:
254:
251:
227:
219:
195:
192:
189:
177:
170:
165:
163:
156:
153:
152:
150:
146:
142:
132:
130:
128:
124:
120:
114:
112:
108:
104:
100:
92:
90:
88:
84:
83:Jenő Egerváry
80:
76:
72:
68:
64:
60:
56:
52:
43:
37:
33:
32:Kőnig's lemma
19:
3884:
3858:
3816:
3788:
3782:
3769:
3765:
3762:Kőnig, Dénes
3752:
3748:
3745:Kőnig, Dénes
3703:
3699:
3674:
3668:
3644:
3635:Bondy, J. A.
3615:
3591:
3567:
3515:This is the
3511:
3498:
3486:
3474:
3462:
3441:
3425:
3413:
3400:
3388:
3361:
3349:
3318:
3306:
3302:
3297:
3269:
3265:
3261:
3260:weight of a
3257:
3255:
3254:
3248:
3244:
3237:
3233:
3227:
3226:
3222:
3215:
3209:
3208:
3204:
3197:
3193:
3191:
3182:
3175:
3174:
3170:
3165:
3161:
3160:__________
3159:
3153:
3150:
3146:
3144:
3140:
3137:
3133:
3129:
3127:
3120:
3119:
3117:
3107:
3105:
3102:
3097:
3093:
3092:__________
3091:
3085:
3082:
3078:
3076:
3072:
3069:
3065:
3064:
3062:
3055:
3054:
3053:The maximum
3052:
3045:
3041:
3039:
3038:
3025:
3021:
3018:vertex-cover
3015:
3014:
3010:
3007:
3003:
2996:
2992:
2987:
2972:
2962:
2958:
2954:
2950:
2946:
2942:
2940:
2934:
2930:
2926:
2922:
2918:
2914:
2910:
2906:
2902:
2898:
2894:
2890:
2884:
2875:
2871:
2867:
2863:
2859:
2855:
2851:
2847:
2843:
2839:
2835:
2831:
2827:
2823:
2819:
2816:
2797:
2784:maximum flow
2773:
2749:
2740:
2718:
2706:
2695:
2404:
2388:
2381:
2371:
2370:
2362:
2357:
2356:
2345:
2343:
2333:
2332:
2328:
2323:
2319:
2318:__________
2317:
2311:
2308:
2304:
2302:
2298:
2295:
2291:
2287:
2285:
2241:
2232:
2228:
2224:
2217:
2213:
2207:
2204:
2200:
2193:
2189:
2185:
2183:
2173:
2171:
2168:
2163:
2159:
2158:__________
2157:
2151:
2148:
2144:
2142:
2138:
2135:
2131:
2127:
2125:
2079:
2072:
1891:
1702:
1537:
1464:
1396:
1131:
889:, such that
764:
692:maximum flow
639:
516:to the sink
373:flow network
370:
243:
179:Minimum cut
160:
138:
137:
115:
110:
102:
99:vertex cover
96:
61:, proved by
58:
55:graph theory
51:mathematical
48:
3236:is at most
2887:line graphs
2756:Gyula Kőnig
2743:. However,
2721:Dénes Kőnig
2702:NP-complete
2227:| ones and
1703:Every edge
726:minimum cut
3906:Categories
3559:References
3031:vertices.
1783:. For, if
3772:: 116–119
3755:: 104–119
3713:1205.4605
3301:Called a
3230:-matching
2587:∩
2537:∖
2378:Algorithm
1989:∩
1923:∖
1814:∖
1679:∩
1670:∪
1661:∖
1415:∪
1210:∪
966:⊂
920:⊂
867:∪
821:∪
741:∞
707:∞
640:The size
622:∈
547:∞
501:∈
475:∈
387:∞
224:∞
3857:(1986),
3738:13513566
3641:(1976),
3613:(2011),
3303:covering
3278:See also
3221:for all
3033:Egerváry
2982:Egerváry
2025:. Thus,
1028:or from
745:′
711:′
599:for any
391:′
228:′
107:matching
53:area of
3877:0859549
3843:0406862
3805:0302480
3730:3280546
3691:0124238
3212:-weight
2953:, when
2800:perfect
2725:regular
2715:History
2401:Example
2236:is the
157:Example
139:In any
111:maximum
103:minimum
93:Setting
65: (
49:In the
3891:
3875:
3865:
3841:
3831:
3803:
3736:
3728:
3689:
3653:
3623:
3575:
3305:and a
3207:. The
3006:. The
2921:. If
2812:clique
2806:, the
2764:umlaut
2344:where
2184:where
1397:Thus,
166:Proofs
3734:S2CID
3708:arXiv
3596:(PDF)
3290:Notes
2874:with
2862:with
2850:with
2842:with
559:from
3889:ISBN
3863:ISBN
3829:ISBN
3651:ISBN
3621:ISBN
3573:ISBN
2778:and
1367:and
1313:and
1259:and
935:and
843:and
765:Let
67:1931
3821:doi
3793:doi
3718:doi
3679:doi
3519:of
3432:,
3173:≥
3106:≤
2331:≥
2240:of
2172:≤
2005:in
1723:in
1102:to
1055:to
1001:to
694:in
579:to
77:in
3908::
3873:MR
3871:,
3853:;
3839:MR
3837:,
3827:,
3801:MR
3799:,
3787:,
3770:38
3768:,
3753:34
3751:,
3732:,
3726:MR
3724:,
3716:,
3704:27
3702:,
3687:MR
3685:,
3673:,
3637:;
3609:;
3542:^
3527:^
3373:^
3330:^
3270:w-
3258:w-
3251::
3169:·
3149:≥
3121:w-
3101:·
3081:≥
3056:w-
3046:w-
3042:w-
3016:w-
3008:w-
2977:.
2882:.
2866:-|
2854:-|
2790:.
2766:.
2704:.
2688:.
2673:13
2667:11
2661:10
2611:13
2605:11
2599:10
2576:,
2327:·
2307:≥
2242:G,
2167:·
2147:≥
1457:.
1394:.
762:.
637:.
368:.
97:A
89:.
57:,
3898:.
3846:.
3823::
3808:.
3795::
3789:2
3774:.
3757:.
3720::
3710::
3694:.
3681::
3675:9
3660:.
3630:.
3582:.
3537:.
3506:.
3493:.
3469:.
3457:.
3436:.
3420:.
3356:.
3344:.
3266:b
3262:b
3249:b
3245:w
3240:v
3238:b
3234:v
3228:b
3223:v
3218:v
3216:b
3210:b
3205:b
3200:v
3198:b
3194:v
3178:.
3176:w
3171:y
3166:G
3162:A
3155:V
3151:0
3147:y
3141:y
3138:·
3134:V
3130:1
3113:.
3111:V
3108:1
3103:x
3098:G
3094:A
3087:E
3083:0
3079:x
3073:x
3070:·
3066:w
3028:e
3026:w
3022:e
3004:w
2999:e
2997:w
2993:e
2963:G
2959:G
2955:G
2951:G
2947:G
2943:G
2935:G
2931:G
2929:(
2927:L
2923:G
2919:G
2915:G
2913:(
2911:L
2907:G
2903:G
2899:G
2897:(
2895:L
2891:G
2876:M
2872:G
2868:M
2864:n
2860:G
2856:M
2852:n
2848:G
2844:n
2840:G
2836:M
2832:G
2828:G
2824:G
2820:G
2676:}
2670:,
2664:,
2658:,
2655:6
2652:,
2649:4
2646:,
2643:2
2640:{
2637:=
2634:K
2614:}
2608:,
2602:,
2596:{
2593:=
2590:Z
2584:R
2564:}
2561:6
2558:,
2555:4
2552:,
2549:2
2546:{
2543:=
2540:Z
2534:L
2514:Z
2494:U
2474:L
2454:U
2433:R
2413:L
2346:y
2339:.
2337:E
2334:1
2329:y
2324:G
2320:A
2313:V
2309:0
2305:y
2299:y
2296:·
2292:V
2288:1
2270:)
2267:E
2264:,
2261:V
2258:(
2255:=
2252:G
2233:G
2229:A
2225:V
2221:V
2218:1
2214:E
2209:E
2205:0
2201:E
2197:E
2194:1
2190:E
2186:x
2179:.
2177:V
2174:1
2169:x
2164:G
2160:A
2153:E
2149:0
2145:x
2139:x
2136:·
2132:E
2128:1
2122::
2106:)
2103:E
2100:,
2097:V
2094:(
2091:=
2088:G
2053:M
2033:K
2013:K
1992:Z
1986:B
1966:U
1946:Z
1926:Z
1920:A
1900:K
1877:K
1857:e
1837:e
1817:Z
1811:A
1791:e
1771:K
1751:K
1731:E
1711:e
1688:.
1685:)
1682:Z
1676:B
1673:(
1667:)
1664:Z
1658:A
1655:(
1652:=
1649:K
1626:U
1606:U
1586:Z
1566:A
1546:U
1522:|
1518:M
1514:|
1493:M
1473:M
1445:G
1423:S
1419:B
1410:T
1406:A
1380:T
1376:B
1353:S
1349:A
1326:T
1322:B
1299:S
1295:A
1272:S
1268:B
1245:T
1241:A
1218:S
1214:B
1205:T
1201:A
1179:|
1173:S
1169:B
1164:|
1160:+
1156:|
1150:T
1146:A
1141:|
1115:T
1111:B
1088:S
1084:A
1063:t
1041:S
1037:B
1014:T
1010:A
989:s
969:T
961:T
957:B
953:,
948:T
944:A
923:S
915:S
911:B
907:,
902:S
898:A
875:T
871:B
862:S
858:B
854:=
851:B
829:T
825:A
816:S
812:A
808:=
805:A
785:)
782:T
779:,
776:S
773:(
737:G
703:G
678:G
657:|
653:M
649:|
625:E
619:)
616:b
613:,
610:a
607:(
587:b
567:a
544:+
524:t
504:B
498:b
478:A
472:a
452:s
432:1
412:G
383:G
356:G
336:M
316:V
296:B
293:,
290:A
270:)
267:E
264:,
261:V
258:(
255:=
252:G
220:G
199:)
196:T
193:,
190:S
187:(
151:.
38:.
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.