253:
22:
47:
159:
of a given graph is another graph formed by deleting vertices, deleting edges, and contracting edges. When an edge is contracted, its two endpoints are merged to form a single vertex. In some versions of graph minor theory the graph resulting from a contraction is simplified by removing self-loops
181:
If a given graph is planar, so are all its minors: vertex and edge deletion obviously preserve planarity, and edge contraction can also be done in a planarity-preserving way, by leaving one of the two endpoints of the contracted edge in place and routing all of the edges that were incident to the
398:(a generalization of the forbidden minor characterization of planar graphs, stating that every graph family closed under the operation of taking minors has a characterization by a finite number of forbidden minors). Analogues of Wagner's theorem can also be extended to the theory of
186:
non-planar graph is a graph that is not planar, but in which all proper minors (minors formed by at least one deletion or contraction) are planar. Another way of stating Wagner's theorem is that there are only two minor-minimal non-planar graphs,
164:
are allowed, but this variation makes no difference to Wagner's theorem. Wagner's theorem states that every graph has either a planar embedding, or a minor of one of two types, the complete graph
336:, it is straightforward to prove that a graph that has at least one of these two graphs as a minor also has at least one of them as a subdivision, so the two theorems are equivalent.
318:. In a sense, Kuratowski's theorem is stronger than Wagner's theorem: a subdivision can be converted into a minor of the same type by contracting all but one edge in each
322:
formed by the subdivision process, but converting a minor into a subdivision of the same type is not always possible. However, in the case of the two graphs
351:
minor. The theorem can be rephrased as stating that every such graph is either planar or it can be decomposed into simpler pieces. Using this idea, the
383:
Wagner's theorem is an important precursor to the theory of graph minors, which culminated in the proofs of two deep and far-reaching results: the
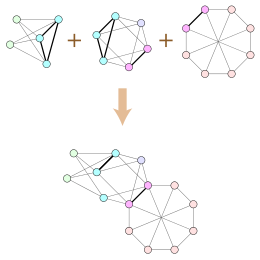
42:(small colored circles and solid black edges). The minors may be formed by deleting the red vertex and contracting edges within each yellow circle.
344:
One consequence of the stronger version of Wagner's theorem for four-connected graphs is to characterize the graphs that do not have a
688:
648:
608:
534:
70:
358:-minor-free graphs may be characterized as the graphs that can be formed as combinations of planar graphs and the eight-vertex
230:
395:
120:
624:
136:
683:
594:
373:
can be formed in this way as a clique-sum of three planar graphs, each of which is a copy of the tetrahedral graph
301:
155:, in such a way that the only intersections between pairs of edges are at a common endpoint of the two edges. A
290:
205:
112:
384:
297:
268:
252:
678:
550:
148:
97:
479:
319:
256:
152:
461:
644:
604:
598:
530:
524:
516:
241:
636:
562:
498:
453:
658:
576:
654:
572:
417:
300:, according to which a graph is planar if and only if it does not contain as a subgraph a
260:
144:
132:
222:
can be made unnecessary in the characterization, leaving only a single forbidden minor,
590:
520:
483:
93:
39:
21:
640:
416:(along with three other forbidden configurations) appear in a characterization of the
672:
465:
421:
140:
108:
441:
359:
264:
78:
74:
62:
567:
156:
116:
82:
363:
296:
Wagner published both theorems in 1937, subsequent to the 1930 publication of
161:
502:
233:
states that a 5-connected graph is planar if and only if it does not have
178:. (It is also possible for a single graph to have both types of minor.)
115:
on six vertices). This was one of the earliest results in the theory of
529:, Graduate Texts in Mathematics, vol. 244, Springer, p. 269,
457:
399:
46:
215:
minor. That is, by assuming a higher level of connectivity, the graph
204:
Another result also sometimes known as Wagner's theorem states that a
251:
50:
A clique-sum of two planar graphs and the Wagner graph, forming a
45:
20:
627:(1980), "On Tutte's characterization of graphic matroids",
81:, stating that a finite graph is planar if and only if its
387:(a generalization of Wagner's clique-sum decomposition of
182:
other endpoint along the path of the contracted edge. A
444:(1937), "Über eine Eigenschaft der ebenen Komplexe",
484:"Sur le problème des courbes gauches en topologie"
160:and multiple adjacencies, while in other version
555:Bulletin of the American Mathematical Society
8:
248:History and relation to Kuratowski's theorem
566:
208:graph is planar if and only if it has no
603:(5th ed.), CRC Press, p. 307,
304:of one of the same two forbidden graphs
433:
119:and can be seen as a forerunner of the
402:: in particular, the same two graphs
7:
16:On forbidden minors in planar graphs
38:(right) as minors of the nonplanar
14:
171:or the complete bipartite graph
71:forbidden graph characterization
629:Annals of Discrete Mathematics
553:(2006), "Graph minor theory",
1:
641:10.1016/S0167-5060(08)70855-0
568:10.1090/S0273-0979-05-01088-8
394:-minor-free graphs) and the
705:
366:operations. For instance,
231:Kelmans–Seymour conjecture
396:Robertson–Seymour theorem
127:Definitions and statement
121:Robertson–Seymour theorem
689:Theorems in graph theory
113:complete bipartite graph
503:10.4064/fm-15-1-271-283
385:graph structure theorem
247:
229:. Correspondingly, the
293:
147:, with points for its
58:
43:
600:Graphs & Digraphs
480:Kuratowski, Kazimierz
255:
49:
24:
362:, glued together by
298:Kuratowski's theorem
143:of the graph in the
275:and finding either
257:Proof without words
151:and curves for its
684:Graph minor theory
593:; Lesniak, Linda;
458:10.1007/BF01594196
294:
69:is a mathematical
59:
44:
273:Wagner's theorems
242:topological minor
696:
663:
661:
621:
615:
613:
587:
581:
579:
570:
547:
541:
539:
513:
507:
505:
488:
476:
470:
468:
438:
418:graphic matroids
85:include neither
67:Wagner's theorem
704:
703:
699:
698:
697:
695:
694:
693:
669:
668:
667:
666:
651:
623:
622:
618:
611:
591:Chartrand, Gary
589:
588:
584:
549:
548:
544:
537:
515:
514:
510:
486:
478:
477:
473:
440:
439:
435:
430:
415:
408:
393:
379:
372:
357:
350:
342:
335:
328:
317:
310:
288:
281:
261:hypercube graph
250:
239:
228:
221:
214:
200:
193:
177:
170:
145:Euclidean plane
129:
106:
91:
56:
37:
30:
17:
12:
11:
5:
702:
700:
692:
691:
686:
681:
671:
670:
665:
664:
649:
625:Seymour, P. D.
616:
609:
582:
551:Lovász, László
542:
535:
508:
471:
432:
431:
429:
426:
422:matroid minors
413:
406:
391:
377:
370:
355:
348:
341:
338:
333:
326:
315:
308:
286:
279:
249:
246:
237:
226:
219:
212:
206:four-connected
198:
191:
175:
168:
128:
125:
104:
94:complete graph
89:
77:, named after
54:
40:Petersen graph
35:
28:
15:
13:
10:
9:
6:
4:
3:
2:
701:
690:
687:
685:
682:
680:
679:Planar graphs
677:
676:
674:
660:
656:
652:
650:9780444861108
646:
642:
638:
634:
630:
626:
620:
617:
612:
610:9781439826270
606:
602:
601:
596:
592:
586:
583:
578:
574:
569:
564:
560:
556:
552:
546:
543:
538:
536:9781846289699
532:
528:
527:
522:
521:Murty, U.S.R.
518:
512:
509:
504:
500:
496:
493:(in French),
492:
485:
481:
475:
472:
467:
463:
459:
455:
451:
447:
443:
437:
434:
427:
425:
423:
420:by forbidden
419:
412:
405:
401:
397:
390:
386:
381:
376:
369:
365:
361:
354:
347:
339:
337:
332:
325:
321:
314:
307:
303:
299:
292:
285:
278:
274:
270:
266:
262:
258:
254:
245:
243:
236:
232:
225:
218:
211:
207:
202:
197:
190:
185:
184:minor-minimal
179:
174:
167:
163:
158:
154:
150:
146:
142:
138:
134:
126:
124:
122:
118:
114:
110:
109:utility graph
103:
99:
95:
88:
84:
80:
76:
75:planar graphs
72:
68:
64:
53:
48:
41:
34:
27:
23:
19:
632:
628:
619:
599:
585:
561:(1): 75–86,
558:
554:
545:
526:Graph Theory
525:
517:Bondy, J. A.
511:
494:
490:
474:
449:
445:
436:
410:
403:
388:
382:
374:
367:
360:Wagner graph
352:
345:
343:
340:Implications
330:
323:
312:
305:
295:
283:
276:
272:
269:Kuratowski's
234:
223:
216:
209:
203:
195:
188:
183:
180:
172:
165:
130:
117:graph minors
101:
86:
79:Klaus Wagner
66:
63:graph theory
60:
57:-free graph.
51:
32:
25:
18:
595:Zhang, Ping
497:: 271–283,
491:Fund. Math.
452:: 570–590,
302:subdivision
162:multigraphs
135:of a given
31:(left) and
673:Categories
446:Math. Ann.
442:Wagner, K.
428:References
364:clique-sum
265:non-planar
635:: 83–90,
466:123534907
291:subgraphs
289:(bottom)
282:(top) or
133:embedding
131:A planar
597:(2010),
523:(2008),
482:(1930),
400:matroids
149:vertices
98:vertices
96:on five
659:0597159
577:2188176
259:that a
141:drawing
657:
647:
607:
575:
533:
464:
267:using
100:) nor
83:minors
487:(PDF)
462:S2CID
240:as a
157:minor
153:edges
139:is a
137:graph
107:(the
92:(the
645:ISBN
605:ISBN
531:ISBN
409:and
329:and
320:path
311:and
194:and
111:, a
637:doi
563:doi
499:doi
454:doi
450:114
414:3,3
371:3,3
334:3,3
316:3,3
287:3,3
271:or
263:is
220:3,3
199:3,3
176:3,3
105:3,3
73:of
61:In
36:3,3
675::
655:MR
653:,
643:,
631:,
573:MR
571:,
559:43
557:,
519:;
495:15
489:,
460:,
448:,
424:.
380:.
244:.
201:.
123:.
65:,
662:.
639::
633:8
614:.
580:.
565::
540:.
506:.
501::
469:.
456::
411:K
407:5
404:K
392:5
389:K
378:4
375:K
368:K
356:5
353:K
349:5
346:K
331:K
327:5
324:K
313:K
309:5
306:K
284:K
280:5
277:K
238:5
235:K
227:5
224:K
217:K
213:5
210:K
196:K
192:5
189:K
173:K
169:5
166:K
102:K
90:5
87:K
55:5
52:K
33:K
29:5
26:K
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.