Knowledge

The IEC standard and most current literature treat noise-figure ${\displaystyle (NF)}$ as the dB representation of noise-factor ${\displaystyle (F)}$—i.e. for ${\displaystyle F=20{\text{,}}}$ ${\displaystyle NF=13\ {\text{dB.}}}$ Alternatively, the IEEE standard and some literature and treat ${\displaystyle NF}$ and ${\displaystyle F}$ as synonymous and linear. ${\displaystyle F}$ is defined in two different noninterchangeable ways. For case-1, ${\displaystyle F}$ the ratio of the input to output SNR of a 2-port device—i.e. ${\displaystyle F=SNR_{in}/SNR_{out}{\text{,}}}$ so ${\displaystyle F=20}$ means the SNR between an input and output port has dropped by a factor of ${\displaystyle 20}$ ${\displaystyle {\text{or }}(13\ {\text{dB}})}$. Lower numbers are always better since they indicate less SNR degradation. For case-2, ${\displaystyle F}$ is a non-linear transformation of an effective noise temperature ${\displaystyle T_{e}}$ at a port on a device—i.e. ${\displaystyle F=1+T_{e}/290\ {\text{K}}{\text{.}}}$ Thus ${\displaystyle F=20}$ means the noise temperature at that port is ${\displaystyle 5510\ {\text{K}}{\text{.}}}$ When ${\displaystyle T_{e}}$ applies to the input of a 2-port device, ${\displaystyle F}$ non-linearly expresses an absolute input sensitivity, not an SNR degradation. Lower values are better. When ${\displaystyle T_{e}}$ applies to an output port, ${\displaystyle F}$ non-linearly expresses an absolute output noise power and as such, whether or not higher or lower values are better depends on the application.

There are two entirely different non-interchangeable definitions and meanings for noise-figure in common use. The first (case-1) noise figure definition originated from Friis in 1944. It is a function of two arguments and means an SNR loss between two ports. — The second (case-2) originated from the Institute of Electrical and Electronics Engineers (IEEE) in 1959. It is a function of a single argument and does not mean an SNR loss but is instead a non-linear proxy or mapping for a noise temperature at a port. Not only in literature but even in some calculators, noise-figure values and meanings get wrongly intertwined and misused. The goal of this article is to for you to fully understand and distinguish between each definition. It is meant to enable you to identify which “noise-figure” is operative in texts you are reading so your understanding is precise and consistent with the definition being used in the term’s contextual usage. It is meant to prevent you from falling victim to errors caused by misunderstanding and intertwining the two-definitions.

The nomenclature of reference keeps the definitions distinct by using the subscript "op", as in ${\displaystyle F_{op}}$, for Friis's definition, and using the subscript "0", as in ${\displaystyle F_{0}}$, for the IEEE standard's definition. This article adopts the same "op" subscript for Friis's SNR based definition, where ${\displaystyle F_{op}}$ and ${\displaystyle NF_{op}}$ indicate noise-factor and noise-figure respectively. "Op" was chosen to represent "operating" since the Friis noise figure is based on the in-situ "operating" noise temperature of the source. More in keeping with the nomenclature of reference , this article uses the subscript "std" (for IEEE/IEC standard temperature), to identify terms using the IEEE standard's, and the International Electrotechnical Commission (IEC) standard's, definitions. "Std" was chosen to indicate the definition is based on a standard-temperature based definition, not the actual operating source noise temperature. So we have ${\displaystyle F_{std}}$ and ${\displaystyle NF_{std}}$ indicate noise-factor and noise-figure respectively.

The linear versus dB nomenclature commonly used in current industry application-notes, books, magazines, journals and specified by the IEC is that ${\displaystyle F}$ (noise-factor) is a linear (or arithmetic) power ratio, and ${\displaystyle NF}$ (noise-figure) is the decibel (dB) representation of ${\displaystyle F}$. Nonetheless, there are many books and articles and online calculators where the terms ${\displaystyle F}$ and ${\displaystyle NF}$ are synonyms and both linear, as they are in the IEEE and Federal standards. To be formally accurate to these two standards, we would need an ${\displaystyle NF_{IEEE{\text{ }}std}}$ that was linear (and thus equal to ${\displaystyle F_{std}}$), and an ${\displaystyle NF_{IEC{\text{ }}std}}$ that was dB. We will not do that. This article will use the more common ${\displaystyle F}$=linear and ${\displaystyle NF}$=dB nomenclature for both "op" and "std" definitions. Since ${\displaystyle F}$ is a linear power ratio (not a voltage ratio), the conversion to dB is 10 log (not 20 log), so,

${\displaystyle {\text{Noise Figure}}=NF=10{\text{ }}{\log }_{10}\left(F\right){\text{ and}}}$

(1)

${\displaystyle {\text{Noise Factor}}=F=10^{\frac {NF}{10}}{\text{.}}}$

(2)

As a result of the mixed dB vs. linear nomenclature and multiple meanings associated with "noise figure", it is vital that a reader of literature using the term, or a user of a calculator using the term, not only determine which definition ("op" vs "std") is operational (i.e. by the context of its use), but also determine if/when the term refers to a linear or dB value. Readers and authors must carefully use each definition consistently with what it means since the meanings and numbers connected to each term are not interchangeable.

A few terms need to be introduced in order to give meaning to the definitional equations for noise-figure. This article will use the term "block" or "device" to mean an object that has a noise figure, such as a component like a transistor amplifier or antenna, or an entire signal chain composed of a sequence of many components, like a dual Superheterodyne receiver. Underlying technical terms include: (1) the effective noise bandwidth ${\displaystyle (B)}$ of a block, (2) signal-to-noise ratio (SNR), (3) the effective noise temperature of a source ${\displaystyle (T_{s})}$ (“s” for source) that drives a block’s input, and (4) the effective noise temperature ${\displaystyle (T_{e})}$ (“e” for effective) at a port, which is typically understood to be a block's input port for 2-port networks unless otherwise stated. These terms are formally defined in the § Definitions Of Underlying Terms section.

Literature sometimes uses the term ${\displaystyle T_{0}}$ as a variable representing an actual arbitrary operating source noise temperature ${\displaystyle T_{s}}$. Literature also uses ${\displaystyle T_{0}}$ as a fixed, non-variable "standard temperature", typically being the IEEE/IEC standard's ${\displaystyle 290\ {\text{K}}.}$ Some literature even uses ${\displaystyle T_{0}}$ to represent both—i.e. a variable representing the operational ${\displaystyle T_{s}}$ in one equation and representing a fixed ${\displaystyle 290\ {\text{K}}}$ in another equation. This dual usage can lead to serious confusion regarding what ${\displaystyle T_{0}}$ means in any particular equation and how to properly apply the equation as well as serious errors in derivative formulas. It is vital that readers of noise figure literature carefully track the usage of such noise temperature terms to ensure that the two noise-figure meanings are kept distinct. In this article the term ${\displaystyle T_{s}}$ is always a variable that represents an arbitrary in-situ operational source temperature, and the number ${\displaystyle 290\ {\text{K}}}$ is always used to represent the "standard temperature"—the temperature specified by the IEEE standard and essentially specified by the IEC standard which says "around ${\displaystyle 290\ {\text{K}}}$".

In frequency translating components or heterodyne systems, such as the noise figure applied to a mixer, the input noise power ${\displaystyle n_{in}}$ is assumed to only cover the desired frequencies—not image or spurious frequencies. Here, "image frequencies" include the local oscillator (LO) image sideband (i.e. an undesired upper or lower sideband). "Spurious" includes frequency bands that fall on on top of the desired frequencies due to mix terms from harmonics of the LO and inter modulation products. As such, the component of the output noise ${\displaystyle n_{out}}$ that comes from ${\displaystyle n_{in}}$ only comes via the principal frequency transformation of the system. The IEEE and IEC standards exclude noise appearing via any image frequency transformations. In practice, ${\displaystyle n_{in}}$ is not necessarily band limited (I.e. ${\displaystyle n_{in}}$ does cover image and spurious frequencies). In this case, a frequency translating device's impact on the SNR will be higher since the noise power from the noise in the image bands will be added to the output noise.

A 2-port's noise figure is only meaningful when it is accompanied by the source's impedance since a 2-port device's input ${\displaystyle T_{e}}$ is a function of the impedance of the source driving it. The lowest noise figure on typical 2-port active devices occurs when the source impedance is not matched to the input impedance of the device (i.e. they are not complex conjugates of each other). Feedback circuits can be used to simultaneously minimize noise figure and achieve an input impedance match.

The derivations and equations in this article assume matched conditions unless specified otherwise, such as in the § Antenna Noise Figure section.

Friis's definition is: ${\displaystyle F_{op}}$ is the ratio of (1) the output noise power of a device to (2) the portion thereof attributable to thermal noise in the input termination. ${\displaystyle NF_{op}}$ and ${\displaystyle F_{op}}$ are measures of the degradation in the signal-to-noise ratio between two ports—an input port and an output port. ${\displaystyle F_{op}}$ is the ratio of input SNR to output SNR.

${\displaystyle F_{op}={\frac {{SNR}_{in}}{{SNR}_{out}}}}$

(3)

${\displaystyle F_{op}}$ cannot be less than ${\displaystyle 1}$ (i.e. ${\displaystyle F_{op}\geq 1}$). ${\displaystyle NF_{op}}$ is the number of dB that the SNR has dropped by.

${\displaystyle {NF}_{op}={SNR}_{{in}_{dB}}-{SNR}_{{out}_{dB}}}$

(4)

${\displaystyle NF_{op}}$ cannot go negative (i.e. ${\displaystyle NF_{op}\geq 0}$). ${\displaystyle F_{op}}$ only applies to 2-port devices—it requires an input and output. Under this definition two noise temperatures are required to compute ${\displaystyle F_{op}{\text{,}}}$ (a) the effective input noise temperature of the device, ${\displaystyle T_{e}{\text{,}}}$ and (b) the noise temperature of the source driving the input of the device, ${\displaystyle T_{s}}$. Assuming the impedance the source and the device's input match ${\displaystyle ({\text{ i.e. }}Z_{source}^{*}=Z_{in}){\text{,}}}$ so there is no reflection, and assuming ${\displaystyle T_{e}}$ was measured when sourced with this impedance, ${\displaystyle F_{op}}$ is the two parameter function,

${\displaystyle F_{op}=f(T_{e},T_{s})=1+{\frac {T_{e}}{T_{s}}}{\text{,}}}$

(5)

with inverses of

${\displaystyle T_{e}=\left(F_{op}-1\right)T_{s}{\text{, and }}}$

(6)

${\displaystyle T_{s}={\frac {T_{e}}{F_{op}-1}}{\text{.}}}$

(7)

The derivations of the above formulas are shown in the section, § History and Derivation of First Definition (Friis).

Friis's ${\displaystyle NF_{op}}$ answers the question, “If I connect a particular block to a source (like an antenna, or sensor or the output of a previous amplifier) that is putting out noise in addition to the signal, how much worse (lower in dB) will the block’s output SNR be relative to that of a block that is identical but perfectly noiseless?" Or in other words, "how much worse is the output SNR relative to the input SNR--where the input SNR is based on the operating input noise, measured in the same noise bandwidth as that of the block?" Under Friis's definition, “noise-figure” is an operational system-specific metric. In other words, the ${\displaystyle NF_{op}}$ of a block depends on the noise level coming into it. The block's ${\displaystyle NF_{op}}$ cannot be determined apart from knowing the noise level feeding into it from the system to which it is attached. ${\displaystyle {NF}_{op}}$ characterizes how much a block, as used in the system it is connected to, degrades the signal-to-noise ratio.

What ${\displaystyle F_{op}}$ is:

(1) A precise SNR reduction metric — The SNR reduction between an input port and an output port. Lower numbers are always better and indicate a sensitivity closer to the optimum.

(2) An in-situ metric — it depends on the noise coming into the 2-port device.

(3) A function of two parameters, as shown in equation 5, (a) the in-situ source temperature (the temperature driving the input of the device) and (b) the effective input noise temperature of the device when its input is terminated with the impedance of the source.

(4) A function that only applies to devices with two ports—devices must have an input and an output.

What it is not:

(1) It is not the "noise figure" you find on the data sheet of an isolated component like an amplifier, receiver, antenna, or noise source.

(2) It is not a measure of absolute sensitivity.

Formally, the IEEE's definition is

${\displaystyle {F}_{std}=1+\left.{\frac {{T}_{e}}{290^{\circ }{K}}}\right|_{{T}_{s}=290\ {\text{K}}}}$

(8)

While formally, the definition requires the above constrained formula and requires a 2-port network and a known and exact source temperature, in practice, the IEEE's definition is treated as an unconstrained single-parameter function that applies to a port on a device, or in other words, any 1-port on an n-port device. As a result, in practice, it is not the same as the Friis "noise figure" ${\displaystyle NF_{op}{\text{.}}}$ Mathematically, as practiced,

${\displaystyle F_{std}=h(T_{e})=1+{T_{e}}/290\ {\text{K}}{\text{,}}}$

(9)

with an inverse of,

${\displaystyle T_{e}=(F_{std}-1)290\ {\text{K}}{\text{ }}}$

(10)

where ${\displaystyle T_{e}}$ is either (1) the effective input noise temperature of a 2-port device, or (2) the effective output noise temperature of the noise coming out of the port being characterized. Using this "as practiced" definition, ${\displaystyle F_{std}}$ is simply a nonlinear monotonic function of a noise power associated with a port (any port). These equations (a) do not account for the actual "in-situ" source temperature and (b) do not require two ports, both of which are required to compute an ${\displaystyle F_{op}}$. The derivation of these formulas from the formal IEEE standard is shown in the section, § History and Derivation of Second Definition (IEEE).

${\displaystyle F_{std}}$, as defined in equation 9, is not an SNR reduction measure. It is important, therefore, that ${\displaystyle F_{std}}$ never be understood to mean, or used in a way where it is implied to mean, an SNR reduction—including never being treated or thought of as if it was an approximation to an SNR reduction.Moreover, equation 9 cannot be used in derivations that rely on ${\displaystyle F_{std}}$ being an SNR reduction metric, because it is not. Instead, the formula is simply a non-linear monotonic function of one argument, a noise temperature at a port. When given an IEEE or IEC ${\displaystyle NF_{std}}$ number, the one and only thing it always represents, and can always be converted back to, is a noise temperature. Properly understanding that the common use of an IEEE/IEC "noise-figure" number is that simple―it non-linearly represents a noise temperature. Never treat it or think of it as a Friis noise-figure (SNR reduction metric), but instead, always think of it and use it as a proxy for an effective noise temperature at a port.

Functions with different argument lists are, in general, not equal. And this non-equality is also the case between equations 5 and 9 and the equations that follow from them. In other words,

${\displaystyle h\left(T_{e}\right)\neq f\left(T_{e},T_{s}\right){\text{, so}}}$

(11)

${\displaystyle {NF}_{std}\neq {SNR}_{{in}_{dB}}-{SNR}_{{out}_{dB}}{\text{, and}}}$

(12)

${\displaystyle F_{std}\neq {\frac {{SNR}_{in}}{{SNR}_{out}}}{\text{.}}}$

(13)

For example, an outcome of equation 12 is that in general, replacing an 11 dB ${\displaystyle NF_{std}}$ amplifier with a 1 dB ${\displaystyle NF_{std}}$ amplifier does not improve the SNR by 10 dB. Due to widespread confusion over the above inequalities, class notes from Jim Stiles from the University of Kansas, where he is referring to the IEEE/IEC noise factor ${\displaystyle F{\text{,}}}$ justifiably emphasizes,

“It is critically important that you understand the definition of noise figure. A common mistake is to assume that ${\displaystyle SNR_{out}={\frac {SNR_{in}}{F}}\longleftarrow }$ This is not generally true!”

He is emphasizing for his students the fact that the ${\displaystyle F}$ defined by the IEEE and IEC standards cannot be interchanged with the ${\displaystyle F}$ defined by Friis. In other words, he is emphasizing that ${\displaystyle F_{std}\neq F_{op}{\text{.}}}$

What ${\displaystyle F_{std}}$ is, as practiced:

(1) It is the "noise figure" you find on the data sheet of an isolated component, like an amplifier, receiver, noise source, or sensor.

(2) It is a nonlinear monotonic function of (or a proxy for) the noise temperature of a port.

(3) It pertains to an isolated (not in-situ) device, (except for antennas, see § Antenna Noise Figure)

(4) It is a function of 1 parameter, the noise temperature of a port.

(5) It is a proxy for a 2-port device's absolute sensitivity when it represents the effective input noise temperature of that 2-port device. In this particular 2-port case, lower numbers are always better, meaning better absolute sensitivity.

What it is not:

(1) It is not a measure of SNR degradation between two ports.

(2) it is not a sensitivity metric when it applies to an output port, where lower numbers may not be better, such as an antenna (see § Antenna Noise Figure)

(3) It is not a function requiring two ports and two parameters.

Since ${\displaystyle NF_{std}}$ is a proxy for an effective noise temperature ${\displaystyle T_{e}}$ at a port, the noise temperature being specified via an ${\displaystyle NF_{std}}$ is equally specified simply by ${\displaystyle T_{e}}$ itself. Applying this fact means that listing a noise temperature ${\displaystyle T_{e}}$ on the specification sheet of an amplifier communicates the exact same information as listing its ${\displaystyle NF_{std}{\text{.}}}$ Because of this fact, readers should be ready to read data sheets with noise specified either way. An example using a noise temperature instead of NF is .

Many users and manufacturers prefer that the noise temperature be specified as opposed to an IEEE/IEC ${\displaystyle NF_{std}}$ because: (1) on the manufacturer's side, since the measurement process always starts with the measurement of a noise temperature in the first place, so specifying the noise temperature on a data sheet eliminates the step of converting from noise temperature to an IEEE/IEC noise figure; (2) on the user's side, having the noise temperature eliminates the step of converting the IEEE/IEC noise figure back to a temperature so it can be used in an SNR analysis; and (3) on both sides, having the noise temperature allows easier "in your head" comparisons since noise power is linearly related to noise temperature. For example, the meaning of doubling the noise temperature is obvious and simply means the noise power has doubled, whereas, an IEEE/IEC noise factor is a unitless non-linear number that requires calculation to figure out what it means and what a change in it means.

A number of procedures and test setups are used to measure noise bandwidths, noise power, effective noise temperatures, the noise parameters of devices, and ultimately a noise figure. These procedures will not be covered in this article. References cover classic techniques. Noise figure measurement remains an active area of investigation, where ongoing goals include more accuracy, or faster measurement, or reduced equipment needs. References represent some of the more recent work, such as using an uncalibrated noise source as opposed to using hot and cold calibrated noise sources.

The noise factor for a general 2-port network is generally modeled with 4 real variables, (1) the minimum noise temperature, the (2) real and (3) imaginary parts of the optimum source impedance (sometimes written as an admittance or reflection coefficient) that produce the minimum effective noise temperature, and (4) a real value ${\displaystyle R_{n}}$ ("noise resistance") that captures how quickly the effective noise temperature rises as the source impedance moves away from the optimum. Methods of using a noise figure model to optimize the noise figure of amplifiers are illustrated in references . Techniques for measuring the noise parameters of an antenna element are described in reference , and for a phased array in reference.

This article is intended to help electronics enthusiasts, engineers, and physicists understand each definition, understand their differences, be able to read literature using the terms and determine which definition is active in any particular equation or usage, and apply each consistently with its unique meaning.

The § Key Associated Formulas section illuminates important limitations and assumptions in commonly published formulas and their dependence on which definition is being used. It includes formulas that rarely appear in the literature. it also includes § Rules for SNR calculations to help practitioners use each metric ("std" and "op") consistently with its definition. The § Example Usage section explains by way of example, the usage and application of both definitions, including what happens when a definition is misapplied. Antennas require special attention which is covered in the § Antenna Noise Figure section. The sections § History and Derivation of First Definition (Friis) and § History and Derivation of Second Definition (IEEE/IEC) provide the underlying derivations that go deeper into details than the above overview. Underlying terms are explained in the § Definitions of Underlying Terms section. And finally, the § References section provides numerous links to related textbooks, refereed journal papers, standards, microwave industry application notes, graduate school class handouts, and web sites.

After digesting the material in this article, a reader should be able to read literature discussing noise-figure and correctly understand and apply both definitions—if the literature is read carefully, with an eye toward keeping separate any mixing of the two definitions and any mixing in the usage of its noise temperature terms.

Cascaded Signal Chain Effective Input Noise Temperature ${\displaystyle {T}_{e}}$

The total effective input noise ${\displaystyle {T}_{e}}$ for a series of cascaded devices, where the n device has an effective input noise temperature of ${\displaystyle {T}_{n}}$ and gain ${\displaystyle {G}_{n}{\text{,}}}$ is easily derived. It is simply the solution to an equation for the noise coming out of a string of amplifiers, where the left side of the equation has a single effective noise temperature for the chain, and the right side has the individual temperatures of each stage in the chain, and the gains on the both sides match. The setup is shown pictorially in the figure to the right. The equation to be solved is,

${\displaystyle {T}_{e}{G}_{1}{G}_{2}{G}_{3}\cdots =\left(\left({T}_{1}{G}_{1}+{T}_{2}\right){G}_{2}+{T}_{3}\right){G}_{3}\cdots }$

The solution to this equation is called the “Friis formula for noise temperature”, and is,

${\displaystyle {T}_{e}={T}_{1}+{\frac {{T}_{2}}{{G}_{1}}}+{\frac {{T}_{3}}{{G}_{1}{G}_{2}}}+{\frac {{T}_{4}}{{G}_{1}{G}_{2}{G}_{3}}}+\cdots +{\frac {{T}_{n}}{{G}_{1}{G}_{2}{G}_{3}\cdots {G}_{n-1}}}{\text{.}}}$

(14)

This formula is completely general and not specific to IEEE/IEC or Friis noise figure definitions. Importantly, there are no hidden assumptions as there are in the formulas for a cascaded signal chain's noise factor. It applies to all blocks and systems. It uses simple well defined terms. And the equation is simple to apply.

Cascaded Signal Chain IEEE/IEC (standard) Effective Noise Factor ${\displaystyle {F}_{e_{std}}}$

Two formulas, one for each definition, are required for finding the overall "effective noise factor" ${\displaystyle {F}_{e}}$ for a series of cascaded devices with gains ${\displaystyle {G}_{n}}$ and noise factors ${\displaystyle {F}_{n}{\text{.}}}$

If the ${\displaystyle F_{n}}$ are all IEEE/IEC ${\displaystyle F_{std}}$ numbers, or if all ${\displaystyle F_{n}}$ and ${\displaystyle {F}_{e_{std}}}$ are based on a common source noise temperature ${\displaystyle {T}_{s}}$, then the formula is ,

${\displaystyle {F}_{e_{std}}={F}_{1}+{\frac {{F}_{2}-1}{{G}_{1}}}+{\frac {{F}_{3}-1}{{G}_{1}{G}_{2}}}+{\frac {{F}_{4}-1}{{G}_{1}{G}_{2}{G}_{3}}}+\cdots +{\frac {{F}_{n}-1}{{G}_{1}{G}_{2}{G}_{3}\cdots {G}_{n-1}}}{\text{.}}}$

(15)

This formula fails when the ${\displaystyle {F}_{n}}$ refer to Friis noise factors.

Cascaded Signal Chain Friis (operational) Effective Noise Factor ${\displaystyle {F}_{e_{op}}}$

If the ${\displaystyle F_{n}}$ are all Friis ${\displaystyle F_{op}}$ numbers then the formula is ,

${\displaystyle {F}_{e_{op}}={F}_{1}+{\frac {{T}_{s(2)}{(F_{2}-1)}}{{T}_{s(1)}{G}_{1}}}+{\frac {{T}_{s(3)}{(F_{3}-1)}}{{T}_{s(1)}{G}_{1}{G}_{2}}}+{\frac {{T}_{s(4)}{(F_{4}-1)}}{{T}_{s(1)}{G}_{1}{G}_{2}{G}_{3}}}+\cdots +{\frac {{T}_{s(n)}{(F_{n}-1)}}{{T}_{s(1)}{G}_{1}{G}_{2}{G}_{3}\cdots {G}_{n-1}}}{\text{,}}}$

(16)

where ${\displaystyle {T}_{s(n)}}$ represents the temperature driving stage ${\displaystyle {n}}$ (i.e. the accumulated noise of all stages prior to stage ${\displaystyle {n}}$).

This formula fails when the ${\displaystyle {F}_{n}}$ refer to IEEE noise factors.

Because of the need for two cascade noise-factor formulas and the risk of misapplication, when doing a cascaded signal chain SNR analysis the author recommends always using the risk-free and completely general “Friis formula for noise temperature” given above in equation 14. In other words, always follow these three steps:

(1) convert ${\displaystyle F_{std}}$ numbers to a ${\displaystyle T_{e}}$ using equation 10, or ${\displaystyle F_{op}}$ numbers to a ${\displaystyle T_{e}}$ using equation 6 (which requires knowledge of ${\displaystyle T_{s}}$), then

(2) create an equivalent input noise temperature ${\displaystyle T_{e}}$ for the cascaded chain using equation 14, and finally

(3) convert the cascaded chain's ${\displaystyle T_{e}}$ into either an ${\displaystyle F_{op}}$ using equation 5 if an SNR reduction metric desired, or an ${\displaystyle F_{std}}$ using equation 9 if a non-linear sensitivity indicator is desired.

Following these three steps guarantees producing correct results for both Friis and IEEE/IEC noise-figure numbers. Do not be tempted to use special cases or non-general formulas. To reduce the risk of errors, it is much safer to never depend on special cases. Instead, simply always use the same reliable and generic three steps listed above. And never use ${\displaystyle F_{std}}$ or ${\displaystyle NF_{std}}$ as if they refer to or approximate an SNR reduction, because they don't.

Effective Noise Temperature ${\displaystyle {T}_{e}}$ For An Attenuator Or Cable

An impedance matched attenuator stage, like a transmission line or resistive network, with a physical temperature ${\displaystyle {T}_{a}}$ (a for attenuator) and a gain of ${\displaystyle G={P}_{out}/{P}_{in}}$ (ratio of output power to input power), has an effective input noise temperature of ,

${\displaystyle {T}_{e}=\left({\frac {1}{G}}-1\right){T}_{a}{\text{.}}}$

(17)

Special Cases

Suppose the resistive loss elements (e.g. resistors in an attenuator, or the conductors in a transmission line or inductor) have a physical temperature ${\displaystyle {T}_{a}}$ equal to the source temperature ${\displaystyle {T}_{s}}$ driving the attenuating block. Under this condition we have,

${\displaystyle {F}_{op}=\left.{\frac {1}{G}}\right|_{{T}_{a}={T}_{s}}}$

(18)

In this special case, the noise coming out is unchanged, while the signal power is reduced. As such, the SNR loss is the same as the signal loss. While an interesting theoretical outcome, this special case rarely occurs in practice and should not be assumed―an example of which is illustrated in the § Example Usage section.

The same special case applied to the IEEE/IEC definition is

${\displaystyle {F}_{std}=\left.{\frac {1}{G}}\right|_{{T}_{a}=290\ {\text{K}}{\text{.}}}}$

(19)

While this case is more likely to be a reasonable approximation in room temperature settings, since the ${\displaystyle {290\ {\text{K}}}}$ "room temperature" IEEE/IEC standard is more likely to be close to the actual operating ${\displaystyle {T_{s}}}$ of low power attenuators and cables in that setting, it is still a special case which is unnecessary to use and easily avoided. In both cases, it is much safer to use equation 17 and follow the § rules.

Since many people learn or solidify their understanding better by way of example, we will evaluate a system with a series connected antenna, lossy cable, and receiver to serve this purpose. We will look at the SNR impact of the components on the system performance and what limits each component places on the system's performance. Suppose we have a room temperature ${\displaystyle (290\ {\text{K}})}$ cable with ${\displaystyle 0.4\ \mathrm {dB} }$ of loss. In this case, the cable's gain is ${\displaystyle G_{1}=10^{\frac {-0.4}{10}}=0.912}$. Applying equation (17) the cable has an effective input noise temperature of ${\displaystyle T_{1}=(1/G_{1}-1)\times 290\ {\text{K}}=0.096\times 290\ {\text{K}}=28\ {\text{K}}{\text{.}}}$ From equation (9) it would have an IEEE standard ${\displaystyle {NF}_{std}=10\ \log \left(1+{\frac {28\ {\text{K}}}{290\ {\text{K}}}}\right)=0.4\ \mathrm {dB} {\text{.}}}$

Next we will use the Friis formula for noise temperature (14) to look at combinations of components. Since the above ${\displaystyle 0.4\ \mathrm {dB} }$ loss cable is the first component in the chain, ${\displaystyle {T}_{1}=28\ {\text{K}}}$ and all the other noise contributions are amplified by the cable loss ${\displaystyle {\frac {1}{{G}_{1}}}{\text{,}}}$ or ~ ${\displaystyle 1.1}$ – i.e. relatively speaking, the noise from other components is effectively raised up about 10% in this example due to the loss in the cable.

Suppose this cable is in front of a receiver, and the receiver has an input effective noise temperature of ${\displaystyle {T}_{2}=10\ {\text{K}}{\text{,}}}$ then the overall input ${\displaystyle {T}_{e}}$ for the cable/receiver combination from equation (14) is

${\displaystyle T_{e}=T_{1}+{\frac {T_{2}}{G_{1}}}=28\ {\text{K}}+{\frac {10\ {\text{K}}}{0.912}}=39\ {\text{K}}}$

Suppose the small antenna in our system has an output noise temperature of ${\displaystyle {T}_{s}=2\ {\text{K}}{\text{,}}}$ and it connects to the previous 0.4 dB loss room temperature cable, and then to the previous ${\displaystyle {T}_{2}=10\ {\text{K}}}$ receiver. Since the system input ${\displaystyle {T}_{e}=38.94\ {\text{K}}{\text{,}}}$ the total SNR degradation from the system would be computed from equation (5) as,

${\displaystyle {F}_{op}=1+{\frac {{T}_{e}}{{T}_{s}}}=1+{\frac {38.94\ {\text{K}}}{2\ {\text{K}}}}=20.47}$ or

${\displaystyle NF_{op}=10\ \log \left(F_{op}\right)=13.11\ {\text{dB.}}}$

Without the ${\displaystyle 0.4\ \mathrm {dB} }$ loss cable, the SNR degradation from the ${\displaystyle {T}_{2}=10\ {\text{K}}}$ receiver alone would be reduced to,

${\displaystyle {F}_{op}=1+{\frac {{T}_{e}}{{T}_{s}}}=1+{\frac {10\ {\text{K}}}{2\ {\text{K}}}}=6}$ or

${\displaystyle NF_{op}=10{\text{ }}\log \left(F_{op}\right)=7.78{\text{ dB}}{\text{,}}}$

which is ${\displaystyle 13.11-7.78=5.33{\text{ dB}}}$ less degradation. Note that this ${\displaystyle 5.33{\text{ dB}}}$ is the SNR reduction caused by adding the cable to the above system, and that this ${\displaystyle 5.33{\text{ dB}}}$ SNR loss is different from the SNR loss across the cable alone, which, from the ${\displaystyle {T}_{1}=28\ {\text{K}}}$ cable, is,

${\displaystyle {F}_{op}=1+{\frac {{T}_{e}}{{T}_{s}}}=1+{\frac {28\ {\text{K}}}{2\ {\text{K}}}}=15}$

${\displaystyle NF_{op}=10\ \log \left({F}_{op}\right)=11.76{\text{ dB}}}$

The effective noise temperature at the cable output, ${\displaystyle T_{co}}$, whose input noise temperature was ${\displaystyle {T}_{1}=28\ {\text{K}}}$, is

${\displaystyle {T}_{co}=G_{1}\left({T}_{s}+{T}_{1}\right)=0.912\left(2\ {\text{K}}+28\ {\text{K}}\right)=27.34\ {\text{K}}}$

The additional SNR reduction caused by the ${\displaystyle {T}_{2}=10\ {\text{K}}}$ receiver is

${\displaystyle {F}_{op}=1+{\frac {{T}_{2}}{{T}_{sco}}}=1+{\frac {10\ {\text{K}}}{27.3\ {\text{K}}}}=1.366}$

${\displaystyle {NF}_{op}=10\ \log \left({F}_{op}\right)=1.35{\text{ dB}}}$

So the total SNR reduction from the cable ${\displaystyle (11.76{\text{ dB}})}$ and the receiver (${\displaystyle (1.35{\text{ dB}})}$ ) is

${\displaystyle 11.76{\text{ dB}}+1.35{\text{ dB}}=13.11{\text{ dB}}{\text{,}}}$

which matches the ${\displaystyle 13.11{\text{ dB}}}$ we initially calculated for the entire system.

Study of this example is useful and should give the reader the following takeaways:

1. The ${\displaystyle 0.4\ \mathrm {dB} }$ loss cable, with an ${\displaystyle {NF}_{std}=0.4\ {\text{dB}}{\text{,}}}$ actually loses ${\displaystyle NF_{op}=11.76{\text{ dB}}}$ of SNR between its input and its output in this example.
2. From (#1), If one thinks of ${\displaystyle {NF}_{std}}$ as an SNR metric, they would be gravely mistaken. ${\displaystyle {NF}_{std}}$ is off by ${\displaystyle 11.36\ {\text{dB}}}$, which is tremendously misleading. The definitions give significantly different results. As was stated in the overview, ${\displaystyle {NF}_{std}}$ is not an SNR metric nor is it an approximation to one.
3. In this particular system, the cable causes an extra ${\displaystyle 5.33\ \mathrm {dB} }$ of SNR loss relative to having no cable at all. If one worked hard to reduce the ${\displaystyle 0.4\ \mathrm {dB} }$ cable loss in this system (i.e. no receiver change), the best possible improvement that could be made in the SNR is ${\displaystyle 5.33\ \mathrm {dB} {\text{,}}}$ even though the SNR loss across the cable, in the system, is ${\displaystyle 11.76\ \mathrm {dB} {\text{.}}}$ In other words, the more one reduces the SNR loss in the cable, the more SNR loss there is in the receiver. In this example, only by improving both the receiver and the cable can the SNR be improved by more than ${\displaystyle 5.33\ \mathrm {dB} {\text{.}}}$
4. If one worked hard to improve the receiver in this system (i.e. with no cable change), the best possible improvement that could be made in the SNR is only ${\displaystyle 1.35\ \mathrm {dB} {\text{.}}}$ Only by reducing the cable loss would the way be opened for a receiver improvement to make more than ${\displaystyle 1.3\ \mathrm {dB} }$ of SNR improvement.
5. Only ${\displaystyle {NF}_{op}}$ provides accurate information regarding each component's impact to the system's SNR, and clear insight into what an investment in improving a particular component would have in improving the system's performance.

The study and characterization of antenna noise has a long and ongoing history. Techniques for measuring the noise parameters of antennas are described in reference . Antennas require special attention because (1) they are a transducer with different units on their input port (i.e. volts/m) versus output port/s (i.e. volts), (2) their gain is not fixed but changes with a signal's angle of arrival (AoA), (3) their output noise has up to six components that may or may not be included in any specification or reference, and (4) additional factors may or may not be included, like (a) polarization, which adds another dimension, causing the 2-port looking device to become a 3-port device with ports for two orthogonal polarizations, and (b) matching losses. The six components of noise associated with antennas are: (1) self generated noise, which is related to the antenna's efficiency and physical temperature, (2) far-field noise picked up by the antenna according to the antenna's gain at different angles and the environmental "brightness" level at those angles, (3) local near-field and conducted noise, such as the noise coupled from a cell-phone's display into its antenna by radiation and ground currents, (4) noise introduced by mutual coupling between ports on an array, since the noise going into one port (e.g. from a resistive termination or the noise from a receiver connected to the port) can affect the noise coming out of other ports, (5) noise generated by the matching network, which for phased arrays, may be a multi-port network and may introduce additional coupling between ports, and (6) noise generated by a physically built-in low noise amplifier (LNA), such that the "antenna's" output is the output of the LNA. Regarding the self generated noise, antennas close to the earth and especially monopoles with ground wires in or on the ground, the lossy ground is part of the antenna. The ground loss reduces the antenna's efficiency and contributes to its self-generated noise component.

Both Friis and IEEE/IEC noise figure definitions can be and are applied to an antenna. The complexities of the above factors, however, mean that both noise figure definitions can be based on a plethora of different cases regarding which noise components and factors are included.

As a result, the reader of an antenna noise figure specification must determine which "noise figure" definition is being used and what factors it includes from the context of its use. Authors need to make clear the same. An IEEE/IEC noise figure number that includes an LNA, for example, is significantly higher than that of the same antenna without the LNA. In this case, higher numbers simply mean a higher gain LNA has been used. Ideally, Friis noise figure numbers will be nearly equal with and without the LNA, indicating the LNA's input noise is low enough that the output SNR is limited by the SNR in the air, and not the LNA's noise.

The key to calculating an antenna's Friis noise figure is measuring the noise made by the antenna itself, which is done by measuring its radiation efficiency ${\displaystyle {(\eta _{r})}}$ and its physical temperature. If a net 1 watt was flowing into a perfectly efficient antenna, the total power radiated out, or in other words, the power integrated over the surface of a sphere containing the antenna, would also be 1 watt. But because an antenna is not constructed with perfect lossless conductors, dielectrics, and magnetic materials, the antenna's radiation efficiency is less than 100%. As a result (1) less than 1 watt is radiated, and (2) the antenna produces its own noise. The noise it produces itself is proportional to its efficiency and temperature.

Suppose ${\displaystyle T_{B}(\theta ,\phi )}$ represents the brightness of noise energy that is impinging on an antenna versus angle, where the energy matches the polarization of the antenna. By reciprocity, if that antenna had 100% efficiency and was perfectly matched, just like 1 watt in must result in 1 watt out when transmitting, when receiving energy at a particular frequency, and at that frequency ${\displaystyle D(\theta ,\phi )}$ is the antenna's far field directivity pattern, the noise temperature it produces at its output due to the far field radiation it collects is

${\displaystyle T_{a}={\frac {\int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }\ T_{B}(\theta ,\phi )D(\theta ,\phi )\sin \theta \ d\theta \ d\phi }{\int \limits _{0}^{2\pi }\int \limits _{0}^{\pi }D(\theta ,\phi )\sin \theta \ d\theta \ d\phi }}}$

(20)

Let the impedance matching efficiency from the antenna-load's impedance be ${\displaystyle \tau }$, where ${\displaystyle \tau =(1-|\Gamma |^{2})}$ and ${\displaystyle \Gamma }$ is the reflection coefficient. So ${\displaystyle \tau =1}$ for no reflection or no loss from matching, and ${\displaystyle \tau \rightarrow 0}$ for total reflection or complete loss from the matching. If the antenna's radiation efficiency is ${\displaystyle \eta _{r}{\text{,}}}$ matching efficiency is ${\displaystyle \tau {\text{,}}}$ and physical temperature is ${\displaystyle T_{p}{\text{,}}}$ then the noise temperature coming out of the antenna is

${\displaystyle T_{A}=\tau {\text{.}}}$

(21)

Here, the first term, ${\displaystyle \tau \eta _{r}T_{a}{\text{,}}}$ is the source noise, and the second term, ${\displaystyle \tau (1-\eta _{r})T_{p}{\text{,}}}$ is the noise added by the antenna.

For example, any antenna loaded with a perfect match, regardless of size, gain, gain pattern, and radiation efficiency, that is put into a shielded chamber, where the physical temperature of antenna and chamber are ${\displaystyle T_{p}}$ (i.e. matched), so ${\displaystyle T_{B}(\theta ,\phi )=T_{p}{\text{,}}}$ will have an output noise temperature ${\displaystyle T_{A}=T_{a}=T_{p}{\text{.}}}$

In receive mode, the input signal and noise sources are electromagnetic fields with a polarization and units of ${\displaystyle {\text{V}}/{\text{m}}}$ or ${\displaystyle {\text{W}}/{\text{m}}^{2}{\text{,}}}$ which are related by the impedance of the media, e.g. ~377 ohms for the impedance of free space. The output has units of ${\displaystyle {\text{V}}}$ or ${\displaystyle {\text{W,}}}$ which are related by the load impedance connected across the antenna's terminals, ${\displaystyle {Z_{L}}{\text{.}}}$ An antenna's antenna factor ${\displaystyle {AF(f,\theta ,\phi ,Z_{L})}}$ has units of ${\displaystyle 1/{\text{m}}}$ and relates the incoming ${\displaystyle E_{in}{\text{V}}/{\text{m}}}$ field, to the voltage ${\displaystyle {V}_{out}}$ on the antenna's output terminals. When the incoming field is at some frequency ${\displaystyle {\text{(}}f{\text{)}}}$, azimuth and elevation angle ${\displaystyle {\text{(}}\theta ,\phi {\text{),}}}$ and polarization matching the ${\displaystyle {AF}}$'s definition, and the antenna's output terminal is loaded with an impedance of ${\displaystyle Z_{L}}$ ohms, the input and output of the antenna are related as,

${\displaystyle {V}_{out}={\frac {E_{in}}{AF(f,\theta ,\phi ,Z_{L})}}{\text{ or }}{E}_{in}={V}_{out}{AF(f,\theta ,\phi ,Z_{L})}}$

(22)

Each term, ${\displaystyle V_{out}{\text{, }}AF{\text{, and }}{E}_{in}{\text{,}}}$ can be complex. In general, an antenna is a 3-port device for an arbitrarily polarized field, but in this case it is treated as a 2-port device where the polarization of the received field, ${\displaystyle {E}_{in}{\text{,}}}$ matches that of the ${\displaystyle {AF}}$ function, which is typically that of the antenna. ${\displaystyle AF}$ is inversely related to an antenna's effective length, ${\displaystyle {h}}$, where ${\displaystyle {AF(at{\text{ }}Z_{L}=\infty \Omega )=1/h}}$. But ${\displaystyle {AF}}$ is scaled to include the effect of the antenna's efficiency, impedance, and the load's impedance ${\displaystyle {(Z_{L})}}$. So ${\displaystyle {AF}}$ includes losses due to both efficiency and impedance match.

A full antenna characterization models the antenna with frequency dependent parameters that allow calculation of (1) an antenna's optimum load impedance ${\displaystyle Z_{L}{\text{,}}}$ (2) its efficiency and therefore its self generated noise, (3) its reflection coefficient at its output port (like an S22), (4) its angle dependent radar cross section (RCS) (like an S11), and (5) its angle dependent transfer function, ${\displaystyle {\frac {1}{AF}}}$ (like a receiving S21 and transmitting S12).

The parameters in this antenna model allow computation of its efficiency, matching efficiency, ${\displaystyle D(\theta ,\phi )}$, and ${\displaystyle {AF(f,\theta ,\phi ,Z_{L})}}$. These plus a brightness function ${\displaystyle T_{B}(\theta ,\phi )}$ for the environment allow computation of the source noise term and the added noise term in equation 21. The input noise temperature of a receiver attached to the antenna, ${\displaystyle T_{r}{\text{,}}}$ is required in order for an SNR analysis to determine what impact changing an antenna's efficiency, matching efficiency, and beam-shape will have, or what impact the receiver's input noise temperature will have on a system's performance. The antenna factor function allows translation between an effective noise voltage at the antenna output, and an effective ${\displaystyle {\text{V}}/{\text{m}}}$ noise field strength, allowing expression of a system's sensitivity in terms of a ${\displaystyle {\text{V}}/{\text{m}}}$ field strength.

Using the source noise and added noise terms from equation 21, the Friis noise factor for the antenna alone is

${\displaystyle F_{op}=1+{\frac {T_{p}(1-\eta _{r})}{T_{a}\eta _{r}}}}$

(23)

With electrically small antennas, the efficiency, ${\displaystyle \eta _{r}}$, can cause the system's ${\displaystyle NF_{op}}$ to blow up. Even though the matching efficiency ${\displaystyle \tau }$ disappears from the equation for the noise figure of the antenna alone, ${\displaystyle \tau }$ can be the dominant term when the antenna is connected to a receiver. When the antenna is connected to a receiver with an input noise temperature of ${\displaystyle T_{r}{\text{,}}}$ the Friis noise factor for the antenna and receiver combination is

${\displaystyle F_{op}=1+{\frac {\tau T_{p}(1-\eta _{r})+T_{r}}{\tau T_{a}\eta _{r}}}{\text{.}}}$

(24)

This equation shows that, unlike the antenna alone, the system's ${\displaystyle NF_{op}}$ noise figure blows up as ${\displaystyle \tau }$ goes toward zero. Particularly with electrically small antennas, both ${\displaystyle \tau }$ and ${\displaystyle \eta _{r}}$ can cause the system's ${\displaystyle NF_{op}}$ to blow up.

An antenna's noise figure specification is sometimes based on using equation 9 to express its output's effective noise temperature as an ${\displaystyle F_{std}}$ noise factor.

This usage can be confusing for several reasons. One is that the IEEE/IEC definition does not formally work since the IEEE/IEC specified ${\displaystyle 290\ {\text{K}}}$ source that drives the input has an output power with units of watts ${\displaystyle {\text{W,}}}$ which is not the ${\displaystyle {\text{W/m}}^{2}}$ required by the input of the antenna. Another is that other 1-port devices characterized by an IEEE/IEC noise figure, like a noise source, have an output that does not depend on their environment or an input, since they have none. Their characterization applies to the device alone. But in the case of an antenna, just the reverse; the characterization is still in-situ. It depends on the input―the specific ${\displaystyle T_{B}(\theta ,\phi )}$ noise environment the antenna is placed into and where the antenna beam is aimed. It also depends on the in-situ load impedance placed across the antenna's output terminals and the resulting matching efficiency.

In the case of an amplifier, ${\displaystyle NF_{std}}$ applies to an isolated amplifier while ${\displaystyle NF_{op}}$ applies to an in-situ amplifier. For antennas, both metrics are in-situ.

On all other 2-port devices, ${\displaystyle NF_{std}}$ expresses the input-referred noise temperature, which represents an absolute sensitivity. But for an antenna, ${\displaystyle NF_{std}}$ is output-referred. This difference is significant and leads to confusion regarding two ideas. The first idea is that the lower the noise figure the better, as lower indicates better sensitivity for receivers and amplifiers. But with an antenna, because it represents an output referred noise, the widely accepted idea that "lower is better" is not necessarily true. For example, a low matching efficiency hurts performance but produces a lower output noise temperature. Similarly, a low gain LNA within an antenna can produce lower output noise yet hurt performance versus the same antenna containing a higher gain LNA. The second idea is that ${\displaystyle NF_{std}}$ represents an absolute sensitivity metric, which is true for 2-port devices like amplifiers and receivers, but is not true for antennas.

In practice, these issues are ignored. It must be simply be understood that (1) the noise figure is not for an isolated antenna but for an in-situ antenna , (2) that the antenna is not being treated as a 2-port device, but is being treated as a 1-port device with only an output, and (3) that the "noise figure" represents neither a sensitivity nor an SNR reduction. Whatever noise an antenna picks up due to its environment and aiming, plus any self generated noise, plus noise from other things included in the "antenna" like matching networks and LNA, appears as some power across the load connected to its output. Measuring the output noise power across a system’s effective noise bandwidth ${\displaystyle B}$ allows this output noise to be expressed as an effective noise temperature ${\displaystyle {T}_{out}}$ such that ${\displaystyle k_{B}{T}_{out}B}$ produces the measured noise power. Isolating the noise generated within the antenna alone versus that from incoming fields as was done in the Friis formulation is not done. This ${\displaystyle {T}_{out}}$ is simply converted to an IEEE noise factor/figure with equation 9, the as-practiced IEEE/IEC standards' equation without the constraints.

Given an antenna’s ${\displaystyle {NF}_{std}{\text{,}}}$ a system SNR analysis process starts in the standard way (i.e. following the rules ), by converting the antenna’s ${\displaystyle {NF}_{std}}$ back to an effective noise temperature, which becomes the effective source temperature ${\displaystyle {T}_{s}}$ going into the receiving system connected to the "antenna" (which might include an amplifier). A cascaded chain SNR analysis finds an effective input noise temperature ${\displaystyle {T}_{e}}$ for the receiver using Friis's cascaded temperature formula 14.

SNR Reduction Due to Receiver: Using these ${\displaystyle {T}_{s}}$ and ${\displaystyle {T}_{e}}$ numbers in ${\displaystyle {NF}_{op}}$ formula 5 finds the SNR loss caused by the receiver's ${\displaystyle {T}_{e}}$, relative to the antenna output's ${\displaystyle {T}_{s}}$. This analysis does not isolate any SNR loss in the antenna itself, or provide insight as to how changing its match or efficiency might affect the system performance.

Sensitivity: A radio system's sensitivity is input referred and requires an effective input field strength ${\displaystyle E_{e}{\text{V/m}}}$. A 0 dB SNR sensitivity calculation requires an antenna factor ${\displaystyle AF(f,\theta ,\phi ,Z_{L})}$ (which may include gain stages), and an effective total noise voltage ${\displaystyle V_{n}{\text{,}}}$ where both are referenced to a common point in the signal chain. Assuming ${\displaystyle {T}_{s}}$ and ${\displaystyle {T}_{e}}$ were measured at a common reference point having an impedance of ${\displaystyle Z_{L}}$ ohms, ${\displaystyle V_{n}={\sqrt {Z_{L}\ k_{B}(T_{e}+T_{s})B}}{\text{.}}}$ Following from equation 22, the a signal's level (i.e. V/m field strength) required to come into the antenna to produce an output voltage of ${\displaystyle V_{n}{\text{,}}}$ (i.e. equal to the noise) at that common reference point, for any frequency and angle and load impedance, is simply ${\displaystyle E_{e}{\text{V/m}}=V_{n}\times AF(f,\theta ,\phi ,Z_{L}){\text{.}}}$ ${\displaystyle E_{e}}$ is the system's sensitivity versus frequency, angle, and load impedance.

The ITU radio noise report uses this approach to quantify atmospheric noise levels as both a volts/m field strength, and as an IEEE/IEC noise factor, based on an isotropic, 100% efficient, perfectly matched, Gain=1 receive antenna, which has an antenna factor of ${\displaystyle AF={\sqrt {\frac {4\pi \eta }{Z_{L}}}}{\frac {f}{c}}}$.

In 1942 Friis, working at Bell Labs in Holmdel NJ, invented the concept of an SNR reduction metric. Reference gives a more complete history of the development and use of noise-figure. Fundamentally, ${\displaystyle {NF}_{op}}$ is a function of two variables (two temperatures, ${\displaystyle {T}_{s}}$ and ${\displaystyle {T}_{e}}$) that answers the question, "When a block is used in a system with a specific incoming SNR, how many dB does SNR drop by between the input and output of that block?"

Below is a pictorial illustrating the derivation of Friis’s ${\displaystyle F_{op}}$ and SNR formula, which assumes perfect impedance matching on the input and output of the amplifier.

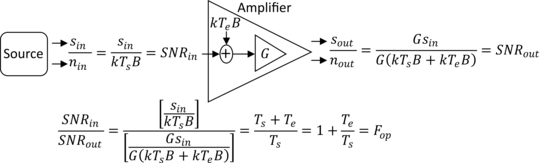
It is important to grasp that this equation does not allow one to set ${\displaystyle T_{s}}$ to a particular temperature, like ${\displaystyle 290\ {\text{K}}{\text{,}}}$ on one side of the equation (e.g. ${\displaystyle n_{in}}$ on the input side) and not also on the other side (e.g. ${\displaystyle n_{out}}$ on the output side). ${\displaystyle T_{s}}$ is buried within both the ${\displaystyle SNR_{in}}$ term and the ${\displaystyle SNR_{out}}$ term. In order for an ${\displaystyle {NF}_{op}=1\ {\text{dB}}}$ to mean that ${\displaystyle SNR_{out_{dB}}}$ is ${\displaystyle 1\ {\text{dB}}}$ worse than ideal (i.e. worse than the ${\displaystyle SNR_{in_{dB}}}$), both ${\displaystyle {n}_{in}}$ and ${\displaystyle {n}_{out}}$ must use the same ${\displaystyle {T}_{s}{\text{,}}}$ and ${\displaystyle {T}_{s}}$ must represent the actual source temperature. All the terms on both sides must stay consistent.

Friis’s ${\displaystyle f(T_{e},T_{s})}$ function in equation (3) allowed engineers, for the first time, to calculate the degradation that an arbitrary block had on the signal-to-noise ratio (SNR) of a signal passing through it. Friis's noise-figure ${\displaystyle {NF}_{op}}$ cannot be applied to an isolated receiver alone or an amplifier alone because the SNR degradation across it depends on what the amplifier or receiver is connected to—i.e. how noisy the source is. In order to compute an “SNR reduction”, one must have access to both ${\displaystyle {T}_{s}}$ and ${\displaystyle {T}_{e}{\text{.}}}$ From these two values, “noise-figure” ${\displaystyle {NF}_{op}}$ characterizes how much a block, as used in the system it is connected to, degrades the signal-to-noise ratio (SNR).

Formally Constrained But Unconstrained In Practice

While using specific source temperatures like ${\displaystyle 290\ {\text{K}}}$, or ${\displaystyle 293\ {\text{K}}}$, or ${\displaystyle 300\ {\text{K}}}$ was commonly done from the early days, on June 11, 1959, the IRE published a standard for measuring and marking devices, like a amplifier, even though the device was not connected to, or being used in, a system where ${\displaystyle {T}_{s}}$ could be factored in. On January 1, 1963, the AIEE and the IRE merged to form the Institute of Electrical and Electronics Engineers (IEEE), and this second definition for “noise-figure” remains an IEEE standard. Reference is the originating document for the IEEE’s noise-figure definition and has remained the same since then. The IEC standard is essentially identical but simply states that the temperature is "around ${\displaystyle 290\ {\text{K}}}$".

The IEEE's formal definition is

${\displaystyle F_{std}=1+{\frac {T_{e}}{290\ {\text{K}}}}|_{T_{s}=290\ {\text{K}}}}$

(26)

This formula is a conditional or constrained formula. It is a formula that is always "wrong/undefined" except for the singularity (when ${\displaystyle {T}_{s}=290\ {\text{K}}}$) where it is defined. In this case, "wrong/undefined" means that the value coming out of the formula does not equal or mean an SNR reduction like Friis's noise-figure, and formally, no value should actually come out of the formula because the formula is undefined except at that singularity.

This constrained definition can be confusing because as it is commonly used (i.e. in practice), the strict and formal constraint is completely ignored. What is vital for the reader to understand, is that when the vertical bar constraint is removed, the remaining generic-looking function no longer generically relates to, equals, or means an SNR reduction. As such, an IEEE/IEC noise figure cannot be used in equations 3 through 7. They are incompatible. To highlight this point by way of example, suppose a constrained formula relating the temperature in Fahrenheit and Celsius was given as

${\displaystyle T_{F}=T_{C}|_{T_{C}=-40^{\circ }}{\text{.}}}$

If the constraint is removed or ignored, the remaining equation is simply wrong, the slope is wrong, and any derivation based on it will be wrong.

Unfortunately, the originating text in implies that the unconstrained equation is an "approximation", when ${\displaystyle T_{s}\approxeq 290\ {\text{K}}{\text{,}}}$ where the approximation is to another different but identically named term (i.e. Friis's noise factor) that (1) is broadly understood (i.e. the SNR reduction metric from Friis that had enjoyed common use for 15 years), (2) is precisely defined (the exact SNR reduction across two ports of a two-port device), (3) is unique (not duplicated or represented by a standard or any other term), and (4) is never defined or described within the text of the originating document, or the IEEE standard, or the Federal standard, or the IEC standard. Two juxtaposed facts further contribute to the confusion. The first is that the formal definitional formula has a mathematically strict constraint, where the constraint means the term is only defined and the formula only applies to the case where (1) it refers to a 2-port network with an input and an output, and (2) when that input is connected to a source whose noise temperature ${\displaystyle T_{s}}$ is known to be exactly ${\displaystyle 290\ {\text{K}}{\text{.}}}$ Only if both restrictions are true (i.e. ${\displaystyle T_{s}\equiv 290\ {\text{K}}{\text{,}}}$ and the block has an input and an output), do the meanings of the IEEE and Friis definitions match. Juxtaposed is that while both of the above two restrictions are at the core of the IEEE/IEC standard's formal definition, in practice, both restrictions are removed and ignored. In practice, the IEEE's definition is the unconstrained single-parameter function given in equation 9 in the overview.

Approximation?―No

If the constraint is almost met, one might assert that formula 9 may be used to find an "approximate" SNR reduction value. For example, as long as the actual operating source temperature ${\displaystyle T_{s}}$ is within +/- 10% of the IEEE's ${\displaystyle 290\ {\text{K}}}$ number, ${\displaystyle F_{std}}$ will not have more than a +/- 10% error relative to the actual Friis noise factor. But the notion that formula 9 can be applied arbitrarily as an approximation (i.e. without regard for the source temperature or if 2 ports even exist) completely misses the fact that removal of the constraint in equation 26 completely changes the fundamental meaning of the formula. In practice, ${\displaystyle F_{std}}$ numbers are produced for:

(1) 1-port devices where ${\displaystyle T_{s}}$ does not exist and where the concept of an "SNR reduction between an input and output" does not apply or make sense, and

(2) 2-port devices without regard to ${\displaystyle {T}_{s}}$―where ${\displaystyle {T}_{s}}$ can be truly anything. It does not need to be close to ${\displaystyle 290\ {\text{K}}}$.

Consider the two cases, ignore or obey the constraints. In the first case where the formal constraints are ignored, the above two practices are so contrary to the constraints, that the IEEE standard's definition cannot be called an approximation or used as one. On the other hand, if the formal constraint is applied, then the IEEE standard's definition is exactly the same as the Friis definition. So again, it is not an approximation. In the end, in neither case is it an approximation.

Simply Not-Equal

As a result of the above two practices, ${\displaystyle NF_{std}}$ numbers cannot be substituted into Friis's operational formulas. In other words, as stated in the overview in equations 11, 12, and 13

${\displaystyle {NF}_{std}\neq {SNR}_{{in}_{dB}}-{SNR}_{{out}_{dB}}{\text{, and}}}$

${\displaystyle F_{std}\neq {\frac {{SNR}_{in}}{{SNR}_{out}}}{\text{.}}}$

General Definition

Regarding a simple general definitional statement, one might say that an amplifier's IEEE noise-figure is what Friis's noise-figure would be if that amplifier was connected to a system that had a source temperature of ${\displaystyle 290\ {\text{K}}{\text{.}}}$ While that statement is true, it fails to address 1-port networks. Also, it is not a direct statement about what the IEEE noise figure is, or what it means. Instead, it is a conditional statement about what it could mean if ${\displaystyle \ldots }$, which is not a general definition. Such a statement is simply a special case, constraint driven assertion.

Fortunately, there is a very simple general definition that is not hard to understand. The general definition for ${\displaystyle F_{std}}$, as defined in equation 9 is simply:

${\displaystyle F_{std}}$ is a non-linear monotonic transformation of an effective noise temperature at a port.

Or in other words,

${\displaystyle F_{std}}$ is a proxy for a noise temperature at a port.

The first page (page 61) of reference says,

“The noise factor, at a specified input frequency, is defined as the ratio of 1) the total noise power per unit bandwidth at a corresponding output frequency available at the output port when the noise temperature of the input termination is standard (${\displaystyle 290\ {\text{K}}}$ ) to 2) that portion of 1) engendered at the input frequency by the input termination.”

The use of the terms “output frequency” and “input frequency” are there to allow heterodyne systems, or in other words, blocks that use frequency conversion stages like mixers. What matters is that there is output noise power over some noise bandwidth ${\displaystyle B}$, there is source noise power coming in over the same noise bandwidth ${\displaystyle B}$, and the bandwidth does not cover the image-frequency band, but only the desired "corresponding" or principle frequency band. In this case, the matching noise bandwidths cancel in the ${\displaystyle SNR_{in}/SNR_{out}}$ ratio.

The “noise temperature of the input termination” is the source noise ${\displaystyle {T}_{s}}$ applied to (or going into) the input, and is defined, by the "when" clause, to be ${\displaystyle {T}_{s}\equiv 290\ {\text{K}}{\text{.}}}$ There is no variable ${\displaystyle T_{ref}}$ or ${\displaystyle T_{0}}$ in the IEEE text above, just a fixed "standard temperature", ${\displaystyle 290\ {\text{K}}}$. This "when" clause, this "standard temperature", is the constraint that is the essence of the IEEE standard. This ${\displaystyle 290\ {\text{K}}}$ "standard temperature" is what makes the IEEE and Friis definitions different.

Assuming a block has a gain of ${\displaystyle G{\text{,}}}$ and an effective input noise temperature of ${\displaystyle {T}_{e}{\text{,}}}$ the “total noise power per unit bandwidth…available at the output port” is

${\displaystyle \left.G\left(k_{B}{T}_{s}+k_{B}{T}_{e}\right)=G\ \left(k_{B}290\ {\text{K}}+k_{B}{T}_{e}\right)\right|_{T_{s}=290\ {\text{K}}}}$

(27)

The IEEE noise-factor is the ratio of “1)…” (the above equation (27)) to the “2)…” clause part, which is,

${\displaystyle F_{std}=\left.{\frac {G\left(k_{B}\ 290\ {\text{K}}+k_{B}{T}_{e}\right)}{G\ k_{B}\ 290\ {\text{K}}}}\right|_{T_{s}=290\ {\text{K}}}=\left.{\frac {{T}_{e}+290\ {\text{K}}}{290\ {\text{K}}}}\right|_{T_{s}=290\ {\text{K}}}=1+\left.{\frac {{T}_{e}}{290\ {\text{K}}}}\right|_{T_{s}=290\ {\text{K}}}}$

(28)

and is the same as equation 9 given in the overview.

The text in , immediately following the definition captured mathematically in equation 28 states,

“The standard noise temperature ${\displaystyle 290\ {\text{K}}}$ approximates the actual noise temperature of most input terminations."

This text has been misinterpreted to say that the unconstrained formula 9 approximates the constrained formula 28. But that is not what it says. The statement is saying that, to the degree ${\displaystyle 290\ {\text{K}}}$ approximates the actual ${\displaystyle T_{s}}$, the result from the constrained formula, ${\displaystyle {F}_{std}}$, "approximates" the Friis result ${\displaystyle {F}_{op}}$. But no conditions to limit the inaccuracy of the approximation are given. The misinterpreted "approximation" idea has been so misconstrued as to suggest ${\displaystyle F_{op}=F_{std}}$ and that operative formulas need no vertical bar restriction at all, making the defining equations simply

${\displaystyle {F}_{std}={h(T}_{e})=1+{\frac {{T}_{e}}{290\ {\text{K}}}}{\text{ and,}}}$ ${\displaystyle {T}_{e}=\left({F}_{std}-1\right)290\ {\text{K}},}$

as was stated in equations (9) and (10) in the overview section. As a result of loosing the constraint in its formal definition, these common usage formulas lose their connection to an SNR reduction and do not equal or mean an SNR reduction. They simply transform a temperature to a nonlinear space.

As practiced, for most two port devices (though not necessarily antennas), ${\displaystyle F_{std}}$ is the ratio of (1) the output noise power of a port on a device to (2) the portion thereof attributable to noise from an input termination whose noise temperature is exactly ${\displaystyle 290\ {\text{K}}{\text{.}}}$ For one-port devices ${\displaystyle F_{std}}$ is the ratio of (1) the output noise power of a port on a device to (2) that portion of 1) endangered by a fictitious "input" termination whose "gain" toward the output is 1, and whose noise temperature is exactly ${\displaystyle 290\ {\text{K}}{\text{.}}}$

Yes—the difference matters three ways. Reason "A", the difference matters because the values themselves can be vastly different and lead to extreme errors. Reason "B", the difference matters because the two formulas mean completely different things—one relates to a noise-power at a port, the other relates to a ratio of SNRs between two ports. Reason "C", the difference matters because erroneous derivative formulas will come from starting with an invalid formula (i.e. a constrained formula that becomes invalid because the constraint is removed).

Regarding Reason "A" – Vastly Different Values

In low noise applications like satellite communications, radio astronomy, and many applications using tiny “active antennas” where the tiny antenna puts out very little energy, the antenna noise temperatures can be less than ${\displaystyle 10\ {\text{K}}{\text{.}}}$ In this case, a ${\displaystyle 0.1\ {\text{dB}}}$ change in the IEEE noise figure ${\displaystyle (NF_{std})}$ can result in over ${\displaystyle 10\ {\text{dB}}}$ of change in ${\displaystyle {\text{SNR}}_{\text{dB}}{\text{.}}}$ So at source temperatures substantially below ${\displaystyle 290\ {\text{K}}}$ the two terms are far from being "approximately equal".

Huge discrepancies are not just a low temperature issue. The ITU radio noise report documents atmospheric and man-made noise. In the HF band (3-30 MHz) and below. According Figure 2 of this document, amateur radio antennas have noise temperatures in the 1 million to 1 trillion Kelvins range. Amateur radio operators have asked questions like, "why is my S-meter S-5 all the time". An S-5 power level is ${\displaystyle -97\ {\text{dBm}}}$, which on a 2.5 kHz bandwidth SSB receiver is an IEEE noise figure of ${\displaystyle 43\ {\text{dB}}}$. A ${\displaystyle 43\ {\text{dB}}}$ ${\displaystyle {NF}_{std}}$ is a noise temperature of 5.8 million Kelvins, which is 20,000 times higher than ${\displaystyle 290\ {\text{K}}}$. In this case, using a ${\displaystyle 10\ {\text{dB}}}$ IEEE noise figure ${\displaystyle {NF}_{std}}$ radio typical of today results in an ${\displaystyle {\text{SNR}}_{\text{dB}}}$ loss ${\displaystyle ({\text{i.e. }}{NF}_{op})}$ of just ${\displaystyle 0.002\ {\text{dB}}}$. Change that radio's ${\displaystyle {NF}_{std}}$ by ${\displaystyle 10\ {\text{dB}}}$, i.e. to ${\displaystyle 20\ {\text{dB}}}$, and its ${\displaystyle {\text{SNR}}_{\text{dB}}}$ loss budges ever so slightly to ${\displaystyle 0.02\ {\text{dB.}}}$ Clearly, (1) ${\displaystyle {NF}_{std}}$ does not indicate the ${\displaystyle {\text{SNR}}_{\text{dB}}}$ loss, and (2) the ${\displaystyle 10\ {\text{dB}}}$ change in ${\displaystyle {NF}_{std}}$ does not indicate a ${\displaystyle 10\ {\text{dB}}}$ change in ${\displaystyle {\text{SNR}}_{\text{dB}}}$. Its value is wrong and its slope is wrong. At source temperatures substantially above ${\displaystyle 290\ {\text{K}}}$ the two terms can be far from being "approximately equal".